안녕하세요. 지난 포스팅의 미적분학 - 로그함수 미분에서는 로그함수의 미분법과 로그함수를 포함한 다양한 합성함수의 미분법에 대해서 알아보았습니다. 오늘은 미분을 응용한 수치적 계산법인 선형근사법(Linear Approximation)에 대해서 설명드리도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
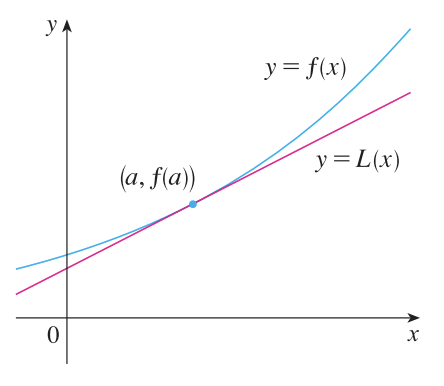
위 그림을 먼저 보시면 어느정도 이해가 가실겁니다. $x = a$에서 $f(x)$의 접선이 $L(x)$라고 할 때, $x = a$ 근처에서는 $y = L(x) = f(a) + f^{'}(x)(x - a)$와 $f(x)$가 별 차이가 나지 않는 다는 것을 볼 수 있습니다. 하지만, 멀어질수록 그 차이는 벌어지겠죠. 이러한 정보를 활용해서 $f(1)$에서의 값을 알고 있을 때, $f(1.0001)$과 같은 더 미세한 값을 근사하여 얻을 수도 있습니다. 이 관계를 수식으로 나타내면 아래와 같습니다.
$$f(x) \approx f(a) + f^{'}(a)(x - a)$$
예제1. $f(x) = \sqrt{x + 3}$일 때, $x = 1$에서의 접선을 찾고 $\sqrt{3.98}$을 유추하라.
$y = L(x) = f(1) + f^{'}(x)(x - 1)$이기 때문에 $f^{'}(x)$부터 구한다. 제곱근함수의 미분은 아래의 링크를 참조하라.
미적분학 - 다항함수와 지수함수의 미분
안녕하세요. 지난 포스팅의 미적분학 - 함수 미분에서는 기존의 미분을 구하는 법을 확장하여 일반적인 함수의 미분을 구하는 방법에 대해서 알아보았습니다. 하지만 항상 정의를 사용하여 미
everyday-image-processing.tistory.com
$$f^{'}(x) = \frac{1}{2\sqrt{x + 3}}$$
따라서, $f(x)$의 $x = 1$에서의 접선은 아래와 같다.
$$y = L(x) = 2 + \frac{1}{4}(x - 1)$$
선형근사식 $f(x) = \sqrt{x + 3} \approx 2 + \frac{1}{4}(x - 1)$이기 때문에 $x = 0.98$이라고 하면 $f(0.98) = \sqrt{3.98} \approx 1.995$이다.
연습문제1. 주어진 함수와 점에서의 선형근사식을 구하여라.
(a). $f(x) = x^{4} + 3x^{2}, a = -1$
(b). $f(x) = \ln(x), a = 1$
(c). $f(x) = \cos(x), a = \frac{\pi}{2}$
(d). $f(x) = x^{\frac{3}{4}}, a = 16$
(a). $f(x) = x^{4} + 3x^{2}, a = -1$
먼저, 주어진 함수의 도함수를 구한다.
$$f^{'}(x) = 4x^{3} + 6x$$
따라서, $a = -1$에서의 접선의 기울기는 $f(-1) = -4 + 6 = 2$이다. 따라서, 선형근사식은 아래와 같다.
$$L(x) = 2(x + 1) + 2 = 2x + 3$$
(b). $f(x) = \ln(x), a = 1$
먼저, 주어진 함수의 도함수를 구한다.
$$f^{'}(x) = \frac{1}{x}$$
따라서, $a = 1$에서의 접선의 기울기는 $f(1) = 1$이다. 따라서, 선형근사식은 아래와 같다.
$$L(x) = (x - 1) + 0 = x$$
(c). $f(x) = \cos(x), a = \frac{\pi}{2}$
먼저, 주어진 함수의 도함수를 구한다.
$$f^{'}(x) = -\sin(x)$$
따라서, $a = \frac{\pi}{2}$에서의 접선의 기울기는 $f(\frac{\pi}{2}) = -1$이다. 따라서, 선형근사식은 아래와 같다.
$$L(x) = -(x - \frac{\pi}{2}) + 0 = -x + \frac{\pi}{2}$$
(d). $f(x) = x^{\frac{3}{4}}, a = 16$
먼저, 주어진 함수의 도함수를 구한다.
$$f^{'}(x) = \frac{3}{4} x^{-\frac{1}{4}}$$
따라서, $a = 16$에서의 접선의 기울기는 $f(16) = \frac{3}{4} \cdot \frac{1}{2} = \frac{3}{8}$이다. 따라서, 선형근사식은 아래와 같다.
$$L(x) = \frac{3}{8}(x - 16) + 8 = \frac{3}{8}x + 2$$
연습문제2. 주어진 함수들의 도함수를 구하여라.
(a). $y = x^{2}\sin(2x)$
(b). $y = \frac{s}{1 + 2s}$
(c). $y = \frac{u + 1}{u - 1}$
(d). $y = e^{\tan(\pi x)}$
(a). $y = x^{2}\sin(2x)$
$$y^{'} = 2x\sin(2x) + 2x^{2}\cos(2x)$$
(b). $y = \frac{s}{1 + 2s}$
$$y^{'} = \frac{(1 + 2s) - 2s}{(1 + 2s)^{2}} = \frac{1}{(1 + 2s)^{2}}$$
(c). $y = \frac{u + 1}{u - 1}$
$$y^{'} = \frac{(u - 1) - (u + 1)}{(u - 1)^{2}} = -\frac{2}{(u - 1)^{2}}$$
(d). $y = e^{\tan(\pi x)}$
$$y^{'} = \pi \sec^{2}(\pi x) e^{\tan(\pi x)}$$
연습문제3. 주어진 함수들의 도함수를 구하여라.
(a). $y = \ln \sqrt{1 + t^{2}}$
(b). $y = e^{-u} \cos(u)$
(c). $y = (1 + r^{3})^{-2}$
(d). $y = \sqrt{1 + \ln(z)}$
(a). $y = \ln \sqrt{1 + t^{2}}$
$$y^{'} = \frac{2t}{1 + t^{2}}$$
(b). $y = e^{-u} \cos(u)$
$$y^{'} = -e^{-u}\cos(u) - e^{-u}\sin(u) = -e^{-u} (\sin(u) + \cos(u))$$
(c). $y = (1 + r^{3})^{-2}$
$$y^{'} = -6r^{2}(1 + r^{3})^{-3}$$
(d). $y = \sqrt{1 + \ln(z)}$
$$y^{'} = \frac{1}{2z\sqrt{1 + \ln(z)}}$$
연습문제4. 주어진 함수들과 점, 그리고 $dx$가 주어졌을 때 $dy$를 구하여라.
(a). $y = e^{\frac{x}{10}}, x = 0, dx = 0.1$
(b). $y = \frac{1}{x + 1}, x = 1, dx = -0.01$
(c). $y = \tan(x), x = \frac{\pi}{4}, dx = -0.1$
(a). $y = e^{\frac{x}{10}}, x = 0, dx = 0.1$
먼저, 주어진 함수의 도함수를 구한다.
$$\frac{dy}{dx} = \frac{1}{10}e^{\frac{x}{10}} \rightarrow dy = \frac{1}{10} e^{\frac{x}{10}} dx$$
이제 주어진 점과 $dx$를 대입하여 $dy$를 구한다.
$$dy = \frac{1}{10} e^{0} 0.1 = 0.01$$
(b). $y = \frac{1}{x + 1}, x = 1, dx = -0.01$
먼저, 주어진 함수의 도함수를 구한다.
$$\frac{dy}{dx} = -\frac{1}{(x + 1)^{2}} \rightarrow dy = -\frac{1}{(x + 1)^{2}} dx$$
이제 주어진 점과 $dx$를 대입하여 $dy$를 구한다.
$$dy = -\frac{1}{4} \cdot (-\0.01) = 0.0025$$
(c). $y = \tan(x), x = \frac{\pi}{4}, dx = -0.1$
먼저, 주어진 함수의 도함수를 구한다.
$$\frac{dy}{dx} = \sec^{2}(x) \rightarrow dy = \sec^{2}(x) dx$$
이제 주어진 점과 $dx$를 대입하여 $dy$를 구한다.
$$dy = 2 \cdot (-0.1) = -0.2$$
연습문제5. 주어진 숫자들의 근삿값을 구하여라.
(a). $(2.001)^{5}$
(b). $e^{-0.015}$
(c). $(8.06)^{\frac{2}{3}}$
(d). $\frac{1}{1002}$
(a). $(2.001)^{5}$
$f(x) = x^{5}$라고 할 때 $x = 2$에서 선형근사식 $L(x)$을 구한다. 이를 위해 함수 $f$의 도함수를 구하면 $f^{'}(x) = 5x^{4}$이므로 $x = 2$에서의 접선의 기울기는 $m = 80$이다. 따라서, 선형근사식은 $L(x) = 80(x - 2) + 32$이다.
$$f(2.001) \approx L(2.001) = 80(2.001 - 2) + 32 = 32.08$$
(b). $e^{-0.015}$
$f(x) = e^{x}$라고 할 때 $x = 0$에서 선형근사식 $L(x)$을 구한다. 이를 위해 함수 $f$의 도함수를 구하면 $f^{'}(x) = e^{x}$이므로 $x = 0$에서의 접선의 기울기는 $m = 1$이다. 따라서, 선형근사식은 $L(x) = (x - 0) + 1 = x + 1$이다.
$$f(-0.015) \approx L(-0.015) = -0.015 + 1 = 0.985$$
(c). $(8.06)^{\frac{2}{3}}$
먼저, $y = x^{\frac{2}{3}}$이라고 할 때, 주어진 함수의 도함수를 구하면 $\frac{dy}{dx} = \frac{2}{3}x^{-\frac{1}{3}}$이다. 이때, $dy = \frac{2}{3} x^{-\frac{1}{3}} dx$라고 쓰고 $x = 8$ 그리고 $dx = 0.06$이라고 한 뒤 $dy$를 구하면 된다.
$$dy = \frac{2}{3} \cdot \frac{1}{2} \cdot 0.06 = 0.02$$
따라서, $(8.06)^{\frac{2}{3}} \approx 8^{\frac{2}{3}} + 0.02 = 4.02$이다.
(d). $\frac{1}{1002}$
먼저, $y = \frac{1}{x}$이라고 할 때, 주어진 함수의 도함수를 구하면 $\frac{dy}{dx} = -\frac{1}{x^{2}}$이다. 이때, $dy = -\frac{1}{x^{2}} dx$라고 쓰고 $x = \frac{1}{1000}$ 그리고 $dx = 2$이라고 한 뒤 $dy$를 구하면 된다.
$$dy = -\frac{1}{1000^{2}} \cdot 4 = -\frac{4}{1000^{2}}$$
따라서, $\frac{1}{1002} \approx \frac{1}{1000} - \frac{4}{1000^{2}} = 0.000996$이다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.09.18 : 전체적인 스타일 수정
22.09.18 : 연습문제1-5 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 평균값 정리 (Mean Value Theorem; MVT) (0) | 2021.12.18 |
|---|---|
| 미적분학 - 최대값과 최소값 (0) | 2021.12.06 |
| 미적분학 - 로그함수 미분 (0) | 2021.11.23 |
| 미적분학 - 음함수의 미분 (0) | 2021.11.11 |
| 미적분학 - 연쇄 법칙 (0) | 2021.11.09 |
