안녕하세요. 지난 포스팅의 미적분학 - 최대값과 최소값에서는 전역최대 및 전역최소의 정의, 그리고 지역최대 및 지역최소의 정의, 마지막으로 임계값에 대해서 알아보았습니다. 그리고 이와 관련된 다양한 정리들(극값이론;Extreme Value Theorem, 페르마 정리;Fermat's Theorem)도 보았습니다. 오늘은 이어서 굉장히 중요하게 쓰이는 평균값 정리(Mean Value Theorem;MVT)에 대해서 알아보겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
하지만, 평균값 정리를 유도하기 전에 저희가 먼저 알아봐야 할 정리는 롤의 정리(Rolle's Theorem)입니다. 정리의 정확한 statement는 아래의 링크를 참조바랍니다.
Rolle's theorem - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search On stationary points between two equal values of a real differentiable function In calculus, Rolle's theorem or Rolle's lemma essentially states that any real-valued differentiable fun
en.wikipedia.org
정리1. 롤의 정리 (Rolle's Theorem)
함수 $f$가 아래의 3가지 조건을 만족한다고 가정하자.
1. 함수 $f$는 닫힌 구간 $[a, b]$에서 연속이다.
2. 함수 $f$는 열린 구간 $(a, b)$에서 미분가능하다.
3. $f(a) = f(b)$
위의 3가지 조건을 만족하는 함수 $f$는 열린 구간 $(a, b)$내에서 $f^{'}(c) = 0$을 만족하는 $c \in (a, b)$가 존재한다.
설명
롤의 정리는 아래의 몇 가지 함수의 예시들을 보시면 쉽게 이해하실 수 있습니다.
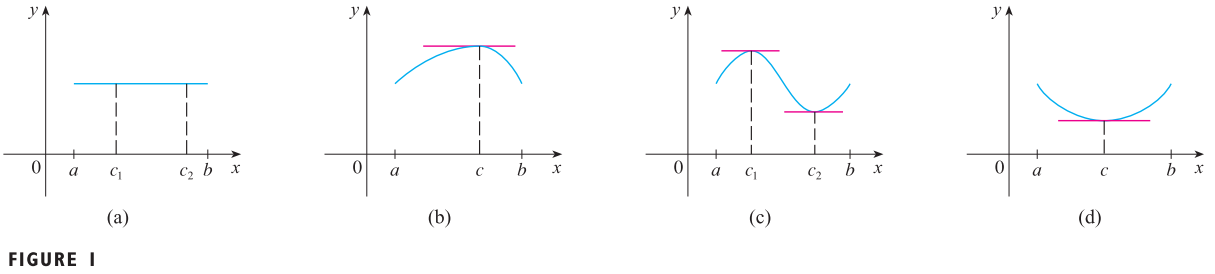
- 그림(a)는 모든 구간에서 상수함수입니다. 이때, 조건1, 2, 3 역시 만족하게 되죠. 또한 모든 구간에서 미분하면 0이기 때문에 $f^{'}(c) = 0$을 만족하는 $c$를 쉽게 찾을 수 있습니다.
- 그림(b)는 모든 함수값 $f(x)$가 항상 $f(a)$보다 큰 경우입니다. 그림을 보면 조건1, 2, 3 모두 만족한다는 것을 알 수 있습니다. 이 경우에는 결국에 증가했다가 다시 감소해야 $f(a) = f(b)$의 조건을 만족하게 만들 수 있습니다. 따라서 $f^{'}(x) > 0$에서 $f^{'}(x) < 0$이 되는 지점이 있기 때문에 $f^{'}(c) = 0$을 만족하는 $c$를 찾을 수 있습니다.
- 그림(c)는 몇몇 함수값 $f(x)$가 $f(a)$보다 작은 경우입니다. 이 경우에도 그림(b)와 마찬가지로 결국에는 함수의 증감이 바뀌는 지점이 있기 때문에 $f^{'}(c) = 0$을 만족하는 $c$를 찾을 수 있습니다.
- 그림(d)는 모든 함수값 $f(x)$가 $f(a)$보다 큰 경우입니다. 이 경우에도 그림(b)와 마찬가지로 결국에는 함수의 증감이 바뀌는 지점이 있기 때문에 $f^{'}(c) = 0$을 만족하는 $c$를 찾을 수 있습니다.
롤의 정리를 이해하셨다면 드디어 평균값 정리로 넘어갈 수 있습니다. 평균값 정리는 롤의 정리에서 조건을 약화시킨 일반화된 정리라고 보시면 될 거 같습니다. 정리의 정확한 statement는 아래의 링크를 참조바랍니다. 본 정리의 증명은 생략하도록 하겠습니다.
Mean value theorem - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search On the existence of a tangent to an arc parallel to the line through its endpoints In mathematics, the mean value theorem states, roughly, that for a given planar arc between two endpo
en.wikipedia.org
정리2. 평균값 정리(Mean Value Theorem; MVT)
함수 $f$가 아래의 2가지 조건을 만족한다고 가정하자.
1. 함수 $f$는 닫힌 구간 $[a, b]$에서 연속이다.
2. 함수 $f$는 열린 구간 $(a, b)$에서 미분가능하다.
위의 2가지 조건을 만족하는 함수 $f$는 열린 구간 $(a, b)$내에서 $f^{'}(c) = \frac{f(b) - f(a)}{b - a}$을 만족하는 $c \in (a, b)$가 존재한다.
증명
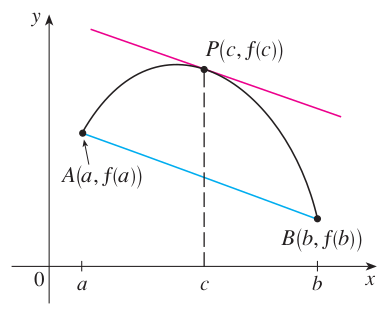
저희는 롤의 정리를 활용해서 평균값 정리를 증명할 수 있습니다. 따라서, 롤의 정리를 활용하기 위해 새로운 함수 $h$를 정의하도록 하겠습니다. 함수 $h$는 위 그림에서 보이는 함수 $f$와 할선 $AB$의 차이라고 정의하도록 하겠습니다. 이를 위해서는 할선 $AB$를 방정식의 형태로 써주어야겠죠? 여기서 할선 $AB$는 단순히 직선이기 때문에 아래와 같이 쓸 수 있습니다.
$$y - f(a) = \frac{f(b) - f(a)}{b - a}(x - a) \rightarrow y = \frac{f(b) - f(a)}{b - a}(x - a) + f(a)$$
따라서, 저희는 $h$를 아래와 같이 정의할 수 있습니다.
$$h(x) = f(x) - \left( \frac{f(b) - f(a)}{b - a}(x - a) + f(a) \right)$$
이때, 롤의 정리를 적용하기 위해서는 함수 $h$가 3가지 가정을 만족하는 지 확인해야합니다.
1). 함수 $h$는 두 연속함수의 차이로 정의되므로 닫힌 구간 $[a, b]$에서 연속이다.
2). 함수 $h$는 두 미분가능한 함수의 차이로 정의되므로 열린 구간 $(a, b)$에서 연속이고 도함수는 아래와 같다.
$$h^{'}(x) = f^{'}(x) - \frac{f(b) - f(a)}{b - a}$$
3). $h(b) = f(b) - \left( \frac{f(b) - f(a)}{b - a}(b - a) + f(a)\right) = 0 = f(a) - \left( \frac{f(b) - f(a)}{b - a}(a - a) + f(a) \right) = h(a)$
따라서, 롤의 정리에 의해 열린 구간 $(a, b)$에서 $h^{'}(c) = 0$을 만족하는 $c$가 존재한다.
$$\begin{align*} 0 = h^{'}(c) = f^{'}(c) - \frac{f(b) - f(a)}{b - a} \rightarrow f^{'}(c) = \frac{f(b) - f(a)}{b - a}\end{align*}$$
따라서, 평균값의 정리가 증명됩니다.
평균값 정리는 저희에게 2가지 정리를 추가적으로 증명할 수 있게 도와줍니다.
따름정리2-1
함수 $f$의 도함수가 열린 구간 $(a ,b)$에서 $f^{'}(x) = 0$를 만족한다면 함수 $f$는 열린 구간 $(a, b)$에서 상수함수이다.
증명
$x_{1}, x_{2}$를 열린 구간 $(a, b)$에서 $x_{1} < x_{2}$를 만족하는 임의의 점이라고 두겠습니다. 이때, 함수 $f$가 열린 구간 $(a, b)$에서 미분가능하기 때문에 부열린 구간 $(x_{1}, x_{2}) \subset (a, b)$에서도 미분가능하고 부닫힌 구간 $[x_{1}, x_{2}] \subset [a, b]$에서 연속함수입니다. 이때, MVT에 의해 함수 $f$는 열린 구간 $(x_{1}, x_{2})$에서 $f^{'}(c) = \frac{f(x_{2}) - f(x_{1})}{x_{2} - x_{1}}$를 만족하는 점 $c$가 존재하기 때문에 아래와 같이 쓸 수 있죠.
$$f(x_{2}) - f(x_{1}) = f^{'}(c)(x_{2} - x_{1}) = 0$$
따라서, $f(x_{2}) = f(x_{1})$이 됩니다. 여기서 중요한 점은 저희가 두 점 $x_{1}$와 $x_{2}$를 열린 구간 $(a, b)$에서 임의로 선택했기 때문에 함수 $f$는 열린 구간 $(a, b)$ 내의 모든 점에서 같은 값을 가진다는 것을 알 수 있으므로 함수 $f$는 상수함수가 됩니다.
따름정리2-2.
두 함수 $f$와 $g$에 대해서 열린 구간 $(a, b)$에 대해서 $f^{'}(x) = g^{'}(x)$를 만족한다면 $f - g$는 열린 구간 $(a, b)$에서 상수함수이며 $f(x) = g(x) + k$와 동치이다.
증명
먼저, 함수 $F(x) = f(x) - g(x)$라고 정의하도록 하겠습니다. 그러면 함수 $F$의 도함수는 아래와 같죠.
$$F^{'}(x) = f^{'}(x) - g^{'}(x) = 0$$
이때, 따름정리2-1에 의해서 함수 $F$는 상수함수가 됩니다. 그러므로 $f - g$ 역시 상수함수가 되죠. 이는 어떤 상수 $k$에 대해서 $f(x) - g(x) = k$라는 뜻이므로 $f(x) = g(x) + k$와 동치가 됩니다.
연습문제1. 주어진 함수들과 구간에 대해서 롤의 정리를 적용하기 위한 3가지 조건이 만족함을 보이고 롤의 정리에 의해 존재하는 모든 $c$를 찾아라.
(a). $f(x) = 5 - 12x + 3x^{2}, [1, 3]$
(b). $f(x) = x^{3} - x^{2} - 6x + 2, [0, 3]$
(c). $f(x) = \sqrt{x} - \frac{1}{3}x, [0, 9]$
(d). $f(x) = \cos (2x), [\frac{\pi}{8}, \frac{7\pi}{8}]$
(a). $f(x) = 5 - 12x + 3x^{2}, [1, 3]$
1) ~ 2). 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
3). $f(1) = -4 = f(3)$
따라서, 함수 $f$는 롤의 정리에 의해 열린 구간 $(1, 3)$에서 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = -12 + 6c = 0 \rightarrow c = 2$$
(b). $f(x) = x^{3} - x^{2} - 6x + 2, [0, 3]$
1) ~ 2). 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
3). $f(0) = 2 = f(3)$
따라서, 함수 $f$는 롤의 정리에 의해 열린 구간 $(0, 3)$에서 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = 3c^{2} - 2c - 6 = 0 \rightarrow c = 2 \pm \sqrt{19}$$
(c). $f(x) = \sqrt{x} - \frac{1}{3}x, [0, 9]$
1) ~ 2). 함수 $f$는 무리함수이기 때문에 0을 포함한 양의 실수에서 연속이고 미분가능하다.
3). $f(0) = 0 = f(9)$
따라서, 함수 $f$는 롤의 정리에 의해 열린 구간 $(0, 9)$에서 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = \frac{1}{2\sqrt{c}} - \frac{1}{3} = 0 \rightarrow c = \frac{9}{4}$$
(d). $f(x) = \cos (2x), [\frac{\pi}{8}, \frac{7\pi}{8}]$
1) ~ 2). 함수 $f$는 삼각함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
3). $f(\frac{\pi}{8}) = \frac{\sqrt{2}}{2} = f(\frac{7\pi}{8})$
따라서, 함수 $f$는 롤의 정리에 의해 열린 구간 $(\frac{\pi}{8}, \frac{7\pi}{8})$에서 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = -2\sin(2x) = 0 \rightarrow c = \frac{n\pi}{2}$$
여기서 $n$은 모든 정수이다.
연습문제2. 주어진 함수들과 구간에 대해서 평균값 정리를 적용하기 위한 2가지 조건이 만족함을 보이고 평균값의 정리에 의해 존재하는 모든 $c$를 찾아라.
(a). $f(x) = 3x^{2} + 2x + 5, [-1, 1]$
(b). $f(x) = x^{3} + x - 1, [0, 2]$
(c). $f(x) = e^{-2x}, [0, 3]$
(d). $f(x) = \frac{x}{x + 2}, [1, 4]$
(a). $f(x) = 3x^{2} + 2x + 5, [-1, 1]$
1) ~ 2). 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
따라서, 함수 $f$는 평균값 정리에 의해 열린 구간 $(-1, 1)$에서 $f^{'}(c) = \frac{f(1) - f(-1)}{1 - (-1)} = 2$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = 6c + 2= 2 \rightarrow c = 0$$
(b). $f(x) = x^{3} + x - 1, [0, 2]$
1) ~ 2). 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
따라서, 함수 $f$는 평균값 정리에 의해 열린 구간 $(0, 2)$에서 $f^{'}(c) = \frac{f(2) - f(0)}{2 - 0} = 5$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = 3c^{2} + 1 = 10 \rightarrow c = \pm \sqrt{3}$$
이때, 구간에 만족하는 $c = \sqrt{3}$이 유일하게 평균값 정리를 만족하는 점이다.
(c). $f(x) = e^{-2x}, [0, 3]$
1) ~ 2). 함수 $f$는 지수함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
따라서, 함수 $f$는 평균값 정리에 의해 열린 구간 $(0, 3)$에서 $f^{'}(c) = \frac{f(3) - f(0)}{3 - 0} = \frac{e^{-6} - 1}{3}$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = -2e^{-2c} = \frac{e^{-6} - 1}{3} \rightarrow e^{2c} = \frac{6}{1 - e^{-6}} \rightarrow c = \ln \left( \sqrt{\frac{6}{1 - e^{-6}}} \right)$$
(d). $f(x) = \frac{x}{x + 2}, [1, 4]$
1) ~ 2). 함수 $f$는 유리함수이기 때문에 $x = -2$인 점을 제외한 실수 전체에서 연속이고 미분가능하다.
따라서, 함수 $f$는 평균값 정리에 의해 열린 구간 $(1, 4)$에서 $f^{'}(c) = \frac{f(4) - f(1)}{4 - 1} = \frac{\frac{1}{3}}{3} = \frac{1}{9}$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = \frac{2}{(c + 2)^{2}} = \frac{1}{9} \rightarrow c = -2 \pm 3\sqrt{2} $$
연습문제3. $1 + 2x + x^{3} + 4x^{5} = 0$이 유일한 실근을 가짐을 보여라.
$f(x) = 1 + 2x + x^{3} + 4x^{5}$라고 하면 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속함수이고 미분가능하다. 이때, $f(-1) = -6$이고 $f(1) = 8$이므로 중간값 정리 (IVT)에 의해 열린구간 $(-1, 1)$에서 $f(c) = 0$인 $c$가 적어도 하나 이상 존재한다.
주어진 방정식이 열린 구간 $(-1, 1)$에서 2개 이상의 근을 $a, b$로 가진다고 하면 $-1 < a < b < 1$을 만족한다. 따라서, $f(a) = f(b) = 0$이므로 롤의 정리에 의해 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다. 하지만, $f^{'}(x) = 20x^{4} + 3x^{2} + 2 = 0$이라고 할 때 근의 판별식이 $b^{2} - 4ac < 0$이므로 $f^{'}(c) = 0$을 만족하는 $c$가 존재하지 않는다. 이는 모순이므로 귀류법에 의해 주어진 방정식은 열린구간 $(-1, 1)$에서 유일한 실근을 갖는다.
연습문제4. $2x - 1 - \sin(x) = 0$이 유일한 실근을 가짐을 보여라.
$f(x) = 2x - 1$ 그리고 $g(x) = \sin(x)$라고 하면 $h(x) = f(x) - g(x)$로 정의하자. 여기서 함수 $h$는 다항함수와 삼각함수의 차이로 정의되기 때문에 실수 전체에서 연속함수이고 미분가능하다. 이때, $h(0) = -1 < 0$ 이고 $h(\frac{\pi}{2}) = \pi - \frac{3}{2} > 0$이므로 중간값 정리 (IVT)에 의해 $h^{'}(c) = 0$인 $c$가 열린구간 $(0, \frac{\pi}{2})$에 적어도 하나 이상 존재한다.
주어진 방정식이 열린 구간 $(0, \frac{\pi}{2})$에서 2개 이상의 근을 $a, b$로 가진다고 하면 $0 < a < b < \frac{\pi}{2}$을 만족한다. 따라서, $h(a) = h(b) = 0$이므로 롤의 정리에 의해 $h^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다. 하지만, $h^{'}(x) = 2 - \cos(x) = 0$이라고 할 때 $-1 \le \cos(x) \le 1$이므로 $h^{'}(c) = 0$을 만족하는 $c$가 존재하지 않는다. 이는 모순으므로 귀류법에 의해 주어진 방정식은 열린구간 $(0, \frac{\pi}{2})$에서 유일한 실근을 갖는다.
연습문제5. $x^{3} - 15x + c = 0$이 닫힌구간 $[-2, 2]$에서 최대 1개의 실근을 가짐을 보여라.
$f(x) = x^{3} - 15x + c$라고 하자. 이때, 닫힌구간 $[-2, 2]$에서 $f^{'}(x) = 3x^{2} - 15 < 0$이므로 함수 $f$는 닫힌구간 $[-2, 2]$에서 감소한다. 여기서 함수 $f$가 최소 2개 이상의 근을 닫힌구간 $[-2, 2]$에서 갖는다고 가정하자. 각 근을 $x = a$ 그리고 $x = b$라고 할 때 $f(a) = f(b) = 0$을 만족한다. 함수 $f$가 다항함수이기 때문에 실수전체에서 연속이고 미분가능하므로 롤의 정리를 적용하면 열린구간 $(-2, 2)$에서 $f^{'}(\alpha) = 0$을 만족하는 $\alpha$가 적어도 하나 존재해야한다. 하지만, 닫힌구간 $[-2, 2]$에서 $f^{'}(x) < 0$이므로 $f^{'}(\alpha) = 0$을 만족하는 $\alpha$는 존재할 수 없다. 이는 모순이므로 귀류법에 의해 주어진 방정식은 닫힌구간 $[-2, 2]$에서 최대 1개의 실근을 가진다.
연습문제6. $x^{4} + 4x + c = 0$이 최대 2개의 실근을 가짐을 보여라.
$f(x) = x^{4} + 4x + c$라고 하자. 이때, 함수 $f$는 다항식이므로 실수 전체에서 연속함수이고 미분가능하다. 그리고 $f^{'}(x) = 4x^{3} + 4$는 $x = -1$을 기준으로 $f^{'}(x) < 0$과 $f^{'}(x) > 0$이므로 $(-\infty, -1)$에서 함수 $f$는 감소함수이고 $(-1, \infty)$에서 함수 $f$는 증가함수이다.
이때, 함수 $f$가 최소 3개의 근을 가진다고 가정하자. 각 근을 $x = a, x = b$ 그리고 $x = c$라고 할 때, $f(a) = f(b) = f(c) = 0$과 $a < b < c$를 만족한다. 여기서 함수 $f$가 모든 실수에 대해서 연속이고 미분간응하므로 롤의 정리에 의해 $f^{'}(\alpha_{1}) = f^{'}(\alpha_{2}) = 0$인 $\alpha_{1}$와 $\alpha_{2}$가 각각 열린구간 $(a, b)$와 $(b, c)$에 적어도 하나 이상씩 존재해야한다. 하지만, $f^{'}(x) = 0$을 만족하는 점은 $x = -1$이 유일하므로 두 점 $x = \alpha_{1}$과 $x = \alpha_{2}$ㅇ[사 $f^{'}(x) = 0$을 만족할 수 없다. 이는 모순이므로 귀류법에 의해 주어진 방정식은 실수 전체에서 최대 2개의 실근을 가진다.
연습문제7. 임의의 3차 다항식이 최대 3개의 실근을 가질 수 있음을 보이고 이를 일반화하여 임의의 $n$차 다항식이 최대 $n$개의 실근을 가질 수 있음을 보여라.
1). 3차 다항식 증명
함수 $f$가 3차 다항식이라고 하면 함수 $f$는 실수 전체에서 연속함수이고 미분가능하다. 이때, $f^{'}$는 미분규칙에 의해 2차 다항식이 되므로 근 판별식에 의해 최대 2개의 근을 가질 수 있다. $f^{'}$의 각 근을 $x = \alpha_{1}$과 $x = \alpha_{2}$라고 할 때 $f^{'}(\alpha_{1}) = f^{'}(\alpha_{2}) = 0$를 만족한다.
여기서 함수 $f$가 최대 4개의 근을 가진다고 가정하자. 각 근을 $x = a_{1}, a_{2}, a_{3}$ 그리고 $x = a_{4}$라고 할 때 $f(a_{1}) = f(a_{2}) = f(a_{3}) = f(a_{4}) = 0$과 $a_{1} < a_{2} < a_{3} < a_{4}$를 만족한다. 이때, 롤의 정리에 의해 $f^{'}(x_{1}) = f^{'}(x_{2}) = f^{'}(x_{3}) = 0$인 $x_{1}, x_{2}, x_{3}$가 각 열린구간 $(\alpha_{1}, \alpha_{2}), (\alpha_{2}, \alpha_{3}), (\alpha_{3}, \alpha_{4})$에 각각 적어도 하나씩 존재한다. 하지만, $f^{'}$는 최대 2개의 근을 가질 수 있으므로 3개의 근을 가질 수 없다. 이는 모순이므로 귀류법에 의해 임의의 3차 다항식은 최대 3개의 실근을 가질 수 있다.
2). $n$차 다항식 증명
함수 $f$가 $n$차 다항식이라고 하면 함수 $f$는 실수 전체에서 연속함수이고 미분가능하다. 이때, $f^{'}$는 미분규칙에 의해 $n - 1$차 다항식이 되므로 최대 $n - 1$개의 근을 가질 수 있다. $f^{'}$의 각 근을 $x = \alpha_{i}$라고 할 때 $f^{'}(\alpha_{i}) = 0$를 만족한다. 여기서 $i = 1, 2, \dots, n - 1$이다.
여기서 함수 $f$가 최대 $n + 1$개의 근을 가진다고 가정하자. 각 근을 $x = a_{i}$고 할 때 $i = 1, 2, \dots, n + 1$에 대해서 $f(a_{i}) = 0$과 $a_{1} < a_{2} < \cdots < a_{n + 1}$를 만족한다. 이때, 롤의 정리에 의해 $f^{'}(x_{1}) = f^{'}(x_{2}) = \cdots = f^{'}(x_{n}) = 0$인 $x_{i}$가 각 열린구간 $(\alpha_{i}, \alpha_{i + 1})$에 각각 적어도 하나씩 존재한다. 하지만, $f^{'}$는 최대 $n - 1$개의 근을 가질 수 있으므로 $n$개의 근을 가질 수 없다. 이는 모순이므로 귀류법에 의해 임의의 $n$차 다항식은 최대 $n$개의 실근을 가질 수 있다.
연습문제8. $f(1) = 10$이고 $1 \le x \le 4$에 대해서 $f^{'}(x) \ge 2$를 만족할 때 $f(4)$의 최소값을 구하여라.
함수 $f$는 닫힌구간 $[1, 4]$에서 연속함수이고 열린구간 $(1, 4)$에서 미분가능하므로 평균값 정리 (MVT)에 의해 아래의 식을 만족한다.
$$\frac{f(4) - f(1)}{4 - 1} = \frac{f(4) - 10}{3} = f^{'}(c) \ge 2$$
이 부등식을 풀면 $f(4) \ge 16$이므로 $f(4)$의 최소값은 16이다.
연습문제9. 함수 $f$와 $g$가 닫힌구간 $[a, b]$에서 연속함수이고 열린구간 $(a, b)$에서 미분가능하다고 하자. 또한 $f(a) = g(a)$이고 $a < x < b$에서 $f^{'}(x) < g^{'}(x)$를 만족한다고 할 때 $f(b) < g(b)$임을 증명하라.
함수 $h = f - g$라고 정의하자. 이때, 함수 $f$와 $g$ 모두 연속함수이고 미분가능하므로 $h$ 역시 닫힌구간 $[a, b]$에서 연속함수이고 열린구간 $(a, b)$에서 미분가능하다. 따라서, 평균값 정리에 의해 $h^{'}(c) = \frac{h(b) - h(a)}{b - a}$를 만족하는 $c$가 열린구간 $(a, b)$에 적어도 하나 존재한다.
$$\begin{cases} &\frac{h(b) - h(a)}{b - a} = \frac{[f(b) - g(b)] - [f(a) - g(a)]}{b - a} = \frac{f(b) - g(b)}{b - a} \\ &h^{'}(c) = f^{'}(c) - g^{'}(c) < 0 \end{cases}$$
따라서, $\frac{f(b) - g(b)}{b - a} < 0$이므로 $f(b) < g(b)$이다.
연습문제10. $|\sin(a) - \sin(b)| \le |a - b|$임을 증명하라.
$f(x) = \sin(x)$라고 하면 함수 $f$는 실수전체에서 연속함수이고 미분가능하다. 따라서, 임의의 닫힌구간 $[a, b]$에서 함수 $f$는 연속함수이고 열린구간 $(a, b)$에서 미분가능하다. 이제 평균값 정리에 의해 아래의 식을 만족한다.
$$\begin{align*} \frac{f(b) - f(a)}{b - a} = \frac{\sin(b) - \sin(a)}{b - a} = \cos(c) \end{align*}$$
이때, $|\cos(c)| \le 1$이므로 $|\cos(c)| = \left| \frac{\sin(b) - \sin(a)}{b - a} \right| \le 1 \rightarrow |\sin(b) - \sin(a)| \le |b - a|$를 만족한다.
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 부정형 극한과 로피탈의 정리 (0) | 2021.12.22 |
|---|---|
| 미적분학 - 미분과 그래프 (0) | 2021.12.20 |
| 미적분학 - 최대값과 최소값 (0) | 2021.12.06 |
| 미적분학 - 선형근사 (2) | 2021.11.24 |
| 미적분학 - 로그함수 미분 (0) | 2021.11.23 |
안녕하세요. 지난 포스팅의 미적분학 - 최대값과 최소값에서는 전역최대 및 전역최소의 정의, 그리고 지역최대 및 지역최소의 정의, 마지막으로 임계값에 대해서 알아보았습니다. 그리고 이와 관련된 다양한 정리들(극값이론;Extreme Value Theorem, 페르마 정리;Fermat's Theorem)도 보았습니다. 오늘은 이어서 굉장히 중요하게 쓰이는 평균값 정리(Mean Value Theorem;MVT)에 대해서 알아보겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
하지만, 평균값 정리를 유도하기 전에 저희가 먼저 알아봐야 할 정리는 롤의 정리(Rolle's Theorem)입니다. 정리의 정확한 statement는 아래의 링크를 참조바랍니다.
Rolle's theorem - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search On stationary points between two equal values of a real differentiable function In calculus, Rolle's theorem or Rolle's lemma essentially states that any real-valued differentiable fun
en.wikipedia.org
정리1. 롤의 정리 (Rolle's Theorem)
함수 $f$가 아래의 3가지 조건을 만족한다고 가정하자.
1. 함수 $f$는 닫힌 구간 $[a, b]$에서 연속이다.
2. 함수 $f$는 열린 구간 $(a, b)$에서 미분가능하다.
3. $f(a) = f(b)$
위의 3가지 조건을 만족하는 함수 $f$는 열린 구간 $(a, b)$내에서 $f^{'}(c) = 0$을 만족하는 $c \in (a, b)$가 존재한다.
설명
롤의 정리는 아래의 몇 가지 함수의 예시들을 보시면 쉽게 이해하실 수 있습니다.

- 그림(a)는 모든 구간에서 상수함수입니다. 이때, 조건1, 2, 3 역시 만족하게 되죠. 또한 모든 구간에서 미분하면 0이기 때문에 $f^{'}(c) = 0$을 만족하는 $c$를 쉽게 찾을 수 있습니다.
- 그림(b)는 모든 함수값 $f(x)$가 항상 $f(a)$보다 큰 경우입니다. 그림을 보면 조건1, 2, 3 모두 만족한다는 것을 알 수 있습니다. 이 경우에는 결국에 증가했다가 다시 감소해야 $f(a) = f(b)$의 조건을 만족하게 만들 수 있습니다. 따라서 $f^{'}(x) > 0$에서 $f^{'}(x) < 0$이 되는 지점이 있기 때문에 $f^{'}(c) = 0$을 만족하는 $c$를 찾을 수 있습니다.
- 그림(c)는 몇몇 함수값 $f(x)$가 $f(a)$보다 작은 경우입니다. 이 경우에도 그림(b)와 마찬가지로 결국에는 함수의 증감이 바뀌는 지점이 있기 때문에 $f^{'}(c) = 0$을 만족하는 $c$를 찾을 수 있습니다.
- 그림(d)는 모든 함수값 $f(x)$가 $f(a)$보다 큰 경우입니다. 이 경우에도 그림(b)와 마찬가지로 결국에는 함수의 증감이 바뀌는 지점이 있기 때문에 $f^{'}(c) = 0$을 만족하는 $c$를 찾을 수 있습니다.
롤의 정리를 이해하셨다면 드디어 평균값 정리로 넘어갈 수 있습니다. 평균값 정리는 롤의 정리에서 조건을 약화시킨 일반화된 정리라고 보시면 될 거 같습니다. 정리의 정확한 statement는 아래의 링크를 참조바랍니다. 본 정리의 증명은 생략하도록 하겠습니다.
Mean value theorem - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search On the existence of a tangent to an arc parallel to the line through its endpoints In mathematics, the mean value theorem states, roughly, that for a given planar arc between two endpo
en.wikipedia.org
정리2. 평균값 정리(Mean Value Theorem; MVT)
함수 $f$가 아래의 2가지 조건을 만족한다고 가정하자.
1. 함수 $f$는 닫힌 구간 $[a, b]$에서 연속이다.
2. 함수 $f$는 열린 구간 $(a, b)$에서 미분가능하다.
위의 2가지 조건을 만족하는 함수 $f$는 열린 구간 $(a, b)$내에서 $f^{'}(c) = \frac{f(b) - f(a)}{b - a}$을 만족하는 $c \in (a, b)$가 존재한다.
증명

저희는 롤의 정리를 활용해서 평균값 정리를 증명할 수 있습니다. 따라서, 롤의 정리를 활용하기 위해 새로운 함수 $h$를 정의하도록 하겠습니다. 함수 $h$는 위 그림에서 보이는 함수 $f$와 할선 $AB$의 차이라고 정의하도록 하겠습니다. 이를 위해서는 할선 $AB$를 방정식의 형태로 써주어야겠죠? 여기서 할선 $AB$는 단순히 직선이기 때문에 아래와 같이 쓸 수 있습니다.
$$y - f(a) = \frac{f(b) - f(a)}{b - a}(x - a) \rightarrow y = \frac{f(b) - f(a)}{b - a}(x - a) + f(a)$$
따라서, 저희는 $h$를 아래와 같이 정의할 수 있습니다.
$$h(x) = f(x) - \left( \frac{f(b) - f(a)}{b - a}(x - a) + f(a) \right)$$
이때, 롤의 정리를 적용하기 위해서는 함수 $h$가 3가지 가정을 만족하는 지 확인해야합니다.
1). 함수 $h$는 두 연속함수의 차이로 정의되므로 닫힌 구간 $[a, b]$에서 연속이다.
2). 함수 $h$는 두 미분가능한 함수의 차이로 정의되므로 열린 구간 $(a, b)$에서 연속이고 도함수는 아래와 같다.
$$h^{'}(x) = f^{'}(x) - \frac{f(b) - f(a)}{b - a}$$
3). $h(b) = f(b) - \left( \frac{f(b) - f(a)}{b - a}(b - a) + f(a)\right) = 0 = f(a) - \left( \frac{f(b) - f(a)}{b - a}(a - a) + f(a) \right) = h(a)$
따라서, 롤의 정리에 의해 열린 구간 $(a, b)$에서 $h^{'}(c) = 0$을 만족하는 $c$가 존재한다.
$$\begin{align*} 0 = h^{'}(c) = f^{'}(c) - \frac{f(b) - f(a)}{b - a} \rightarrow f^{'}(c) = \frac{f(b) - f(a)}{b - a}\end{align*}$$
따라서, 평균값의 정리가 증명됩니다.
평균값 정리는 저희에게 2가지 정리를 추가적으로 증명할 수 있게 도와줍니다.
따름정리2-1
함수 $f$의 도함수가 열린 구간 $(a ,b)$에서 $f^{'}(x) = 0$를 만족한다면 함수 $f$는 열린 구간 $(a, b)$에서 상수함수이다.
증명
$x_{1}, x_{2}$를 열린 구간 $(a, b)$에서 $x_{1} < x_{2}$를 만족하는 임의의 점이라고 두겠습니다. 이때, 함수 $f$가 열린 구간 $(a, b)$에서 미분가능하기 때문에 부열린 구간 $(x_{1}, x_{2}) \subset (a, b)$에서도 미분가능하고 부닫힌 구간 $[x_{1}, x_{2}] \subset [a, b]$에서 연속함수입니다. 이때, MVT에 의해 함수 $f$는 열린 구간 $(x_{1}, x_{2})$에서 $f^{'}(c) = \frac{f(x_{2}) - f(x_{1})}{x_{2} - x_{1}}$를 만족하는 점 $c$가 존재하기 때문에 아래와 같이 쓸 수 있죠.
$$f(x_{2}) - f(x_{1}) = f^{'}(c)(x_{2} - x_{1}) = 0$$
따라서, $f(x_{2}) = f(x_{1})$이 됩니다. 여기서 중요한 점은 저희가 두 점 $x_{1}$와 $x_{2}$를 열린 구간 $(a, b)$에서 임의로 선택했기 때문에 함수 $f$는 열린 구간 $(a, b)$ 내의 모든 점에서 같은 값을 가진다는 것을 알 수 있으므로 함수 $f$는 상수함수가 됩니다.
따름정리2-2.
두 함수 $f$와 $g$에 대해서 열린 구간 $(a, b)$에 대해서 $f^{'}(x) = g^{'}(x)$를 만족한다면 $f - g$는 열린 구간 $(a, b)$에서 상수함수이며 $f(x) = g(x) + k$와 동치이다.
증명
먼저, 함수 $F(x) = f(x) - g(x)$라고 정의하도록 하겠습니다. 그러면 함수 $F$의 도함수는 아래와 같죠.
$$F^{'}(x) = f^{'}(x) - g^{'}(x) = 0$$
이때, 따름정리2-1에 의해서 함수 $F$는 상수함수가 됩니다. 그러므로 $f - g$ 역시 상수함수가 되죠. 이는 어떤 상수 $k$에 대해서 $f(x) - g(x) = k$라는 뜻이므로 $f(x) = g(x) + k$와 동치가 됩니다.
연습문제1. 주어진 함수들과 구간에 대해서 롤의 정리를 적용하기 위한 3가지 조건이 만족함을 보이고 롤의 정리에 의해 존재하는 모든 $c$를 찾아라.
(a). $f(x) = 5 - 12x + 3x^{2}, [1, 3]$
(b). $f(x) = x^{3} - x^{2} - 6x + 2, [0, 3]$
(c). $f(x) = \sqrt{x} - \frac{1}{3}x, [0, 9]$
(d). $f(x) = \cos (2x), [\frac{\pi}{8}, \frac{7\pi}{8}]$
(a). $f(x) = 5 - 12x + 3x^{2}, [1, 3]$
1) ~ 2). 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
3). $f(1) = -4 = f(3)$
따라서, 함수 $f$는 롤의 정리에 의해 열린 구간 $(1, 3)$에서 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = -12 + 6c = 0 \rightarrow c = 2$$
(b). $f(x) = x^{3} - x^{2} - 6x + 2, [0, 3]$
1) ~ 2). 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
3). $f(0) = 2 = f(3)$
따라서, 함수 $f$는 롤의 정리에 의해 열린 구간 $(0, 3)$에서 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = 3c^{2} - 2c - 6 = 0 \rightarrow c = 2 \pm \sqrt{19}$$
(c). $f(x) = \sqrt{x} - \frac{1}{3}x, [0, 9]$
1) ~ 2). 함수 $f$는 무리함수이기 때문에 0을 포함한 양의 실수에서 연속이고 미분가능하다.
3). $f(0) = 0 = f(9)$
따라서, 함수 $f$는 롤의 정리에 의해 열린 구간 $(0, 9)$에서 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = \frac{1}{2\sqrt{c}} - \frac{1}{3} = 0 \rightarrow c = \frac{9}{4}$$
(d). $f(x) = \cos (2x), [\frac{\pi}{8}, \frac{7\pi}{8}]$
1) ~ 2). 함수 $f$는 삼각함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
3). $f(\frac{\pi}{8}) = \frac{\sqrt{2}}{2} = f(\frac{7\pi}{8})$
따라서, 함수 $f$는 롤의 정리에 의해 열린 구간 $(\frac{\pi}{8}, \frac{7\pi}{8})$에서 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = -2\sin(2x) = 0 \rightarrow c = \frac{n\pi}{2}$$
여기서 $n$은 모든 정수이다.
연습문제2. 주어진 함수들과 구간에 대해서 평균값 정리를 적용하기 위한 2가지 조건이 만족함을 보이고 평균값의 정리에 의해 존재하는 모든 $c$를 찾아라.
(a). $f(x) = 3x^{2} + 2x + 5, [-1, 1]$
(b). $f(x) = x^{3} + x - 1, [0, 2]$
(c). $f(x) = e^{-2x}, [0, 3]$
(d). $f(x) = \frac{x}{x + 2}, [1, 4]$
(a). $f(x) = 3x^{2} + 2x + 5, [-1, 1]$
1) ~ 2). 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
따라서, 함수 $f$는 평균값 정리에 의해 열린 구간 $(-1, 1)$에서 $f^{'}(c) = \frac{f(1) - f(-1)}{1 - (-1)} = 2$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = 6c + 2= 2 \rightarrow c = 0$$
(b). $f(x) = x^{3} + x - 1, [0, 2]$
1) ~ 2). 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
따라서, 함수 $f$는 평균값 정리에 의해 열린 구간 $(0, 2)$에서 $f^{'}(c) = \frac{f(2) - f(0)}{2 - 0} = 5$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = 3c^{2} + 1 = 10 \rightarrow c = \pm \sqrt{3}$$
이때, 구간에 만족하는 $c = \sqrt{3}$이 유일하게 평균값 정리를 만족하는 점이다.
(c). $f(x) = e^{-2x}, [0, 3]$
1) ~ 2). 함수 $f$는 지수함수이기 때문에 실수 전체에서 연속이고 미분가능하다.
따라서, 함수 $f$는 평균값 정리에 의해 열린 구간 $(0, 3)$에서 $f^{'}(c) = \frac{f(3) - f(0)}{3 - 0} = \frac{e^{-6} - 1}{3}$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = -2e^{-2c} = \frac{e^{-6} - 1}{3} \rightarrow e^{2c} = \frac{6}{1 - e^{-6}} \rightarrow c = \ln \left( \sqrt{\frac{6}{1 - e^{-6}}} \right)$$
(d). $f(x) = \frac{x}{x + 2}, [1, 4]$
1) ~ 2). 함수 $f$는 유리함수이기 때문에 $x = -2$인 점을 제외한 실수 전체에서 연속이고 미분가능하다.
따라서, 함수 $f$는 평균값 정리에 의해 열린 구간 $(1, 4)$에서 $f^{'}(c) = \frac{f(4) - f(1)}{4 - 1} = \frac{\frac{1}{3}}{3} = \frac{1}{9}$을 만족하는 $c$가 적어도 하나 존재한다.
$$f^{'}(c) = \frac{2}{(c + 2)^{2}} = \frac{1}{9} \rightarrow c = -2 \pm 3\sqrt{2} $$
연습문제3. $1 + 2x + x^{3} + 4x^{5} = 0$이 유일한 실근을 가짐을 보여라.
$f(x) = 1 + 2x + x^{3} + 4x^{5}$라고 하면 함수 $f$는 다항함수이기 때문에 실수 전체에서 연속함수이고 미분가능하다. 이때, $f(-1) = -6$이고 $f(1) = 8$이므로 중간값 정리 (IVT)에 의해 열린구간 $(-1, 1)$에서 $f(c) = 0$인 $c$가 적어도 하나 이상 존재한다.
주어진 방정식이 열린 구간 $(-1, 1)$에서 2개 이상의 근을 $a, b$로 가진다고 하면 $-1 < a < b < 1$을 만족한다. 따라서, $f(a) = f(b) = 0$이므로 롤의 정리에 의해 $f^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다. 하지만, $f^{'}(x) = 20x^{4} + 3x^{2} + 2 = 0$이라고 할 때 근의 판별식이 $b^{2} - 4ac < 0$이므로 $f^{'}(c) = 0$을 만족하는 $c$가 존재하지 않는다. 이는 모순이므로 귀류법에 의해 주어진 방정식은 열린구간 $(-1, 1)$에서 유일한 실근을 갖는다.
연습문제4. $2x - 1 - \sin(x) = 0$이 유일한 실근을 가짐을 보여라.
$f(x) = 2x - 1$ 그리고 $g(x) = \sin(x)$라고 하면 $h(x) = f(x) - g(x)$로 정의하자. 여기서 함수 $h$는 다항함수와 삼각함수의 차이로 정의되기 때문에 실수 전체에서 연속함수이고 미분가능하다. 이때, $h(0) = -1 < 0$ 이고 $h(\frac{\pi}{2}) = \pi - \frac{3}{2} > 0$이므로 중간값 정리 (IVT)에 의해 $h^{'}(c) = 0$인 $c$가 열린구간 $(0, \frac{\pi}{2})$에 적어도 하나 이상 존재한다.
주어진 방정식이 열린 구간 $(0, \frac{\pi}{2})$에서 2개 이상의 근을 $a, b$로 가진다고 하면 $0 < a < b < \frac{\pi}{2}$을 만족한다. 따라서, $h(a) = h(b) = 0$이므로 롤의 정리에 의해 $h^{'}(c) = 0$을 만족하는 $c$가 적어도 하나 존재한다. 하지만, $h^{'}(x) = 2 - \cos(x) = 0$이라고 할 때 $-1 \le \cos(x) \le 1$이므로 $h^{'}(c) = 0$을 만족하는 $c$가 존재하지 않는다. 이는 모순으므로 귀류법에 의해 주어진 방정식은 열린구간 $(0, \frac{\pi}{2})$에서 유일한 실근을 갖는다.
연습문제5. $x^{3} - 15x + c = 0$이 닫힌구간 $[-2, 2]$에서 최대 1개의 실근을 가짐을 보여라.
$f(x) = x^{3} - 15x + c$라고 하자. 이때, 닫힌구간 $[-2, 2]$에서 $f^{'}(x) = 3x^{2} - 15 < 0$이므로 함수 $f$는 닫힌구간 $[-2, 2]$에서 감소한다. 여기서 함수 $f$가 최소 2개 이상의 근을 닫힌구간 $[-2, 2]$에서 갖는다고 가정하자. 각 근을 $x = a$ 그리고 $x = b$라고 할 때 $f(a) = f(b) = 0$을 만족한다. 함수 $f$가 다항함수이기 때문에 실수전체에서 연속이고 미분가능하므로 롤의 정리를 적용하면 열린구간 $(-2, 2)$에서 $f^{'}(\alpha) = 0$을 만족하는 $\alpha$가 적어도 하나 존재해야한다. 하지만, 닫힌구간 $[-2, 2]$에서 $f^{'}(x) < 0$이므로 $f^{'}(\alpha) = 0$을 만족하는 $\alpha$는 존재할 수 없다. 이는 모순이므로 귀류법에 의해 주어진 방정식은 닫힌구간 $[-2, 2]$에서 최대 1개의 실근을 가진다.
연습문제6. $x^{4} + 4x + c = 0$이 최대 2개의 실근을 가짐을 보여라.
$f(x) = x^{4} + 4x + c$라고 하자. 이때, 함수 $f$는 다항식이므로 실수 전체에서 연속함수이고 미분가능하다. 그리고 $f^{'}(x) = 4x^{3} + 4$는 $x = -1$을 기준으로 $f^{'}(x) < 0$과 $f^{'}(x) > 0$이므로 $(-\infty, -1)$에서 함수 $f$는 감소함수이고 $(-1, \infty)$에서 함수 $f$는 증가함수이다.
이때, 함수 $f$가 최소 3개의 근을 가진다고 가정하자. 각 근을 $x = a, x = b$ 그리고 $x = c$라고 할 때, $f(a) = f(b) = f(c) = 0$과 $a < b < c$를 만족한다. 여기서 함수 $f$가 모든 실수에 대해서 연속이고 미분간응하므로 롤의 정리에 의해 $f^{'}(\alpha_{1}) = f^{'}(\alpha_{2}) = 0$인 $\alpha_{1}$와 $\alpha_{2}$가 각각 열린구간 $(a, b)$와 $(b, c)$에 적어도 하나 이상씩 존재해야한다. 하지만, $f^{'}(x) = 0$을 만족하는 점은 $x = -1$이 유일하므로 두 점 $x = \alpha_{1}$과 $x = \alpha_{2}$ㅇ[사 $f^{'}(x) = 0$을 만족할 수 없다. 이는 모순이므로 귀류법에 의해 주어진 방정식은 실수 전체에서 최대 2개의 실근을 가진다.
연습문제7. 임의의 3차 다항식이 최대 3개의 실근을 가질 수 있음을 보이고 이를 일반화하여 임의의 $n$차 다항식이 최대 $n$개의 실근을 가질 수 있음을 보여라.
1). 3차 다항식 증명
함수 $f$가 3차 다항식이라고 하면 함수 $f$는 실수 전체에서 연속함수이고 미분가능하다. 이때, $f^{'}$는 미분규칙에 의해 2차 다항식이 되므로 근 판별식에 의해 최대 2개의 근을 가질 수 있다. $f^{'}$의 각 근을 $x = \alpha_{1}$과 $x = \alpha_{2}$라고 할 때 $f^{'}(\alpha_{1}) = f^{'}(\alpha_{2}) = 0$를 만족한다.
여기서 함수 $f$가 최대 4개의 근을 가진다고 가정하자. 각 근을 $x = a_{1}, a_{2}, a_{3}$ 그리고 $x = a_{4}$라고 할 때 $f(a_{1}) = f(a_{2}) = f(a_{3}) = f(a_{4}) = 0$과 $a_{1} < a_{2} < a_{3} < a_{4}$를 만족한다. 이때, 롤의 정리에 의해 $f^{'}(x_{1}) = f^{'}(x_{2}) = f^{'}(x_{3}) = 0$인 $x_{1}, x_{2}, x_{3}$가 각 열린구간 $(\alpha_{1}, \alpha_{2}), (\alpha_{2}, \alpha_{3}), (\alpha_{3}, \alpha_{4})$에 각각 적어도 하나씩 존재한다. 하지만, $f^{'}$는 최대 2개의 근을 가질 수 있으므로 3개의 근을 가질 수 없다. 이는 모순이므로 귀류법에 의해 임의의 3차 다항식은 최대 3개의 실근을 가질 수 있다.
2). $n$차 다항식 증명
함수 $f$가 $n$차 다항식이라고 하면 함수 $f$는 실수 전체에서 연속함수이고 미분가능하다. 이때, $f^{'}$는 미분규칙에 의해 $n - 1$차 다항식이 되므로 최대 $n - 1$개의 근을 가질 수 있다. $f^{'}$의 각 근을 $x = \alpha_{i}$라고 할 때 $f^{'}(\alpha_{i}) = 0$를 만족한다. 여기서 $i = 1, 2, \dots, n - 1$이다.
여기서 함수 $f$가 최대 $n + 1$개의 근을 가진다고 가정하자. 각 근을 $x = a_{i}$고 할 때 $i = 1, 2, \dots, n + 1$에 대해서 $f(a_{i}) = 0$과 $a_{1} < a_{2} < \cdots < a_{n + 1}$를 만족한다. 이때, 롤의 정리에 의해 $f^{'}(x_{1}) = f^{'}(x_{2}) = \cdots = f^{'}(x_{n}) = 0$인 $x_{i}$가 각 열린구간 $(\alpha_{i}, \alpha_{i + 1})$에 각각 적어도 하나씩 존재한다. 하지만, $f^{'}$는 최대 $n - 1$개의 근을 가질 수 있으므로 $n$개의 근을 가질 수 없다. 이는 모순이므로 귀류법에 의해 임의의 $n$차 다항식은 최대 $n$개의 실근을 가질 수 있다.
연습문제8. $f(1) = 10$이고 $1 \le x \le 4$에 대해서 $f^{'}(x) \ge 2$를 만족할 때 $f(4)$의 최소값을 구하여라.
함수 $f$는 닫힌구간 $[1, 4]$에서 연속함수이고 열린구간 $(1, 4)$에서 미분가능하므로 평균값 정리 (MVT)에 의해 아래의 식을 만족한다.
$$\frac{f(4) - f(1)}{4 - 1} = \frac{f(4) - 10}{3} = f^{'}(c) \ge 2$$
이 부등식을 풀면 $f(4) \ge 16$이므로 $f(4)$의 최소값은 16이다.
연습문제9. 함수 $f$와 $g$가 닫힌구간 $[a, b]$에서 연속함수이고 열린구간 $(a, b)$에서 미분가능하다고 하자. 또한 $f(a) = g(a)$이고 $a < x < b$에서 $f^{'}(x) < g^{'}(x)$를 만족한다고 할 때 $f(b) < g(b)$임을 증명하라.
함수 $h = f - g$라고 정의하자. 이때, 함수 $f$와 $g$ 모두 연속함수이고 미분가능하므로 $h$ 역시 닫힌구간 $[a, b]$에서 연속함수이고 열린구간 $(a, b)$에서 미분가능하다. 따라서, 평균값 정리에 의해 $h^{'}(c) = \frac{h(b) - h(a)}{b - a}$를 만족하는 $c$가 열린구간 $(a, b)$에 적어도 하나 존재한다.
$$\begin{cases} &\frac{h(b) - h(a)}{b - a} = \frac{[f(b) - g(b)] - [f(a) - g(a)]}{b - a} = \frac{f(b) - g(b)}{b - a} \\ &h^{'}(c) = f^{'}(c) - g^{'}(c) < 0 \end{cases}$$
따라서, $\frac{f(b) - g(b)}{b - a} < 0$이므로 $f(b) < g(b)$이다.
연습문제10. $|\sin(a) - \sin(b)| \le |a - b|$임을 증명하라.
$f(x) = \sin(x)$라고 하면 함수 $f$는 실수전체에서 연속함수이고 미분가능하다. 따라서, 임의의 닫힌구간 $[a, b]$에서 함수 $f$는 연속함수이고 열린구간 $(a, b)$에서 미분가능하다. 이제 평균값 정리에 의해 아래의 식을 만족한다.
$$\begin{align*} \frac{f(b) - f(a)}{b - a} = \frac{\sin(b) - \sin(a)}{b - a} = \cos(c) \end{align*}$$
이때, $|\cos(c)| \le 1$이므로 $|\cos(c)| = \left| \frac{\sin(b) - \sin(a)}{b - a} \right| \le 1 \rightarrow |\sin(b) - \sin(a)| \le |b - a|$를 만족한다.
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 부정형 극한과 로피탈의 정리 (0) | 2021.12.22 |
|---|---|
| 미적분학 - 미분과 그래프 (0) | 2021.12.20 |
| 미적분학 - 최대값과 최소값 (0) | 2021.12.06 |
| 미적분학 - 선형근사 (2) | 2021.11.24 |
| 미적분학 - 로그함수 미분 (0) | 2021.11.23 |
