안녕하세요. 지난 포스팅의 미적분학 - 연쇄법칙에서는 합성함수의 미분 규칙에 대해서 설명드렸습니다. 오늘은 특별한 형태의 함수인 음함수 (implicit function)이 무엇인지와 미분하는 방법에 대해서 설명드리도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
일단 음함수가 있다면 양함수(explicit function)도 있겠죠? 양함수는 일반적으로 저희가 보았던 $y = f(x)$ 꼴의 모든 함수를 의미합니다. 따라서, 음함수라는 것은 $y = f(x)$의 꼴이 아닌 함수를 의미합니다. 예를 들어 단위 원의 방정식 $x^{2} + y^{2} = 1$은 $y = f(x)$ 꼴이 아니라, $x, y$가 모든 좌항에 몰려있습니다. 이러한 함수의 꼴들을 모두 음함수라고 부릅니다.
그렇다면 바로 $x^{2} + y^{2} = 1$의 도함수 $\frac{dy}{dx}$ 를 구해보도록 하겠습니다.
$$\frac{d}{dx}(x^{2}) + \frac{d}{dx}(y^{2}) = \frac{d}{dx}(1) = 0$$
일단 $\frac{d}{dx}(x^{2}) = 2x$로 쉽게 구할 수 있습니다. 하지만 $\frac{d}{dx}(y^{2})$은 어떻게 구할까요? 아마 성급하게 0이라고 하실분들도 있겠지만 아쉽게도 틀렸습니다. 왜냐하면 $y$ 변수 자체가 $x$에 영향을 받고 있기 때문이죠. 여기서 적용해야하는 것인 지난 포스팅에서의 연쇄법칙입니다.
$$\frac{d}{dx}(y^{2}) = \frac{d}{dy}(y^{2})\frac{dy}{dx} = 2y\frac{dy}{dx}$$
따라서, 아래와 같은 식으로 쓸 수 있습니다.
$$2x + 2y \frac{dy}{dx} = 0 \Rightarrow \frac{dy}{dx} = -\frac{x}{y}$$
예제1. $x^{3} + y^{3} = 6xy$이 도함수 $\frac{dy}{dx}$를 구하여라.
$$\frac{d}{dx}(x^{3}) + \frac{d}{dx}(y^{3}) = \frac{d}{dx}(6xy)$$
위 식에서 $\frac{d}{dx}(x^{3}) = 3x^{2}$이다.
1). $\frac{d}{dx}(y^{3}) = \frac{d}{dy}(y^{3})\frac{dy}{dx} = 3y^{2}\frac{dy}{dx}$
2). $\frac{d}{dx}(6xy) = 6y\frac{d}{dx}(x) + 6x\frac{d}{dx}(y) = 6y + 6x\frac{dy}{dx}$
$$\begin{align*} &\frac{d}{dx}(x^{3}) + \frac{d}{dx}(y^{3}) = \frac{d}{dx}(6xy) \\ &\Rightarrow 3x^{2} + 3y^{2} \frac{dy}{dx} = 6y + 6x\frac{dy}{dx} \\ &\Rightarrow x^{2} + y^{2}\frac{dy}{dx} = 2y + 2x\frac{dy}{dx} \\ &\Rightarrow (y^{2} - 2x)\frac{dy}{dx} = 2y - x^{2} \\ &\Rightarrow \frac{dy}{dx} = \frac{2y - x^{2}}{y^{2} - 2x}\end{align*}$$
예제2. $x^{4} + y^{4} = 16$이 도함수 $\frac{dy}{dx}$를 구하여라.
$$\frac{d}{dx}(x^{4}) + \frac{d}{dx}(y^{4}) = \frac{d}{dx}(16)$$
위 식에서 $\frac{d}{dx}(x^{4}) = 4x^{3}$이다. 그리고 $\frac{d}{dx}(y^{4}) = \frac{d}{dy}(y^{4})\frac{dy}{dx} = 4y^{3}\frac{dy}{dx}$이다.
$$\begin{align*} &\frac{d}{dx}(x^{4}) + \frac{d}{dx}(y^{4}) = \frac{d}{dx}(16) \\ &\Rightarrow 4x^{3} + 4y^{3} \frac{dy}{dx} = 0 \\ &\Rightarrow x^{3} + y^{3}\frac{dy}{dx} = 0 \\ &\Rightarrow \frac{dy}{dx} = -\frac{x^{3}}{y^{3}} \end{align*}$$
이를 통해서 저희는 흔히 삼각함수의 역함수인 역삼각함수 (inverse trigonometric function)의 도함수도 계산할 수 있습니다. 먼저 역삼각함수의 기호는 $arc$라는 표시를 합니다. 예를 들어 사인함수의 역함수는 $\arcsin{(x)}$와 같이 쓰게 됩니다. 이와 같은 삼각함수는 $\arcsin{(x)}, \arccos{(x)}, \arctan{(x)}$와 같은 기본 삼각함수의 역함수부터 $\text{arccsc}{(x)}, \text{arcsec}{(x)}, \text{arccot}{(x)}$와 같은 고급 삼각함수의 역함수까지 다양하게 존재합니다. 또는 $\sin^{-1}{(x)}, \cos^{-1}{(x)}, \tan^{-1}{(x)}, \csc^{-1}{(x)}, \sec^{-1}{(x)}, \cot^{-1}{(x)}$와 같이도 쓸 수 있습니다. 오늘은 총 3개 함수들의 미분들을 유도하는 방법에 대해서 알아보도록 하겠습니다.
1. $y = \sin^{-1}{(x)} \Rightarrow x = \sin{(y)}$
$$\begin{align*} &\frac{d}{dx}(x) = \frac{d}{dx}(\sin{(y)}) \\ &\Rightarrow 1 = \frac{d}{dy}(\sin{(y)}) \frac{dy}{dx} \\ &\Rightarrow 1 = \cos{(y)} \frac{dy}{dx} \\ &\Rightarrow \frac{dy}{dx} = \frac{1}{\cos{(y)}} = \frac{1}{\sqrt{1 - x^{2}}}\end{align*}$$
2. $y = \cos^{-1}{(x)} \Rightarrow x = \cos{(y)}$
$$\begin{align*} &\frac{d}{dx}(x) = \frac{d}{dx}(\cos{(y)}) \\ &\Rightarrow 1 = \frac{d}{dy}(\cos{(y)}) \frac{dy}{dx} \\ &\Rightarrow 1 = -\sin{(y)} \frac{dy}{dx} \\ &\Rightarrow \frac{dy}{dx} = -\frac{1}{\sin{(y)}} = -\frac{1}{\sqrt{1 - x^{2}}}\end{align*}$$
3. $y = \tan^{-1}{(x)} \Rightarrow x = \tan{(y)}$
$$\begin{align*} &\frac{d}{dx}(x) = \frac{d}{dx}(\tan{(y)}) \\ &\Rightarrow 1 = \frac{d}{dy}(\tan{(y)}) \frac{dy}{dx} \\ &\Rightarrow 1 = \sec^{2}{(y)} \frac{dy}{dx} \\ &\Rightarrow \frac{dy}{dx} = \frac{1}{\sec^{2}{(y)}} = \frac{1}{1 + \tan^{2}{(y)}} = \frac{1}{1 + x^{2}} \end{align*}$$
4. $y = \csc^{-1}{(x)} \Rightarrow x = \csc{(y)}$
이때, $\sin^{2}{(x)} + \cos^{2}{(x)} = 1 \Rightarrow 1 + \cot^{2}{(x)} = \csc^{2}{(x)}$임을 이용합니다.
$$\begin{align*} &\frac{d}{dx}(x) = \frac{d}{dx}(\csc{(y)}) \\ &\Rightarrow 1 = \frac{d}{dy}(\csc{(y)}) \frac{dy}{dx} \\ &\Rightarrow 1 = -\cot{(y)}\csc{(y)} \frac{dy}{dx} \\ &\Rightarrow \frac{dy}{dx} = -\frac{1}{\cot{(y)}\csc{(y)}} = -\frac{1}{\csc{(y)}\sqrt{\csc^{2}{(y)} - 1}} = -\frac{1}{x\sqrt{x^{2} - 1}}\end{align*}$$
5. $y = \sec^{-1}{(x)} \Rightarrow x = \sec{(y)}$
이때, $\sin^{2}{(x)} + \cos^{2}{(x)} = 1 \Rightarrow \tan^{2}{(x)} + 1 = \sec^{2}{(x)}$임을 이용합니다.
$$\begin{align*} &\frac{d}{dx}(x) = \frac{d}{dx}(\sec{(y)}) \\ &\Rightarrow 1 = \frac{d}{dy}(\sec{(y)}) \frac{dy}{dx} \\ &\Rightarrow 1 = \tan{(y)}\sec{(y)} \frac{dy}{dx} \\ &\Rightarrow \frac{dy}{dx} = \frac{1}{\tan{(y)}\sec{(y)}} = \frac{1}{\sec{(y)}\sqrt{\sec^{2}{(y)} - 1}} = \frac{1}{x\sqrt{x^{2} - 1}}\end{align*}$$
6. $y = \cot^{-1}{(x)} \Rightarrow x = \cot{(y)}$
이때, $\sin^{2}{(x)} + \cos^{2}{(x)} = 1 \Rightarrow 1 + \cot^{2}{(x)} = \csc^{2}{(x)}$임을 이용합니다.
$$\begin{align*} &\frac{d}{dx}(x) = \frac{d}{dx}(\cot{(y)}) \\ &\Rightarrow 1 = \frac{d}{dy}(\cot{(y)}) \frac{dy}{dx} \\ &\Rightarrow 1 = -\csc^{2}{(y)} \frac{dy}{dx} \\ &\Rightarrow \frac{dy}{dx} = -\frac{1}{\csc^{2}{(y)}} = -\frac{1}{1 + \cot^{2}{(x)}} = \frac{1}{1 + x^{2}}\end{align*}$$
연습문제1. 주어진 함수들의 도함수를 구하여라.
(a). $xy + 2x + 3x^{2} = 4$
(b). $4x^{2} + 9y^{2} = 36$
(c). $\frac{1}{x} + \frac{1}{y} = 1$
(d). $\cos(x) + \sqrt{y} = 5$
(a). $xy + 2x + 3x^{2} = 4$
1). 좌항 미분 : $\frac{d}{dx} [xy + 2x + 3x^{2}] = y + x\frac{dy}{dx} + 2 + 6x$
2). 우항 미분 : $\frac{d}{dx} [4] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &y + x\frac{dy}{dx} + 2 + 6x = 0 \\ \Rightarrow& x\frac{dy}{dx} = -(6x + y + 2) \\ \Rightarrow& \frac{dy}{dx} = -\frac{6x + y + 2}{x} \end{align*}$$
(b). $4x^{2} + 9y^{2} = 36$
1). 좌항 미분 : $\frac{d}{dx} [4x^{2} + 9y^{2}] = 8x + 18y\frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} [36] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &8x + 18y\frac{dy}{dx} = 0 \\ \Rightarrow& 18y\frac{dy}{dx} = -8x \\ \Rightarrow& \frac{dy}{dx} = -\frac{4x}{9y} \end{align*}$$
(c). $\frac{1}{x} + \frac{1}{y} = 1$
1). 좌항 미분 : $\frac{d}{dx} \left[ \frac{1}{x} + \frac{1}{y} \right] = -\frac{1}{x^{2}} - \frac{1}{y^{2}}\frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} [1] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &-\frac{1}{x^{2}} - \frac{1}{y^{2}} \frac{dy}{dx} = 0 \\ \Rightarrow& \frac{1}{y^{2}}\frac{dy}{dx} = -\frac{1}{x^{2}} \\ \Rightarrow& \frac{dy}{dx} = -\frac{y^{2}}{x^{2}} \end{align*}$$
(d). $\cos(x) + \sqrt{y} = 5$
1). 좌항 미분 : $\frac{d}{dx} \left[ \cos(x) + \sqrt{y} \right] = -\sin(x) + \frac{1}{2\sqrt{y}}\frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} [5] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &-\sin(x) + \frac{1}{2\sqrt{y}} \frac{dy}{dx} = 0 \\ \Rightarrow& \frac{1}{2\sqrt{y}}\frac{dy}{dx} = \sin(x) \\ \Rightarrow& \frac{dy}{dx} = 2\sqrt{y}\sin(x) \end{align*}$$
연습문제2. 주어진 함수들의 도함수를 구하여라.
(a). $x^{3} + y^{3} = 1$
(b). $x^{2} + xy - y^{2} = 4$
(c). $x^{4}(x + y) = y^{2}(3x - y)$
(d). $x^{2}y^{2} + x\sin(y) = 4$
(e). $4\cos(x)\sin(y) = 1$
(f). $e^{\frac{x}{y}} = x - y$
(g). $\sqrt{xy} = 1 + x^{2}y$
(h). $e^{y}\cos(x) = 1 + \sin(xy)$
(a). $x^{3} + y^{3} = 1$
1). 좌항 미분 : $\frac{d}{dx} \left[ x^{3} + y^{3} \right] = 3x^{2} + 3y^{2}\frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} [1] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &3x^{2} + 3y^{2} \frac{dy}{dx} = 0 \\ \Rightarrow& 3y^{2}\frac{dy}{dx} = -3x^{2} \\ \Rightarrow& \frac{dy}{dx} = -\frac{x^{2}}{y^{2}} \end{align*}$$
(b). $x^{2} + xy - y^{2} = 4$
1). 좌항 미분 : $\frac{d}{dx} \left[ x^{2} + xy - y^{2} \right] = 2x + y + x \frac{dy}{dx} - 2y\frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} [4] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &2x + y + x \frac{dy}{dx} - 2y \frac{dy}{dx} = 0 \\ \Rightarrow& (x - 2y) \frac{dy}{dx} = -(2x + y) \\ \Rightarrow& \frac{dy}{dx} = -\frac{2x + y}{x - 2y} \end{align*}$$
(c). $x^{4}(x + y) = y^{2}(3x - y)$
1). 좌항 미분 : $\frac{d}{dx} \left[ x^{4}(x + y) = y^{2}(3x - y) \right] = 4x^{3}(x + y) + x^{4}(1 + \frac{dy}{dx})$
2). 우항 미분 : $\frac{d}{dx} \left[ y^{2}(3x - y) \right] = 2y(3x - y) \frac{dy}{dx} + y^{2}(3 - \frac{dy}{dx})$
이제 위 식을 정리한다.
$$\begin{align*} &4x^{3}(x + y) + x^{4}(1 + \frac{dy}{dx}) = 2y(3x - y) \frac{dy}{dx} + y^{2}(3 - \frac{dy}{dx}) \\ \Rightarrow& 4x^{4} + 4x^{3}y + x^{4} + x^{4} \frac{dy}{dx} = 6xy - 2y^{2} + 3y^{2} - y^{2} \frac{dy}{dx} \\ \Rightarrow& (x^{4} + y^{2})\frac{dy}{dx} = -(5x^{4} + 4x^{3}y - 6xy - y^{2}) \\ \Rightarrow& \frac{dy}{dx} = -\frac{5x^{4} + 4x^{3}y - 6xy - y^{2}}{x^{4} + y^{2}} \end{align*}$$
(d). $x^{2}y^{2} + x\sin(y) = 4$
1). 좌항 미분 : $\frac{d}{dx} \left[ x^{2}y^{2} + x\sin(y) \right] = 2xy^{2} + 2x^{2}y \frac{dy}{dx} + \sin(y) + x\cos(y) \frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} \left[ 4 \right] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &2xy^{2} + 2x^{2}y \frac{dy}{dx} + \sin(y) + x\cos(y) \frac{dy}{dx} = 0 \\ \Rightarrow& (2x^{2}y + x\cos(y)) \frac{dy}{dx} = -(2xy^{2} + \sin(y)) \\ \Rightarrow& \frac{dy}{dx} = -\frac{2xy^{2} + \sin(y)}{2x^{2}y + x\cos(y)} \end{align*}$$
(e). $4\cos(x)\sin(y) = 1$
1). 좌항 미분 : $\frac{d}{dx} \left[ 4\cos(x)\sin(y) \right] = -4\sin(x)\sin(y) + 4\cos(x)\cos(y) \frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} \left[ 1 \right] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &-4\sin(x)\sin(y) + 4\cos(x)\cos(y) \frac{dy}{dx} = 0 \\ \Rightarrow& 4\cos(x)\cos(y) \frac{dy}{dx} = 4\sin(x)\sin(y) \\ \Rightarrow& \frac{dy}{dx} = \frac{\sin(x)\sin(y)}{\cos(x)\cos(y)} = \frac{\sin(x)}{\cos(x)} \cdot \frac{\sin(y)}{\cos(y)} = \tan(x)\tan(y) \end{align*}$$
(f). $e^{\frac{x}{y}} = x - y$
1). 좌항 미분 : $\frac{d}{dx} \left[ e^{\frac{x}{y}} \right] = \frac{y - x\frac{dy}{dx}}{y^{2}} e^{\frac{x}{y}}$
2). 우항 미분 : $\frac{d}{dx} \left[ x - y \right] = 1 - \frac{dy}{dx}$
이제 위 식을 정리한다.
$$\begin{align*} &\frac{y - x\frac{dy}{dx}}{y^{2}} e^{\frac{x}{y}} = 1 - \frac{dy}{dx} \\ \Rightarrow& (y - x \frac{dy}{dx})e^{\frac{x}{y}} = y^{2} = y^{2} \frac{dy}{dx} \\ \Rightarrow& y e^{\frac{x}{y}} - x e^{\frac{x}{y}} \frac{dy}{dx} = y^{2} - y^{2} \frac{dy}{dx} \\ \Rightarrow& (y^{2} - xe^{\frac{x}{y}})\frac{dy}{dx} = y^{2} - ye^{\frac{x}{y}} \\ \Rightarrow& \frac{dy}{dx} = \frac{y^{2} - ye^{\frac{x}{y}}}{y^{2} - xe^{\frac{x}{y}}} \end{align*}$$
(g). $\sqrt{xy} = 1 + x^{2}y$
1). 좌항 미분 : $\frac{d}{dx} \left[ \sqrt{xy} \right] = \frac{y + x\frac{dy}{dx}}{2\sqrt{xy}}$
2). 우항 미분 : $\frac{d}{dx} \left[ 1 + x^{2}y \right] = 2xy + x^{2}\frac{dy}{dx}$
이제 위 식을 정리한다.
$$\begin{align*} &\frac{y + x\frac{dy}{dx}}{2\sqrt{xy}} = 2xy + x^{2}\frac{dy}{dx} \\ \Rightarrow& y + x\frac{dy}{dx} = 2\sqrt{xy}(2xy + x^{2}\frac{dy}{dx}) = 4xy\sqrt{xy} + 2x^{2}\sqrt{xy}\frac{dy}{dx} \\ \Rightarrow& (x - 2x^{2}\sqrt{xy}) \frac{dy}{dx} = -(4xy\sqrt{xy} + y) \\ \Rightarrow& \frac{dy}{dx} = -\frac{y(4x\sqrt{xy} + 1)}{x(1 - 2x\sqrt{xy})} \end{align*}$$
(h). $e^{y}\cos(x) = 1 + \sin(xy)$
1). 좌항 미분 : $\frac{d}{dx} \left[ e^{y}\cos(x) \right] = e^{y}\cos(x) \frac{dy}{dx} - e^{y}\sin(x) $
2). 우항 미분 : $\frac{d}{dx} \left[ 1 + \sin(xy) \right] = (y + x\frac{dy}{dx})\cos(xy)$
이제 위 식을 정리한다.
$$\begin{align*} &e^{y}\cos(x) \frac{dy}{dx} - e^{y}\sin(x) = (y + x \frac{dy}{dx}) \cos(xy) \\ \Rightarrow& (e^{y}\cos(x) - x\cos(xy)) \frac{dy}{dx} = y\cos(xy) + e^{y}\sin(x) \\ \Rightarrow& \frac{dy}{dx} = \frac{y\cos(xy) + e^{y}\sin(x)}{e^{y}\cos(x) - x\cos(xy)}\end{align*}$$
연습문제3. 주어진 함수들의 도함수를 구하여라.
(a). $2\sqrt{x} + \sqrt{y} = 3$
(b). $2x^{3} + x^{2}y - xy^{3} = 3$
(c). $y^{5} + x^{2}y^{3} = 1 + ye^{x^{2}}$
(d). $1 + x = \sin(xy^{2})$
(e). $y\sin(x^{2}) = x\sin(y^{2})$
(f). $\sqrt{x + y} = 1 + x^{2}y^{2}$
(g). $\tan(x - y) = \frac{y}{1 + x^{2}}$
(h). $\sin(x) + \cos(y) = \sin(x)\cos(y)$
(a). $2\sqrt{x} + \sqrt{y} = 3$
1). 좌항 미분 : $\frac{d}{dx} \left[ 2\sqrt{x} + \sqrt{y} \right] = \frac{1}{\sqrt{x}} + \frac{1}{2\sqrt{y}}\frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} [3] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &\frac{1}{\sqrt{x}} + \frac{1}{2\sqrt{y}} \frac{dy}{dx} = 0 \\ \Rightarrow& \frac{1}{2\sqrt{y}} \frac{dy}{dx} = -\frac{1}{\sqrt{x}} \\ \Rightarrow& \frac{dy}{dx} = -\frac{2\sqrt{y}}{\sqrt{x}} \end{align*}$$
(b). $2x^{3} + x^{2}y - xy^{3} = 3$
1). 좌항 미분 : $\frac{d}{dx} \left[ 2x^{3} + x^{2}y - xy^{3} \right] = 6x^{2} + 2xy + x^{2} \frac{dy}{dx} - y^{3} - 3xy^{2} \frac{dy}{dx} = (x^{2} - 3xy^{2}) \frac{dy}{dx} + (6x^{2} + 2xy - y^{3})$
2). 우항 미분 : $\frac{d}{dx} [3] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &(x^{2} - 3xy^{2})\frac{dy}{dx} + (6x^{2} + 2xy - y^{3}) = 0 \\ \Rightarrow& (x^{2} - 3xy^{2}) \frac{dy}{dx} = -(6x^{2} + 2xy - y^{3}) \\ \Rightarrow& \frac{dy}{dx} = -\frac{6x^{2} + 2xy - y^{3}}{x^{2} - 3xy^{2}} \end{align*}$$
(c). $y^{5} + x^{2}y^{3} = 1 + ye^{x^{2}}$
1). 좌항 미분 : $\frac{d}{dx} \left[ y^{5} + x^{2}y^{3} \right] = 5y^{4} \frac{dy}{dx} + 2xy^{3} + 3x^{2}y^{2} \frac{dy}{dx} = (3x^{2}y^{2} + 5y^{4}) \frac{dy}{dx} + 2xy^{3}$
2). 우항 미분 : $\frac{d}{dx} \left[ 1 + ye^{x^{2}} \right] = e^{x^{2}} \frac{dy}{dx} + 2xye^{x^{2}}$
이제 위 식을 정리한다.
$$\begin{align*} &(3x^{2}y^{2} + 5y^{4}) \frac{dy}{dx} + 2xy^{3} = e^{x^{2}} \frac{dy}{dx} + 2xye^{x^{2}} \\ \Rightarrow& (3x^{2}y^{2} + 5y^{4} - e^{x^{2}}) \frac{dy}{dx} = (2xye^{x^{2}} - 2xy^{3}) \\ \Rightarrow& \frac{dy}{dx} = -\frac{2xye^{x^{2}}}{3x^{2}y^{2} + 5y^{4} - e^{x^{2}}} \end{align*}$$
(d). $1 + x = \sin(xy^{2})$
1). 좌항 미분 : $\frac{d}{dx} \left[ 1 + x \right] = 1$
2). 우항 미분 : $\frac{d}{dx} \left[ \sin(xy) \right] = (y + x\frac{dy}{dx}) \cos(xy)$
이제 위 식을 정리한다.
$$\begin{align*} &1 = (y + x\frac{dy}{dx}) \cos(xy) = y\cos(xy) + x\cos(xy) \frac{dy}{dx} \\ \Rightarrow& x\cos(xy) \frac{dy}{dx} = 1 - y\cos(xy) \\ \Rightarrow& \frac{dy}{dx} = -\frac{1 - y\cos(xy)}{x\cos(xy)} \end{align*}$$
(e). $y\sin(x^{2}) = x\sin(y^{2})$
1). 좌항 미분 : $\frac{d}{dx} \left[ y\sin(x^{2}) \right] = \sin(x^{2}) \frac{dy}{dx} + 2xy \cos(x^{2})$
2). 우항 미분 : $\frac{d}{dx} \left[ x\sin(y^{2}) \right] = \sin(y^{2}) + 2xy \cos(y^{2}) \frac{dy}{dx}$
이제 위 식을 정리한다.
$$\begin{align*} &\sin(x^{2}) \frac{dy}{dx} + 2xy \cos(x^{2}) = \sin(y^{2}) +2xy \cos(y^{2}) \frac{dy}{dx} \\ \Rightarrow& (\sin(x^{2}) - 2xy \cos(y^{2})) \frac{dy}{dx} = \sin(y^{2}) - 2xy\cos(x^{2}) \\ \Rightarrow& \frac{dy}{dx} = -\frac{\sin(y^{2}) - 2xy\cos(x^{2})}{\sin(x^{2}) - 2xy\cos(y^{2})} \end{align*}$$
(f). $\sqrt{x + y} = 1 + x^{2}y^{2}$
1). 좌항 미분 : $\frac{d}{dx} \left[ \sqrt{x + y} \right] = \frac{1}{2\sqrt{x + y}}(1 + \frac{dy}{dx}) = \frac{1}{2\sqrt{x + y}} + \frac{1}{2\sqrt{x + y}} \frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} \left[ 1 + x^{2}y^{2} \right] = 2xy^{2} + 2x^{2}y \frac{dy}{dx}$
이제 위 식을 정리한다.
$$\begin{align*} &\frac{1}{2\sqrt{x + y}} + \frac{1}{2\sqrt{x + y}} \frac{dy}{dx} = 2xy^{2} + 2x^{2}y \frac{dy}{dx} \\ \Rightarrow& (\frac{1}{2\sqrt{x + y}} - 2x^{2}y) \frac{dy}{dx} = 2xy^{2} - \frac{1}{2\sqrt{x + y}} \\ \Rightarrow& \frac{dy}{dx} = \frac{2xy^{2} - \frac{1}{2\sqrt{x + y}}}{\frac{1}{2\sqrt{x + y}} - 2x^{2}y} = \frac{4xy^{2}\sqrt{x + y} - 1}{1 - 4xy^{2}\sqrt{x + y}}\end{align*}$$
(g). $\tan(x - y) = \frac{y}{1 + x^{2}}$
1). 좌항 미분 : $\frac{d}{dx} \left[ \tan(x - y) \right] = \sec^{2}(x - y) (1 - \frac{dy}{dx}) = \sec^{2}(x - y) - \sec^{2}(x - y) \frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} \left[ \frac{y}{1 + x^{2}} \right] = \frac{(1 + x^{2}) \frac{dy}{dx} - 2xy}{(1 + x^{2})^{2}}$
이제 위 식을 정리한다.
$$\begin{align*} &\sec^{2}(x - y) - \sec^{2}(x - y) \frac{dy}{dx} = \frac{(1 + x^{2}) \frac{dy}{dx} - 2xy}{(1 + x^{2})^{2}} \\ \Rightarrow& (1 + x^{2})^{2}\sec^{2}(x - y) - (1 + x^{2})^{2}\sec^{x}(x - y) \frac{dy}{dx} = (1 + x^{2}) \frac{dy}{dx} - 2xy \\ \Rightarrow& (1 + x^{2} + (1 + x^{2})^{2} \sec^{2}(x - y)) \frac{dy}{dx} = (1 + x^{2})^{2} \sec^{2}(x - y) + 2xy \\ \Rightarrow& \frac{dy}{dx} = \frac{(1 + x^{2})^{2} \sec^{2}(x - y) + 2xy}{1 + x^{2} + (1 + x^{2})^{2} \sec^{2}(x - y)}\end{align*}$$
(h). $\sin(x) + \cos(y) = \sin(x)\cos(y)$
1). 좌항 미분 : $\frac{d}{dx} \left[ \sin(x) + \cos(y) \right] = \cos(x) - \sin(y) \frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} \left[ \sin(x)\cos(y) \right] = \cos(x)\cos(y) - \sin(x)\sin(y) \frac{dy}{dx}$
이제 위 식을 정리한다.
$$\begin{align*} &\cos(x) - \sin(y) \frac{dy}{dx} = \cos(x)\cos(y) - \sin(x)\sin(y) \frac{dy}{dx} \\ \Rightarrow& (\sin(x)\sin(y) + \sin(y)) \frac{dy}{dx} = \cos(x)\cos(y) - \cos(x) \\ \Rightarrow& \frac{dy}{dx} = \frac{\cos(x)\cos(y) - \cos(x)}{\sin(x)\sin(y) + \sin(y)} = \frac{\cos(x)(\cos(y) - 1)}{\sin(y)(\sin(y) + 1)}\end{align*}$$
연습문제4. 주어진 소문제의 답을 구하여라.
(a). 함수 $f$가 식 $f(x) + x^{2}[f(x)]^{3} = 10$을 만족하고 $f(1) = 2$일 때 $f^{'}(1)$을 구하여라.
(b). 함수 $g$가 식 $g(x) + x\sin(g(x)) = x^{2}$을 만족할 때 $g^{'}(0)$을 구하여라.
(a). 함수 $f$가 식 $f(x) + x^{2}[f(x)]^{3} = 10$을 만족하고 $f(1) = 2$일 때 $f^{'}(1)$을 구하여라.
먼저, 함수 $f$의 도함수를 구하기 위해 양변에 미분을 취한다.
$$f^{'}(x) + 2x[f(x)]^{3} + 3x^{2}f^{'}(x)[f(x)]^{2} = 0 \Rightarrow f^{'}(1) + 2[f(1)]^{3} + 3f^{'}(1)[f(1)]^{2} = f^{'}(1) + 16 + 12f^{'}(x) = 13f^{'}(x) + 16 = 0$$
위 식을 정리하면 $f^{'}(1) = -\frac{16}{13}$임을 알 수 있다.
(b). 함수 $g$가 식 $g(x) + x\sin(g(x)) = x^{2}$을 만족할 때 $g^{'}(0)$을 구하여라.
먼저, 함수 $g$의 도함수를 구하기 위해 양변에 미분을 취한다.
1). 좌항 미분 : $\frac{d}{dx} \left[ g(x) + x\sin(g(x)) \right] = g^{'}(x) + \sin(g(x)) + xg^{'}(x)\cos(g(x))$
2). 우항 미분 : $\frac{d}{dx} \left[ x^{2} \right] = 2x$
$$g^{'}(x) + \sin(g(x)) + xg^{'}(x) \cos(g(x)) = 2x \Rightarrow g^{'}(0) = 0$$
연습문제5. 주어진 함수와 점에 대해서 접선의 방정식을 구하여라.
(a). $x^{2} + xy + y^{2} = 3, (1, 1)$
(b). $x^{2} + 2xy - y^{2} + x = 2, (1,2)$
(c). $x^{2} + y^{2} = (2x^{2} + 2y^{2} - x)^{2}, (0, \frac{1}{2})$
(a). $x^{2} + xy + y^{2} = 3, (1, 1)$
1). 좌항 미분 : $\frac{d}{dx} \left[ x^{2} + xy + y^{2} \right] = 2x + y + x \frac{dy}{dx} +2y\frac{dy}{dx} = (x + 2y) \frac{dy}{dx} + (2x + y)$
2). 우항 미분 : $\frac{d}{dx} \left[ 3 \right] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &(x + 2y)\frac{dy}{dx} + (2x + y) = 0 \\ \Rightarrow& \frac{dy}{dx} = -\frac{2x + y}{x + 2y} \end{align*}$$
이제 주어진 점에서의 접선의 기울기를 구한다.
$$m = \frac{dy}{dx}_{(1, 1)} = -1$$
따라서, 접선의 방정식은 $y = -(x - 1) + 1 = -x +2$이다.
(b). $x^{2} + 2xy - y^{2} + x = 2, (1,2)$
1). 좌항 미분 : $\frac{d}{dx} \left[ x^{2} + 2xy - y^{2} + x \right] = 2x + 2y + 2x \frac{dy}{dx} - 2y \frac{dy}{dx} + 1 = (2x - 2y) \frac{dy}{dx} (2x + 2y + 1)$
2). 우항 미분 : $\frac{d}{dx} \left[ 2 \right] = 0$
이제 위 식을 정리한다.
$$\begin{align*} &(2x - 2y)\frac{dy}{dx} + (2x + 2y + 1) = 0 \\ \Rightarrow& \frac{dy}{dx} = -\frac{2x + 2y + 1}{2x - 2y} \end{align*}$$
이제 주어진 점에서의 접선의 기울기를 구한다.
$$m = \frac{dy}{dx}_{(1, 2)} = \frac{7}{2}$$
따라서, 접선의 방정식은 $y = \frac{7}{2}(x - 1) + 2 = \frac{7}{2}x - \frac{3}{2}$이다.
(c). $x^{2} + y^{2} = (2x^{2} + 2y^{2} - x)^{2}, (0, \frac{1}{2})$
1). 좌항 미분 : $\frac{d}{dx} \left[ x^{2} + y^{2} \right] = 2x + 2y \frac{dy}{dx}$
2). 우항 미분 : $\frac{d}{dx} \left[ (2x^{2} + 2y^{2} - x)^{2} \right] = 2(4x + 4y\frac{dy}{dx} - 1)(2x^{2} + 2y^{2} - x)$
이제 위 식을 정리한다.
$$\begin{align*} &2x + 2y \frac{dy}{dx} = 2(4x + 4y \frac{dy}{dx} - 1)(2x^{2} + 2y^{2} - x) \end{align*}$$
$m = \frac{dy}{dx}_{(0, \frac{1}{2})}$을 접선의 기울기라고 할 때 주어진 점에서의 접선의 기울기를 구한다.
$$m = 2 \cdot \frac{1}{2} \cdot (2m - 1) \Rightarrow m = 1$$
따라서, 접선의 방정식은 $y = (x - 0) + \frac{1}{2} = x + \frac{1}{2}$이다.
연습문제6. 원점을 중심으로 하는 단위원 상의 임의의 점 $P$에서의 접선과 직선 $OP$는 서로 수직임을 보여라.
$P(x_{0}, y_{0})$ 그리고 단위원을 $x^{2} + y^{2} = a^{2}$라고 하자. 이때, $a$는 단위원의 반지름이다.
$$\frac{d}{dx} \left[ x^{2} + y^{2} \right] = 2x + 2y \frac{dy}{dx} = 0 \Rightarrow \frac{dy}{dx} = -\frac{x}{y}$$
따라서, 임의의 점 $P$에서의 접선의 기울기는 $m_{1} = -\frac{x_{0}}{y_{0}}$이다. 이때, 직선 $OP$의 기울기는 $m_{2} = \frac{y_{0}}{x_{0}}$이므로 두 기울기의 곱 $m_{1} \cdot m_{2} = -\frac{x_{0}}{y_{0}} \cdot \frac{y_{0}}{x_{0}} = -1$이다. 따라서, 임의의 점 $P$에서의 접선과 직선 $OP$는 서로 수직이다.
연습문제7. 주어진 함수들의 도함수를 구하여라.
(a). $y = \arctan(\sqrt{x})$
(b). $y = \arcsin(2x + 1)$
(c). $G(x) = \sqrt{1 - x^{2}}\arccos(x)$
(d). $h(t) = \text{arccot}(t) + \text{arccot} \left( \frac{1}{t} \right)$
(e). $y = \arccos(e^{2x})$
(a). $y = \arctan(\sqrt{x})$
$$\frac{dy}{dx} = \frac{d}{dx} [\arctan(\sqrt{x})] = \frac{1}{2\sqrt{x}} \cdot \frac{1}{1 +(\sqrt{x})^{2}} = \frac{1}{2\sqrt{x}(1 + x)}$$
(b). $y = \arcsin(2x + 1)$
$$\frac{dy}{dx} = \frac{d}{dx} [\arcsin(2x + 1)] = 2 \cdot \frac{1}{\sqrt{1 - (2x + 1)^{2}}} = \frac{2}{\sqrt{1 - (2x + 1)^{2}}}$$
(c). $G(x) = \sqrt{1 - x^{2}}\arccos(x)$
$$G^{'}(x) = \frac{-2x}{2\sqrt{1 - x^{2}}} \arccos(x) + \sqrt{1 - x^{2}} \cdot \left( -\frac{1}{1 - x^{2}} \right) = -\frac{x}{\sqrt{1 - x^{2}}} \arccos(x) - 1$$
(d). $h(t) = \text{arccot}(t) + \text{arccot} \left( \frac{1}{t} \right)$
$$h^{'}(t) = -\frac{1}{1 + t^{2}} - \frac{1}{1 + \left( \frac{1}{t} \right)^{2}} \cdot (- \frac{1}{t^{2}}) = -\frac{1}{1 + t^{2}} + \frac{1}{1 + t^{2}} = 0$$
(e). $y = \arccos(e^{2x})$
$$\frac{dy}{dx} = \frac{d}{dx} \left[ \arccos(e^{2x}) \right] = -\frac{2e^{2x}}{\sqrt{1 - e^{4x}}}$$
연습문제8. 주어진 함수들의 도함수를 구하여라.
(a). $y = \sqrt{\arctan(x)}$
(b). $g(x) = \sqrt{x^{2} - 1}\text{arcsec}(x)$
(c). $y = \arctan(x - \sqrt{1 + x^{2}})$
(d). $F(\theta) = \arcsin (\sqrt{\sin(\theta)})$
(e). $y = \arctan \left( \frac{1 - x}{1 + x} \right)$
(a). $y = \sqrt{\arctan(x)}$
$$\frac{dy}{dx} = \frac{1}{2\sqrt{\arctan(x)}} \cdot \frac{1}{1 + x^{2}} = \frac{1}{2(1 + x^{2})\sqrt{\arctan(x)}}$$
(b). $g(x) = \sqrt{x^{2} - 1}\text{arcsec}(x)$
$$g^{'}(x) = \frac{2x}{2\sqrt{x^{2} - 1}} \text{arcsec}(x) + \sqrt{x^{2} - 1} \cdot \frac{1}{x\sqrt{x^{2} - 1}} = \frac{x\text{arcsec}(x)}{\sqrt{x^{2} - 1}} +\frac{1}{x}$$
(c). $y = \arctan(x - \sqrt{1 + x^{2}})$
$$\frac{dy}{dx} = \frac{1}{1 + (x - \sqrt{1 + x^{2}})^{2}} \cdot (1 - \frac{x}{\sqrt{1 + x^{2}}})$$
(d). $F(\theta) = \arcsin (\sqrt{\sin(\theta)})$
$$F^{'}(\theta) = \cos(\theta) \cdot \frac{1}{2\sqrt{\sin(\theta)}} \cdot \frac{1}{\sqrt{1 - (\sqrt{\sin(\theta)})^{2}}} = \frac{\cos(\theta)}{2\sqrt{\sin(\theta)}} \cdot \frac{1}{\cos(\theta)} = \frac{1}{2\sqrt{\sin(\theta)}}$$
(e). $y = \arctan \left( \frac{1 - x}{1 + x} \right)$
$$\frac{dy}{dx} = \frac{1}{1 + \left( \frac{1 - x}{1 + x} \right)^{2}} \cdot \frac{-(1 + x) - (1 - x)}{(1 + x)^{2}}= -\frac{1}{2(1 +x)} \sqrt{\frac{1 + x}{1 - x}}$$
연습문제9. 함수 $f$가 일대일 대응인 미분가능한 함수이고 역함수 $f^{-1}$ 역시 미분가능한 함수라고 할 때, $(f^{-1})^{'}(x) = \frac{1}{f^{'}(f^{-1})(x)}$임을 보여라.
$y = f^{-1}(x)$라고 하면 역함수의 정의에 의해 $x = f(y)$라고 할 수 있다. 이제 양변에 대해 미분을 취하면 $1 = f^{'}(y) \frac{dy}{dx}$를 얻을 수 있고, 이 식을 다시 정리하면 $(f^{-1})^{'}(x) = y^{'} = \frac{dy}{dx} = \frac{1}{f^{'}(y)} = \frac{1}{f^{'}(f^{-1}(x))}$이다.
연습문제10. 아래의 그림에서 원을 중심으로 하는 타원의 방정식을 $x^{2} + 4y^{2} = 5$라고 하자. $(3, 0)$ 위치의 높이를 모르는 가로등이 타원을 비칠 때 그림자의 경계가 $x = -5$에서 생긴다고 할 때 가로등의 높이를 구하여라.
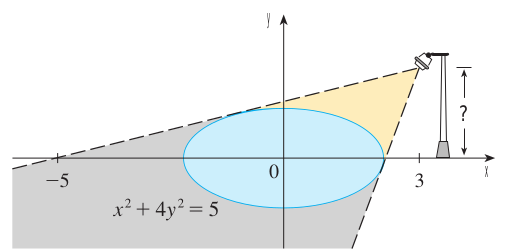
주어진 타원의 도함수를 먼저 구한다.
$$2x + 8y \frac{dy}{dx} = 0 \rightarrow \frac{dy}{dx} = -\frac{x}{4y}$$
이때, 타원과 전등에 의해 만들어지는 두 접선 중 $(-5, 0)$을 지나는 접선의 방정식을 먼저 구해야한다. 해당 접선의 기울기를 $m$이라고 할 때 아래와 같이 접선의 방정식을 구할 수 있다.
$$\begin{align*} &y = m(x + 5) = mx + 5m \\ \Rightarrow& y = \left( -\frac{x_{0}}{4y_{0}} \right)x + 5 \cdot \left( -\frac{x_{0}}{4y_{0}} \right) \\ \Rightarrow& 4y_{0}y = -x_{0}x - 5x_{0} \end{align*}$$
위 마지막 식에서 $(x_{0}, y_{0})$을 대입한다.
$$4y_{0}^{2} + x_{0}^{2} = 5 = -5x_{0}$$
따라서, $(x_{0}, y_{0}) = (-1, 1)$이다. 그러므로 해당 점에서의 접선의 방정식은 $y = \frac{1}{4}x + \frac{5}{4}$이다. 이때, 가로등은 $x = 3$ 위치에 존재하므로 이를 접선의 방정식에 대입하면 가로등의 높이를 얻을 수 있다. 따라서 가로등의 높이는 $h = \frac{3}{4} + \frac{5}{4} = 2$이다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.09.12 : 전체적인 스타일 수정
22.09.13 : 연습문제1-5 추가
22.09.14 : 연습문제6-10 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 선형근사 (2) | 2021.11.24 |
|---|---|
| 미적분학 - 로그함수 미분 (0) | 2021.11.23 |
| 미적분학 - 연쇄 법칙 (0) | 2021.11.09 |
| 미적분학 - 삼각함수 미분 (0) | 2021.11.02 |
| 미적분학 - 곱의 미분과 몫 미분 (0) | 2021.10.29 |
안녕하세요. 지난 포스팅의 미적분학 - 연쇄법칙에서는 합성함수의 미분 규칙에 대해서 설명드렸습니다. 오늘은 특별한 형태의 함수인 음함수 (implicit function)이 무엇인지와 미분하는 방법에 대해서 설명드리도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
일단 음함수가 있다면 양함수(explicit function)도 있겠죠? 양함수는 일반적으로 저희가 보았던 y=f(x) 꼴의 모든 함수를 의미합니다. 따라서, 음함수라는 것은 y=f(x)의 꼴이 아닌 함수를 의미합니다. 예를 들어 단위 원의 방정식 x2+y2=1은 y=f(x) 꼴이 아니라, x,y가 모든 좌항에 몰려있습니다. 이러한 함수의 꼴들을 모두 음함수라고 부릅니다.
그렇다면 바로 x2+y2=1의 도함수 dydx 를 구해보도록 하겠습니다.
ddx(x2)+ddx(y2)=ddx(1)=0
일단 ddx(x2)=2x로 쉽게 구할 수 있습니다. 하지만 ddx(y2)은 어떻게 구할까요? 아마 성급하게 0이라고 하실분들도 있겠지만 아쉽게도 틀렸습니다. 왜냐하면 y 변수 자체가 x에 영향을 받고 있기 때문이죠. 여기서 적용해야하는 것인 지난 포스팅에서의 연쇄법칙입니다.
ddx(y2)=ddy(y2)dydx=2ydydx
따라서, 아래와 같은 식으로 쓸 수 있습니다.
2x+2ydydx=0⇒dydx=−xy
예제1. x3+y3=6xy이 도함수 dydx를 구하여라.
ddx(x3)+ddx(y3)=ddx(6xy)
위 식에서 ddx(x3)=3x2이다.
1). ddx(y3)=ddy(y3)dydx=3y2dydx
2). ddx(6xy)=6yddx(x)+6xddx(y)=6y+6xdydx
ddx(x3)+ddx(y3)=ddx(6xy)⇒3x2+3y2dydx=6y+6xdydx⇒x2+y2dydx=2y+2xdydx⇒(y2−2x)dydx=2y−x2⇒dydx=2y−x2y2−2x
예제2. x4+y4=16이 도함수 dydx를 구하여라.
ddx(x4)+ddx(y4)=ddx(16)
위 식에서 ddx(x4)=4x3이다. 그리고 ddx(y4)=ddy(y4)dydx=4y3dydx이다.
ddx(x4)+ddx(y4)=ddx(16)⇒4x3+4y3dydx=0⇒x3+y3dydx=0⇒dydx=−x3y3
이를 통해서 저희는 흔히 삼각함수의 역함수인 역삼각함수 (inverse trigonometric function)의 도함수도 계산할 수 있습니다. 먼저 역삼각함수의 기호는 arc라는 표시를 합니다. 예를 들어 사인함수의 역함수는 arcsin(x)와 같이 쓰게 됩니다. 이와 같은 삼각함수는 arcsin(x),arccos(x),arctan(x)와 같은 기본 삼각함수의 역함수부터 arccsc(x),arcsec(x),arccot(x)와 같은 고급 삼각함수의 역함수까지 다양하게 존재합니다. 또는 sin−1(x),cos−1(x),tan−1(x),csc−1(x),sec−1(x),cot−1(x)와 같이도 쓸 수 있습니다. 오늘은 총 3개 함수들의 미분들을 유도하는 방법에 대해서 알아보도록 하겠습니다.
1. y=sin−1(x)⇒x=sin(y)
ddx(x)=ddx(sin(y))⇒1=ddy(sin(y))dydx⇒1=cos(y)dydx⇒dydx=1cos(y)=1√1−x2
2. y=cos−1(x)⇒x=cos(y)
ddx(x)=ddx(cos(y))⇒1=ddy(cos(y))dydx⇒1=−sin(y)dydx⇒dydx=−1sin(y)=−1√1−x2
3. y=tan−1(x)⇒x=tan(y)
ddx(x)=ddx(tan(y))⇒1=ddy(tan(y))dydx⇒1=sec2(y)dydx⇒dydx=1sec2(y)=11+tan2(y)=11+x2
4. y=csc−1(x)⇒x=csc(y)
이때, sin2(x)+cos2(x)=1⇒1+cot2(x)=csc2(x)임을 이용합니다.
ddx(x)=ddx(csc(y))⇒1=ddy(csc(y))dydx⇒1=−cot(y)csc(y)dydx⇒dydx=−1cot(y)csc(y)=−1csc(y)√csc2(y)−1=−1x√x2−1
5. y=sec−1(x)⇒x=sec(y)
이때, sin2(x)+cos2(x)=1⇒tan2(x)+1=sec2(x)임을 이용합니다.
ddx(x)=ddx(sec(y))⇒1=ddy(sec(y))dydx⇒1=tan(y)sec(y)dydx⇒dydx=1tan(y)sec(y)=1sec(y)√sec2(y)−1=1x√x2−1
6. y=cot−1(x)⇒x=cot(y)
이때, sin2(x)+cos2(x)=1⇒1+cot2(x)=csc2(x)임을 이용합니다.
ddx(x)=ddx(cot(y))⇒1=ddy(cot(y))dydx⇒1=−csc2(y)dydx⇒dydx=−1csc2(y)=−11+cot2(x)=11+x2
연습문제1. 주어진 함수들의 도함수를 구하여라.
(a). xy+2x+3x2=4
(b). 4x2+9y2=36
(c). 1x+1y=1
(d). cos(x)+√y=5
(a). xy+2x+3x2=4
1). 좌항 미분 : ddx[xy+2x+3x2]=y+xdydx+2+6x
2). 우항 미분 : ddx[4]=0
이제 위 식을 정리한다.
y+xdydx+2+6x=0⇒xdydx=−(6x+y+2)⇒dydx=−6x+y+2x
(b). 4x2+9y2=36
1). 좌항 미분 : ddx[4x2+9y2]=8x+18ydydx
2). 우항 미분 : ddx[36]=0
이제 위 식을 정리한다.
8x+18ydydx=0⇒18ydydx=−8x⇒dydx=−4x9y
(c). 1x+1y=1
1). 좌항 미분 : ddx[1x+1y]=−1x2−1y2dydx
2). 우항 미분 : ddx[1]=0
이제 위 식을 정리한다.
−1x2−1y2dydx=0⇒1y2dydx=−1x2⇒dydx=−y2x2
(d). cos(x)+√y=5
1). 좌항 미분 : ddx[cos(x)+√y]=−sin(x)+12√ydydx
2). 우항 미분 : ddx[5]=0
이제 위 식을 정리한다.
−sin(x)+12√ydydx=0⇒12√ydydx=sin(x)⇒dydx=2√ysin(x)
연습문제2. 주어진 함수들의 도함수를 구하여라.
(a). x3+y3=1
(b). x2+xy−y2=4
(c). x4(x+y)=y2(3x−y)
(d). x2y2+xsin(y)=4
(e). 4cos(x)sin(y)=1
(f). exy=x−y
(g). √xy=1+x2y
(h). eycos(x)=1+sin(xy)
(a). x3+y3=1
1). 좌항 미분 : ddx[x3+y3]=3x2+3y2dydx
2). 우항 미분 : ddx[1]=0
이제 위 식을 정리한다.
3x2+3y2dydx=0⇒3y2dydx=−3x2⇒dydx=−x2y2
(b). x2+xy−y2=4
1). 좌항 미분 : ddx[x2+xy−y2]=2x+y+xdydx−2ydydx
2). 우항 미분 : ddx[4]=0
이제 위 식을 정리한다.
2x+y+xdydx−2ydydx=0⇒(x−2y)dydx=−(2x+y)⇒dydx=−2x+yx−2y
(c). x4(x+y)=y2(3x−y)
1). 좌항 미분 : ddx[x4(x+y)=y2(3x−y)]=4x3(x+y)+x4(1+dydx)
2). 우항 미분 : ddx[y2(3x−y)]=2y(3x−y)dydx+y2(3−dydx)
이제 위 식을 정리한다.
4x3(x+y)+x4(1+dydx)=2y(3x−y)dydx+y2(3−dydx)⇒4x4+4x3y+x4+x4dydx=6xy−2y2+3y2−y2dydx⇒(x4+y2)dydx=−(5x4+4x3y−6xy−y2)⇒dydx=−5x4+4x3y−6xy−y2x4+y2
(d). x2y2+xsin(y)=4
1). 좌항 미분 : ddx[x2y2+xsin(y)]=2xy2+2x2ydydx+sin(y)+xcos(y)dydx
2). 우항 미분 : ddx[4]=0
이제 위 식을 정리한다.
2xy2+2x2ydydx+sin(y)+xcos(y)dydx=0⇒(2x2y+xcos(y))dydx=−(2xy2+sin(y))⇒dydx=−2xy2+sin(y)2x2y+xcos(y)
(e). 4cos(x)sin(y)=1
1). 좌항 미분 : ddx[4cos(x)sin(y)]=−4sin(x)sin(y)+4cos(x)cos(y)dydx
2). 우항 미분 : ddx[1]=0
이제 위 식을 정리한다.
−4sin(x)sin(y)+4cos(x)cos(y)dydx=0⇒4cos(x)cos(y)dydx=4sin(x)sin(y)⇒dydx=sin(x)sin(y)cos(x)cos(y)=sin(x)cos(x)⋅sin(y)cos(y)=tan(x)tan(y)
(f). exy=x−y
1). 좌항 미분 : ddx[exy]=y−xdydxy2exy
2). 우항 미분 : ddx[x−y]=1−dydx
이제 위 식을 정리한다.
y−xdydxy2exy=1−dydx⇒(y−xdydx)exy=y2=y2dydx⇒yexy−xexydydx=y2−y2dydx⇒(y2−xexy)dydx=y2−yexy⇒dydx=y2−yexyy2−xexy
(g). √xy=1+x2y
1). 좌항 미분 : ddx[√xy]=y+xdydx2√xy
2). 우항 미분 : ddx[1+x2y]=2xy+x2dydx
이제 위 식을 정리한다.
y+xdydx2√xy=2xy+x2dydx⇒y+xdydx=2√xy(2xy+x2dydx)=4xy√xy+2x2√xydydx⇒(x−2x2√xy)dydx=−(4xy√xy+y)⇒dydx=−y(4x√xy+1)x(1−2x√xy)
(h). eycos(x)=1+sin(xy)
1). 좌항 미분 : ddx[eycos(x)]=eycos(x)dydx−eysin(x)
2). 우항 미분 : ddx[1+sin(xy)]=(y+xdydx)cos(xy)
이제 위 식을 정리한다.
eycos(x)dydx−eysin(x)=(y+xdydx)cos(xy)⇒(eycos(x)−xcos(xy))dydx=ycos(xy)+eysin(x)⇒dydx=ycos(xy)+eysin(x)eycos(x)−xcos(xy)
연습문제3. 주어진 함수들의 도함수를 구하여라.
(a). 2√x+√y=3
(b). 2x3+x2y−xy3=3
(c). y5+x2y3=1+yex2
(d). 1+x=sin(xy2)
(e). ysin(x2)=xsin(y2)
(f). √x+y=1+x2y2
(g). tan(x−y)=y1+x2
(h). sin(x)+cos(y)=sin(x)cos(y)
(a). 2√x+√y=3
1). 좌항 미분 : ddx[2√x+√y]=1√x+12√ydydx
2). 우항 미분 : ddx[3]=0
이제 위 식을 정리한다.
1√x+12√ydydx=0⇒12√ydydx=−1√x⇒dydx=−2√y√x
(b). 2x3+x2y−xy3=3
1). 좌항 미분 : ddx[2x3+x2y−xy3]=6x2+2xy+x2dydx−y3−3xy2dydx=(x2−3xy2)dydx+(6x2+2xy−y3)
2). 우항 미분 : ddx[3]=0
이제 위 식을 정리한다.
(x2−3xy2)dydx+(6x2+2xy−y3)=0⇒(x2−3xy2)dydx=−(6x2+2xy−y3)⇒dydx=−6x2+2xy−y3x2−3xy2
(c). y5+x2y3=1+yex2
1). 좌항 미분 : ddx[y5+x2y3]=5y4dydx+2xy3+3x2y2dydx=(3x2y2+5y4)dydx+2xy3
2). 우항 미분 : ddx[1+yex2]=ex2dydx+2xyex2
이제 위 식을 정리한다.
(3x2y2+5y4)dydx+2xy3=ex2dydx+2xyex2⇒(3x2y2+5y4−ex2)dydx=(2xyex2−2xy3)⇒dydx=−2xyex23x2y2+5y4−ex2
(d). 1+x=sin(xy2)
1). 좌항 미분 : ddx[1+x]=1
2). 우항 미분 : ddx[sin(xy)]=(y+xdydx)cos(xy)
이제 위 식을 정리한다.
1=(y+xdydx)cos(xy)=ycos(xy)+xcos(xy)dydx⇒xcos(xy)dydx=1−ycos(xy)⇒dydx=−1−ycos(xy)xcos(xy)
(e). ysin(x2)=xsin(y2)
1). 좌항 미분 : ddx[ysin(x2)]=sin(x2)dydx+2xycos(x2)
2). 우항 미분 : ddx[xsin(y2)]=sin(y2)+2xycos(y2)dydx
이제 위 식을 정리한다.
sin(x2)dydx+2xycos(x2)=sin(y2)+2xycos(y2)dydx⇒(sin(x2)−2xycos(y2))dydx=sin(y2)−2xycos(x2)⇒dydx=−sin(y2)−2xycos(x2)sin(x2)−2xycos(y2)
(f). √x+y=1+x2y2
1). 좌항 미분 : ddx[√x+y]=12√x+y(1+dydx)=12√x+y+12√x+ydydx
2). 우항 미분 : ddx[1+x2y2]=2xy2+2x2ydydx
이제 위 식을 정리한다.
12√x+y+12√x+ydydx=2xy2+2x2ydydx⇒(12√x+y−2x2y)dydx=2xy2−12√x+y⇒dydx=2xy2−12√x+y12√x+y−2x2y=4xy2√x+y−11−4xy2√x+y
(g). tan(x−y)=y1+x2
1). 좌항 미분 : ddx[tan(x−y)]=sec2(x−y)(1−dydx)=sec2(x−y)−sec2(x−y)dydx
2). 우항 미분 : ddx[y1+x2]=(1+x2)dydx−2xy(1+x2)2
이제 위 식을 정리한다.
sec2(x−y)−sec2(x−y)dydx=(1+x2)dydx−2xy(1+x2)2⇒(1+x2)2sec2(x−y)−(1+x2)2secx(x−y)dydx=(1+x2)dydx−2xy⇒(1+x2+(1+x2)2sec2(x−y))dydx=(1+x2)2sec2(x−y)+2xy⇒dydx=(1+x2)2sec2(x−y)+2xy1+x2+(1+x2)2sec2(x−y)
(h). sin(x)+cos(y)=sin(x)cos(y)
1). 좌항 미분 : ddx[sin(x)+cos(y)]=cos(x)−sin(y)dydx
2). 우항 미분 : ddx[sin(x)cos(y)]=cos(x)cos(y)−sin(x)sin(y)dydx
이제 위 식을 정리한다.
cos(x)−sin(y)dydx=cos(x)cos(y)−sin(x)sin(y)dydx⇒(sin(x)sin(y)+sin(y))dydx=cos(x)cos(y)−cos(x)⇒dydx=cos(x)cos(y)−cos(x)sin(x)sin(y)+sin(y)=cos(x)(cos(y)−1)sin(y)(sin(y)+1)
연습문제4. 주어진 소문제의 답을 구하여라.
(a). 함수 f가 식 f(x)+x2[f(x)]3=10을 만족하고 f(1)=2일 때 f′(1)을 구하여라.
(b). 함수 g가 식 g(x)+xsin(g(x))=x2을 만족할 때 g′(0)을 구하여라.
(a). 함수 f가 식 f(x)+x2[f(x)]3=10을 만족하고 f(1)=2일 때 f′(1)을 구하여라.
먼저, 함수 f의 도함수를 구하기 위해 양변에 미분을 취한다.
f′(x)+2x[f(x)]3+3x2f′(x)[f(x)]2=0⇒f′(1)+2[f(1)]3+3f′(1)[f(1)]2=f′(1)+16+12f′(x)=13f′(x)+16=0
위 식을 정리하면 f′(1)=−1613임을 알 수 있다.
(b). 함수 g가 식 g(x)+xsin(g(x))=x2을 만족할 때 g′(0)을 구하여라.
먼저, 함수 g의 도함수를 구하기 위해 양변에 미분을 취한다.
1). 좌항 미분 : ddx[g(x)+xsin(g(x))]=g′(x)+sin(g(x))+xg′(x)cos(g(x))
2). 우항 미분 : ddx[x2]=2x
g′(x)+sin(g(x))+xg′(x)cos(g(x))=2x⇒g′(0)=0
연습문제5. 주어진 함수와 점에 대해서 접선의 방정식을 구하여라.
(a). x2+xy+y2=3,(1,1)
(b). x2+2xy−y2+x=2,(1,2)
(c). x2+y2=(2x2+2y2−x)2,(0,12)
(a). x2+xy+y2=3,(1,1)
1). 좌항 미분 : ddx[x2+xy+y2]=2x+y+xdydx+2ydydx=(x+2y)dydx+(2x+y)
2). 우항 미분 : ddx[3]=0
이제 위 식을 정리한다.
(x+2y)dydx+(2x+y)=0⇒dydx=−2x+yx+2y
이제 주어진 점에서의 접선의 기울기를 구한다.
m=dydx(1,1)=−1
따라서, 접선의 방정식은 y=−(x−1)+1=−x+2이다.
(b). x2+2xy−y2+x=2,(1,2)
1). 좌항 미분 : ddx[x2+2xy−y2+x]=2x+2y+2xdydx−2ydydx+1=(2x−2y)dydx(2x+2y+1)
2). 우항 미분 : ddx[2]=0
이제 위 식을 정리한다.
(2x−2y)dydx+(2x+2y+1)=0⇒dydx=−2x+2y+12x−2y
이제 주어진 점에서의 접선의 기울기를 구한다.
m=dydx(1,2)=72
따라서, 접선의 방정식은 y=72(x−1)+2=72x−32이다.
(c). x2+y2=(2x2+2y2−x)2,(0,12)
1). 좌항 미분 : ddx[x2+y2]=2x+2ydydx
2). 우항 미분 : ddx[(2x2+2y2−x)2]=2(4x+4ydydx−1)(2x2+2y2−x)
이제 위 식을 정리한다.
2x+2ydydx=2(4x+4ydydx−1)(2x2+2y2−x)
$m = \frac{dy}{dx}_{(0, \frac{1}{2})}$을 접선의 기울기라고 할 때 주어진 점에서의 접선의 기울기를 구한다.
m=2⋅12⋅(2m−1)⇒m=1
따라서, 접선의 방정식은 y=(x−0)+12=x+12이다.
연습문제6. 원점을 중심으로 하는 단위원 상의 임의의 점 P에서의 접선과 직선 OP는 서로 수직임을 보여라.
P(x0,y0) 그리고 단위원을 x2+y2=a2라고 하자. 이때, a는 단위원의 반지름이다.
ddx[x2+y2]=2x+2ydydx=0⇒dydx=−xy
따라서, 임의의 점 P에서의 접선의 기울기는 m1=−x0y0이다. 이때, 직선 OP의 기울기는 m2=y0x0이므로 두 기울기의 곱 m1⋅m2=−x0y0⋅y0x0=−1이다. 따라서, 임의의 점 P에서의 접선과 직선 OP는 서로 수직이다.
연습문제7. 주어진 함수들의 도함수를 구하여라.
(a). y=arctan(√x)
(b). y=arcsin(2x+1)
(c). G(x)=√1−x2arccos(x)
(d). h(t)=arccot(t)+arccot(1t)
(e). y=arccos(e2x)
(a). y=arctan(√x)
dydx=ddx[arctan(√x)]=12√x⋅11+(√x)2=12√x(1+x)
(b). y=arcsin(2x+1)
dydx=ddx[arcsin(2x+1)]=2⋅1√1−(2x+1)2=2√1−(2x+1)2
(c). G(x)=√1−x2arccos(x)
G′(x)=−2x2√1−x2arccos(x)+√1−x2⋅(−11−x2)=−x√1−x2arccos(x)−1
(d). h(t)=arccot(t)+arccot(1t)
h′(t)=−11+t2−11+(1t)2⋅(−1t2)=−11+t2+11+t2=0
(e). y=arccos(e2x)
dydx=ddx[arccos(e2x)]=−2e2x√1−e4x
연습문제8. 주어진 함수들의 도함수를 구하여라.
(a). y=√arctan(x)
(b). g(x)=√x2−1arcsec(x)
(c). y=arctan(x−√1+x2)
(d). F(θ)=arcsin(√sin(θ))
(e). y=arctan(1−x1+x)
(a). y=√arctan(x)
dydx=12√arctan(x)⋅11+x2=12(1+x2)√arctan(x)
(b). g(x)=√x2−1arcsec(x)
g′(x)=2x2√x2−1arcsec(x)+√x2−1⋅1x√x2−1=xarcsec(x)√x2−1+1x
(c). y=arctan(x−√1+x2)
dydx=11+(x−√1+x2)2⋅(1−x√1+x2)
(d). F(θ)=arcsin(√sin(θ))
F′(θ)=cos(θ)⋅12√sin(θ)⋅1√1−(√sin(θ))2=cos(θ)2√sin(θ)⋅1cos(θ)=12√sin(θ)
(e). y=arctan(1−x1+x)
dydx=11+(1−x1+x)2⋅−(1+x)−(1−x)(1+x)2=−12(1+x)√1+x1−x
연습문제9. 함수 f가 일대일 대응인 미분가능한 함수이고 역함수 f−1 역시 미분가능한 함수라고 할 때, (f−1)′(x)=1f′(f−1)(x)임을 보여라.
y=f−1(x)라고 하면 역함수의 정의에 의해 x=f(y)라고 할 수 있다. 이제 양변에 대해 미분을 취하면 1=f′(y)dydx를 얻을 수 있고, 이 식을 다시 정리하면 (f−1)′(x)=y′=dydx=1f′(y)=1f′(f−1(x))이다.
연습문제10. 아래의 그림에서 원을 중심으로 하는 타원의 방정식을 x2+4y2=5라고 하자. (3,0) 위치의 높이를 모르는 가로등이 타원을 비칠 때 그림자의 경계가 x=−5에서 생긴다고 할 때 가로등의 높이를 구하여라.
주어진 타원의 도함수를 먼저 구한다.
2x+8ydydx=0→dydx=−x4y
이때, 타원과 전등에 의해 만들어지는 두 접선 중 (−5,0)을 지나는 접선의 방정식을 먼저 구해야한다. 해당 접선의 기울기를 m이라고 할 때 아래와 같이 접선의 방정식을 구할 수 있다.
y=m(x+5)=mx+5m⇒y=(−x04y0)x+5⋅(−x04y0)⇒4y0y=−x0x−5x0
위 마지막 식에서 (x0,y0)을 대입한다.
4y20+x20=5=−5x0
따라서, (x0,y0)=(−1,1)이다. 그러므로 해당 점에서의 접선의 방정식은 y=14x+54이다. 이때, 가로등은 x=3 위치에 존재하므로 이를 접선의 방정식에 대입하면 가로등의 높이를 얻을 수 있다. 따라서 가로등의 높이는 h=34+54=2이다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.09.12 : 전체적인 스타일 수정
22.09.13 : 연습문제1-5 추가
22.09.14 : 연습문제6-10 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 선형근사 (2) | 2021.11.24 |
|---|---|
| 미적분학 - 로그함수 미분 (0) | 2021.11.23 |
| 미적분학 - 연쇄 법칙 (0) | 2021.11.09 |
| 미적분학 - 삼각함수 미분 (0) | 2021.11.02 |
| 미적분학 - 곱의 미분과 몫 미분 (0) | 2021.10.29 |
