안녕하세요. 오늘은 지금까지 배웠던 적분의 응용과 관련된 문제들 (넓이, 부피, 평균)과 관련된 연습문제들을 풀어보는 시간을 갖도록 하겠습니다. 문제를 푸시다가 막히거나 모르는 부분이 생기시면 각 주제에 맞는 포스팅을 참조해서 풀어보시길 권장드립니다.
6. 적분 응용 1 (Applications of Integrations 1)
- 미적분학 - 두 곡선 사이의 넓이 (Keyword : 적분과 넓이)
- 미적분학 - 입체 부피 구하기 (Keyword : 적분과 부피)
- 미적분학 - 원통 껍질을 이용한 회전체 부피 구하기 (Keyword : 적분과 회전체의 부피, 원통껍질법)
- 미적분학 - 함수의 평균 (Keyword : 적분과 함수의 평균)
종합연습문제1. 주어진 함수들에 둘러쌓인 영역의 넓이를 구하여라.
(a). $y = x^{2}, y = 4x - x^{2}$
(b). $y = \frac{1}{x}, y = x^{2}, y = 0, x = e$
(c). $y = 1 - 2x^{2}, y = |x|$
(d). $y = \sqrt{x}, y = x^{2}, x = 2$
(e). $y = \sin(\frac{\pi x}{2}), y = x^{2} - 2x$
(a). $y = x^{2}, y = 4x - x^{2}$
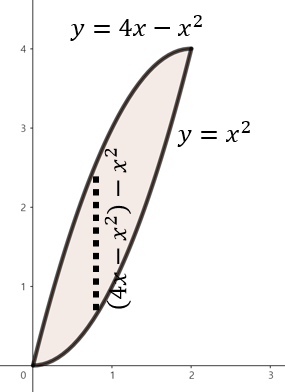
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 직사각형의 높이는 $(4x - x^{2}) - x^{2} = 4x - 2x^{2}$이다. 이제, 구간 $0 \le x \le 2$에서 영역의 넓이를 다음과 같이 구할 수 있다.
$$\begin{align*} A &= \int_{0}^{2} (4x - 2x^{2}) \; dx \\ &= \left[ 2x^{2} - \frac{2}{3}x^{3} \right]_{0}^{2} \\ &= \left( 2 \cdot 2^{2} - \frac{2}{3} \cdot 2^{3} \right) = \frac{8}{3} \end{align*}$$
(b). $y = \frac{1}{x}, y = x^{2}, y = 0, x = e$
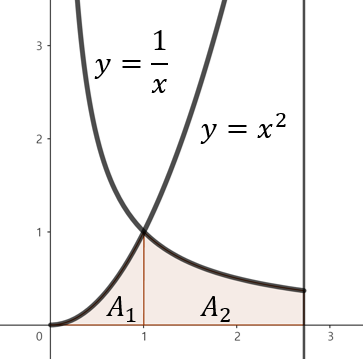
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 주의할 점은 $x = 1$을 기준으로 두 개의 영역에 대한 넓이를 따로 구해야한다. 따라서, 구간 $0 \le x \le 1$에서 직사각형의 높이는 $x^{2}$이고 구간 $1 \le x \le e$에서 직사각형의 높이는 $\frac{1}{x}$이다. 따라서, 전체 구간 $0 \le x \le e$에서 영역의 넓이는 다음과 같이 구할 수 있다.
$$\begin{align*} A &= A_{1} + A_{2} \\ &= \int_{0}^{1} x^{2} \; dx + \int_{1}^{e} \frac{1}{x} \; dx \\ &= \left[ \frac{1}{3}x^{3} \right]_{0}^{1} + \left[ \ln|x| \right]_{1}^{e} \\ &= \frac{1}{3} + 1 = \frac{4}{3} \end{align*}$$
(c). $y = 1 - 2x^{2}, y = |x|$
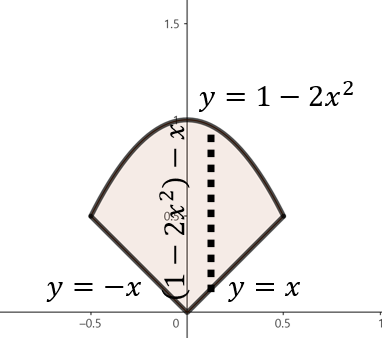
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 직사각형의 높이는 $(1 - 2x^{2}) - x = 1 - x - 2x^{2}$이다. 이제, 구간 $-\frac{1}{2} \le x \le \frac{1}{2}$에서 영역의 넓이를 다음과 같이 구할 수 있다.
$$\begin{align*} A &= 2\int_{0}^{\frac{1}{2}} \left( 1 - x - 2x^{2} \right) \; dx \\ &= 2\left[ x - \frac{1}{2}x^{2} - \frac{2}{3}x^{3} \right]_{0}^{\frac{1}{2}} \\ &= 2 \left( \frac{1}{2} - \frac{1}{2} \cdot \left( \frac{1}{2} \right)^{2} - \frac{2}{3} \cdot \left( \frac{1}{2} \right)^{3} \right) = \frac{7}{12} \end{align*}$$
(d). $y = \sqrt{x}, y = x^{2}, x = 2$
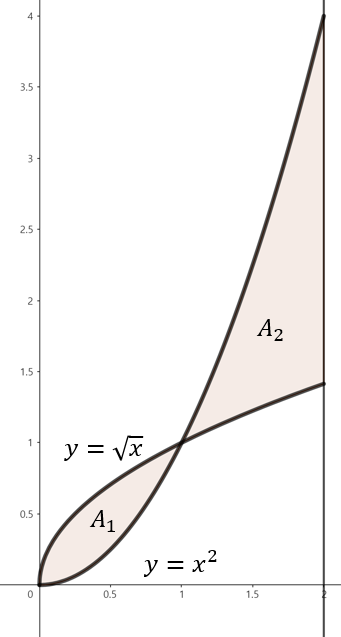
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 주의할 점은 $x = 1$을 기준으로 두 개의 영역에 대한 넓이를 따로 구해야한다. 따라서, 구간 $0 \le x \le 1$에서 직사각형의 높이는 $\sqrt{x} - x^{2}$이고 구간 $1 \le x \le 2$에서 직사각형의 높이는 $x^{2} - \sqrt{x}$이다. 따라서, 전체 구간 $0 \le x \le 2$에서 영역의 넓이는 다음과 같이 구할 수 있다.
$$\begin{align*} A &= A_{1} + A_{2} \\ &= \int_{0}^{1} \left( \sqrt{x} - x^{2} \right) \; dx + \int_{1}^{2} \left( x^{2} - \sqrt{x} \right) \; dx \\ &= \left[ \frac{2}{3}x^{\frac{3}{2}} - \frac{1}{3}x^{3} \right]_{0}^{1} + \left[ \frac{1}{3}x^{3} - \frac{2}{3}x^{\frac{3}{2}} \right]_{1}^{2} \\ &= \left( \frac{2}{3} - \frac{1}{3} \right) + \left[ \left( \frac{1}{3} \cdot 2^{3} - \frac{2}{3} \cdot 2^{\frac{3}{2}} \right) - \left( \frac{1}{3} \cdot 1^{3} - \frac{2}{3} \cdot 1^{\frac{3}{2}} \right) \right] = \frac{10 - 4\sqrt{2}}{3} \end{align*}$$
(e). $y = \sin(\frac{\pi x}{2}), y = x^{2} - 2x$
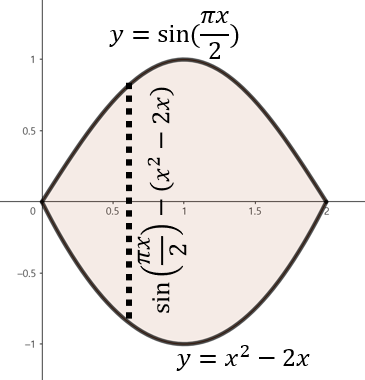
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 직사각형의 높이는 $\sin (\frac{\pi x}{2}) - x^{2} + 2x$이다. 이제, 구간 $0 \le x \le 2$에서 영역의 넓이를 다음과 같이 구할 수 있다.
$$\begin{align*} A &= \int_{0}^{2} \left( \sin(\frac{\pi x}{2}) - x^{2} + 2x \right) \; dx \\ &= \left[ -\frac{1}{3}x^{3} + x^{2} - \frac{2}{\pi} \cos(\frac{\pi x}{2}) \right]_{0}^{2} \\ &= \left( -\frac{1}{3} \cdot 2^{3} + 2^{2} - \frac{2}{\pi} \cos(\pi) \right) + \frac{2}{\pi} \cos(0) = 4 \left( \frac{1}{3} + \frac{1}{\pi} \right)\end{align*}$$
종합연습문제2. 주어진 함수들에 둘러쌓인 영역을 주어진 축을 기준으로 회전했을 때 얻을 수 있는 회전체의 부피를 구하시오.
(a). $y = 2x, y = x^{2}$으로 둘러쌓인 영역을 $x$축 기준으로 회전
(b). $x = 1 + y^{2}, y = x - 3$으로 둘러쌓인 영역을 $y$축 기준으로 회전
(c). $x = 0, x = 9 - y^{2}$으로 둘러쌓인 영역을 $x = -1$을 기준으로 회전
(d). $y = x^{2} + 1, y = 9 - x^{2}$으로 둘러쌓인 영역을 $y = -1$을 기준으로 회전
(a). $y = 2x, y = x^{2}$으로 둘러쌓인 영역을 $x$축 기준으로 회전
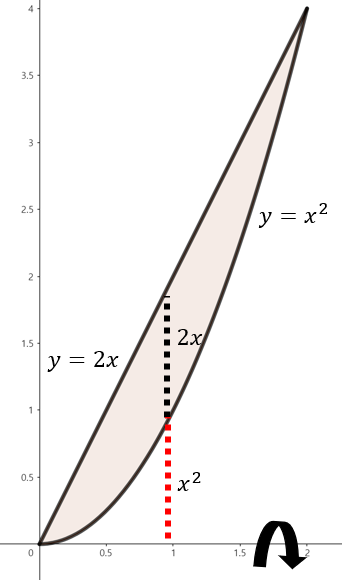
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 $2x$인 원에서 반지름이 $x^{2}$인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $4x^{2} \pi - x^{4} \pi = \left( 4x^{2} - x^{4} \right) \pi$의 넓이를 가진다. 이제, 구간 $0 \le x \le 2$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{2} \pi (4x^{2} - x^{4}) \; dx \\ &= \pi \left[ \frac{4}{3}x^{3} - \frac{1}{5}x^{5} \right]_{0}^{2} \\ &= \pi \left( \frac{4}{3} \cdot 2^{3} - \frac{1}{5} \cdot 2^{5} \right) = \frac{64\pi}{15} \end{align*}$$
(b). $x = 1 + y^{2}, y = x - 3$으로 둘러쌓인 영역을 $y$축 기준으로 회전
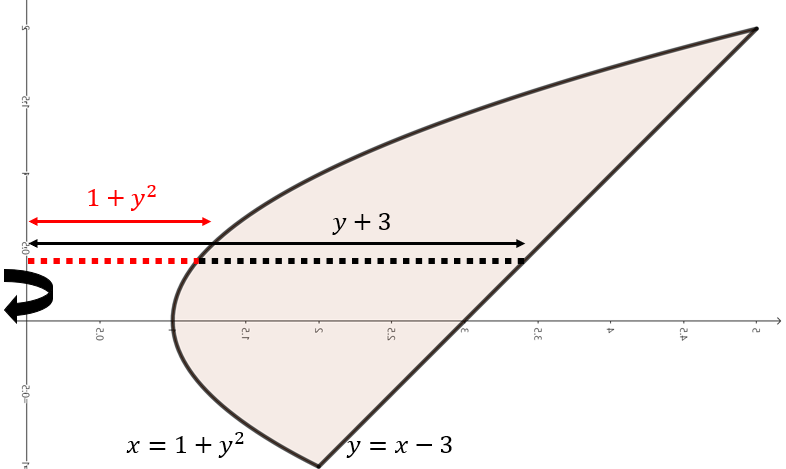
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 $y + 3$인 원에서 반지름이 $1 + y^{2}$인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $(y + 3)^{2} \pi - (1 + y^{2})^{2} \pi = \left( -y^{4} - y^{2} + 6y + 8 \right) \pi$의 넓이를 가진다. 이제, 구간 $-1 \le y \le 2$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{-1}^{2} \pi (-y^{4} - y^{2} + 6y + 8) \; dy \\ &= \pi \left[ -\frac{1}{5}y^{5} - \frac{1}{3}y^{3} + 3y^{2} + 8y \right]_{-1}^{2} \\ &= \pi \left[ \left( -\frac{1}{5} \cdot 2^{5} - \frac{1}{3} \cdot 2^{3} + 3 \cdot 2^{2} + 8 \cdot 2 \right) - \left( -\frac{1}{5} \cdot (-1)^{5} - \frac{1}{3} \cdot (-1)^{3} + 3 \cdot (-1)^{2} + 8 \cdot (-1) \right)\right] = \frac{117\pi}{5} \end{align*}$$
(c). $x = 0, x = 9 - y^{2}$으로 둘러쌓인 영역을 $x = -1$을 기준으로 회전
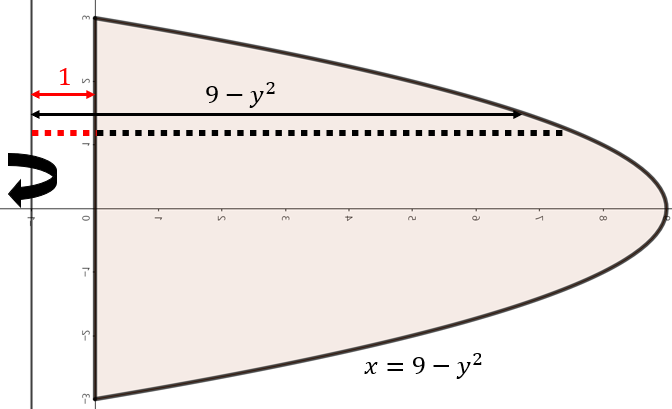
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $x = -1$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 $9 - y^{2}$인 원에서 반지름이 $1$인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $(9 - y^{2})^{2} \pi - \pi = \left( y^{4} - 18y^{2} + 80 \right) \pi$의 넓이를 가진다. 이제, 구간 $-3 \le y \le 3$에서 주어진 영역을 $x = -1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{-3}^{3} \pi (y^{4} - 18y^{2} + 80) \; dy \\ &= 2\int_{0}^{3} \pi (y^{4} - 18y^{2} + 80) \; dy \\ &= 2\pi \left[ \frac{1}{5}y^{5} - 6y^{3} + 80y \right]_{0}^{3} \\ &= 2\pi \left( \frac{1}{5} \cdot 3^{5} - 6 \cdot 3^{3} + 80 \cdot 3 \right) = \frac{1266\pi}{5} \end{align*}$$
(d). $y = x^{2} + 1, y = 9 - x^{2}$으로 둘러쌓인 영역을 $y = -1$을 기준으로 회전
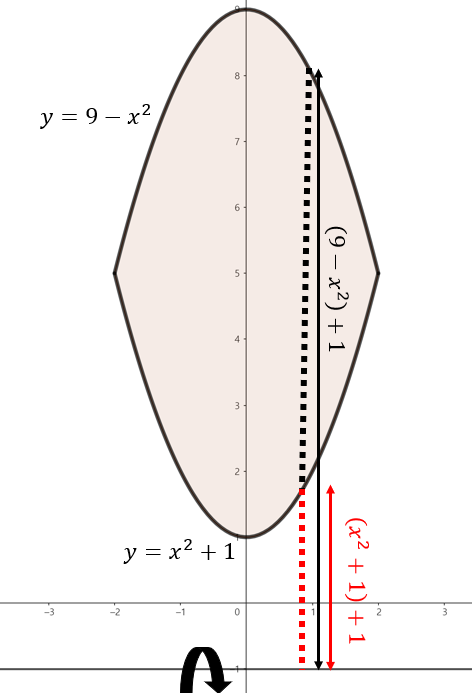
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y = -1$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 $(9 - x^{2}) + 1 = 10 - x^{2}$인 원에서 반지름이 $(x^{2} + 1) + 1 = x^{2} + 2$인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $(10 - x^{2})^{2} \pi - (x^{2} + 2)^{2} \pi = \left( -24x^{2} + 96 \right) \pi$의 넓이를 가진다. 이제, 구간 $-2 \le x \le 2$에서 주어진 영역을 $y = -1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{-2}^{2} \pi (-24x^{2} + 96) \; dx \\ &= 2\int_{0}^{2} \pi (-24x^{2} + 96) \; dx \\ &= 2\pi \left[ -8x^{3} + 96x \right]_{0}^{2} \\ &= 2\pi \left( -8 \cdot 2^{3} + 96 \cdot 2 \right) = 256\pi \end{align*}$$
종합연습문제3. $y = x$와 $y = x^{2}$으로 둘러쌓인 영역을 주어진 각 축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 구하여라.
(a). $x$축 기준으로 회전
(b). $y$축 기준으로 회전
(c). $y = 2$ 기준으로 회전
(a). $x$축 기준으로 회전
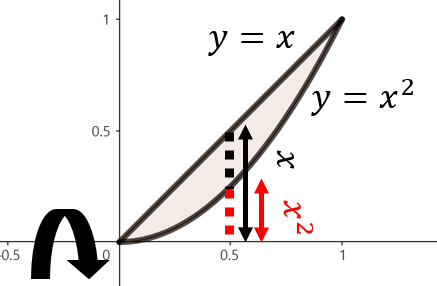
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 $x$인 원에서 반지름이 $x^{2}$인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $\left( x^{2} - x^{4} \right) \pi$의 넓이를 가진다. 이제, 구간 $0 \le x \le 1$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} \pi (x^{2} - x^{4}) \; dx \\ &= \pi \left[ \frac{1}{3}x^{3} - \frac{1}{5}x^{5} \right]_{0}^{1} \\ &= \pi \left( \frac{1}{3} - \frac{1}{5} \right) = \frac{2}{15}\pi \end{align*}$$
(b). $y$축 기준으로 회전
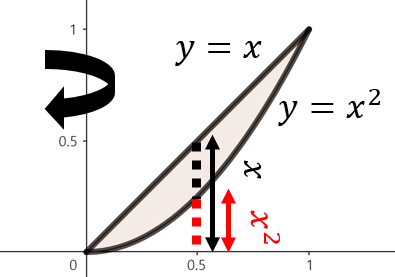
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $x - x^{2}$이다. 이제, 구간 $0 \le x \le 1$에서 주어진 영역을 $y$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} 2\pi x \left( x - x^{2} \right) \; dx \\ &= 2\pi \int_{0}^{1} \left( x^{2} - x^{3} \right) \; dx \\ &= 2\pi \left[ \frac{1}{3}x^{3} - \frac{1}{4}x^{4} \right]_{0}^{1} \\ &= 2\pi \left( \frac{1}{3} - \frac{1}{4} \right) = \frac{\pi}{6} \end{align*}$$
(c). $y = 2$ 기준으로 회전
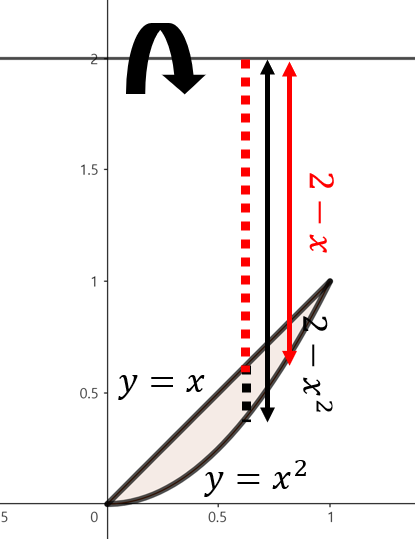
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y = 2$을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 $2 - x^{2}$인 원에서 반지름이 $2 - x$인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $(2 - x^{2})^{2} \pi - (2 - x)^{2} \pi = \left( x^{4} - 5x^{2} + 4 \right) \pi$의 넓이를 가진다. 이제, 구간 $0 \le x \le 1$에서 주어진 영역을 $y = 2$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} \pi (x^{4} - 5x^{2} + 4) \; dx \\ &= \pi \left[ \frac{1}{5}x^{5} - \frac{5}{3}x^{3} + 4x \right]_{0}^{1} \\ &= \pi \left( \frac{1}{5} - \frac{5}{3} + 4 \right) = \frac{38}{15}\pi \end{align*}$$
종합연습문제4. 주어진 적분이 어떤 회전체의 부피를 구하는 지 설명하라.
(a). $\int_{0}^{\frac{\pi}{2}} 2\pi x \cos(x) \; dx$
(b). $\int_{0}^{\frac{\pi}{2}} 2\pi \cos^{2}(x) \; dx$
(c). $\int_{0}^{\pi} \pi (2 - \sin(x))^{2} \; dx$
(a). $\int_{0}^{\frac{\pi}{2}} 2\pi x \cos(x) \; dx$
$y = \cos(x), x = \frac{\pi}{2}, y = 0$으로 둘러쌓인 영역을 $y$축을 중심으로 회전한 회전체의 부피를 의미한다.
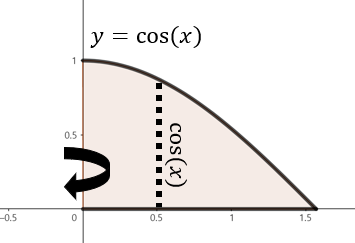
(b). $\int_{0}^{\frac{\pi}{2}} 2\pi \cos^{2}(x) \; dx$
$y = \cos(x), x = -\frac{\pi}{2}, x = \frac{\pi}{2}, y = 0$으로 둘러쌓인 영역을 $x$축을 중심으로 회전한 회전체의 부피를 의미한다.
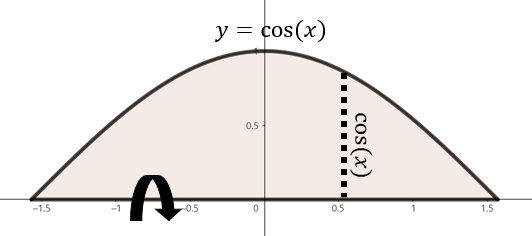
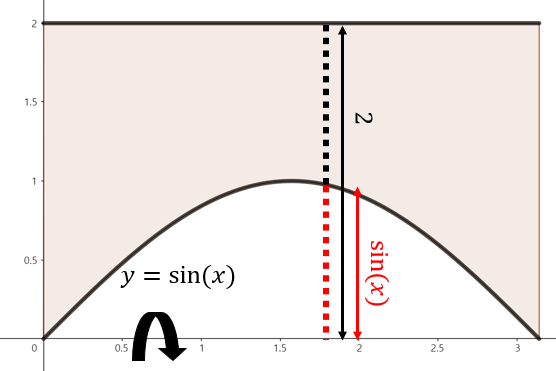
(c). $\int_{0}^{\pi} \pi (2 - \sin(x))^{2} \; dx$
$y = \sin(x), x = 0, x = \pi, y = 2$으로 둘러쌓인 영역을 $x$축을 중심으로 회전한 회전체의 부피를 의미한다.
종합연습문제5. 구간 $[0, 10]$에서 함수 $f(t) = t\sin(t^{2})$의 평균을 구하여라.
$$\begin{align*} A &= \frac{1}{10 - 0} \int_{0}^{10} t\sin(t^{2}) \; dt \end{align*}$$
$t^{2} = u$라고 하자.
$$2t dt = du \rightarrow dt = \frac{1}{2t} du$$
그리고 윗끝과 아래끝은 아래와 같다.
$$\begin{cases} &t = 10 \rightarrow u = 100 \\ &x = 0 \rightarrow u = 0 \end{cases}$$
이제 주어진 정적분을 치환적분을 이용해서 해결한다.
$$\begin{align*} A &= \frac{1}{10} \int_{0}^{10} t\sin(t^{2}) \; dt \\ &= \frac{1}{10} \int_{0}^{100} \frac{1}{2} \sin(u) \; du \\ &= \frac{1}{20} \left[ -\cos(u) \right]_{0}^{100} \\ &= \frac{1}{20} \left( 1 - \cos(100) \right) \end{align*}$$
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 적분 연습문제 (0) | 2022.11.30 |
|---|---|
| 미적분학 - 미분 규칙 연습문제 (0) | 2022.09.22 |
| 미적분학 - 쌍곡함수 (0) | 2022.09.10 |
| 미적분학 - 목차 (0) | 2022.08.03 |
| 미적분학 - 발산 정리 (0) | 2022.08.02 |
안녕하세요. 오늘은 지금까지 배웠던 적분의 응용과 관련된 문제들 (넓이, 부피, 평균)과 관련된 연습문제들을 풀어보는 시간을 갖도록 하겠습니다. 문제를 푸시다가 막히거나 모르는 부분이 생기시면 각 주제에 맞는 포스팅을 참조해서 풀어보시길 권장드립니다.
6. 적분 응용 1 (Applications of Integrations 1)
- 미적분학 - 두 곡선 사이의 넓이 (Keyword : 적분과 넓이)
- 미적분학 - 입체 부피 구하기 (Keyword : 적분과 부피)
- 미적분학 - 원통 껍질을 이용한 회전체 부피 구하기 (Keyword : 적분과 회전체의 부피, 원통껍질법)
- 미적분학 - 함수의 평균 (Keyword : 적분과 함수의 평균)
종합연습문제1. 주어진 함수들에 둘러쌓인 영역의 넓이를 구하여라.
(a). y=x2,y=4x−x2
(b). y=1x,y=x2,y=0,x=e
(c). y=1−2x2,y=|x|
(d). y=√x,y=x2,x=2
(e). y=sin(πx2),y=x2−2x
(a). y=x2,y=4x−x2

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 x에서 직사각형의 높이는 (4x−x2)−x2=4x−2x2이다. 이제, 구간 0≤x≤2에서 영역의 넓이를 다음과 같이 구할 수 있다.
A=∫20(4x−2x2)dx=[2x2−23x3]20=(2⋅22−23⋅23)=83
(b). y=1x,y=x2,y=0,x=e

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 주의할 점은 x=1을 기준으로 두 개의 영역에 대한 넓이를 따로 구해야한다. 따라서, 구간 0≤x≤1에서 직사각형의 높이는 x2이고 구간 1≤x≤e에서 직사각형의 높이는 1x이다. 따라서, 전체 구간 0≤x≤e에서 영역의 넓이는 다음과 같이 구할 수 있다.
A=A1+A2=∫10x2dx+∫e11xdx=[13x3]10+[ln|x|]e1=13+1=43
(c). y=1−2x2,y=|x|

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 x에서 직사각형의 높이는 (1−2x2)−x=1−x−2x2이다. 이제, 구간 −12≤x≤12에서 영역의 넓이를 다음과 같이 구할 수 있다.
A=2∫120(1−x−2x2)dx=2[x−12x2−23x3]120=2(12−12⋅(12)2−23⋅(12)3)=712
(d). y=√x,y=x2,x=2

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 주의할 점은 x=1을 기준으로 두 개의 영역에 대한 넓이를 따로 구해야한다. 따라서, 구간 0≤x≤1에서 직사각형의 높이는 √x−x2이고 구간 1≤x≤2에서 직사각형의 높이는 x2−√x이다. 따라서, 전체 구간 0≤x≤2에서 영역의 넓이는 다음과 같이 구할 수 있다.
A=A1+A2=∫10(√x−x2)dx+∫21(x2−√x)dx=[23x32−13x3]10+[13x3−23x32]21=(23−13)+[(13⋅23−23⋅232)−(13⋅13−23⋅132)]=10−4√23
(e). y=sin(πx2),y=x2−2x

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 x에서 직사각형의 높이는 sin(πx2)−x2+2x이다. 이제, 구간 0≤x≤2에서 영역의 넓이를 다음과 같이 구할 수 있다.
A=∫20(sin(πx2)−x2+2x)dx=[−13x3+x2−2πcos(πx2)]20=(−13⋅23+22−2πcos(π))+2πcos(0)=4(13+1π)
종합연습문제2. 주어진 함수들에 둘러쌓인 영역을 주어진 축을 기준으로 회전했을 때 얻을 수 있는 회전체의 부피를 구하시오.
(a). y=2x,y=x2으로 둘러쌓인 영역을 x축 기준으로 회전
(b). x=1+y2,y=x−3으로 둘러쌓인 영역을 y축 기준으로 회전
(c). x=0,x=9−y2으로 둘러쌓인 영역을 x=−1을 기준으로 회전
(d). y=x2+1,y=9−x2으로 둘러쌓인 영역을 y=−1을 기준으로 회전
(a). y=2x,y=x2으로 둘러쌓인 영역을 x축 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 x에서 x축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 2x인 원에서 반지름이 x2인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $4x^{2} \pi - x^{4} \pi = \left( 4x^{2} - x^{4} \right) \pi의넓이를가진다.이제,구간0 \le x \le 2에서주어진영역을x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
V=∫20π(4x2−x4)dx=π[43x3−15x5]20=π(43⋅23−15⋅25)=64π15
(b). x=1+y2,y=x−3으로 둘러쌓인 영역을 y축 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 y에서 y축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 y+3인 원에서 반지름이 1+y2인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $(y + 3)^{2} \pi - (1 + y^{2})^{2} \pi = \left( -y^{4} - y^{2} + 6y + 8 \right) \pi의넓이를가진다.이제,구간-1 \le y \le 2에서주어진영역을x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
V=∫2−1π(−y4−y2+6y+8)dy=π[−15y5−13y3+3y2+8y]2−1=π[(−15⋅25−13⋅23+3⋅22+8⋅2)−(−15⋅(−1)5−13⋅(−1)3+3⋅(−1)2+8⋅(−1))]=117π5
(c). x=0,x=9−y2으로 둘러쌓인 영역을 x=−1을 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 y에서 x=−1축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 9−y2인 원에서 반지름이 1인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $(9 - y^{2})^{2} \pi - \pi = \left( y^{4} - 18y^{2} + 80 \right) \pi의넓이를가진다.이제,구간-3 \le y \le 3에서주어진영역을x = -1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
V=∫3−3π(y4−18y2+80)dy=2∫30π(y4−18y2+80)dy=2π[15y5−6y3+80y]30=2π(15⋅35−6⋅33+80⋅3)=1266π5
(d). y=x2+1,y=9−x2으로 둘러쌓인 영역을 y=−1을 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 x에서 y=−1축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 (9−x2)+1=10−x2인 원에서 반지름이 (x2+1)+1=x2+2인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $(10 - x^{2})^{2} \pi - (x^{2} + 2)^{2} \pi = \left( -24x^{2} + 96 \right) \pi의넓이를가진다.이제,구간-2 \le x \le 2에서주어진영역을y = -1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
V=∫2−2π(−24x2+96)dx=2∫20π(−24x2+96)dx=2π[−8x3+96x]20=2π(−8⋅23+96⋅2)=256π
종합연습문제3. y=x와 y=x2으로 둘러쌓인 영역을 주어진 각 축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 구하여라.
(a). x축 기준으로 회전
(b). y축 기준으로 회전
(c). y=2 기준으로 회전
(a). x축 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 x에서 x축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 x인 원에서 반지름이 x2인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $\left( x^{2} - x^{4} \right) \pi의넓이를가진다.이제,구간0 \le x \le 1에서주어진영역을x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
V=∫10π(x2−x4)dx=π[13x3−15x5]10=π(13−15)=215π
(b). y축 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 x에서 y축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 x−x2이다. 이제, 구간 0≤x≤1에서 주어진 영역을 y축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
V=∫102πx(x−x2)dx=2π∫10(x2−x3)dx=2π[13x3−14x4]10=2π(13−14)=π6
(c). y=2 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 x에서 y=2을 기준으로 회전했을 때 얻을 수 있는 회전체 단면은 반지름이 2−x2인 원에서 반지름이 2−x인 원을 뺀 것과 동일하다. 따라서, 해당 구간의 단면은 $(2 - x^{2})^{2} \pi - (2 - x)^{2} \pi = \left( x^{4} - 5x^{2} + 4 \right) \pi의넓이를가진다.이제,구간0 \le x \le 1에서주어진영역을y = 2$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
V=∫10π(x4−5x2+4)dx=π[15x5−53x3+4x]10=π(15−53+4)=3815π
종합연습문제4. 주어진 적분이 어떤 회전체의 부피를 구하는 지 설명하라.
(a). ∫π202πxcos(x)dx
(b). ∫π202πcos2(x)dx
(c). ∫π0π(2−sin(x))2dx
(a). ∫π202πxcos(x)dx
y=cos(x),x=π2,y=0으로 둘러쌓인 영역을 y축을 중심으로 회전한 회전체의 부피를 의미한다.

(b). ∫π202πcos2(x)dx
y=cos(x),x=−π2,x=π2,y=0으로 둘러쌓인 영역을 x축을 중심으로 회전한 회전체의 부피를 의미한다.

(c). ∫π0π(2−sin(x))2dx
y=sin(x),x=0,x=π,y=2으로 둘러쌓인 영역을 x축을 중심으로 회전한 회전체의 부피를 의미한다.

종합연습문제5. 구간 [0,10]에서 함수 f(t)=tsin(t2)의 평균을 구하여라.
A=110−0∫100tsin(t2)dt
t2=u라고 하자.
2tdt=du→dt=12tdu
그리고 윗끝과 아래끝은 아래와 같다.
{t=10→u=100x=0→u=0
이제 주어진 정적분을 치환적분을 이용해서 해결한다.
A=110∫100tsin(t2)dt=110∫100012sin(u)du=120[−cos(u)]1000=120(1−cos(100))
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 적분 연습문제 (0) | 2022.11.30 |
|---|---|
| 미적분학 - 미분 규칙 연습문제 (0) | 2022.09.22 |
| 미적분학 - 쌍곡함수 (0) | 2022.09.10 |
| 미적분학 - 목차 (0) | 2022.08.03 |
| 미적분학 - 발산 정리 (0) | 2022.08.02 |
