안녕하세요. 지난 포스팅의 미적분학 - 입체 부피 구하기에서는 $x$축 또는 $y$축을 중심으로 회전한 회전체의 부피를 구하는 방법에 대해서 알아보았습니다. 오늘은 중간이 비어있는 형태의 회전체의 부피를 구하는 방법인 실린더 방법(method of cylinder shell)에 대해서 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.

일단, 위의 그림과 같이 $y = 2x^{2} - x^{3}$과 $y = 0$으로 둘러쌓인 영역이 있다고 가정하겠습니다. 그리고 이 영역을 $y$축을 중심으로 회전시켰을 때 얻는 회전체의 부피를 고려해보도록 하겠습니다. 지금까지 저희가 보았던 부피를 구하기 위해서는 $y$축을 중심으로 회전하기 때문에 주어진 식을 $y$에 대한 식으로 변형해야합니다. 물론 지난 포스팅의 연습문제들처럼 쉽게 변형할 수 있는 경우도 있지만 위 그림은 쉽게 바꾸기 어려운 형태입니다. 따라서, 이러한 형태를 가지는 회전체의 부피를 계산하기 위해서 실린더 방법을 생각할 수 있습니다.

실린더 방법은 굉장히 단순합니다. 위 그림과 같이 가장 바깥 실린더의 반지름을 $r_{1}$, 안에 있는 실린더의 반지름을 $r_{1}$, 높이를 $h$라고 했을 때 실린더의 부피는 아래와 같습니다. 이때, $r = \frac{r_{1} + r_{2}}{2}$로 두 반지름의 평균이라고 하겠습니다.
$$\begin{align*} V &= V_{2} - V_{1} = \pi r_{2}^{2}h - \pi r_{1}^{2}h = \pi \left(r_{2}^{2} - r_{1}^{2}\right)h \\ &= \pi\left(r_{2} + r_{1}\right)\left(r_{2} - r_{1}\right)h = 2\pi \frac{r_{1} + r_{2}}{2} h \left(r_{2} - r_{1}\right) \\ & = 2\pi rh \Delta r\end{align*}$$
여기서 각 요소는 $2\pi r$은 원둘레 (circumference), $h$는 높이 (height) , $\Delta x$는 실린더 두께 (thickness)입니다.

이제는 조금 더 일반적인 상황을 고려해보도록 하겠습니다. $y = f(x)$와 $y = 0, x = a, x = b$으로 둘러쌓인 영역을 $y$축을 기준으로 회전시켰을 때 얻는 회전체의 부피를 구해보도록 하죠.

지난 포스팅과 마찬가지로 영역을 $n$개의 등구간으로 만들어줍니다. 각 구간을 $[x_{i - 1}, x_{i}]$라고 했을 때, 각 구간의 너비는 $\Delta x$, 그리고 표본점을 중간점으로 했을 때 $\bar{x}_{i}$를 $i$번째 표본점이라고 하겠습니다. 따라서, $i$번째 실린더의 부피는 $V_{i} = \left(2 \pi \bar{x}_{i}\right) \left[f(\bar{x}_{i})\right] \Delta x$이기 때문에 근사된 부피는 아래와 같습니다.
$$V \approx \sum_{i = 1}^{n} V_{i} = \sum_{i = 1}^{n} \left(2 \pi \bar{x}_{i}\right) \left[f(\bar{x}_{i})\right] \Delta x$$
그리고 이 식에 극한을 취하면 저희가 원하는 결과를 얻을 수 있습니다.
$$V = \lim_{n \rightarrow \infty} \sum_{i = 1}^{n} V_{i} = \lim_{n \rightarrow \infty} \sum_{i = 1}^{n} \left(2 \pi \bar{x}_{i}\right) \left[f(\bar{x}_{i})\right] \Delta x = \int_{a}^{b} 2\pi x f(x) \; dx$$
이제 드디어 저희가 처음에 구하고자 했던 회전체의 부피를 구할 수 있습니다. $y = 2x^{2} - x^{3}$이고 $y = 0, x = 0, x = 2$로 둘러쌓인 영역을 $y$축을 중심으로 회전했을 때 얻는 회전체의 부피는 아래와 같습니다.
$$\begin{align*} V &= \int_{0}^{2} 2\pi x \left(2x^{2} - x^{3}\right) \; dx \\ &= 2\pi \int_{0}^{2} \left(2x^{3} - x^{4}\right) \; dx \\ &= 2\pi \left[\frac{1}{2}x^{4} - \frac{1}{5}x^{5}\right]_{0}^{2} = \frac{16}{5} \pi\end{align*}$$
예제1. $y = x, y = x^{2}$로 둘러쌓은 영역을 $y$축을 중심으로 회전시켰을 때 얻는 회전체의 부피를 구하여라.

$x = x^{2}$이라고 했을 때, 두 곡선은 $x = 0, x = 1$에서 만난다. 그리고, $x$를 반지름이라고 할 때, 실린더의 높이는 두 곡선의 높이차와 동일하기 때문에 $h = x - x^{2}$이다. 따라서, 회전체의 부피는 아래와 같다.
$$\begin{align*} V = \int_{0}^{1} 2\pi x \left(x - x^{2}\right) \; dx \\ &= 2\pi \int_{0}^{1} \left(x^{2} - x^{3}\right) \; dx \\ &= 2 \pi \left[\frac{1}{3}x^{3} - \frac{1}{4} x^{4}\right]_{0}^{1} = 2 \pi \frac{1}{12} = \frac{1}{6}\pi \end{align*}$$
연습문제1. 주어진 함수들에 둘러쌓인 영역을 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체의 부피를 구하여라.
(a). $y = \frac{1}{x}, y = 0, x = 1, x = 2$
(b). $y = x^{2}, y = 0, x = 1$
(c). $y = e^{-x^{2}}, y = 0, x = 0, x = 1$
(d). $y = 3 + 2x - x^{2}, x + y = 3$
(e). $y = 4(x - 2)^{2}, y = x^{2} - 4x + 7$
(a). $y = \frac{1}{x}, y = 0, x = 1, x = 2$

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $\frac{1}{x}$이다. 이제, 구간 $1 \le x \le 2$에서 주어진 영역을 $y$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{1}^{2} 2\pi x \frac{1}{x} \; dx \\ &= \int_{1}^{2} 2\pi \; dx \\ &= 2\pi \left[ x \right]_{1}^{2} \\ &= 2\pi \left( 2 - 1 \right) = 2\pi \end{align*}$$
(b). $y = x^{2}, y = 0, x = 1$

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $x^{2}$이다. 이제, 구간 $0 \le x \le 1$에서 주어진 영역을 $y$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} 2\pi x x^{2} \; dx \\ &= \int_{0}^{1} 2\pi x^{3} \; dx \\ &= 2\pi \left[ \frac{1}{4} x^{4} \right]_{0}^{1} \\ &= 2\pi \left( \frac{1}{4} \right) = \frac{\pi}{2} \end{align*}$$
(c). $y = e^{-x^{2}}, y = 0, x = 0, x = 1$

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $e^{-x^{2}}$이다. 이제, 구간 $0 \le x \le 1$에서 주어진 영역을 $y$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} 2\pi x e^{-x^{2}} \; dx \\ &= 2 \pi \int_{0}^{1} xe^{-x^{2}} \; dx \end{align*}$$
$-x^{2} = u$라고 하자.
$$-2x dt = du \rightarrow dt = -\frac{1}{2x} du$$
그리고 윗끝과 아래끝은 아래와 같다.
$$\begin{cases} &x= 1 \rightarrow u = -1 \\ &x = 0 \rightarrow u = 0 \end{cases}$$
이제 주어진 정적분을 치환적분을 이용해서 해결한다.
$$\begin{align*} 2\pi \int_{0}^{1} xe^{-x^{2}} \; dx &= 2\pi \int_{-1}^{0} xe^{u} \; \left( -\frac{1}{2x} du \right) \\ &= 2\pi \cdot \frac{1}{2} \int_{-1}^{0} e^{u} \; du \\ &= \pi \left[ e^{u} \right]_{-1}^{0} = \pi \left( 1 - \frac{1}{e} \right)\end{align*}$$
(d). $y = 3 + 2x - x^{2}, x + y = 3$

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $\left( 3 + 2x - x^{2} \right) - \left( -x + 3 \right) = 3x - x^{2}$이다. 이제, 구간 $0 \le x \le 3$에서 주어진 영역을 $y$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{3} 2\pi x \left( 3x - x^{2} \right) \; dx \\ &= 2\pi \int_{0}^{3} \left( 3x^{2} - x^{3} \right) \; dx \\ &= 2\pi \left[ x^{3} - \frac{1}{4}x^{4} \right]_{0}^{3} \\ &= 2\pi \left( 3^{3} - \frac{1}{4}3^{4} \right) = \frac{27\pi}{2} \end{align*}$$
(e). $y = 4(x - 2)^{2}, y = x^{2} - 4x + 7$
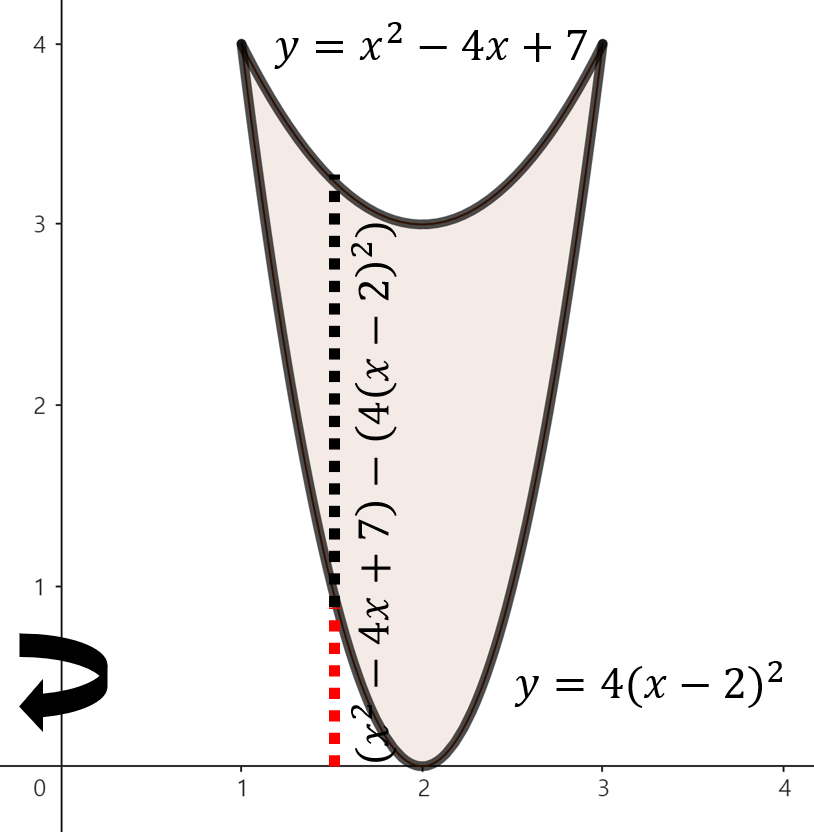
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $\left( x^{2} - 4x + 7 \right) - \left( 4(x - 2)^{2} \right) = -3x^{2} + 12x - 9$이다. 이제, 구간 $1 \le x \le 3$에서 주어진 영역을 $y$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{1}^{3} 2\pi x \left( -3x^{2} + 12x - 9 \right) \; dx \\ &= 2\pi \int_{1}^{3} \left( -3x^{3} + 12x^{2} - 9x \right) \; dx \\ &= 2\pi \left[ -\frac{3}{4}x^{4} + 4 x^{3} - \frac{9}{2}x^{2} \right]_{1}^{3} \\ &= 2\pi \left[ \left( -\frac{3}{4} \cdot 3^{4} + 4 \cdot 3^{3} - \frac{9}{2} \cdot 3^{2} \right) - \left( -\frac{3}{4} \cdot 1^{4} + 4 \cdot 1^{3} - \frac{9}{2} \cdot 1^{2} \right) \right] = 16\pi \end{align*}$$
연습문제2. 주어진 함수들에 둘러쌓인 영역을 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체의 부피를 구하여라.
(a). $x = 1 + y^{2}, x = 0, y = 1, y = 2$
(b). $x = \sqrt{y}, x = 0, y = 1$
(c). $y = x^{3}, y = 8, x = 0$
(d). $x = 4y^{2} - y^{3}, x = 0$
(e). $x = 1 + (y - 2)^{2}, x = 2$
(a). $x = 1 + y^{2}, x = 0, y = 1, y = 2$

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $1 + y^{2}$이다. 이제, 구간 $1 \le y \le 2$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{1}^{2} 2\pi y \left( 1 + y^{2} \right) \; dy \\ &= 2\pi \int_{1}^{2} \left( y + y^{3} \right) \; dy \\ &= 2\pi \left[ \frac{1}{2}y^{2} + \frac{1}{4} y^{4} \right]_{1}^{2} \\ &= 2\pi \left[ \left( \frac{1}{2} \cdot 2^{2} + \frac{1}{4} \cdot 2^{4} \right) - \left( \frac{1}{2} \cdot 1^{2} + \frac{1}{4} \cdot 1^{4} \right) \right] = \frac{21\pi}{2} \end{align*}$$
(b). $x = \sqrt{y}, x = 0, y = 1$

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $\sqrt{y}$이다. 이제, 구간 $0 \le y \le 1$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} 2\pi y \sqrt{y} \; dy \\ &= 2\pi \int_{0}^{1} y^{\frac{3}{2}} \; dy \\ &= 2\pi \left[ \frac{2}{5}y^{\frac{5}{2}} \right]_{0}^{1} \\ &= 2\pi \left[ \left( \frac{2}{5} \cdot 1^{\frac{5}{2}} \right) - \left( \frac{2}{5} \cdot 0^{\frac{5}{2}} \right) \right] = \frac{4\pi}{5} \end{align*}$$
(c). $y = x^{3}, y = 8, x = 0$

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $y^{\frac{1}{3}}이다. 이제, 구간 $0 \le y \le 8$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{8} 2\pi y y^{\frac{1}{3}} \; dy \\ &= 2\pi \int_{0}^{8} y^{\frac{4}{3}} \; dy \\ &= 2\pi \left[ \frac{3}{7}y^{\frac{7}{3}} \right]_{0}^{8} \\ &= 2\pi \left[ \left( \frac{3}{7} \cdot 8^{\frac{7}{3}} \right) - \left( \frac{3}{7} \cdot 0^{\frac{7}{3}} \right) \right] = \frac{384\pi}{7} \end{align*}$$
(d). $x = 4y^{2} - y^{3}, x = 0$
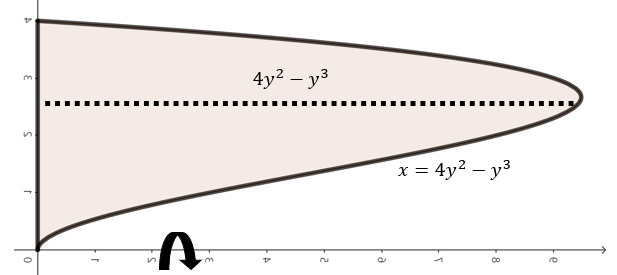
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $4y^{2} - y^{3}이다. 이제, 구간 $0 \le y \le 4$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{4} 2\pi y \left( 4y^{2} - y^{3} \right) \; dy \\ &= 2\pi \int_{0}^{4} \left( 4y^{3} - y^{4} \right) \; dy \\ &= 2\pi \left[ y^{4} - \frac{1}{5}y^{5} \right]_{0}^{4} \\ &= 2\pi \left[ \left( 4^{4} - \frac{1}{5} \cdot 4^{5} \right) \right] = \frac{512\pi}{5} \end{align*}$$
(e). $x = 1 + (y - 2)^{2}, x = 2$

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $2 - (1 + (y - 2)^{2}) = -y^{2} + 4y - 3$이다. 이제, 구간 $1 \le y \le 3$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{1}^{3} 2\pi y \left( -y^{2} + 4y - 3 \right) \; dy \\ &= 2\pi \int_{1}^{3} \left( -y^{3} + 4y^{2} - 3y \right) \; dy \\ &= 2\pi \left[ -\frac{1}{4}y^{4} + \frac{4}{3}y^{3} - \frac{3}{2}y^{2} \right]_{1}^{3} \\ &= 2\pi \left[ \left( -\frac{1}{4} \cdot 3^{4} + \frac{4}{3} \cdot 3^{3} - \frac{3}{2} \cdot 3^{2} \right) - \left( -\frac{1}{4} \cdot 1^{4} + \frac{4}{3} \cdot 1^{3} - \frac{3}{2} \cdot 1^{2} \right) \right] = \frac{16\pi}{3} \end{align*}$$
연습문제3. 주어진 함수들에 둘러쌓인 영역을 주어진 축을 기준으로 회전했을 때 얻을 수 있는 회전체의 부피를 구하여라.
(a). $y = \sqrt{x}, y = 0, x = 1$로 둘러쌓인 영역을 $x = -1$을 기준으로 회전
(b). $y =4x - x^{2}, y = 3$로 둘러쌓인 영역을 $x = 1$을 기준으로 회전
(c). $y = x^{2}, y = 2 - x^{2}$로 둘러쌓인 영역을 $x = 1$을 기준으로 회전
(d). $y = x^{3}, y = 0, x = 1$로 둘러쌓인 영역을 $y = 1$을 기준으로 회전
(e). $y = x^{2}, x = y^{2}$로 둘러쌓인 영역을 $y = -1$을 기준으로 회전
(a). $y = \sqrt{x}, y = 0, x = 1$로 둘러쌓인 영역을 $x = -1$을 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $x = -1$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $\sqrt{x}$이다. 이제, 구간 $0 \le x \le 1$에서 주어진 영역을 $x = -1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} 2\pi (x + 1) \sqrt{x} \; dx \\ &= 2\pi \int_{0}^{1} \left( x^{\frac{3}{2}} + x^{\frac{1}{2}} \right) \; dx \\ &= 2\pi \left[ \frac{2}{5}x^{\frac{5}{2}} + \frac{2}{3}x^{\frac{3}{2}}\right]_{0}^{1} \\ &= 2\pi \cdot \left( \frac{2}{5} + \frac{2}{3} \right) = \frac{32\pi}{15} \end{align*}$$
(b). $y =4x - x^{2}, y = 3$로 둘러쌓인 영역을 $x = 1$을 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $x = 1$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $4x - x^{2}$이다. 이제, 구간 $1 \le x \le 3$에서 주어진 영역을 $x = 1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{1}^{3} 2\pi (x - 1) \left( 4x - x^{2} \right) \; dx \\ &= 2\pi \int_{1}^{3} \left( -x^{3} + 5x^{2} - 4x \right) \; dx \\ &= 2\pi \left[ -\frac{1}{4}x^{4} + \frac{5}{3}x^{3} - 2x^{2} \right]_{1}^{3} \\ &= 2\pi \left[ \left( -\frac{1}{4} \cdot 3^{4} + \frac{5}{3} \cdot 3^{3} - 2 \cdot 3^{2} \right) - \left( -\frac{1}{4} \cdot 1^{4} + \frac{5}{3} \cdot 1^{3} - 2 \cdot 1^{2} \right) \right] = \frac{44\pi}{3} \end{align*}$$
(c). $y = x^{2}, y = 2 - x^{2}$로 둘러쌓인 영역을 $x = 1$을 기준으로 회전
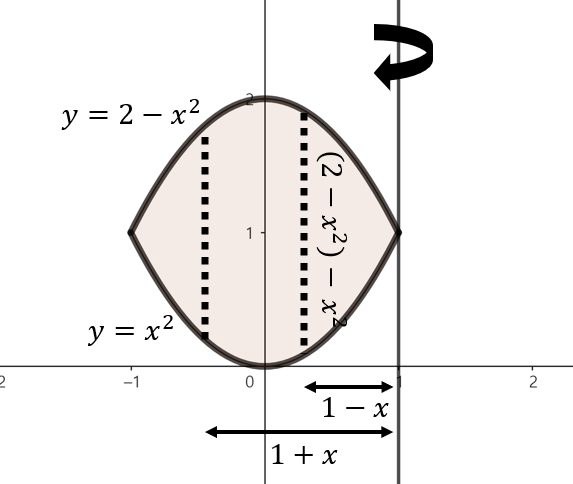
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $x = 1$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $(2 - x^{2}) - x^{2} = 2 - 2x^{2}$이다. 이제, 구간 $-1 \le x \le 1$에서 주어진 영역을 $x = 1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} 2\pi (1 - x) \left( 2 - 2x^{2} \right) \; dx + \int_{-1}^{0} 2\pi (1 + x) \left( 2 - 2x^{2} \right) \; dx \\ &= 2\pi \int_{0}^{1} \left( 2x^{3} - 2x^{2} - 2x + 2 \right) \; dx + 2\pi \int_{-1}^{0} \left( -2x^{3} - 2x^{2} + 2x + 2 \right) \; dx \\ &= 2\pi \left[ \frac{1}{2}x^{4} - \frac{2}{3}x^{3} - x^{2} + 2x \right]_{0}^{1} + 2\pi \left[ -\frac{1}{2}x^{4} - \frac{2}{3}x^{3} + x^{2} + 2x \right]_{-1}^{0} \\ &= 2\pi \cdot \frac{5}{6} + 2\pi \cdot \frac{5}{6} = \frac{10\pi}{3}\end{align*}$$
(d). $y = x^{3}, y = 0, x = 1$로 둘러쌓인 영역을 $y = 1$을 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $y = 1$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $1 - y^{\frac{1}{3}}$이다. 이제, 구간 $0 \le y \le 1$에서 주어진 영역을 $y = 1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} 2\pi (1 - y) \left( 1 - y^{\frac{1}{3}} \right) \; dy \\ &= 2\pi \int_{0}^{1} \left( y^{\frac{1}{3}} - y^{\frac{4}{3}} \right) \; dy \\ &= 2\pi \left[ \frac{3}{4}y^{\frac{4}{3}} - \frac{3}{7}y^{\frac{7}{3}} \right]_{0}^{1} \\ &= 2\pi \left( \frac{3}{4} - \frac{3}{7} \right)= \frac{9\pi}{14}\end{align*}$$
(e). $y = x^{2}, x = y^{2}$로 둘러쌓인 영역을 $y = -1$을 기준으로 회전
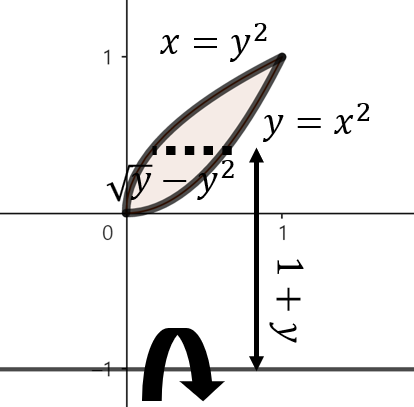
주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $y$에서 $y = -1$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $\sqrt{y} - y^{2}$이다. 이제, 구간 $0 \le y \le 1$에서 주어진 영역을 $y = -1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{0}^{1} 2\pi (1 + y) \left( y^{2} - \sqrt{y} \right) \; dy \\ &= 2\pi \int_{0}^{1} \left( y^{\frac{3}{2}} - y^{3} + y^{\frac{1}{2}} - y^{2} \right) \; dy \\ &= 2\pi \left[ \frac{2}{5}y^{\frac{5}{2}} - \frac{1}{4}y^{4} + \frac{2}{3}y^{\frac{3}{2}} - \frac{1}{3}y^{3} \right]_{0}^{1} \\ &= 2\pi \left( \frac{2}{5} - \frac{1}{4} + \frac{2}{3} - \frac{1}{3} \right)= \frac{29\pi}{30}\end{align*}$$
연습문제4. 주어진 적분이 어떤 회전체의 부피를 구하는 지 설명하라.
(a). $\int_{0}^{3} 2\pi x^{5} \; dx$
(b). $2\pi \int_{0}^{2} \frac{y}{1 + y^{2}} \; dy$
(c). $\int_{0}^{1} 2\pi (3 - y)(1 - y^{2}) \; dy$
(d). $\int_{0}^{\frac{\pi}{4}} 2\pi (\pi - x)(\cos(x) - \sin(x)) \; dx$
(a). $\int_{0}^{3} 2\pi x^{5} \; dx$
먼저 주어진 적분을 실린더 방법의 형태로 식을 바꾼다.
$$\begin{align*} \int_{0}^{3} 2\pi x^{5} \; dx&= \int_{0}^{3} 2\pi x \cdot x^{4} \; dx \end{align*}$$
따라서, $y = x^{4}, y = 0, x = 3$으로 둘러쌓인 영역을 $y$축을 중심으로 회전한 회전체의 부피를 의미한다.

(b). $2\pi \int_{0}^{2} \frac{y}{1 + y^{2}} \; dy$
먼저 주어진 적분을 실린더 방법의 형태로 식을 바꾼다.
$$\begin{align*} 2\pi \int_{0}^{2} \frac{y}{1 + y^{2}} \; dy&= \int_{0}^{2} 2\pi y \cdot \frac{1}{1 + y^{2}} \; dy \end{align*}$$
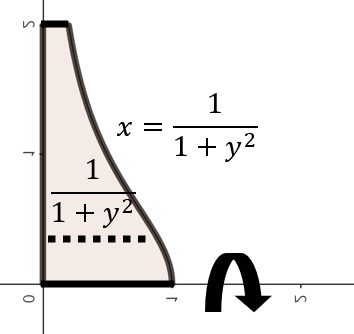
따라서, $x = \frac{1}{1 + y^{2}}, y = 0, y = 2$으로 둘러쌓인 영역을 $x$축을 중심으로 회전한 회전체의 부피를 의미한다.
(c). $\int_{0}^{1} 2\pi (3 - y)(1 - y^{2}) \; dy$
$x = y^{2}, x = 1, y = 0, y = 1$으로 둘러쌓인 영역을 $y = 3$축을 중심으로 회전한 회전체의 부피를 의미한다.

(d). $\int_{0}^{\frac{\pi}{4}} 2\pi (\pi - x)(\cos(x) - \sin(x)) \; dx$
$y = \cos(x), y = \sin(x), x = 0, x = \frac{\pi}{4}$으로 둘러쌓인 영역을 $x = \pi$축을 중심으로 회전한 회전체의 부피를 의미한다.

연습문제5. 주어진 함수들에 둘러쌓인 영역을 주어진 축을 기준으로 회전했을 때 얻을 수 있는 회전체의 부피를 구하여라.
(a). $y = -x^{2} + 6x - 8, y = 0$로 둘러쌓인 영역을 $y$축을 기준으로 회전
(b). $y = -x^{2} + 6x - 8, y = 0$로 둘러쌓인 영역을 $x$축을 기준으로 회전
(c). $y = 5, y = x + \frac{4}{x}$로 둘러쌓인 영역을 $x = -1$을 기준으로 회전
(a). $y = -x^{2} + 6x - 8, y = 0$로 둘러쌓인 영역을 $y$축을 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $y$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $-x^{2} + 6x - 8$이다. 이제, 구간 $2 \le x \le 4$에서 주어진 영역을 $y$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{2}^{4} 2\pi x \left( -x^{2} + 6x - 8 \right) \; dx \\ &= 2\pi \int_{2}^{4} \left( -x^{3} + 6x^{2} - 8x \right) \; dx \\ &= 2\pi \left[ -\frac{1}{4}x^{4} + 2x^{3} - 4x^{2} \right]_{2}^{4} \\ &= 2\pi \left[ \left( -\frac{1}{4} \cdot 4^{4} + 2 \cdot 4^{3} - 4 \cdot 4^{2} \right) - \left( -\frac{1}{4} \cdot 2^{4} + 2 \cdot 2^{3} - 4 \cdot 2^{2} \right) \right] = 8\pi \end{align*}$$
(b). $y = -x^{2} + 6x - 8, y = 0$로 둘러쌓인 영역을 $x$축을 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $x$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 반지름은 $-x^{2} + 6x - 8$이다. 이제, 구간 $2 \le x \le 4$에서 주어진 영역을 $x$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{2}^{4} \pi \left( -x^{2} + 6x - 8 \right)^{2} \; dx \\ &= \pi \int_{2}^{4} \left( x^{4} - 12x^{3} + 52x^{2} - 96x + 64 \right) \; dx \\ &= \pi \left[ \frac{1}{5}x^{4} - 3x^{4} + \frac{52}{3}x^{3} - 48x^{2} + 64x \right]_{2}^{4} \\ &= \pi \left[ \left( \frac{1}{5} \cdot 4^{4} - 3 \cdot 4^{4} + \frac{52}{3} \cdot 4^{3} - 48 \cdot 4^{2} + 64 \cdot 4 \right) - \left( \frac{1}{5} \cdot 2^{5} - 3 \cdot 2^{4} + \frac{52}{3} \cdot 2^{3} - 48 \cdot 2^{2} + 64 \cdot 2 \right) \right] = \frac{18}{5}\pi \end{align*}$$
(c). $y = 5, y = x + \frac{4}{x}$로 둘러쌓인 영역을 $x = -1$을 기준으로 회전

주어진 함수로 둘러쌓인 영역을 그림으로 그리면 위와 같이 그릴 수 있다. 여기서, 점 $x$에서 $x = -1$축을 기준으로 회전했을 때 얻을 수 있는 회전체 단면의 높이는 $5 - \left(x + \frac{4}{x}\right)$이다. 이제, 구간 $1 \le x \le 4$에서 주어진 영역을 $x = -1$축으로 회전시켰을 때 얻을 수 있는 회전체의 부피를 실린더 방법을 이용해 다음과 같이 구할 수 있다.
$$\begin{align*} V &= \int_{1}^{4} 2\pi (x + 1) \left( 5 - x - \frac{4}{x} \right) \; dx \\ &= 2\pi \int_{1}^{4} \left( -x^{2} + 5x + 1 - \frac{4}{x} \right) \; dx \\ &= 2\pi \left[ -\frac{1}{3}x^{3} + \frac{5}{2}x^{2} + x - 4\ln|x| \right]_{1}^{4} \\ &= 2\pi \left[ \left( -\frac{1}{3} \cdot 4^{3} + \frac{5}{2} \cdot 4^{2} + 4 - 4\ln(4) \right) - \left( -\frac{1}{3} \cdot 1^{3} + \frac{5}{2} \cdot 1^{2} + 1 - 4\ln(1) \right) \right] = 2\pi \left( 12 - 8\ln(2) \right) \end{align*}$$
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 부분적분 (1) | 2022.03.14 |
|---|---|
| 미적분학 - 함수의 평균 (0) | 2022.03.12 |
| 미적분학 - 입체 부피 구하기 (0) | 2022.03.05 |
| 미적분학 - 두 곡선 사이의 넓이 (0) | 2022.03.04 |
| 미적분학 - 치환적분 (0) | 2022.03.03 |
