안녕하세요. 미적분학 관련 포스팅은 모두 끝났지만 앞으로 몇 가지 보충할 주제가 있으면 쓰기로 했기 때문에 오늘은 쌍곡선 함수 (Hyperbolic Function)에 대해서 알아보도록 하겠습니다.
정의1. 쌍곡선 함수 (Hyperbolic Functions)
1). $\sinh(x) = \frac{e^{x} - e^{-x}}{2}$
2). $\cosh(x) = \frac{e^{x} + e^{-x}}{2}$
3). $\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$
4). $\text{csch}(x) = \frac{1}{\sinh(x)} = \frac{2}{e^{x} - e^{-x}}$
5). $\text{sech}(x) = \frac{1}{\cosh(x)} = \frac{2}{e^{x} + e^{-x}}$
6). $\coth(x) = \frac{1}{\tanh(x)} = \frac{\cosh(x)}{\sinh(x)} = \frac{e^{x} + e^{-x}}{e^{x} - e^{-x}}$
설명
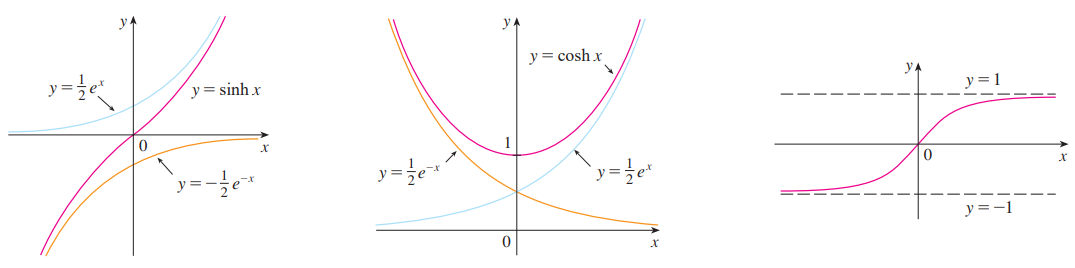
정의1을 보시면 기존에 저희가 배웠던 삼각함수와 유사한 기호를 사용한다는 것을 볼 수 있습니다. 삼각함수와 가장 관련이 깊은 도형은 원이죠. 그와 반면에 쌍곡선 함수와 가장 관련이 깉은 함수는 쌍곡선 (hyperbola) 입니다. 기본적인 쌍곡선 함수들의 정의역과 치역을 그림으로 보면 $\sinh$ 함수는 모두 $\mathbb{R}$이고 $\cosh$ 함수는 정의역은 $\mathbb{R}$이고 치역은 $[1, \infty)$입니다. 마지막으로 $\tanh$ 함수의 정의역과 치역은 각각 $\mathbb{R}$과 $[-1, 1]$입니다. 잘 보시면 $\tanh$에서 수평점근선이 $y = \pm 1$임을 알 수 있죠. 실제로 다양한 곳에서 쌍곡선 함수가 활용되고 있습니다. 대표적으로 바다의 파도의 속도를 수학적으로 모델링하게 되면 쌍곡선 함수가 들어가게 되죠.
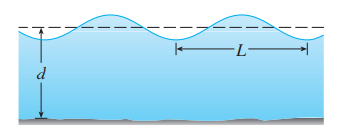
$$v = \sqrt{\frac{gL}{2\pi}}\tanh \left( \frac{2\pi d}{L} \right)$$
이때, $g$는 중력 가속도입니다.
정리1. 쌍곡선 함수의 성질
1). $\sinh(-x) = -\sinh(x)$
2). $\cosh(-x) = \cosh(x)$
3). $\sinh(x + y) = \sinh(x)\cosh(y) + \cosh(x)\sinh(y)$
4). $\cosh(x + y) = \cosh(x)\cosh(y) + \sinh(x)\sinh(y)$
5). $\cosh^{2}(x) - \sinh^{2}(x) = 1$
설명
쌍곡선 함수의 성질에 대한 증명은 모두 정의를 적절하게 활용하면 쉽게 증명할 수 있습니다. 예를 들어, 성질 1)와 2)를 증명해보도록 하죠.
$$\sinh(-x) = \frac{e^{-x} - e^{-(-x)}}{2} = - \frac{e^{x} - e^{-x}}{2} = -\sinh(x)$$
$$\cosh(-x) = \frac{e^{-x} + e^{-(-x)}}{2} = \frac{e^{x} + e^{-x}}{2} = \cosh(x)$$
이와 같은 방법으로 성질 3)와 4)도 증명해보도록 하겠습니다.
$$\begin{align*} \sinh(x)\cosh(y) + \sinh(y)\cosh(x)&= \frac{e^{x} - e^{-x}}{2} \cdot \frac{e^{y} + e^{-y}}{2} + \frac{e^{y} - e^{-y}}{2} \cdot \frac{e^{x} + e^{-x}}{2} \\ &= \frac{e^{x + y} + e^{x - y} - e^{-(x - y)} - e^{-(x + y)}}{4} + \frac{e^{x + y} + e^{-(x - y)} - e^{x - y} - e^{-(x + y)}}{4} \\ &= \frac{e^{x + y} - e^{-(x + y)}}{2} = \sinh(x + y)\end{align*}$$
$$\begin{align*} \cosh(x)\cosh(y) + \sinh(y)\sinh(x)&= \frac{e^{x} + e^{-x}}{2} \cdot \frac{e^{y} + e^{-y}}{2} + \frac{e^{y} - e^{-y}}{2} \cdot \frac{e^{x} - e^{-x}}{2} \\ &= \frac{e^{x + y} + e^{x - y} + e^{-(x - y)} + e^{-(x + y)}}{4} + \frac{e^{x + y} - e^{-(x - y)} - e^{x - y} + e^{-(x + y)}}{4} \\ &= \frac{e^{x + y} + e^{-(x + y)}}{2} = \cosh(x + y)\end{align*}$$
마지막으로 성질 5)까지 증명해보도록 하죠.
$$\begin{align*} \cosh^{2}(x) - \sinh^{2}(x) &= \left(\frac{e^{x} + e^{-x}}{2}\right)^{2} - \left( \frac{e^{x} - e^{-x}}{2} \right)^{2} \\ &= \frac{e^{2x} + 2 + e^{-2x}}{4} - \frac{e^{2x} - 2 + e^{-2x}}{4} = \frac{4}{4} = 1 \end{align*}$$
이와 같이 정의를 이용하면 아주 쉽게 증명할 수 있습니다.
정리2. 쌍곡선 함수의 미분
1). $\frac{d}{dx} [\sinh(x)] = \cosh(x)$
2). $\frac{d}{dx} [\cosh(x)] = \sinh(x)$
3). $\frac{d}{dx} [\tanh(x)] = \text{sech}^{2}(x)$
4). $\frac{d}{dx} [\text{csch}(x)] = -\text{csch}(x)\coth(x)$
5). $\frac{d}{dx} [\text{sech}(x)] = -\text{sech}(x)\tanh(x)$
6). $\frac{d}{dx} [\coth(x)] = -\text{csch}^{2}(x)$
설명
미분법도 마찬가지로 정의를 이용하면 쉽게 증명할 수 있습니다. 먼저 간단한 $\sinh$와 $\cosh$의 미분부터 보도록 하죠.
$$\frac{d}{dx} [\sinh(x)] = \frac{d}{dx} \left[ \frac{e^{x} - e^{-x}}{2} \right] = \frac{e^{x} + e^{-x}}{2} = \cosh(x)$$
$$\frac{d}{dx} [\cosh(x)] = \frac{d}{dx} \left[ \frac{e^{x} + e^{-x}}{2} \right] = \frac{e^{x} - e^{-x}}{2} = \sinh(x)$$
다음으로 $\tanh$의 미분입니다.
$$\frac{d}{dx} [\tanh(x)] = \frac{d}{dx} \left[ \frac{\sinh(x)}{\cosh(x)} \right] = \frac{\cosh(x) \cosh(x) - \sinh(x) \sinh(x)}{\cosh^{2}(x)} = \frac{1}{\cosh^{2}(x)} = \text{sech}^{2}(x)$$
마지막으로 $\text{csch}, \text{sech}, \text{coth}$ 함수들의 미분을 증명해보겠습니다.
$$\frac{d}{dx} [\text{csch}(x)] = \frac{d}{dx} \left[ \frac{1}{\sinh(x)} \right] = -\frac{\cosh(x)}{\sinh^{2}(x)} = -\text{csch}(x)\text{coth}(x)$$
$$\frac{d}{dx} [\text{sech}(x)] = \frac{d}{dx} \left[ \frac{1}{\cosh(x)} \right] = -\frac{\sinh(x)}{\cosh^{2}(x)} = -\text{sech}(x)\tanh(x)$$
$$\frac{d}{dx} [\coth(x)] = \frac{d}{dx} \left[ \frac{1}{\tanh(x)} \right] = -\frac{\text{sech}^{2}(x)}{\tanh^{2}(x)} = -\frac{1}{\cosh^{2}(x)} \cdot \frac{\cosh^{2}(x)}{\sinh^{2}(x)} = -\text{csch}^{2}(x)$$
정의2. 역쌍곡선 함수 (inverse hyperbolic functions)
1). $y = \sinh^{-1}(x) \leftrightarrow x = \sinh(y) = \frac{e^{y} - e^{-y}}{2} \rightarrow \sinh^{-1}(x) = \ln\left(x + \sqrt{x^{2} + 1}\right)$
2). $y = \cosh^{-1}(x) \leftrightarrow x = \cosh(y) = \frac{e^{y} + e^{-y}}{2} \rightarrow \cosh^{-1}(x) = \ln\left(x + \sqrt{x^{2} - 1}\right)$
3). $y = \tanh^{-1}(x) \leftrightarrow x = \tanh(y) = \frac{e^{y} - e^{-y}}{e^{y} + e^{-y}} \rightarrow \tanh^{-1}(x) = \frac{1}{2}\ln\left(\frac{1 + x}{1 - x}\right)$
정리3. 역쌍곡선 함수의 미분
1). $\frac{d}{dx} [\sinh^{-1}(x)] = \frac{1}{\sqrt{x^{2} + 1}}$
2). $\frac{d}{dx} [\cosh^{-1}(x)] = \frac{1}{\sqrt{x^{2} - 1}}$
3). $\frac{d}{dx} [\tanh^{-1}(x)] = \frac{1}{1 - x^{2}}$
설명
역쌍곡선 함수의 미분은 음함수 함수의 미분과 쌍곡선 함수의 정의를 적절히 활용하면 쉽게 증명할 수 있습니다.
$$\sinh^{-1}(x) = y \rightarrow \sinh(y) = x \rightarrow \cosh(y)\frac{dy}{dx} = 1 \rightarrow \frac{dy}{dx} = \frac{1}{\cosh(y)} = \frac{1}{\sqrt{1 + \sinh^{2}(x)}} = \frac{1}{\sqrt{1 + x^{2}}}$$
$$\cosh^{-1}(x) = y \rightarrow \cosh(y) = x \rightarrow \sinh(y)\frac{dy}{dx} = 1 \rightarrow \frac{dy}{dx} = \frac{1}{\sinh(y)} = \frac{1}{\sqrt{\cosh^{2}(x) - 1}} = \frac{1}{\sqrt{x^{2} - 1}}$$
$$\tanh^{-1}(x) = y \rightarrow \tanh(y) = x \rightarrow \text{sech}^{2}(y)\frac{dy}{dx} = 1 \rightarrow \frac{dy}{dx} = \frac{1}{\text{sech}^{2}(y)} = \frac{1}{1 - \tanh^{2}x} = \frac{1}{1 - x^{2}}$$
연습문제1. 각 쌍곡선 함수의 값을 구하여라.
(a). $\sinh (0)$
(b). $\tanh (0)$
(c). $\sinh(ln (2))$
(d). $\cosh (3)$
(e). $\text{sech} (0)$
(f). $\sinh (1)$
(a). $\sinh (0) = \frac{e^{0} - e^{0}}{2} = 0$
(b). $\tanh (0) = \frac{e^{0} - e^{0}}{\e^{0} + e^{0}} = 0$
(c). $\sinh(ln (2)) = \frac{e^{\ln (2)} - e^{-\ln (2)}}{2} = \frac{2 - \frac{1}{2}}{2} = \frac{3}{4}$
(d). $\cosh (3) = \frac{e^{3} + e^{-3}}{2}$
(e). $\text{sech} (0) = \frac{2}{e^{0} + e^{0}} = 1$
(f). $\sinh (1) = \frac{e^{1} - e^{-1}}{2}$
연습문제2. 각 쌍곡선 함수의 값을 구하여라.
(a). $\cosh (0)$
(b). $\tanh (1)$
(c). $\sinh (2)$
(d). $\cosh(\ln (3))$
(e). $\cosh^{-1} (1)$
(f). $\sinh^{-1} (1)$
(a). $\cosh (0) = \frac{e^{0} + e^{0}}{2} = 1$
(b). $\tanh (1) = \frac{e^{1} - e^{-1}}{e^{1} + e^{-1}}$
(c). $\sinh (2) = \frac{e^{2} - e^{-2}}{2}$
(d). $\cosh(\ln (3)) = \frac{e^{\ln (3)} - e^{-\ln (3)}}{2} = \frac{3 - \frac{1}{3}}{2} = \frac{4}{3}$
(e). $\cosh^{-1} (1) = 0$
(f). $\sinh^{-1} (1)$
$\sinh^{-1} (1) = a$라고 하자. 역함수와 쌍곡선 함수의 정의에 의해 $\sinh (a) = \frac{e^{a} - e^{-a}}{2} = 1$이므로 식을 아래와 같이 정리할 수 있다.
$$e^{2a} - 2e^{a} - 1 = 0 \rightarrow e^{a} = \frac{2 \pm \sqrt{5}}{2}$$
이때, $e^{a} > 0$이므로 $e^{a} = \frac{2 + \sqrt{5}}{2}$이다. 양변에 자연상수 $e$를 밑으로 하는 자연로그를 취하면 $a = \ln \left( \frac{2 + \sqrt{5}}{2} \right)$임을 알 수 있다.
연습문제3. 주어진 쌍곡선 함수들의 성질을 증명하시오.
(a). $\sinh(-x) = -\sinh(x)$
(b). $\cosh(-x) = \cosh(x)$
(c). $\cosh(x) + \sinh(x) = e^{x}$
(d). $\cosh(x) - \sinh(x) = e^{-x}$
(a). $\sinh(-x) = -\sinh(x)$
$$\begin{align*} \sinh (-x) &= \frac{e^{-x} - e^{-(-x)}}{2} \\ &= -\frac{e^{x} - e^{-x}}{2} = -\sinh(x) \end{align*}$$
(b). $\cosh(-x) = \cosh(x)$
$$\begin{align*} \cosh (-x) &= \frac{e^{-x} + e^{-(-x)}}{2} \\ &= \frac{e^{x} + e^{-x}}{2} = \cosh(x) \end{align*}$$
(c). $\cosh(x) + \sinh(x) = e^{x}$
$$\begin{align*} \cosh (x) + \sinh (x) &= \frac{e^{x} + e^{-x}}{2} + \frac{e^{x} - e^{-x}}{2} = e^{x} \end{align*}$$
(d). $\cosh(x) - \sinh(x) = e^{-x}$
$$\begin{align*} \cosh (x) - \sinh (x) &= \frac{e^{x} + e^{-x}}{2} - \frac{e^{x} - e^{-x}}{2} = e^{-x} \end{align*}$$
연습문제4. 주어진 쌍곡선 함수들의 성질을 증명하시오.
(a). $\coth^{2}(x) - 1 = \text{csch}^{2}(x)$
(b). $\tanh(x + y) = \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)}$
(c). $\sinh(2x) = 2\sinh(x)\cosh(x)$
(d). $\cosh(2x) = \cosh^{2}(x) + \sinh^{2}(x)$
(e). $\tanh(\ln(x)) = \frac{x^{2} - 1}{x^{2} + 1}$
(f). $\frac{1 + \tanh(x)}{1 - \tanh(x)} = e^{2x}$
(g). $(\cosh(x) + \sinh(x))^{n} = \cosh(nx) + \sinh(nx)$
(a). $\coth^{2}(x) - 1 = \text{csch}^{2}(x)$
$$\begin{align*} &\cosh^{2}(x) - \sinh^{2}(x) = 1 \\ \Rightarrow& \frac{\cosh^{2}(x)}{\sinh^{2}(x)} - 1 = \frac{1}{\sinh^{2}(x)} \\ \Rightarrow& \coth^{2}(x) - 1 = \text{csch}^{2}(x) \end{align*}$$
(b). $\tanh(x + y) = \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)}$
$$\begin{align*} \tanh(x + y) &= \frac{\sinh(x + y)}{\cosh(x + y)} \\ &= \frac{\sinh(x)\cosh(y) + \sinh(y)\cosh(x)}{\cosh(x)\cosh(y) + \sinh(x)\sinh(y)} \\ &= \frac{\frac{\sinh(x)}{\cosh(x)} + \frac{\sinh(y)}{\cosh(y)}}{1 + \left( \frac{\sinh(x)}{\cosh(x)} \right) \left( \frac{\sinh(y)}{\cosh(y)} \right)} \\ &= \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)} \end{align*}$$
(c). $\sinh(2x) = 2\sinh(x)\cosh(x)$
$$\begin{align*} \sinh(2x) &= \sinh(x + x) \\ &= \sinh(x)\cosh(x) + \sinh(x)cosh(x) \\ &= 2\sinh(x)\cosh(x) \end{align*}$$
(d). $\cosh(2x) = \cosh^{2}(x) + \sinh^{2}(x)$
$$\begin{align*} \cosh(2x) &= \cosh(x + x) \\ &= \cosh(x)\cosh(x) + \sinh(x)\sinh(x) \\ &= \cosh^{2}(x) + \sinh^{2}(x) \end{align*}$$
(e). $\tanh(\ln(x)) = \frac{x^{2} - 1}{x^{2} + 1}$
$$\begin{align*} \tanh(\ln(x)) &= \frac{e^{\ln(x)} - e^{-\ln(x)}}{e^{\ln(x)} + e^{-\ln(x)}} \\ &= \frac{x - \frac{1}{x}}{x + \frac{1}{x}} \\ &= \frac{x^{2} - 1}{x^{2} + 1} \end{align*}$$
(f). $\frac{1 + \tanh(x)}{1 - \tanh(x)} = e^{2x}$
$$\begin{align*} \frac{1 + \tanh(x)}{1 - \tanh(x)} &= \frac{1 + \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}}{1 - \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}} \\ &= \frac{(e^{x} + e^{-x}) + (e^{x} - e^{-x})}{(e^{x} + e^{-x}) - (e^{x} - e^{-x})} \\ &= \frac{2e^{x}}{e^{-x}} = e^{2x} \end{align*}$$
(g). $(\cosh(x) + \sinh(x))^{n} = \cosh(nx) + \sinh(nx)$
$$\begin{align*} (\cosh(x) + \sinh(x))^{n} &= \left( \frac{e^{x} + e^{-x}}{2} + \frac{e^{x} - e^{-x}}{2} \right)^{n} \\ &= [e^{x}]^{n} = e^{nx} \\ &= \frac{e^{nx} + e^{-nx}}{2} + \frac{e^{nx} - e^{-nx}}{2} \\ &= \cosh(nx) + \sinh(nx) \end{align*}$$
연습문제5. 각 쌍곡선 함수의 극한을 구하여라.
(a). $\lim_{x \rightarrow \infty} \tanh(x)$
(b). $\lim_{x \rightarrow \infty} \sinh(x)$
(c). $\lim_{x \rightarrow \infty} \text{sech}(x)$
(d). $\lim_{x \rightarrow 0^{+}} \coth(x)$
(a). $\lim_{x \rightarrow \infty} \tanh(x) = \lim_{x \rightarrow \infty} \left( \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} \right) = \lim_{x \rightarrow \infty} \left( \frac{1 - e^{-2x}}{1 + e^{-2x}} \right) = 1$
(b). $\lim_{x \rightarrow \infty} \sinh(x) = \lim_{x \rightarrow \infty} \frac{e^{x} - e^{-x}}{2} = \infty$
(c). $\lim_{x \rightarrow \infty} \text{sech}(x) = \lim_{x \rightarrow \infty} \frac{2}{e^{x} + e^{-x}} = 0$
(d). $\lim_{x \rightarrow 0^{+}} \coth(x) = \lim_{x \rightarrow 0^{+}} \frac{e^{x} + e^{-x}}{e^{x} - e^{-x}} = \infty$
연습문제6. 주어진 함수들의 도함수를 구하여라.
(a). $f(x) = \tanh(1 + e^{2x})$
(b). $g(x) = \cosh(\ln(x))$
(c). $y = x\coth(1 + x^{2})$
(d). $f(t) = \text{csch} (t) (1 - \ln (\text{csch}(t)))$
(e). $y = \sinh(\cosh(x))$
(f). $y = \sqrt[4]{\frac{1 + \tanh(x)}{1 - \tanh(x)}}$
(g). $y = x^{2}\sinh^{-1}(2x)$
(a). $f(x) = \tanh(1 + e^{2x})$
$$f^{'}(x) = 2e^{2x}\text{sech}^{2}(1 + e^{2x})$$
(b). $g(x) = \cosh(\ln(x))$
$$g^{'}(x) = \frac{\sinh(\ln(x))}{x}$$
(c). $y = x\coth(1 + x^{2})$
$$y^{'} = \coth(1 + x^{2}) - 2x^{2}\text{csch}^{2}(1 + x^{2})$$
(d). $f(t) = \text{csch} (t) (1 - \ln (\text{csch}(t)))$
$$\begin{align*} y^{'} &= -\text{csch}(t)\coth(t) (1 - \ln(\text{csch}(t))) + \text{csch}(x) \cdot \frac{\text{csch}(t)\coth(t)}{\text{csch}(t)} \\ &= -\text{csch}(t)\coth(t) + \text{csch}(t)\coth(t)\ln (\text{csch}(t)) + \text{csch}(t) \coth(t) \\ &= \text{csch}(t)\coth(t)\ln(\text{csch}(t))\end{align*}$$
(e). $y = \sinh(\cosh(x))$
$$\begin{align*} y^{'} &= -\sinh(x)\cosh(\cosh(x))\end{align*}$$
(f). $y = \sqrt[4]{\frac{1 + \tanh(x)}{1 - \tanh(x)}} = \sqrt[4]{e^{2x}} = e^{\frac{x}{2}}$
$$\begin{align*} y^{'} &= \frac{1}{2}e^{\frac{x}{2}} \end{align*}$$
(g). $y = x^{2}\sinh^{-1}(2x)$
$$\begin{align*} y^{'} &= 2x\sinh^{-1}(2x) + x^{2} \cdot \left( \frac{2}{\sqrt{1 + 4x^{2}}} \right) \\ &= 2x\sinh^{-1}(2x) + \frac{2x^{2}}{\sqrt{1 + 4x^{2}}}\end{align*}$$
연습문제7. 주어진 함수들의 도함수를 구하여라.
(a). $f(x) = x\sinh(x) - \cosh(x)$
(b). $h(x) = \ln (\cosh(x))$
(c). $y = e^{\cosh(3x)}$
(d). $f(t) = \text{sech}^{2}(e^{t})$
(e). $y = \arctan(\tanh(x))$
(f). $G(x) = \frac{1 - \cosh(x)}{1 + \cosh(x)}$
(g). $y = \tanh^{-1} (\sqrt{x})$
(a). $f(x) = x\sinh(x) - \cosh(x)$
$$\begin{align*} f^{'}(x) &= \sinh(x) + x\cosh(x) - \sinh(x) \\ &= x\cosh(x) \end{align*}$$
(b). $h(x) = \ln (\cosh(x))$
$$\begin{align*} h^{'}(x) &= \frac{\sinh(x)}{\cosh(x)} \\ &= \tanh(x) \end{align*}$$
(c). $y = e^{\cosh(3x)}$
$$\begin{align*} y^{'} &= 3\sinh(3x)e^{\cosh(3x)} \end{align*}$$
(d). $f(t) = \text{sech}^{2}(e^{t})$
$$\begin{align*} f^{'}(t) &= 2e^{t} \cdot (-\text{sech}(e^{t})\tanh(e^{t})) \text{sech}(e^{t}) \\ &= -2e^{t}\text{sech}^{2}(e^{t})\tanh(e^{t}) \end{align*}$$
(e). $y = \arctan(\tanh(x))$
$$\begin{align*} y^{'} &= \frac{\text{sech}^{2}(x)}{1 + \tanh^{2}(x)} \end{align*}$$
(f). $G(x) = \frac{1 - \cosh(x)}{1 + \cosh(x)}$
$$\begin{align*} G^{'}(x) &= \frac{-\sinh(x) (1 + \cosh(x)) - \sinh(x)(1 - \cosh(x))}{(1 + \cosh(x))^{2}} \\ &= -\frac{2\sinh(x)}{(1 + \cosh(x))^{2}}\end{align*}$$
(g). $y = \tanh^{-1} (\sqrt{x})$
$$\begin{align*} y^{'} &= \frac{1}{1 + (\sqrt{x})^{2}} \cdot \frac{1}{2\sqrt{x}} \\ &= \frac{1}{2\sqrt{x}(1 + x)}\end{align*}$$
연습문제8. 주어진 함수들의 도함수를 구하여라.
(a). $y = x\tanh^{-1}(x) + \ln (\sqrt{1 - x^{2}})$
(b). $y = x\sinh^{-1} \left( \frac{x}{3} \right) - \sqrt{9 + x^{2}}$
(c). $y = \text{sech}^{-1} (\sqrt{1 - x^{2}}), x > 0$
(d). $y = \coth^{-1}(\sqrt{x^{2} + 1})$
(a). $y = x\tanh^{-1}(x) + \ln (\sqrt{1 - x^{2}})$
$$\begin{align*} y^{'} &= \tanh^{-1}(x) + \frac{x}{1 + x^{2}} + \frac{1}{1 - x^{2}} \cdot \left( \frac{-2x}{2\sqrt{1 - x^{2}}} \right) \\ &= \tanh^{-1}(x) + \frac{x}{1 + x^{2}} - \frac{x}{\sqrt{1 - x^{2}}}\end{align*}$$
(b). $y = x\sinh^{-1} \left( \frac{x}{3} \right) - \sqrt{9 + x^{2}}$
$$\begin{align*} y^{'} &=\sinh^{-1} \left( \frac{x}{3} \right) + x \cdot \frac{\frac{1}{3}}{\sqrt{1 - \left( \frac{x}{3} \right)^{2}}} - \frac{2x}{2\sqrt{9 + x^{2}}} \\ &= \sinh^{-1} \left( \frac{x}{3} \right) + \frac{x}{\sqrt{9 - x^{2}}} - \frac{x}{\sqrt{9 + x^{2}}}\end{align*}$$
(c). $y = \text{sech}^{-1} (\sqrt{1 - x^{2}}), x > 0$
$$\begin{align*} y^{'} &= \frac{-2x}{2\sqrt{1 - x^{2}}} \cdot \frac{1}{\sqrt{1 - (\sqrt{1 - x^{2}})^{2}}} \\ &= -\frac{x}{\sqrt{1 - x^{2}}} \cdot \frac{1}{x} \\ &= -\frac{1}{\sqrt{1 - x^{2}}} \end{align*}$$
(d). $y = \coth^{-1}(\sqrt{x^{2} + 1})$
$$\begin{align*} y^{'} &= \frac{2x}{2\sqrt{1 + x^{2}}} \cdot \frac{1}{1 - (\sqrt{1 + x^{2}})^{2}} \\ &= \frac{x}{\sqrt{1 + x^{2}}} \cdot \left( -\frac{1}{x^{2}} \right) \\ &= -\frac{1}{x\sqrt{x^{2} + 1}}\end{align*}$$
연습문제9. $\lim_{x \rightarrow \infty} \frac{\sinh(x)}{e^{x}}$를 구하여라.
$$\begin{align*} \lim_{x \rightarrow \infty} \frac{\sinh(x)}{e^{x}} &= \lim_{x \rightarrow \infty} \frac{e^{x} - e^{-x}}{2e^{x}} \\ &= \lim_{x \rightarrow \infty} \frac{1}{2} (1 - e^{-2x}) = \frac{1}{2} \end{align*}$$
연습문제10. $x = \ln(\sec(\theta) + \tan(\theta))$일 때, $\sec(\theta) = \cosh(x)$임을 보여라.
$x = \ln (\sec(\theta) + \tan(\theta))$이므로 $e^{x} = \sec(\theta) + \tan(\theta) = \frac{1 + \sin(\theta)}{\cos(\theta)}$이다. 이와 동일한 방법으로 양변에 음수를 취하고 자연상수를 취해주면 $e^{-x} = \frac{\cos(\theta)}{1 + \sin(\theta)}$를 얻을 수 있다.
$$\begin{align*} e^{x} + e^{-x} &= \frac{1 + \sin(\theta)}{\cos(\theta)} + \frac{\cos(\theta)}{1 + \sin(\theta)} \\ &= \frac{(1 + \sin(\theta))^{2} + \cos^{2}(\theta)}{\cos(\theta)(1 + \sin(\theta))} \\ &= \frac{1 + 2\sin(\theta) + (\sin^{2}(\theta) + \cos^{2}(\theta))}{\cos(\theta)(1 + \sin(\theta))} \\ &= \frac{2(1 + \sin(\theta))}{\cos(\theta) (1 + \sin(\theta))} \\ &= \frac{2}{\cos(\theta)} = 2\sec(\theta) \end{align*}$$
따라서, $\sec(\theta) = \frac{e^{x} + e^{-x}}{2} = \cosh(x)$이다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.09.21 : 연습문제1-5 추가
22.09.22 : 연습문제6-10 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 적분 연습문제 (0) | 2022.11.30 |
|---|---|
| 미적분학 - 미분 규칙 연습문제 (0) | 2022.09.22 |
| 미적분학 - 목차 (0) | 2022.08.03 |
| 미적분학 - 발산 정리 (0) | 2022.08.02 |
| 미적분학 - 스토크스의 정리 (0) | 2022.08.01 |
안녕하세요. 미적분학 관련 포스팅은 모두 끝났지만 앞으로 몇 가지 보충할 주제가 있으면 쓰기로 했기 때문에 오늘은 쌍곡선 함수 (Hyperbolic Function)에 대해서 알아보도록 하겠습니다.
정의1. 쌍곡선 함수 (Hyperbolic Functions)

1). $\sinh(x) = \frac{e^{x} - e^{-x}}{2}$
2). $\cosh(x) = \frac{e^{x} + e^{-x}}{2}$
3). $\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$
4). $\text{csch}(x) = \frac{1}{\sinh(x)} = \frac{2}{e^{x} - e^{-x}}$
5). $\text{sech}(x) = \frac{1}{\cosh(x)} = \frac{2}{e^{x} + e^{-x}}$
6). $\coth(x) = \frac{1}{\tanh(x)} = \frac{\cosh(x)}{\sinh(x)} = \frac{e^{x} + e^{-x}}{e^{x} - e^{-x}}$
설명
정의1을 보시면 기존에 저희가 배웠던 삼각함수와 유사한 기호를 사용한다는 것을 볼 수 있습니다. 삼각함수와 가장 관련이 깊은 도형은 원이죠. 그와 반면에 쌍곡선 함수와 가장 관련이 깉은 함수는 쌍곡선 (hyperbola) 입니다. 기본적인 쌍곡선 함수들의 정의역과 치역을 그림으로 보면 $\sinh$ 함수는 모두 $\mathbb{R}$이고 $\cosh$ 함수는 정의역은 $\mathbb{R}$이고 치역은 $[1, \infty)$입니다. 마지막으로 $\tanh$ 함수의 정의역과 치역은 각각 $\mathbb{R}$과 $[-1, 1]$입니다. 잘 보시면 $\tanh$에서 수평점근선이 $y = \pm 1$임을 알 수 있죠. 실제로 다양한 곳에서 쌍곡선 함수가 활용되고 있습니다. 대표적으로 바다의 파도의 속도를 수학적으로 모델링하게 되면 쌍곡선 함수가 들어가게 되죠.

$$v = \sqrt{\frac{gL}{2\pi}}\tanh \left( \frac{2\pi d}{L} \right)$$
이때, $g$는 중력 가속도입니다.
정리1. 쌍곡선 함수의 성질
1). $\sinh(-x) = -\sinh(x)$
2). $\cosh(-x) = \cosh(x)$
3). $\sinh(x + y) = \sinh(x)\cosh(y) + \cosh(x)\sinh(y)$
4). $\cosh(x + y) = \cosh(x)\cosh(y) + \sinh(x)\sinh(y)$
5). $\cosh^{2}(x) - \sinh^{2}(x) = 1$
설명
쌍곡선 함수의 성질에 대한 증명은 모두 정의를 적절하게 활용하면 쉽게 증명할 수 있습니다. 예를 들어, 성질 1)와 2)를 증명해보도록 하죠.
$$\sinh(-x) = \frac{e^{-x} - e^{-(-x)}}{2} = - \frac{e^{x} - e^{-x}}{2} = -\sinh(x)$$
$$\cosh(-x) = \frac{e^{-x} + e^{-(-x)}}{2} = \frac{e^{x} + e^{-x}}{2} = \cosh(x)$$
이와 같은 방법으로 성질 3)와 4)도 증명해보도록 하겠습니다.
$$\begin{align*} \sinh(x)\cosh(y) + \sinh(y)\cosh(x)&= \frac{e^{x} - e^{-x}}{2} \cdot \frac{e^{y} + e^{-y}}{2} + \frac{e^{y} - e^{-y}}{2} \cdot \frac{e^{x} + e^{-x}}{2} \\ &= \frac{e^{x + y} + e^{x - y} - e^{-(x - y)} - e^{-(x + y)}}{4} + \frac{e^{x + y} + e^{-(x - y)} - e^{x - y} - e^{-(x + y)}}{4} \\ &= \frac{e^{x + y} - e^{-(x + y)}}{2} = \sinh(x + y)\end{align*}$$
$$\begin{align*} \cosh(x)\cosh(y) + \sinh(y)\sinh(x)&= \frac{e^{x} + e^{-x}}{2} \cdot \frac{e^{y} + e^{-y}}{2} + \frac{e^{y} - e^{-y}}{2} \cdot \frac{e^{x} - e^{-x}}{2} \\ &= \frac{e^{x + y} + e^{x - y} + e^{-(x - y)} + e^{-(x + y)}}{4} + \frac{e^{x + y} - e^{-(x - y)} - e^{x - y} + e^{-(x + y)}}{4} \\ &= \frac{e^{x + y} + e^{-(x + y)}}{2} = \cosh(x + y)\end{align*}$$
마지막으로 성질 5)까지 증명해보도록 하죠.
$$\begin{align*} \cosh^{2}(x) - \sinh^{2}(x) &= \left(\frac{e^{x} + e^{-x}}{2}\right)^{2} - \left( \frac{e^{x} - e^{-x}}{2} \right)^{2} \\ &= \frac{e^{2x} + 2 + e^{-2x}}{4} - \frac{e^{2x} - 2 + e^{-2x}}{4} = \frac{4}{4} = 1 \end{align*}$$
이와 같이 정의를 이용하면 아주 쉽게 증명할 수 있습니다.
정리2. 쌍곡선 함수의 미분
1). $\frac{d}{dx} [\sinh(x)] = \cosh(x)$
2). $\frac{d}{dx} [\cosh(x)] = \sinh(x)$
3). $\frac{d}{dx} [\tanh(x)] = \text{sech}^{2}(x)$
4). $\frac{d}{dx} [\text{csch}(x)] = -\text{csch}(x)\coth(x)$
5). $\frac{d}{dx} [\text{sech}(x)] = -\text{sech}(x)\tanh(x)$
6). $\frac{d}{dx} [\coth(x)] = -\text{csch}^{2}(x)$
설명
미분법도 마찬가지로 정의를 이용하면 쉽게 증명할 수 있습니다. 먼저 간단한 $\sinh$와 $\cosh$의 미분부터 보도록 하죠.
$$\frac{d}{dx} [\sinh(x)] = \frac{d}{dx} \left[ \frac{e^{x} - e^{-x}}{2} \right] = \frac{e^{x} + e^{-x}}{2} = \cosh(x)$$
$$\frac{d}{dx} [\cosh(x)] = \frac{d}{dx} \left[ \frac{e^{x} + e^{-x}}{2} \right] = \frac{e^{x} - e^{-x}}{2} = \sinh(x)$$
다음으로 $\tanh$의 미분입니다.
$$\frac{d}{dx} [\tanh(x)] = \frac{d}{dx} \left[ \frac{\sinh(x)}{\cosh(x)} \right] = \frac{\cosh(x) \cosh(x) - \sinh(x) \sinh(x)}{\cosh^{2}(x)} = \frac{1}{\cosh^{2}(x)} = \text{sech}^{2}(x)$$
마지막으로 $\text{csch}, \text{sech}, \text{coth}$ 함수들의 미분을 증명해보겠습니다.
$$\frac{d}{dx} [\text{csch}(x)] = \frac{d}{dx} \left[ \frac{1}{\sinh(x)} \right] = -\frac{\cosh(x)}{\sinh^{2}(x)} = -\text{csch}(x)\text{coth}(x)$$
$$\frac{d}{dx} [\text{sech}(x)] = \frac{d}{dx} \left[ \frac{1}{\cosh(x)} \right] = -\frac{\sinh(x)}{\cosh^{2}(x)} = -\text{sech}(x)\tanh(x)$$
$$\frac{d}{dx} [\coth(x)] = \frac{d}{dx} \left[ \frac{1}{\tanh(x)} \right] = -\frac{\text{sech}^{2}(x)}{\tanh^{2}(x)} = -\frac{1}{\cosh^{2}(x)} \cdot \frac{\cosh^{2}(x)}{\sinh^{2}(x)} = -\text{csch}^{2}(x)$$
정의2. 역쌍곡선 함수 (inverse hyperbolic functions)
1). $y = \sinh^{-1}(x) \leftrightarrow x = \sinh(y) = \frac{e^{y} - e^{-y}}{2} \rightarrow \sinh^{-1}(x) = \ln\left(x + \sqrt{x^{2} + 1}\right)$
2). $y = \cosh^{-1}(x) \leftrightarrow x = \cosh(y) = \frac{e^{y} + e^{-y}}{2} \rightarrow \cosh^{-1}(x) = \ln\left(x + \sqrt{x^{2} - 1}\right)$
3). $y = \tanh^{-1}(x) \leftrightarrow x = \tanh(y) = \frac{e^{y} - e^{-y}}{e^{y} + e^{-y}} \rightarrow \tanh^{-1}(x) = \frac{1}{2}\ln\left(\frac{1 + x}{1 - x}\right)$
정리3. 역쌍곡선 함수의 미분
1). $\frac{d}{dx} [\sinh^{-1}(x)] = \frac{1}{\sqrt{x^{2} + 1}}$
2). $\frac{d}{dx} [\cosh^{-1}(x)] = \frac{1}{\sqrt{x^{2} - 1}}$
3). $\frac{d}{dx} [\tanh^{-1}(x)] = \frac{1}{1 - x^{2}}$
설명
역쌍곡선 함수의 미분은 음함수 함수의 미분과 쌍곡선 함수의 정의를 적절히 활용하면 쉽게 증명할 수 있습니다.
$$\sinh^{-1}(x) = y \rightarrow \sinh(y) = x \rightarrow \cosh(y)\frac{dy}{dx} = 1 \rightarrow \frac{dy}{dx} = \frac{1}{\cosh(y)} = \frac{1}{\sqrt{1 + \sinh^{2}(x)}} = \frac{1}{\sqrt{1 + x^{2}}}$$
$$\cosh^{-1}(x) = y \rightarrow \cosh(y) = x \rightarrow \sinh(y)\frac{dy}{dx} = 1 \rightarrow \frac{dy}{dx} = \frac{1}{\sinh(y)} = \frac{1}{\sqrt{\cosh^{2}(x) - 1}} = \frac{1}{\sqrt{x^{2} - 1}}$$
$$\tanh^{-1}(x) = y \rightarrow \tanh(y) = x \rightarrow \text{sech}^{2}(y)\frac{dy}{dx} = 1 \rightarrow \frac{dy}{dx} = \frac{1}{\text{sech}^{2}(y)} = \frac{1}{1 - \tanh^{2}x} = \frac{1}{1 - x^{2}}$$
연습문제1. 각 쌍곡선 함수의 값을 구하여라.
(a). $\sinh (0)$
(b). $\tanh (0)$
(c). $\sinh(ln (2))$
(d). $\cosh (3)$
(e). $\text{sech} (0)$
(f). $\sinh (1)$
(a). $\sinh (0) = \frac{e^{0} - e^{0}}{2} = 0$
(b). $\tanh (0) = \frac{e^{0} - e^{0}}{\e^{0} + e^{0}} = 0$
(c). $\sinh(ln (2)) = \frac{e^{\ln (2)} - e^{-\ln (2)}}{2} = \frac{2 - \frac{1}{2}}{2} = \frac{3}{4}$
(d). $\cosh (3) = \frac{e^{3} + e^{-3}}{2}$
(e). $\text{sech} (0) = \frac{2}{e^{0} + e^{0}} = 1$
(f). $\sinh (1) = \frac{e^{1} - e^{-1}}{2}$
연습문제2. 각 쌍곡선 함수의 값을 구하여라.
(a). $\cosh (0)$
(b). $\tanh (1)$
(c). $\sinh (2)$
(d). $\cosh(\ln (3))$
(e). $\cosh^{-1} (1)$
(f). $\sinh^{-1} (1)$
(a). $\cosh (0) = \frac{e^{0} + e^{0}}{2} = 1$
(b). $\tanh (1) = \frac{e^{1} - e^{-1}}{e^{1} + e^{-1}}$
(c). $\sinh (2) = \frac{e^{2} - e^{-2}}{2}$
(d). $\cosh(\ln (3)) = \frac{e^{\ln (3)} - e^{-\ln (3)}}{2} = \frac{3 - \frac{1}{3}}{2} = \frac{4}{3}$
(e). $\cosh^{-1} (1) = 0$
(f). $\sinh^{-1} (1)$
$\sinh^{-1} (1) = a$라고 하자. 역함수와 쌍곡선 함수의 정의에 의해 $\sinh (a) = \frac{e^{a} - e^{-a}}{2} = 1$이므로 식을 아래와 같이 정리할 수 있다.
$$e^{2a} - 2e^{a} - 1 = 0 \rightarrow e^{a} = \frac{2 \pm \sqrt{5}}{2}$$
이때, $e^{a} > 0$이므로 $e^{a} = \frac{2 + \sqrt{5}}{2}$이다. 양변에 자연상수 $e$를 밑으로 하는 자연로그를 취하면 $a = \ln \left( \frac{2 + \sqrt{5}}{2} \right)$임을 알 수 있다.
연습문제3. 주어진 쌍곡선 함수들의 성질을 증명하시오.
(a). $\sinh(-x) = -\sinh(x)$
(b). $\cosh(-x) = \cosh(x)$
(c). $\cosh(x) + \sinh(x) = e^{x}$
(d). $\cosh(x) - \sinh(x) = e^{-x}$
(a). $\sinh(-x) = -\sinh(x)$
$$\begin{align*} \sinh (-x) &= \frac{e^{-x} - e^{-(-x)}}{2} \\ &= -\frac{e^{x} - e^{-x}}{2} = -\sinh(x) \end{align*}$$
(b). $\cosh(-x) = \cosh(x)$
$$\begin{align*} \cosh (-x) &= \frac{e^{-x} + e^{-(-x)}}{2} \\ &= \frac{e^{x} + e^{-x}}{2} = \cosh(x) \end{align*}$$
(c). $\cosh(x) + \sinh(x) = e^{x}$
$$\begin{align*} \cosh (x) + \sinh (x) &= \frac{e^{x} + e^{-x}}{2} + \frac{e^{x} - e^{-x}}{2} = e^{x} \end{align*}$$
(d). $\cosh(x) - \sinh(x) = e^{-x}$
$$\begin{align*} \cosh (x) - \sinh (x) &= \frac{e^{x} + e^{-x}}{2} - \frac{e^{x} - e^{-x}}{2} = e^{-x} \end{align*}$$
연습문제4. 주어진 쌍곡선 함수들의 성질을 증명하시오.
(a). $\coth^{2}(x) - 1 = \text{csch}^{2}(x)$
(b). $\tanh(x + y) = \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)}$
(c). $\sinh(2x) = 2\sinh(x)\cosh(x)$
(d). $\cosh(2x) = \cosh^{2}(x) + \sinh^{2}(x)$
(e). $\tanh(\ln(x)) = \frac{x^{2} - 1}{x^{2} + 1}$
(f). $\frac{1 + \tanh(x)}{1 - \tanh(x)} = e^{2x}$
(g). $(\cosh(x) + \sinh(x))^{n} = \cosh(nx) + \sinh(nx)$
(a). $\coth^{2}(x) - 1 = \text{csch}^{2}(x)$
$$\begin{align*} &\cosh^{2}(x) - \sinh^{2}(x) = 1 \\ \Rightarrow& \frac{\cosh^{2}(x)}{\sinh^{2}(x)} - 1 = \frac{1}{\sinh^{2}(x)} \\ \Rightarrow& \coth^{2}(x) - 1 = \text{csch}^{2}(x) \end{align*}$$
(b). $\tanh(x + y) = \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)}$
$$\begin{align*} \tanh(x + y) &= \frac{\sinh(x + y)}{\cosh(x + y)} \\ &= \frac{\sinh(x)\cosh(y) + \sinh(y)\cosh(x)}{\cosh(x)\cosh(y) + \sinh(x)\sinh(y)} \\ &= \frac{\frac{\sinh(x)}{\cosh(x)} + \frac{\sinh(y)}{\cosh(y)}}{1 + \left( \frac{\sinh(x)}{\cosh(x)} \right) \left( \frac{\sinh(y)}{\cosh(y)} \right)} \\ &= \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)} \end{align*}$$
(c). $\sinh(2x) = 2\sinh(x)\cosh(x)$
$$\begin{align*} \sinh(2x) &= \sinh(x + x) \\ &= \sinh(x)\cosh(x) + \sinh(x)cosh(x) \\ &= 2\sinh(x)\cosh(x) \end{align*}$$
(d). $\cosh(2x) = \cosh^{2}(x) + \sinh^{2}(x)$
$$\begin{align*} \cosh(2x) &= \cosh(x + x) \\ &= \cosh(x)\cosh(x) + \sinh(x)\sinh(x) \\ &= \cosh^{2}(x) + \sinh^{2}(x) \end{align*}$$
(e). $\tanh(\ln(x)) = \frac{x^{2} - 1}{x^{2} + 1}$
$$\begin{align*} \tanh(\ln(x)) &= \frac{e^{\ln(x)} - e^{-\ln(x)}}{e^{\ln(x)} + e^{-\ln(x)}} \\ &= \frac{x - \frac{1}{x}}{x + \frac{1}{x}} \\ &= \frac{x^{2} - 1}{x^{2} + 1} \end{align*}$$
(f). $\frac{1 + \tanh(x)}{1 - \tanh(x)} = e^{2x}$
$$\begin{align*} \frac{1 + \tanh(x)}{1 - \tanh(x)} &= \frac{1 + \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}}{1 - \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}} \\ &= \frac{(e^{x} + e^{-x}) + (e^{x} - e^{-x})}{(e^{x} + e^{-x}) - (e^{x} - e^{-x})} \\ &= \frac{2e^{x}}{e^{-x}} = e^{2x} \end{align*}$$
(g). $(\cosh(x) + \sinh(x))^{n} = \cosh(nx) + \sinh(nx)$
$$\begin{align*} (\cosh(x) + \sinh(x))^{n} &= \left( \frac{e^{x} + e^{-x}}{2} + \frac{e^{x} - e^{-x}}{2} \right)^{n} \\ &= [e^{x}]^{n} = e^{nx} \\ &= \frac{e^{nx} + e^{-nx}}{2} + \frac{e^{nx} - e^{-nx}}{2} \\ &= \cosh(nx) + \sinh(nx) \end{align*}$$
연습문제5. 각 쌍곡선 함수의 극한을 구하여라.
(a). $\lim_{x \rightarrow \infty} \tanh(x)$
(b). $\lim_{x \rightarrow \infty} \sinh(x)$
(c). $\lim_{x \rightarrow \infty} \text{sech}(x)$
(d). $\lim_{x \rightarrow 0^{+}} \coth(x)$
(a). $\lim_{x \rightarrow \infty} \tanh(x) = \lim_{x \rightarrow \infty} \left( \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} \right) = \lim_{x \rightarrow \infty} \left( \frac{1 - e^{-2x}}{1 + e^{-2x}} \right) = 1$
(b). $\lim_{x \rightarrow \infty} \sinh(x) = \lim_{x \rightarrow \infty} \frac{e^{x} - e^{-x}}{2} = \infty$
(c). $\lim_{x \rightarrow \infty} \text{sech}(x) = \lim_{x \rightarrow \infty} \frac{2}{e^{x} + e^{-x}} = 0$
(d). $\lim_{x \rightarrow 0^{+}} \coth(x) = \lim_{x \rightarrow 0^{+}} \frac{e^{x} + e^{-x}}{e^{x} - e^{-x}} = \infty$
연습문제6. 주어진 함수들의 도함수를 구하여라.
(a). $f(x) = \tanh(1 + e^{2x})$
(b). $g(x) = \cosh(\ln(x))$
(c). $y = x\coth(1 + x^{2})$
(d). $f(t) = \text{csch} (t) (1 - \ln (\text{csch}(t)))$
(e). $y = \sinh(\cosh(x))$
(f). $y = \sqrt[4]{\frac{1 + \tanh(x)}{1 - \tanh(x)}}$
(g). $y = x^{2}\sinh^{-1}(2x)$
(a). $f(x) = \tanh(1 + e^{2x})$
$$f^{'}(x) = 2e^{2x}\text{sech}^{2}(1 + e^{2x})$$
(b). $g(x) = \cosh(\ln(x))$
$$g^{'}(x) = \frac{\sinh(\ln(x))}{x}$$
(c). $y = x\coth(1 + x^{2})$
$$y^{'} = \coth(1 + x^{2}) - 2x^{2}\text{csch}^{2}(1 + x^{2})$$
(d). $f(t) = \text{csch} (t) (1 - \ln (\text{csch}(t)))$
$$\begin{align*} y^{'} &= -\text{csch}(t)\coth(t) (1 - \ln(\text{csch}(t))) + \text{csch}(x) \cdot \frac{\text{csch}(t)\coth(t)}{\text{csch}(t)} \\ &= -\text{csch}(t)\coth(t) + \text{csch}(t)\coth(t)\ln (\text{csch}(t)) + \text{csch}(t) \coth(t) \\ &= \text{csch}(t)\coth(t)\ln(\text{csch}(t))\end{align*}$$
(e). $y = \sinh(\cosh(x))$
$$\begin{align*} y^{'} &= -\sinh(x)\cosh(\cosh(x))\end{align*}$$
(f). $y = \sqrt[4]{\frac{1 + \tanh(x)}{1 - \tanh(x)}} = \sqrt[4]{e^{2x}} = e^{\frac{x}{2}}$
$$\begin{align*} y^{'} &= \frac{1}{2}e^{\frac{x}{2}} \end{align*}$$
(g). $y = x^{2}\sinh^{-1}(2x)$
$$\begin{align*} y^{'} &= 2x\sinh^{-1}(2x) + x^{2} \cdot \left( \frac{2}{\sqrt{1 + 4x^{2}}} \right) \\ &= 2x\sinh^{-1}(2x) + \frac{2x^{2}}{\sqrt{1 + 4x^{2}}}\end{align*}$$
연습문제7. 주어진 함수들의 도함수를 구하여라.
(a). $f(x) = x\sinh(x) - \cosh(x)$
(b). $h(x) = \ln (\cosh(x))$
(c). $y = e^{\cosh(3x)}$
(d). $f(t) = \text{sech}^{2}(e^{t})$
(e). $y = \arctan(\tanh(x))$
(f). $G(x) = \frac{1 - \cosh(x)}{1 + \cosh(x)}$
(g). $y = \tanh^{-1} (\sqrt{x})$
(a). $f(x) = x\sinh(x) - \cosh(x)$
$$\begin{align*} f^{'}(x) &= \sinh(x) + x\cosh(x) - \sinh(x) \\ &= x\cosh(x) \end{align*}$$
(b). $h(x) = \ln (\cosh(x))$
$$\begin{align*} h^{'}(x) &= \frac{\sinh(x)}{\cosh(x)} \\ &= \tanh(x) \end{align*}$$
(c). $y = e^{\cosh(3x)}$
$$\begin{align*} y^{'} &= 3\sinh(3x)e^{\cosh(3x)} \end{align*}$$
(d). $f(t) = \text{sech}^{2}(e^{t})$
$$\begin{align*} f^{'}(t) &= 2e^{t} \cdot (-\text{sech}(e^{t})\tanh(e^{t})) \text{sech}(e^{t}) \\ &= -2e^{t}\text{sech}^{2}(e^{t})\tanh(e^{t}) \end{align*}$$
(e). $y = \arctan(\tanh(x))$
$$\begin{align*} y^{'} &= \frac{\text{sech}^{2}(x)}{1 + \tanh^{2}(x)} \end{align*}$$
(f). $G(x) = \frac{1 - \cosh(x)}{1 + \cosh(x)}$
$$\begin{align*} G^{'}(x) &= \frac{-\sinh(x) (1 + \cosh(x)) - \sinh(x)(1 - \cosh(x))}{(1 + \cosh(x))^{2}} \\ &= -\frac{2\sinh(x)}{(1 + \cosh(x))^{2}}\end{align*}$$
(g). $y = \tanh^{-1} (\sqrt{x})$
$$\begin{align*} y^{'} &= \frac{1}{1 + (\sqrt{x})^{2}} \cdot \frac{1}{2\sqrt{x}} \\ &= \frac{1}{2\sqrt{x}(1 + x)}\end{align*}$$
연습문제8. 주어진 함수들의 도함수를 구하여라.
(a). $y = x\tanh^{-1}(x) + \ln (\sqrt{1 - x^{2}})$
(b). $y = x\sinh^{-1} \left( \frac{x}{3} \right) - \sqrt{9 + x^{2}}$
(c). $y = \text{sech}^{-1} (\sqrt{1 - x^{2}}), x > 0$
(d). $y = \coth^{-1}(\sqrt{x^{2} + 1})$
(a). $y = x\tanh^{-1}(x) + \ln (\sqrt{1 - x^{2}})$
$$\begin{align*} y^{'} &= \tanh^{-1}(x) + \frac{x}{1 + x^{2}} + \frac{1}{1 - x^{2}} \cdot \left( \frac{-2x}{2\sqrt{1 - x^{2}}} \right) \\ &= \tanh^{-1}(x) + \frac{x}{1 + x^{2}} - \frac{x}{\sqrt{1 - x^{2}}}\end{align*}$$
(b). $y = x\sinh^{-1} \left( \frac{x}{3} \right) - \sqrt{9 + x^{2}}$
$$\begin{align*} y^{'} &=\sinh^{-1} \left( \frac{x}{3} \right) + x \cdot \frac{\frac{1}{3}}{\sqrt{1 - \left( \frac{x}{3} \right)^{2}}} - \frac{2x}{2\sqrt{9 + x^{2}}} \\ &= \sinh^{-1} \left( \frac{x}{3} \right) + \frac{x}{\sqrt{9 - x^{2}}} - \frac{x}{\sqrt{9 + x^{2}}}\end{align*}$$
(c). $y = \text{sech}^{-1} (\sqrt{1 - x^{2}}), x > 0$
$$\begin{align*} y^{'} &= \frac{-2x}{2\sqrt{1 - x^{2}}} \cdot \frac{1}{\sqrt{1 - (\sqrt{1 - x^{2}})^{2}}} \\ &= -\frac{x}{\sqrt{1 - x^{2}}} \cdot \frac{1}{x} \\ &= -\frac{1}{\sqrt{1 - x^{2}}} \end{align*}$$
(d). $y = \coth^{-1}(\sqrt{x^{2} + 1})$
$$\begin{align*} y^{'} &= \frac{2x}{2\sqrt{1 + x^{2}}} \cdot \frac{1}{1 - (\sqrt{1 + x^{2}})^{2}} \\ &= \frac{x}{\sqrt{1 + x^{2}}} \cdot \left( -\frac{1}{x^{2}} \right) \\ &= -\frac{1}{x\sqrt{x^{2} + 1}}\end{align*}$$
연습문제9. $\lim_{x \rightarrow \infty} \frac{\sinh(x)}{e^{x}}$를 구하여라.
$$\begin{align*} \lim_{x \rightarrow \infty} \frac{\sinh(x)}{e^{x}} &= \lim_{x \rightarrow \infty} \frac{e^{x} - e^{-x}}{2e^{x}} \\ &= \lim_{x \rightarrow \infty} \frac{1}{2} (1 - e^{-2x}) = \frac{1}{2} \end{align*}$$
연습문제10. $x = \ln(\sec(\theta) + \tan(\theta))$일 때, $\sec(\theta) = \cosh(x)$임을 보여라.
$x = \ln (\sec(\theta) + \tan(\theta))$이므로 $e^{x} = \sec(\theta) + \tan(\theta) = \frac{1 + \sin(\theta)}{\cos(\theta)}$이다. 이와 동일한 방법으로 양변에 음수를 취하고 자연상수를 취해주면 $e^{-x} = \frac{\cos(\theta)}{1 + \sin(\theta)}$를 얻을 수 있다.
$$\begin{align*} e^{x} + e^{-x} &= \frac{1 + \sin(\theta)}{\cos(\theta)} + \frac{\cos(\theta)}{1 + \sin(\theta)} \\ &= \frac{(1 + \sin(\theta))^{2} + \cos^{2}(\theta)}{\cos(\theta)(1 + \sin(\theta))} \\ &= \frac{1 + 2\sin(\theta) + (\sin^{2}(\theta) + \cos^{2}(\theta))}{\cos(\theta)(1 + \sin(\theta))} \\ &= \frac{2(1 + \sin(\theta))}{\cos(\theta) (1 + \sin(\theta))} \\ &= \frac{2}{\cos(\theta)} = 2\sec(\theta) \end{align*}$$
따라서, $\sec(\theta) = \frac{e^{x} + e^{-x}}{2} = \cosh(x)$이다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.09.21 : 연습문제1-5 추가
22.09.22 : 연습문제6-10 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 적분 연습문제 (0) | 2022.11.30 |
|---|---|
| 미적분학 - 미분 규칙 연습문제 (0) | 2022.09.22 |
| 미적분학 - 목차 (0) | 2022.08.03 |
| 미적분학 - 발산 정리 (0) | 2022.08.02 |
| 미적분학 - 스토크스의 정리 (0) | 2022.08.01 |
