안녕하세요. 지난 포스팅의 미적분학 - 매개변수 함수에서는 매개변수가 포함된 간단한 함수들의 정의와 유명한 사이클로이드(cycloid) 함수까지 매개변수로 표현해보았습니다. 오늘은 매개변수 함수에서 미적분학을 어떻게 적용할 수 있는 지 알아보도록 하겠습니다.
미적분학 - 매개변수 함수
안녕하세요. 지난 포스팅의 미적분학 - 일에서는 적분을 물리학에 응용하는 방법에 대해서 알아보았습니다. 지금까지 저희는 극한, 미분, 적분을 통해 기본적인 미적분학의 지식은 갖추었습니
everyday-image-processing.tistory.com
1. 기울기(Tangent)
매개변수 함수에서는 $x = f(t), y = g(t)$로 표현될 수 있다고 하였습니다. 그리고 만약, 매개변수 $t$를 소거할 수 있다면 $y = F(x)$의 꼴로 나타낼 수 있겠죠.
$$y = F(x) \Rightarrow g(t) = F(f(t))$$
따라서, $g, f, F$가 모두 미분가능하다면 미적분학 - 연쇄 법칙에서 보았던 연쇄 법칙을 이용해서 아래와 같이 미분할 수 있습니다.
$$g^{'}(t) = F^{'}(f(t))f^{'}(t) = F^{'}(x)f^{'}(t)$$
여기서 $f^{'}(t) \neq 0$이라면 $F^{'}(x) = \frac{g^{'}(t)}{f^{'}(t)}$를 통해 매개변수 함수 꼴의 미분을 구할 수 있습니다. 만약, 라이브니츠 표기법(Leibniz Notation)을 이용해서 표현하면 아래와 같습니다.
$$\frac{dy}{dx} = \frac{dy / dt}{dx / dt}$$
이제, 고계도미분까지 해볼까요? 이 역시 정의를 이용하면 쉽게 할 수 있습니다.
$$\frac{d^{2}y}{dx^{2}} = \frac{d}{dx} \left(\frac{dy}{dx}\right) = \frac{\frac{d}{dt} \left(\frac{dy}{dx}\right)}{\frac{dx}{dt}}$$
예제1. $\theta = \frac{\pi}{3}$에서 사이클로이드 곡선 $x = r(\theta - \sin(\theta)), y = r(1 - \cos(\theta))$의 기울기를 구하여라.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy/d\theta}{dx/d\theta} \\ &= \frac{\sin(\theta)}{1 - \cos(\theta)} \end{align*}$$
따라서, $\theta = \frac{\pi}{3}$에서 사이클로이드 곡선의 기울기는 $\frac{dy}{dx}_{\theta = \frac{\pi}{3}} = \frac{\sin(\frac{\pi}{3})}{1 - \cos(\frac{\pi}{3})} = \sqrt{3}$이다.
2. 영역의 넓이(Area)
다음으로 넓이입니다. 저희가 미적분학 - 두 곡선 사이의 넓이에서 보았던 식에 의하면 $y = F(x)$가 주어졌을 때, 닫힌 구간 $[a, b]$로 둘러쌓인 영역의 넓이는 $A = \int_{a}^{b} F(x) \; dx$로 구할 수 있었습니다. 하지만, $x = f(t), y = g(t)$와 같이 매개변수로 주어져있을 때는 어떻게 계산할 수 있을까요? 전혀 어렵지 않으니 천천히 보시길 바랍니다. 일단, $\alpha \le t \le \beta$에서 정의되었다고 가정하겠습니다. 그리고 $F(x) = y = g(t)$이고 $x = f(t) \Rightarrow dx = f^{'}(t) dt$입니다. 따라서, 아래와 같이 계산하면 원하는 영역의 넓이를 구할 수 있습니다.
$$A = \int_{a}^{b} y \; dx = \int_{\alpha}^{\beta} g(t) f^{'}(t) \; dt$$
예제2. 사이클로이드 곡선 $x = r(\theta - \sin(\theta)), y = r(1 - \cos(\theta))$의 한 주기에 해당하는 넓이를 구하여라.
사이클로이드 곡선의 한 주기는 $0 \le \theta \le 2 \pi$이고 $dx = r(1 - \cos(\theta))$이기 때문에 아래와 같이 적분가능하다.
$$\begin{align*} A &= \int_{0}^{2\pi} r(1 - \cos(\theta)) \cdot r(1 - \cos(\theta)) \; d\theta \\ &= r^{2} \int_{0}^{2\pi} (1 - \cos(\theta))^{2} \; d\theta \\ &= r^{2} \int_{0}^{2\pi} (1 - 2\cos(\theta) + \cos^{2}(\theta)) \; d\theta \\ &= r^{2} \int_{0}^{2 \pi} (1 - 2\cos(\theta) + \left(\frac{1 + \cos(2\theta)}{2}\right)) \; d\theta \\ &= r^{2} \left[\frac{3}{2}\theta -2\sin(\theta) + \frac{1}{4}\sin(2\theta)\right]_{0}^{2\pi} \\ &= r^{2} \frac{3}{2} \cdot 2 \pi = 3r^{2}\pi \end{align*}$$
3. 곡선의 길이 (Arc Length)
함수 $y = F(x)와 구간 $a \le x \le b$로 둘러쌓인 곡선 $C$의 길이를 구하는 방법은 미적분학 - 곡선의 길이에서 알아보았습니다. 그 결과 아래의 식을 통해서 구할 수 있었죠.
$$L = \int_{a}^{b} \sqrt{1 + \left(\frac{dy}{dx}\right)^{2}} \; dx$$
이제부터는 곡선 $C$가 매개변수 함수의 꼴로 $x = f(t), y = g(t)$로 주어졌다고 가정하겠습니다. 그리고 $t$의 범위는 $\alpha \le t \le \beta$입니다.
$$L = \int_{a}^{b} \sqrt{1 + \left(\frac{dy / dt}{dx / dt}\right)^{2}} \; \frac{dx}{dt} dt = \int_{\alpha}^{\beta} \sqrt{\left(\frac{dx}{dt}\right)^{2} + \left(\frac{dy}{dt}\right)^{2}} \; dt$$
예제1. $0 \le t \le 2\pi$일 때, $x = \cos(t), y = \sin(t)$로 이루어지는 곡선의 자취의 길이를 구하여라.
$\frac{dx}{dt} = -\sin(t), \frac{dy}{dt} = \cos(t)$이기 때문에 아래와 같이 적분 가능하다.
$$L = \int_{0}^{2\pi} \sqrt{\sin^{2}(t) + \cos^{2}(t)} \; dt = \int_{0}^{2\pi} 1 \; dt = \left[t\right]_{0}^{2\pi} = 2\pi$$
예제2. 사이클로이드 곡선 $x = r(\theta - \sin(\theta)), y = r(1 - \cos(\theta))$의 한 주기에 해당하는 곡선의 길이를 구하여라.
$\frac{dx}{d\theta} = r(1 - \cos(\theta)), \frac{dy}{d\theta} = r\sin(\theta)$이기 때문에 아래와 같이 적분 가능하다.
$$\begin{align*} L &= \int_{0}^{2\pi} \sqrt{\left[r(1 - \cos(\theta))\right]^{2} + \left[r\sin(\theta)\right]^{2}} \; dt \\ &= \int_{0}^{2\pi} \sqrt{r^{2}(1 - \cos(\theta))^{2} + r^{2}\sin^{2}(\theta)} \; dt \\ &= r\int_{0}^{2\pi} \sqrt{1 - 2\cos(\theta) + \cos^{2}(\theta) + \sin^{2}(\theta)} \; dt \\ &= r \int_{0}^{2\pi} \sqrt{2(1 - \cos(\theta))} \; dt \\ &= r \int_{0}^{2\pi} \sqrt{4\sin^{2}(\frac{\theta}{2})} \; dt \\ &= r\int_{0}^{2\pi} 2\sin\left(\frac{\theta}{2}\right) \; dt\\ &= 2r \left[-2\cos\left(\frac{\theta}{2}\right)\right]_{0}^{2\pi} \\ &= 2r(2 + 2) = 8r\end{align*}$$
4. 곡면의 겉넓이 (Surface Area)
곡면의 겉넓이 역시 쉽게 공식을 바꾸어서 해결할 수 있습니다.
$$S = \int_{\alpha}^{\beta} 2\pi y \sqrt{\left(\frac{dx}{dt}\right)^{2} + \left(\frac{dy}{dt}\right)^{2}} \; dt $$
연습문제1. 주어진 매개변수 곡선의 기울기 $\frac{dy}{dx}$를 구하여라.
(a). $x = t\sin(t), y = t^{2} + t$
(b). $x = \frac{1}{t}, y = \sqrt{t}e^{-t}$
(a). $x = t\sin(t), y = t^{2} + t$
매개변수 곡선의 기울기는 $\frac{dy}{dx} = \frac{dy / dt}{dx / dt}$이므로 먼저 $\frac{dy}{dt}$ 그리고 $\frac{dx}{dt}$를 구한다.
$$\begin{cases} \frac{dy}{dt} &= 2t + 1 \\ \frac{dx}{dt} &= \sin(t) + t\cos(t) \end{cases}$$
따라서, 주어진 곡선의 기울기는 다음과 같이 구할 수 있다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / dt}{dx / dt} \\ &= \frac{2t + 1}{\sin(t) + t\cos(t)} \end{align*}$$
(b). $x = \frac{1}{t}, y = \sqrt{t}e^{-t}$
매개변수 곡선의 기울기는 $\frac{dy}{dx} = \frac{dy / dt}{dx / dt}$이므로 먼저 $\frac{dy}{dt}$ 그리고 $\frac{dx}{dt}$를 구한다.
$$\begin{cases} \frac{dy}{dt} &= \frac{1}{\sqrt{t}}e^{-t} - \sqrt{t}e^{-t} = \left( \frac{1}{2\sqrt{t}} - \sqrt{t} \right) e^{-t} \\ \frac{dx}{dt} &= -\frac{1}{t^{2}} \end{cases}$$
따라서, 주어진 곡선의 기울기는 다음과 같이 구할 수 있다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / dt}{dx / dt} \\ &= \frac{\left( \frac{1}{2\sqrt{t}} - \sqrt{t} \right) e^{-t}}{-\frac{1}{t^{2}}} \\ &= t^{\frac{3}{2}} \left( t - \frac{1}{2} \right) e^{-t} \end{align*}$$
연습문제2. 매개변수 곡선과 점이 주어졌을 때 해당 점에서 접선의 방정식을 구하여라.
(a). $x = t^{4} + 1, y = t^{3} + t, t = -1$
(b). $x = t - \frac{1}{t}, y = 1 + t^{2}, t = 1$
(c). $x = e^{\sqrt{t}}, y = t - \ln t^{2}, t = 1$
(d). $x = \cos (\theta) + 2\sin(2\theta), y = \sin(\theta) + \cos(2\theta), \theta = 0$
(a). $x = t^{4} + 1, y = t^{3} + t, t = -1$
먼저 주어진 매개변수 곡선에 대해 점 $t = -1$에서의 접선의 기울기를 구한다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / dt}{dx / dt} \\ &= \frac{3t^{2} + 1}{4t^{3}} \end{align*}$$
위 식에 $t = -1$을 대입하면 접선의 기울기가 -1임을 알 수 있다. 이때, $t = -1$을 두 매개변수 방정식 $x(t)$와 $y(t)$에 대입하면 해당 시점에서 접선이 지나는 점이 $(2, -2)$임을 알 수 있다. 따라서, 해당 매개변수 곡선 $(x(t), y(t))$가 시점 $t = -1$에서의 접선의 방정식은 다음과 같다.
$$y = - (x - 2) - 2 = -x$$
(b). $x = t - \frac{1}{t}, y = 1 + t^{2}, t = 1$
먼저 주어진 매개변수 곡선에 대해 점 $t = 1$에서의 접선의 기울기를 구한다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / dt}{dx / dt} \\ &= \frac{2t}{1 + \frac{1}{t^{2}}} \end{align*}$$
위 식에 $t = 1$을 대입하면 접선의 기울기가 1임을 알 수 있다. 이때, $t = 1$을 두 매개변수 방정식 $x(t)$와 $y(t)$에 대입하면 해당 시점에서 접선이 지나는 점이 $(0, 2)$임을 알 수 있다. 따라서, 해당 매개변수 곡선 $(x(t), y(t))$가 시점 $t = 1$에서의 접선의 방정식은 다음과 같다.
$$y = (x - 0) + 2 = x + 2$$
(c). $x = e^{\sqrt{t}}, y = t - \ln t^{2}, t = 1$
먼저 주어진 매개변수 곡선에 대해 점 $t = 1$에서의 접선의 기울기를 구한다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / dt}{dx / dt} \\ &= \frac{1 - \frac{2}{t}}{\frac{1}{2\sqrt{t}}e^{\sqrt{t}}} \end{align*}$$
위 식에 $t = 1$을 대입하면 접선의 기울기가 $-\frac{2}{e}$임을 알 수 있다. 이때, $t = 1$을 두 매개변수 방정식 $x(t)$와 $y(t)$에 대입하면 해당 시점에서 접선이 지나는 점이 $(e, 1)$임을 알 수 있다. 따라서, 해당 매개변수 곡선 $(x(t), y(t))$가 시점 $t = 1$에서의 접선의 방정식은 다음과 같다.
$$y = -\frac{2}{e}(x - e) + 1 = -\frac{2}{e} x + 3$$
(d). $x = \cos (\theta) + 2\sin(2\theta), y = \sin(\theta) + \cos(2\theta), \theta = 0$
먼저 주어진 매개변수 곡선에 대해 점 $\theta = 0$에서의 접선의 기울기를 구한다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / d\theta}{dx / d\theta} \\ &= \frac{\cos(\theta) - 2\sin(2\theta)}{-\sin(\theta) + 2\cos(2\theta)} \end{align*}$$
위 식에 $\theta = 0$을 대입하면 접선의 기울기가 $\frac{1}{2}$임을 알 수 있다. 이때, $\theta = 1$을 두 매개변수 방정식 $x(\theta)$와 $y(\theta)$에 대입하면 해당 시점에서 접선이 지나는 점이 $(1, 1)$임을 알 수 있다. 따라서, 해당 매개변수 곡선 $(x(\theta), y(\theta))$가 시점 $\theta = 1$에서의 접선의 방정식은 다음과 같다.
$$y = \frac{1}{2}(x - 1) + 1 = \frac{1}{2} x + \frac{1}{2}$$
연습문제3. 매개변수 곡선과 점이 주어졌을 때 해당 점에서 접선의 방정식을 구하여라.
(a). $x = 1 + \ln (t), y = t^{2} + 2, (1, 3)$
(b). $x = \tan (\theta), y = \sec (\theta), (1, \sqrt{2})$
(a). $x = 1 + \ln (t), y = t^{2} + 2, (1, 3)$
먼저 주어진 매개변수 곡선에 대해 점 $(1, 3)$에서의 접선의 기울기를 구한다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / dt}{dx / dt} \\ &= \frac{2t}{\frac{1}{t}} \\ &= 2t^{2} \\ &= 2 (y - 2) \end{align*}$$
위 식에 $y = 3$을 대입하면 접선의 기울기가 2임을 알 수 있다. 따라서, 해당 매개변수 곡선 $(x(t), y(t))$가 점 $(1, 3)$에서의 접선의 방정식은 다음과 같다.
$$y = 2 (x - 1) + 3 = 2x + 1$$
(b). $x = \tan (\theta), y = \sec (\theta), (1, \sqrt{2})$
먼저 주어진 매개변수 곡선에 대해 점 $\theta = 0$에서의 접선의 기울기를 구한다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / d\theta}{dx / d\theta} \\ &= \frac{\sec(\theta)\tan(\theta)}{\sec^{2} (\theta)} \\ &= \frac{\tan(\theta)}{\sec(\theta)} \\ &= \frac{x}{y} \end{align*}$$
위 식에 $(x, y) = (1, \sqrt{2})$을 대입하면 접선의 기울기가 $\frac{1}{\sqrt{2}}$임을 알 수 있다. 따라서, 해당 매개변수 곡선 $(x(t), y(t))$가 점 $(1, \sqrt{2})$에서의 접선의 방정식은 다음과 같다.
$$y = \frac{1}{\sqrt{2}}(x - 1) + \sqrt{2}$$
연습문제4. 주어진 매개변수 곡선의 2차 미분 $\frac{d^{2}y}{dx^{2}}$를 구하여라.
(a). $x = 4 + t^{2}, y = t^{2} + t^{3}$
(b). $x = t^{3} - 12t, y = t^{2} - 1$
(c). $x = t - e^{t}, y = t + e^{-t}$
(d). $x = t + \ln (t), y = t - \ln (t)$
(e). $x = 2 \sin(t), y = 3 \cos(t), 0 < t < 2\pi$
(f). $x = \cos(2t), y = \cos(t), 0 < t < \pi$
(a). $x = 4 + t^{2}, y = t^{2} + t^{3}$
매개변수 곡선의 2차 미분은 $\frac{d^{2}y}{dx^{2}} = \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right)$이므로 다음과 같이 구할 수 있다.
$$\begin{align*} \frac{d^{2} y }{dx^{2}} &= \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{2t + 3t^{2}}{2t} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{1 + 3t}{2} \right) \\ &= \frac{3 / 2}{2t} = \frac{3}{4}t \end{align*}$$
(b). $x = t^{3} - 12t, y = t^{2} - 1$
매개변수 곡선의 2차 미분은 $\frac{d^{2}y}{dx^{2}} = \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right)$이므로 다음과 같이 구할 수 있다.
$$\begin{align*} \frac{d^{2} y }{dx^{2}} &= \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{2t}{3t^{2} - 12} \right) \\ &= \frac{2(3t^{2} - 12) - 2t \cdot 6t}{(3t^{2} - 12)^{2}} \cdot \frac{1}{3t^{2} - 12} \\ &= \frac{6t^{2} - 24 - 12t^{2}}{(3t^{2} - 12)^{3}} \\ &= \frac{-6 (t^{2} + 4)}{27 (t^{2} - 4)^{3}} \\ &= -\frac{2 (t^{2} + 4)}{9 (t^{2} - 4)^{3}} \end{align*}$$
(c). $x = t - e^{t}, y = t + e^{-t}$
매개변수 곡선의 2차 미분은 $\frac{d^{2}y}{dx^{2}} = \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right)$이므로 다음과 같이 구할 수 있다.
$$\begin{align*} \frac{d^{2} y }{dx^{2}} &= \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{1 - e^{-t}}{1 - e^{t}} \right) \\ &= \frac{e^{-t} (1 - e^{t}) + e^{t}(1 - e^{-t})}{(1 - e^{t})^{2}} \cdot \frac{1}{1 - e^{t}} \\ &= \frac{e^{-t} - 1 + e^{t} - 1}{(1 - e^{t})^{3}} \\ &= \frac{e^{-t} + e^{t} - 2}{(1 - e^{t})^{3}} \end{align*}$$
(d). $x = t + \ln (t), y = t - \ln (t)$
매개변수 곡선의 2차 미분은 $\frac{d^{2}y}{dx^{2}} = \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right)$이므로 다음과 같이 구할 수 있다.
$$\begin{align*} \frac{d^{2} y }{dx^{2}} &= \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{1 + \frac{1}{t}}{1 - \frac{1}{t}} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{t + 1}{t - 1} \right) \\ &= \frac{(t - 1) - (t + 1)}{(t - 1)^{2}} \cdot \frac{t}{t - 1} \\ &= \frac{-2t}{(t - 1)^{3}} \end{align*}$$
(e). $x = 2 \sin(t), y = 3 \cos(t), 0 < t < 2\pi$
매개변수 곡선의 2차 미분은 $\frac{d^{2}y}{dx^{2}} = \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right)$이므로 다음과 같이 구할 수 있다.
$$\begin{align*} \frac{d^{2} y }{dx^{2}} &= \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{-3\sin(t)}{2\cos(t)} \right) \\ &= \frac{-3\cos(t) \cdot 2\cos(t) + (-3\sin(t)) \cdot (-2\sin(t))}{4\cos^{2}(t)} \cdot \frac{1}{2\cos(t)} \\ &= \frac{-6 (\sin^{2} (t) + \cos^{2} (t))}{4\cos^{2} (t)} \cdot \frac{1}{2\cos(t)} \\ &= \frac{-6}{4\cos^{2} (t)} \cdot \frac{1}{2\cos(t)} \\ &= -\frac{3}{4\cos^{3}(t)} \end{align*}$$
(f). $x = \cos(2t), y = \cos(t), 0 < t < \pi$
매개변수 곡선의 2차 미분은 $\frac{d^{2}y}{dx^{2}} = \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right)$이므로 다음과 같이 구할 수 있다.
$$\begin{align*} \frac{d^{2} y }{dx^{2}} &= \frac{d / dt}{dx / dt} \left( \frac{dy / dt}{dx / dt} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{-\sin(t)}{-2\sin(2t)} \right) \\ &= \frac{d / dt}{dx / dt} \left( \frac{\sin(t)}{4\sin(t)\cos(t)} \right) \\ &= \frac{d /dt}{dx / dt} \left( \frac{1}{4\cos(t)} \right) \\ &= -\frac{\sin(t)}{4\cos^{2}(t)} \cdot \frac{1}{-2\sin(2t)} \\ &= \frac{\sin(t)}{4\cos^{2} (t)} \cdot \frac{1}{4\sin(t)\cos(t)} \\ &= \frac{1}{16\cos^{3} (t)} \end{align*}$$
연습문제5. 주어진 매개변수 곡선에서 접선이 수직 또는 수평인 점을 찾아라.
(a). $x = 10 - t^{2}, y = t^{3} - 12t$
(b). $x = 2t^{3} + 3t^{2} - 12t, y = 2t^{3} + 3t^{2} + 1$
(a). $x = 10 - t^{2}, y = t^{3} - 12t$
매개변수 곡선의 기울기 $\frac{dy}{dx} = \frac{dy / dt}{dx / dt}$를 먼저 구한다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / dt}{dx / dt} \\ &= \frac{3t^{2} - 12}{-2t} \\ &= \frac{3 (t - 2) (t + 2)}{-2t} \end{align*}$$
1). 접선이 수평인 경우
위 식에서 $\frac{3(t - 2)(t + 2)}{-2t} = 0$이라고 할 때 $t = 2$ 그리고 $t = -2$일 때 접선이 0이므로 두 점 $(6, -16)$ 그리고 $(6, 16)$에서 수평이다.
2). 접선이 수직인 경우
위 식에서 $t = 0$일 때 기울기가 무한대로 발산하므로 점 $(10, 0)$에서 수직이다.
(b). $x = 2t^{3} + 3t^{2} - 12t, y = 2t^{3} + 3t^{2} + 1$
매개변수 곡선의 기울기 $\frac{dy}{dx} = \frac{dy / dt}{dx / dt}$를 먼저 구한다.
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / dt}{dx / dt} \\ &= \frac{6t^{2} + 6t}{6t^{2} + 6t - 12} \\ &= \frac{t(t + 1)}{(t + 2)(t - 1)} \end{align*}$$
1). 접선이 수평인 경우
위 식에서 $\frac{t(t + 1)}{(t + 2)(t - 1)} = 0$이라고 할 때 $t = 0$ 그리고 $t = -1$일 때 접선이 0이므로 두 점 $(0, 1)$ 그리고 $(13, 2)$에서 수평이다.
2). 접선이 수직인 경우
위 식에서 $t = -2$ 그리고 $t = 1$일 때 기울기가 무한대로 발산하므로 점 $(20, -3)$ 그리고 $(-7, 6)$에서 수직이다.
연습문제6. 타원의 매개변수 방정식 $x = a\cos(\theta), y = b\sin(\theta), 0 \le \theta \le 2\pi$를 이용하여 내부 넓이를 구하여라.
타원의 특징 중 하나는 원점을 중심으로 가지는 타원의 특징 중 하나는 각 사분면의 해당하는 넓이가 동일하다는 것이다. 이를 이용하여 $0 \le \theta \le 2\pi$까지에 해당되는 넓이를 구하는 것이 아닌 제 1사분면인 $0 \le \theta \le \frac{\pi}{2}$에 해당하는 타원의 넓이를 구한 뒤 4를 곱해준다.
먼저 $\theta = 0$이면 $x = a, y = 0$이다. 그리고 $\theta = \frac{\pi}{2}$이면 $x = 0, y = a$이다. 따라서, 타원 내부의 전체 넓이는 다음과 같이 구할 수 있다. 여기서 주의해야할 점은 $x$에 대해 적분을 수행 시 $x = 0 \rightarrow x = a$는 $\theta = \frac{\pi}{2} \rightarrow \theta = 0$이라는 점이다.
$$\begin{align*} A &= 4 \int_{\frac{\pi}{2}}^{0} y dx \\ &= 4 \int_{\frac{\pi}{2}}^{0} b\sin(\theta) (-a\sin(\theta)) \; d\theta \\ &= 4ab \int_{0}^{\frac{\pi}{2}} \sin^{2} (\theta) \; d\theta \\ &= 4ab \int_{0}^{\frac{\pi}{2}} \frac{1 - \cos(2\theta)}{2} \; d\theta \\ &= 2ab \int_{0}^{\frac{\pi}{2}} (1 - 2\cos(2\theta)) \; d\theta \\ &= 2ab \left[ \theta - \sin(2\theta) \right]_{0}^{\frac{\pi}{2}} = 2ab \left( \frac{\pi}{2} \right) = ab \pi \end{align*}$$
연습문제7. 매개변수 곡선 $x = t^{2} - 2t, y = \sqrt{t}$ 그리고 $y$-축으로 둘러쌓인 영역의 넓이를 구하여라.
문제를 해결하기 위해 주어진 곡선의 넓이를 그린다. (편의를 위해 WolframAlpha 이용하였습니다.)
STEP1. 주어진 매개변수 함수 그리기
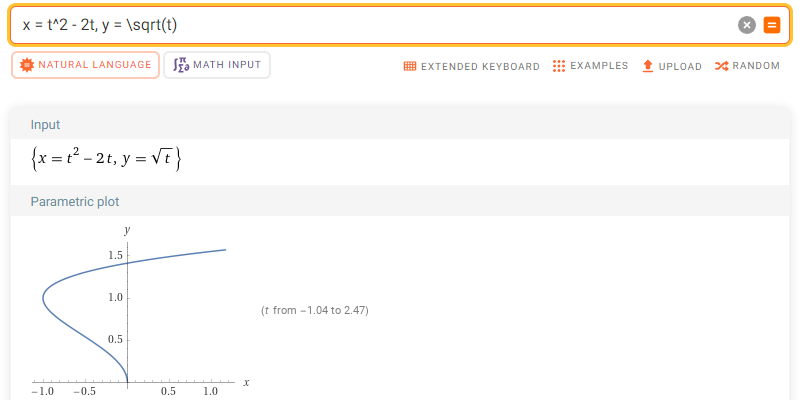
위 그림에서 $y$-축도 함께 둘러쌓인 영역을 확인할 수 있다.
STEP2. 해당 영역에 대한 넓이 공식 적용
이때, $y$-축으로 둘러쌓인 영역이기 때문에 $x \le 0$인 영역에 대한 적분으로 이할 수 있다. 따라서, $x = t^{2} - 2t = t(t - 2)\le 0$인 영역을 의미하기 때문에 $0 \le t \le 2$에서의 넓이를 구하는 것과 같다.
$$\begin{align*} A &= \int_{0}^{2} x \; dy \\ &= \int_{0}^{2} (t^{2} -2t) \frac{1}{2\sqrt{t}} \; dt \\ &= \frac{1}{2} \int_{0}^{2} (t^{\frac{3}{2}} - 2t^{\frac{1}{2}}) \; dt \\ &= \frac{1}{2} \left[ \frac{2}{5}t^{\frac{5}{2}} - \frac{4}{3} t^{\frac{3}{2}} \right]_{0}^{2} \\ &= \frac{1}{2} \cdot \left( \frac{4\sqrt{2}}{5} - \frac{4\sqrt{2}}{3} \right) = \frac{8\sqrt{2}}{15} \end{align*}$$
연습문제8. 매개변수 곡선 $x = 1 + e^{t}, y = t - t^{2}$ 그리고 $x$-축으로 둘러쌓인 영역의 넓이를 구하여라.
문제를 해결하기 위해 주어진 곡선의 넓이를 그린다. (편의를 위해 WolframAlpha 이용하였습니다.)
STEP1. 주어진 매개변수 함수 그리기
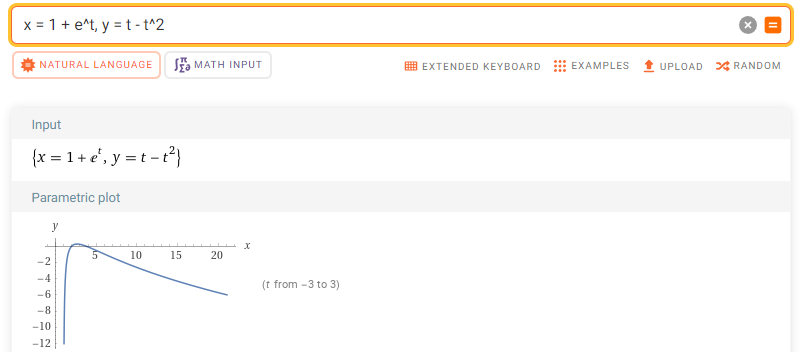
위 그림에서 아주 조금 $x$-축도 함께 둘러쌓인 영역을 확인할 수 있다.
STEP2. 해당 영역에 대한 넓이 공식 적용
이때, $x$-축으로 둘러쌓인 영역이기 때문에 $y \ge 0$인 영역에 대한 적분으로 이할 수 있다. 따라서, $y = t - t^{2} = t(1 - t)\le 0$인 영역을 의미하기 때문에 $0 \le t \le 1$에서의 넓이를 구하는 것과 같다.
$$\begin{align*} A &= \int_{0}^{1} y \; dx \\ &= \int_{0}^{1} (t - t^{2}) e^{t} \; dt \\ &= \int_{0}^{1} (t e^{t} - t^{2} e^{t}) \; dt \end{align*}$$
위 수식의 두 적분 항에 대해 각각 부분적분법을 적용하여 전개한다.
1). $\int_{0}^{1} t e^{t} \; dt$
$f(t) = t$ 그리고 $g^{'} (t) = e^{t}$라고 하자. 따라서 $f^{'}(x) = 1$ 이고 $g(x) = e^{t}$이다. 부분적분을 통해 아래와 같이 적분할 수 있다.
$$\begin{align*} \int_{0}^{1} t e^{t} \; dt &= \int f(t) g^{'}(t) \; dx \\ &= \left[ f(t) g(t) \right]_{0}^{1} - \int_{0}^{1} f^{'}(t) g(t) \; dt \\ &= \left[ t e^{t} \right]_{0}^{1} - \int_{0}^{1} e^{t} \; dt \\ &= e - \left[ e^{t} \right]_{0}^{1} \\ &= e - (e - 1) = 1 \end{align*}$$
2). $\int_{0}^{1} t^{2} e^{t} \; dt$
$f(t) = t^{2}$ 그리고 $g^{'} (t) = e^{t}$라고 하자. 따라서 $f^{'}(x) = 2t$ 이고 $g(x) = e^{t}$이다. 부분적분을 통해 아래와 같이 적분할 수 있다.
$$\begin{align*} \int_{0}^{1} t^{2} e^{t} \; dt &= \int f(t) g^{'}(t) \; dx \\ &= \left[ f(t) g(t) \right]_{0}^{1} - \int_{0}^{1} f^{'}(t) g(t) \; dt \\ &= \left[ t^{2} e^{t} \right]_{0}^{1} - \int_{0}^{1} 2t e^{t} \; dt = e - 2 \end{align*}$$
따라서 1)과 2)의 결과를 합치면 주어진 매개변수의 영역에 대한 넓이는 다음과 같이 구할 수 있다.
$$\begin{align*} A &= \int_{0}^{1} y \; dx \\ &= \int_{0}^{1} (t - t^{2}) e^{t} \; dt \\ &= \int_{0}^{1} (t e^{t} - t^{2} e^{t}) \; dt \\ &= \int_{0}^{1} t e^{t} \; dt - \int_{0}^{1} t^{2} e^{t} \; dt \\ &= 1 - (e - 2) = 3 - e \end{align*}$$
연습문제9. 주어진 매개변수 곡선들과 $t$의 범위에 대해 곡선의 길이를 구하는 공식을 세워라. (계산은 하지 않아도 됨)
(a). $x = t - t^{2}, y = \frac{4}{3} t^{\frac{3}{2}}, 1 \le t \le 2$
(b). $x = 1 + e^{t}, y = t^{2}, -3 \le t \le 3$
(c). $x =t + \cos(t), y = t - \sin(t), 0 \le t \le 2\pi$
(d). $x = \ln (t), y = \sqrt{t + 1}, 1 \le t \le 5$
(a). $x = t - t^{2}, y = \frac{4}{3} t^{\frac{3}{2}}, 1 \le t \le 2$
$$\begin{align*} L &= \int_{1}^{2} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{1}^{2} \sqrt{ (1 - 2t)^{2} + (2 t^{\frac{1}{2}})^{2} } \; dt \\ &= \int_{1}^{2} \sqrt{ 4t^{2} - 4t + 5 } \; dt \end{align*}$$
(b). $x = 1 + e^{t}, y = t^{2}, -3 \le t \le 3$
$$\begin{align*} L &= \int_{-3}^{3} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{-3}^{-3} \sqrt{ (e^{t})^{2} + (2t)^{2} } \; dt \\ &= \int_{-3}^{3} \sqrt{ e^{2t} + 4t^{2} } \; dt \end{align*}$$
(c). $x =t + \cos(t), y = t - \sin(t), 0 \le t \le 2\pi$
$$\begin{align*} L &= \int_{0}^{2\pi} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{2\pi} \sqrt{ (1 - \sin(t))^{2} + (1 - \cos(t))^{2} } \; dt \\ &= \int_{0}^{2\pi} \sqrt{ (1 - 2\sin(t) + \sin^{2}(t)) + (1 - 2\cos(t) + \cos^{2}(t)) } \; dt \\ &= \int_{0}^{2\pi} \sqrt{2 - 2\sin(t) - 2\cos(t)} \; dt \end{align*}$$
(d). $x = \ln (t), y = \sqrt{t + 1}, 1 \le t \le 5$
$$\begin{align*} L &= \int_{1}^{5} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{1}^{5} \sqrt{ (\frac{1}{t})^{2} + (\frac{1}{2\sqrt{t + 1}})^{2} } \; dt \\ &= \int_{1}^{5} \sqrt{ \frac{1}{t^{2}} + \frac{1}{4(t + 1)} } \; dt \end{align*}$$
연습문제10. 주어진 매개변수 곡선들과 $t$의 범위에 대해 곡선의 길이를 구하라.
(a). $x = 1 + 3t^{2}, y = 4 + 2t^{3}, 0 \le t \le 1$
(b). $x = e^{t} + e^{-t}, y = 5 - 2t, 0 \le t \le 3$
(c). $x = \frac{t}{1 + t}, y = \ln (1 + t), 0 \le t \le 2$
(d). $x = 3 \cos(t) - \cos(3t), y = 3 \sin(t) - \sin(3t), 0 \le t \le \pi$
(a). $x = 1 + 3t^{2}, y = 4 + 2t^{3}, 0 \le t \le 1$
$$\begin{align*} L &= \int_{0}^{1} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} \sqrt{ (6t)^{2} + (6t^{2})^{2} } \; dt \\ &= \int_{0}^{1} \sqrt{ 36t^{2} + 36t^{4} } \; dt \\ &= \int_{0}^{1} 6t \sqrt{1 + t^{2}} \; dt \end{align*}$$
위 식에서 $t = \tan(\theta)$라고 하면 $dt = \sec^{2}(\theta) d\theta$이고 적분구간은 $[0, 1] \xrightarrow{\theta = \arctan(t)} [\arctan(0), \arctan(1)] = [0, \frac{\pi}{4}]$이다.
$$\begin{align*} L &= \int_{0}^{1} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} \sqrt{ (6t)^{2} + (6t^{2})^{2} } \; dt \\ &= \int_{0}^{1} \sqrt{ 36t^{2} + 36t^{4} } \; dt \\ &= \int_{0}^{1} 6t \sqrt{1 + t^{2}} \; dt \\ &= 6 \int_{0}^{\frac{\pi}{4}} \tan(\theta) \sqrt{ 1 + \tan^{2} (\theta) } \sec^{2} (\theta) \; d\theta \\ &= 6 \int_{0}^{\frac{\pi}{4}} \tan (\theta) \sec (\theta) \sec^{2} (\theta) \; d\theta \end{align*} - (1)$$
위 식에서 $\sec(\theta) = u$라고 하면 $\sec(\theta) \tan(\theta) d\theta = du \rightarrow d\theta = \frac{1}{\sec(\theta) \tan(\theta)} du$이고 적분구간은 $[0, \frac{\pi}{4}] \xrightarrow{u = \sec(\theta)} [\sec(0), \sec(\frac{\pi}{4})] = [1, \sqrt{2}]$이다. 이제 (1) 식에서 이어서 쓰면 다음과 같다.
$$\begin{align*} L &= \int_{0}^{1} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} 6t \sqrt{1 + t^{2}} \; dt \\ &= 6 \int_{0}^{\frac{\pi}{4}} \tan (\theta) \sec (\theta) \sec^{2} (\theta) \; d\theta \\ &= 6 \int_{1}^{\sqrt{2}} \tan(\theta) \sec(\theta) u^{2} \frac{1}{\tan(\theta) \sec(\theta)} \; du \\ &= 6 \int_{1}^{\sqrt{2}} u^{2} \; du \\ &= 6 \left[ \frac{1}{3}u^{3} \right]_{1}^{\sqrt{2}} = 2(2\sqrt{2} - 1) \end{align*}$$
(b). $x = e^{t} + e^{-t}, y = 5 - 2t, 0 \le t \le 3$
$$\begin{align*} L &= \int_{0}^{3} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{3} \sqrt{ (e^{t} - e^{-t})^{2} + (-2)^{2} } \; dt \\ &= \int_{0}^{3} \sqrt{ e^{2t} - 2 + e^{-2t} + 4 } \; dt \\ &= \int_{0}^{3} \sqrt{e^{2t} + 2 + e^{-2t}} \; dt \\ &= \int_{0}^{3} \sqrt{ (e^{t} + e^{-t})^{2} } \; dt \\ &= \int_{0}^{3} (e^{t} + e^{-t}) \; dt \\ &= \left[ e^{t} - e^{-t} \right]_{0}^{3} \\ &= e^{3} - e^{-3} \end{align*}$$
(c). $x = \frac{t}{1 + t}, y = \ln (1 + t), 0 \le t \le 2$
$$\begin{align*} L &= \int_{0}^{2} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{2} \sqrt{ (\frac{1}{(1 + t)^{2}})^{2} + (\frac{1}{1 + t})^{2} } \; dt \\ &= \int_{0}^{2} \sqrt{ \frac{1}{(1 + t)^{4}} (1 + (1 + t)^{2}) } \; dt \\ &= \int_{0}^{2} \frac{1}{(1 + t)^{2}} \sqrt{1 + (1 + t)^{2}} \; dt \end{align*} - (1)$$
식 (1)에서 $1 + t = u$라고 하면 $dt = du$이고 적분구간은 $[0, 2] \xrightarrow{u = t + 1} [1, 3]$이다. 이제 (1) 식에서 이어서 쓰면 다음과 같다.
$$\begin{align*} L &= \int_{0}^{2} \frac{1}{(1 + t)^{2}} \sqrt{1 + (1 + t)^{2}} \; dt \\ &= \int_{1}^{3} \frac{1}{u^{2}} \sqrt{1 + u^{2}} \; du \\ &= \int_{1}^{3} \frac{\sqrt{1 + u^{2}}}{u^{2}} \end{align*} - (2)$$
식 (2)에서 $f(u) = \sqrt{1 + u^{2}}$ 그리고 $g^{'} (u) = \frac{1}{u^{2}}$라고 하자. 따라서 $f^{'}(u) = \frac{u}{\sqrt{1 + u^{2}}}$ 이고 $g(u) = -\frac{1}{u}$이다. 부분적분을 통해 식 (2)는 다음과 같이 적분할 수 있다.
$$\begin{align*} L &= \int_{1}^{3} \frac{\sqrt{1 + u^{2}}}{u^{2}} \; du \\ &= \int_{1}^{3} f(u) g^{'}(u) \; du \\ &= \left[ f(u) g(u) \right]_{1}^{3} - \int_{1}^{3} f^{'}(u) g(u) \; du \\ &= \left[ -\frac{\sqrt{1 + u^{2}}}{u} \right]_{1}^{3} - \int_{1}^{3} \frac{u}{\sqrt{1 + u^{2}}} \cdot \left( -\frac{1}{u} \right) \; dt \\ &= \left( \sqrt{2} - \frac{1}{3}\sqrt{10} \right) + \int_{1}^{3} \frac{1}{\sqrt{1 + u^{2}}} \; du \end{align*} - (3)$$
식 (3)의 두 개의 적분항 중 두번째 항은 $u = \tan(\theta)$라고 하면 $du = \sec^{2} (\theta) d\theta$이고 적분구간은 $[1, 3] \xrightarrow{\theta = \arctan (u)} [\arctan(1), \arctan(3)] = [\frac{\pi}{4}, \alpha]$이다. 여기서, $\alpha = \arctan(3)$이다. 따라서 적분항은 다음과 같이 적분할 수 있다.
$$\begin{align*} \int_{1}^{3} \frac{1}{\sqrt{1 + u^{2}}} \; du &= \int_{\frac{\pi}{4}}^{\alpha} \frac{1}{\sqrt{1 + \tan^{2} (\theta)}} \cdot \sec^{2} (\theta) \; d\theta \\ &= \int_{\frac{\pi}{4}}^{\alpha} \frac{1}{\sec(\theta)} \cdot \sec^{2} (\theta) \; d\theta \\ &= \int_{\frac{\pi}{4}}^{\alpha} \sec(\theta) \; d\theta \\ &= \left[ \ln | \sec(\theta) + \tan(\theta) | \right]_{\frac{\pi}{4}}^{\alpha} \end{align*} - (4)$$
식 (4)에서 $u = \tan(\theta)$임을 고려하면 $\sec(\theta) = \sqrt{u^{2} + 1}$과 동일하므로 다시 $u$에 대한 적분으로 다음과 같이 표현할 수 있다.
$$\begin{align*} \int_{1}^{3} \frac{1}{\sqrt{1 + u^{2}}} \; du &= \left[ \ln | \sec(\theta) + \tan(\theta) | \right]_{\frac{\pi}{4}}^{\alpha} \\ &= \left[ \ln | \sqrt{u^{2} + 1} + u | \right]_{1}^{3} = \ln (\sqrt{10} + 3) - \ln (\sqrt{2} + 1) \end{align*} - (5)$$
이제 식 (5)의 결과를 식 3에 더하면 최종 곡선의 길이를 얻을 수 있다.
$$\begin{align*} L &= \left( \sqrt{2} - \frac{1}{3}\sqrt{10} \right) + \int_{1}^{3} \frac{1}{\sqrt{1 + u^{2}}} \; du = \left( \sqrt{2} - \frac{1}{3} \sqrt{10} \right) + \left( \ln (\sqrt{10} + 3) - \ln (\sqrt{2} + 1) \right) \end{align*} $$
(d). $x = 3 \cos(t) - \cos(3t), y = 3 \sin(t) - \sin(3t), 0 \le t \le \pi$
$$\begin{align*} L &= \int_{0}^{\pi} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{\pi} \sqrt{ (-3\sin(t) + 3\sin(3t))^{2} + (3\cos(t) - 3\cos(t))^{2} } \; dt \\ &= \int_{0}^{\pi} \sqrt{ (9\sin^{2} (t) - 18\sin(t)\sin(3t) + 9\sin^{2} (3t)) + (9\cos^{2} (t) - 18\cos(t)\cos(3t) + 9\cos^{2}(3t)) } \; dt \\ &= \int_{0}^{\pi} \sqrt{9 (\sin^{2} (t) + \cos^{2} (t)) + 9 (\sin^{2} (3t) + \cos^{2} (3t)) - 18 (\sin(t)\sin(3t) + \cos(t)\cos(3t))} \; dt \\ &= \int_{0}^{\pi} \sqrt{ 18 - 18\cos(2t) } \; dt \\ &= \int_{0}^{\pi} \sqrt{18} \sqrt{1 - (1 - 2\sin^{2} (t))} \; dt \\ &= \int_{0}^{\pi} \sqrt{36} \sqrt{\sin^{2} (t)} \; dt \\ &= 6 \int_{0}^{\pi} \sin(t) \; dt \\ &= 6 \left[ -\cos(t) \right]_{0}^{\pi} = 6 \cdot 2 = 12 \end{align*}$$
연습문제11. 매개변수 곡선 $x = 3t - t^{3}, y = 3t^{2}$의 루프의 길이를 구하여라.
문제를 해결하기 위해 주어진 곡선의 넓이를 그린다. (편의를 위해 WolframAlpha 이용하였습니다.)
STEP1. 주어진 매개변수 함수 그리기
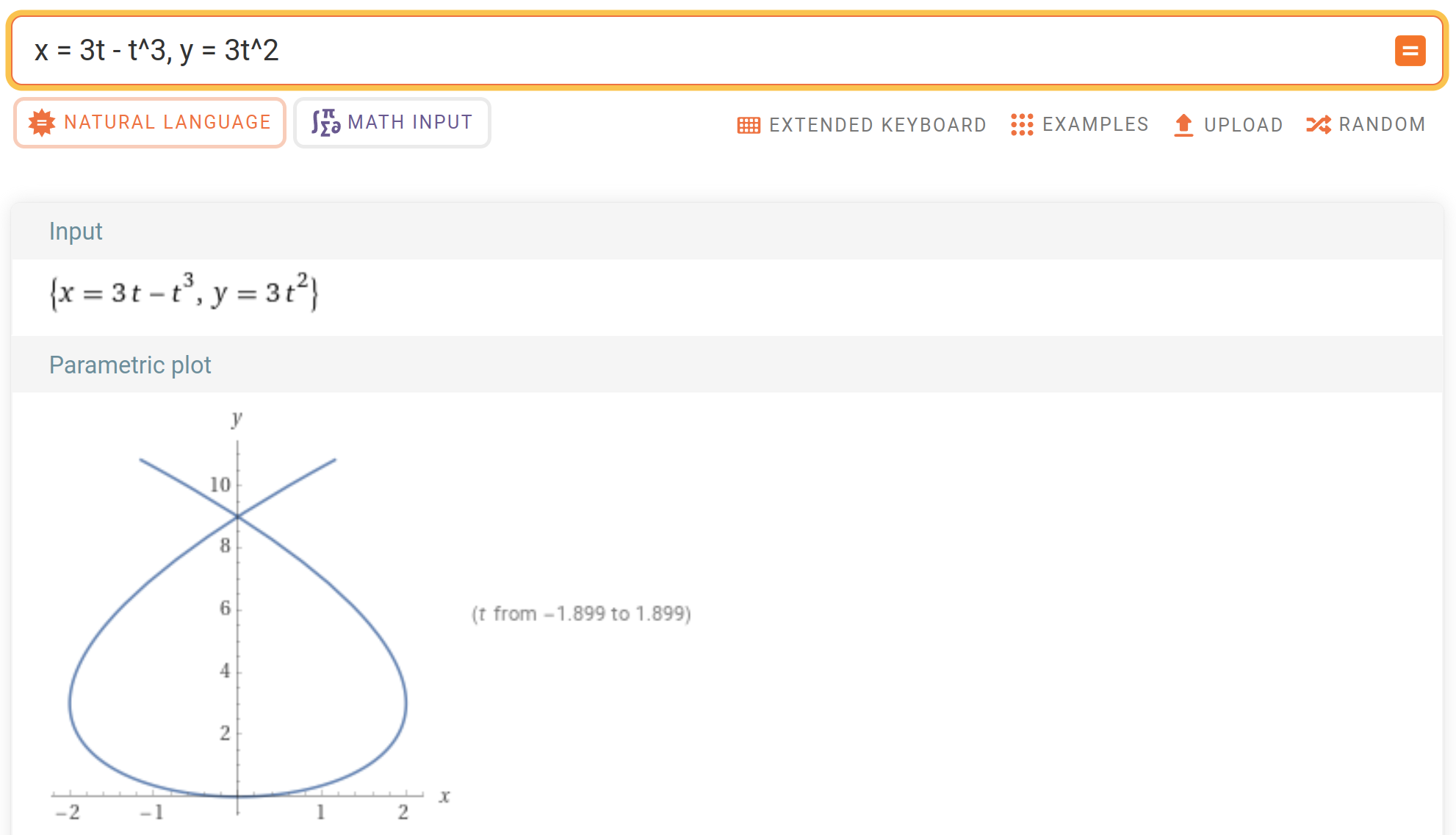
위 그림에서 루프가 생긴 지점을 확인할 수 있다. 즉, $x(t) = 0$이 되는 지점을 의미한다.
STEP2. 해당 매개변수 곡선에 대한 길이 공식 적용
이때, $t$의 범위는 $x(t) = 0$이 되는 지점의 시작점과 끝점이다. 따라서, $x(t) = 3t - t^{3} = t(\sqrt{3} - t)(\sqrt{3} + t) = 0$이라고 하면 $t = 0$ 그리고 $t = \pm \sqrt{3}$에서 $x(t) = 0$이다. 따라서, 전체 루프는 $t = -\sqrt{3}$부터 $t = \sqrt{3}$에서 라고 할 수 있다. 이제 곡선의 길이를 다음과 같이 구할 수 있다.
$$\begin{align*} L &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{ (3 - 3t^{2})^{2} + ( 6t )^{2} } \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{9 - 18t^{2} + 9t^{4} + 36t^{2}} \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{9 + 18t^{2} + 9t^{4}} \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{(3 + 3t^{2})^{2}} \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} (3 + 3t^{2}) \; dt \\ &= 2 \int_{0}^{\sqrt{3}} (3 + 3t^{2}) \; dt \\ &= 2 \left[ 3t + t^{3} \right]_{0}^{\sqrt{3}} = 12\sqrt{3} \end{align*}$$
연습문제12. 주어진 매개변수 곡선들과 $t$의 범위에 대해서 $x$축을 중심으로 회전했을 때 얻을 수 있는 회전체의 겉넓이에 대한 공식을 세워라. (계산은 하지 않아도 됨)
(a). $x = 1 + te^{t}, y = (t^{2} + 1) e^{t}, 0 \le t \le 1$
(b). $x = \sin^{2} (t), y = \sin(3t), 0 \le t \le \frac{\pi}{3}$
(a). $x = 1 + te^{t}, y = (t^{2} + 1) e^{t}, 0 \le t \le 1$
$$\begin{align*} S &= \int_{0}^{1} 2\pi y \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} 2 \pi (t^{2} + 1) e^{t} \sqrt{ (e^{t} + te^{t})^{2} + (2t e^{t} + (t^{2} + 1) e^{t})^{2} } \; dt \\ &= \int_{0}^{1} 2 \pi (t^{2} + 1) e^{t} \sqrt{ \left[ (1 + t) e^{t} \right]^{2} + \left[ (t + 1)^{2}e^{t} \right]^{2} } \; dt \end{align*}$$
(b). $x = \sin^{2} (t), y = \sin(3t), 0 \le t \le \frac{\pi}{3}$
$$\begin{align*} S &= \int_{0}^{\frac{\pi}{3}} 2\pi y \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{\frac{\pi}{3}} 2 \pi \sin (3t) \sqrt{ (2\sin(t)\cos(t))^{2} + (3\cos(3t))^{2} } \; dt \\ &= \int_{0}^{\frac{\pi}{3}} 2 \pi \sin(3t) \sqrt{ \sin^{2} (2t) + 9\cos^{2} (3t) } \; dt \end{align*}$$
연습문제13. 주어진 매개변수 곡선들과 $t$의 범위에 대해서 $x$축을 중심으로 회전했을 때 얻을 수 있는 회전체의 겉넓이를 구하여라.
(a). $x = 3t - t^{3}, y = 3t^{2}, 0 \le t \le 1$
(b). $x = a\cos^{3} (\theta), y = a \sin^{3} (\theta), 0 \le \theta \le \frac{\pi}{2}$
(a). $x = 3t - t^{3}, y = 3t^{2}, 0 \le t \le 1$
$$\begin{align*} S &= \int_{0}^{1} 2\pi y \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} 2 \pi 3t^{2} \sqrt{ (3 - 3t^{2})^{2} + (6t)^{2} } \; dt \\ &= \int_{0}^{1} 2 \pi 3t^{2} \sqrt{ (9 - 18t^{2} + 9t^{4}) + 36t^{2} } \; dt \\ &= \int_{0}^{1} 2 \pi 3t^{2} \sqrt{9t^{4} + 18t^{2} + 9} \; dt \\ &= \int_{0}^{1} 2\pi 3t^{2} \sqrt{(3t^{2} + 3)^{2}} \; dt \\ &= \int_{0}^{1} 2\pi 3t^{2} (3t^{2} + 3) \; dt \\ &= \int_{0}^{1} 2\pi 3t^{2} (3t^{2} + 3) \; dt \\ &= 2\pi \int_{0}^{1} (9t^{4} + 9t^{2}) \; dt \\ &= 18\pi \left[ \frac{1}{5} t^{5} + \frac{1}{3} t^{3} \right]_{0}^{1} = 18\pi \left( \frac{1}{5} + \frac{1}{3} \right) = \frac{144\pi}{15} \end{align*}$$
(b). $x = a\cos^{3} (\theta), y = a \sin^{3} (\theta), 0 \le \theta \le \frac{\pi}{2}$
$$\begin{align*} S &= \int_{0}^{\frac{\pi}{2}} 2\pi y \sqrt{\left( \frac{dx}{dt\theta} \right)^{2} + \left( \frac{dy}{d\theta} \right)^{2}} \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2 \pi a \sin^{3} (\theta) \sqrt{ (-3a\sin(\theta)\cos^{2}(\theta))^{2} + (3a\sin^{2}(\theta)\cos(\theta))^{2} } \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2 \pi a\sin^{3} (\theta) \sqrt{ 9a^{2}\sin^{2}(\theta)\cos^{4}(\theta) + 9a^{2}\sin^{4}(\theta)\cos^{2}(\theta) } \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2 \pi a\sin^{3} (\theta) \sqrt{9a^{2}\sin^{2}(\theta)\cos^{2}(\theta) (\sin^{2} (\theta) + \cos^{2} (\theta))} \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2\pi 3a\sin^{3}(\theta) \sqrt{(3a\sin(\theta)\cos(\theta))^{2}} \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2\pi (3a\sin^{3} (\theta)) (3a\sin(\theta)\cos(\theta)) \; d\theta \\ &= 6a^{2}\pi \int_{0}^{\frac{\pi}{2}} \sin^{4} (\theta)\cos(\theta) \; d\theta \end{align*} - (1)$$
식 (1)에서 $\sin(\theta) = u$라고 하면 $\cos(\theta) d\theta = du \rightarrow d\theta = \frac{1}{\cos(\theta)} du$이고 적분구간은 $[0, \frac{\pi}{2}] \xrightarrow{u = \sin(\theta)} [0, 1]$이다. 이제 (1) 식에서 이어서 쓰면 다음과 같다.
$$\begin{align*} S &= 6a^{2}\pi \int_{0}^{\frac{\pi}{2}} \sin^{4} (\theta)\cos(\theta) \; d\theta \\ &= 6a^{2} \pi \int_{0}^{1} u^{4} \cos(\theta) \frac{1}{\cos(\theta)} \; du \\ &= 6a^{2}\pi \int_{0}^{1} u^{4} \; du = 6a^{2} \pi \left[ \frac{1}{5} u^{5} \right]_{0}^{1} = \frac{6}{5}a^{2}\pi \end{align*}$$
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 극좌표계 곡선 (0) | 2022.04.09 |
|---|---|
| 미적분학 - 극좌표계 (0) | 2022.04.08 |
| 미적분학 - 매개변수 함수 (0) | 2022.04.02 |
| 미적분학 - 일 (1) | 2022.03.30 |
| 미적분학 - 회전체의 겉넓이 (2) | 2022.03.29 |
안녕하세요. 지난 포스팅의 미적분학 - 매개변수 함수에서는 매개변수가 포함된 간단한 함수들의 정의와 유명한 사이클로이드(cycloid) 함수까지 매개변수로 표현해보았습니다. 오늘은 매개변수 함수에서 미적분학을 어떻게 적용할 수 있는 지 알아보도록 하겠습니다.
미적분학 - 매개변수 함수
안녕하세요. 지난 포스팅의 미적분학 - 일에서는 적분을 물리학에 응용하는 방법에 대해서 알아보았습니다. 지금까지 저희는 극한, 미분, 적분을 통해 기본적인 미적분학의 지식은 갖추었습니
everyday-image-processing.tistory.com
1. 기울기(Tangent)
매개변수 함수에서는 x=f(t),y=g(t)로 표현될 수 있다고 하였습니다. 그리고 만약, 매개변수 t를 소거할 수 있다면 y=F(x)의 꼴로 나타낼 수 있겠죠.
y=F(x)⇒g(t)=F(f(t))
따라서, g,f,F가 모두 미분가능하다면 미적분학 - 연쇄 법칙에서 보았던 연쇄 법칙을 이용해서 아래와 같이 미분할 수 있습니다.
g′(t)=F′(f(t))f′(t)=F′(x)f′(t)
여기서 f′(t)≠0이라면 F′(x)=g′(t)f′(t)를 통해 매개변수 함수 꼴의 미분을 구할 수 있습니다. 만약, 라이브니츠 표기법(Leibniz Notation)을 이용해서 표현하면 아래와 같습니다.
dydx=dy/dtdx/dt
이제, 고계도미분까지 해볼까요? 이 역시 정의를 이용하면 쉽게 할 수 있습니다.
d2ydx2=ddx(dydx)=ddt(dydx)dxdt
예제1. θ=π3에서 사이클로이드 곡선 x=r(θ−sin(θ)),y=r(1−cos(θ))의 기울기를 구하여라.
dydx=dy/dθdx/dθ=sin(θ)1−cos(θ)
따라서, θ=π3에서 사이클로이드 곡선의 기울기는 dydxθ=π3=sin(π3)1−cos(π3)=√3이다.
2. 영역의 넓이(Area)
다음으로 넓이입니다. 저희가 미적분학 - 두 곡선 사이의 넓이에서 보았던 식에 의하면 y=F(x)가 주어졌을 때, 닫힌 구간 [a,b]로 둘러쌓인 영역의 넓이는 A=∫baF(x)dx로 구할 수 있었습니다. 하지만, x=f(t),y=g(t)와 같이 매개변수로 주어져있을 때는 어떻게 계산할 수 있을까요? 전혀 어렵지 않으니 천천히 보시길 바랍니다. 일단, α≤t≤β에서 정의되었다고 가정하겠습니다. 그리고 F(x)=y=g(t)이고 x=f(t)⇒dx=f′(t)dt입니다. 따라서, 아래와 같이 계산하면 원하는 영역의 넓이를 구할 수 있습니다.
A=∫baydx=∫βαg(t)f′(t)dt
예제2. 사이클로이드 곡선 x=r(θ−sin(θ)),y=r(1−cos(θ))의 한 주기에 해당하는 넓이를 구하여라.
사이클로이드 곡선의 한 주기는 0≤θ≤2π이고 dx=r(1−cos(θ))이기 때문에 아래와 같이 적분가능하다.
A=∫2π0r(1−cos(θ))⋅r(1−cos(θ))dθ=r2∫2π0(1−cos(θ))2dθ=r2∫2π0(1−2cos(θ)+cos2(θ))dθ=r2∫2π0(1−2cos(θ)+(1+cos(2θ)2))dθ=r2[32θ−2sin(θ)+14sin(2θ)]2π0=r232⋅2π=3r2π
3. 곡선의 길이 (Arc Length)
함수 y=F(x)와구간a \le x \le b로둘러쌓인곡선C$의 길이를 구하는 방법은 미적분학 - 곡선의 길이에서 알아보았습니다. 그 결과 아래의 식을 통해서 구할 수 있었죠.
L=∫ba√1+(dydx)2dx
이제부터는 곡선 C가 매개변수 함수의 꼴로 x=f(t),y=g(t)로 주어졌다고 가정하겠습니다. 그리고 t의 범위는 α≤t≤β입니다.
L=∫ba√1+(dy/dtdx/dt)2dxdtdt=∫βα√(dxdt)2+(dydt)2dt
예제1. 0≤t≤2π일 때, x=cos(t),y=sin(t)로 이루어지는 곡선의 자취의 길이를 구하여라.
dxdt=−sin(t),dydt=cos(t)이기 때문에 아래와 같이 적분 가능하다.
L=∫2π0√sin2(t)+cos2(t)dt=∫2π01dt=[t]2π0=2π
예제2. 사이클로이드 곡선 x=r(θ−sin(θ)),y=r(1−cos(θ))의 한 주기에 해당하는 곡선의 길이를 구하여라.
dxdθ=r(1−cos(θ)),dydθ=rsin(θ)이기 때문에 아래와 같이 적분 가능하다.
L=∫2π0√[r(1−cos(θ))]2+[rsin(θ)]2dt=∫2π0√r2(1−cos(θ))2+r2sin2(θ)dt=r∫2π0√1−2cos(θ)+cos2(θ)+sin2(θ)dt=r∫2π0√2(1−cos(θ))dt=r∫2π0√4sin2(θ2)dt=r∫2π02sin(θ2)dt=2r[−2cos(θ2)]2π0=2r(2+2)=8r
4. 곡면의 겉넓이 (Surface Area)
곡면의 겉넓이 역시 쉽게 공식을 바꾸어서 해결할 수 있습니다.
S=∫βα2πy√(dxdt)2+(dydt)2dt
연습문제1. 주어진 매개변수 곡선의 기울기 dydx를 구하여라.
(a). x=tsin(t),y=t2+t
(b). x=1t,y=√te−t
(a). x=tsin(t),y=t2+t
매개변수 곡선의 기울기는 dydx=dy/dtdx/dt이므로 먼저 dydt 그리고 dxdt를 구한다.
{dydt=2t+1dxdt=sin(t)+tcos(t)
따라서, 주어진 곡선의 기울기는 다음과 같이 구할 수 있다.
dydx=dy/dtdx/dt=2t+1sin(t)+tcos(t)
(b). x=1t,y=√te−t
매개변수 곡선의 기울기는 dydx=dy/dtdx/dt이므로 먼저 dydt 그리고 dxdt를 구한다.
{dydt=1√te−t−√te−t=(12√t−√t)e−tdxdt=−1t2
따라서, 주어진 곡선의 기울기는 다음과 같이 구할 수 있다.
dydx=dy/dtdx/dt=(12√t−√t)e−t−1t2=t32(t−12)e−t
연습문제2. 매개변수 곡선과 점이 주어졌을 때 해당 점에서 접선의 방정식을 구하여라.
(a). x=t4+1,y=t3+t,t=−1
(b). x=t−1t,y=1+t2,t=1
(c). x=e√t,y=t−lnt2,t=1
(d). x=cos(θ)+2sin(2θ),y=sin(θ)+cos(2θ),θ=0
(a). x=t4+1,y=t3+t,t=−1
먼저 주어진 매개변수 곡선에 대해 점 t=−1에서의 접선의 기울기를 구한다.
dydx=dy/dtdx/dt=3t2+14t3
위 식에 t=−1을 대입하면 접선의 기울기가 -1임을 알 수 있다. 이때, t=−1을 두 매개변수 방정식 x(t)와 y(t)에 대입하면 해당 시점에서 접선이 지나는 점이 (2,−2)임을 알 수 있다. 따라서, 해당 매개변수 곡선 (x(t),y(t))가 시점 t=−1에서의 접선의 방정식은 다음과 같다.
y=−(x−2)−2=−x
(b). x=t−1t,y=1+t2,t=1
먼저 주어진 매개변수 곡선에 대해 점 t=1에서의 접선의 기울기를 구한다.
dydx=dy/dtdx/dt=2t1+1t2
위 식에 t=1을 대입하면 접선의 기울기가 1임을 알 수 있다. 이때, t=1을 두 매개변수 방정식 x(t)와 y(t)에 대입하면 해당 시점에서 접선이 지나는 점이 (0,2)임을 알 수 있다. 따라서, 해당 매개변수 곡선 (x(t),y(t))가 시점 t=1에서의 접선의 방정식은 다음과 같다.
y=(x−0)+2=x+2
(c). x=e√t,y=t−lnt2,t=1
먼저 주어진 매개변수 곡선에 대해 점 t=1에서의 접선의 기울기를 구한다.
dydx=dy/dtdx/dt=1−2t12√te√t
위 식에 t=1을 대입하면 접선의 기울기가 −2e임을 알 수 있다. 이때, t=1을 두 매개변수 방정식 x(t)와 y(t)에 대입하면 해당 시점에서 접선이 지나는 점이 (e,1)임을 알 수 있다. 따라서, 해당 매개변수 곡선 (x(t),y(t))가 시점 t=1에서의 접선의 방정식은 다음과 같다.
y=−2e(x−e)+1=−2ex+3
(d). x=cos(θ)+2sin(2θ),y=sin(θ)+cos(2θ),θ=0
먼저 주어진 매개변수 곡선에 대해 점 θ=0에서의 접선의 기울기를 구한다.
dydx=dy/dθdx/dθ=cos(θ)−2sin(2θ)−sin(θ)+2cos(2θ)
위 식에 θ=0을 대입하면 접선의 기울기가 12임을 알 수 있다. 이때, θ=1을 두 매개변수 방정식 x(θ)와 y(θ)에 대입하면 해당 시점에서 접선이 지나는 점이 (1,1)임을 알 수 있다. 따라서, 해당 매개변수 곡선 (x(θ),y(θ))가 시점 θ=1에서의 접선의 방정식은 다음과 같다.
y=12(x−1)+1=12x+12
연습문제3. 매개변수 곡선과 점이 주어졌을 때 해당 점에서 접선의 방정식을 구하여라.
(a). x=1+ln(t),y=t2+2,(1,3)
(b). x=tan(θ),y=sec(θ),(1,√2)
(a). x=1+ln(t),y=t2+2,(1,3)
먼저 주어진 매개변수 곡선에 대해 점 (1,3)에서의 접선의 기울기를 구한다.
dydx=dy/dtdx/dt=2t1t=2t2=2(y−2)
위 식에 y=3을 대입하면 접선의 기울기가 2임을 알 수 있다. 따라서, 해당 매개변수 곡선 (x(t),y(t))가 점 (1,3)에서의 접선의 방정식은 다음과 같다.
y=2(x−1)+3=2x+1
(b). x=tan(θ),y=sec(θ),(1,√2)
먼저 주어진 매개변수 곡선에 대해 점 θ=0에서의 접선의 기울기를 구한다.
dydx=dy/dθdx/dθ=sec(θ)tan(θ)sec2(θ)=tan(θ)sec(θ)=xy
위 식에 (x,y)=(1,√2)을 대입하면 접선의 기울기가 1√2임을 알 수 있다. 따라서, 해당 매개변수 곡선 (x(t),y(t))가 점 (1,√2)에서의 접선의 방정식은 다음과 같다.
y=1√2(x−1)+√2
연습문제4. 주어진 매개변수 곡선의 2차 미분 d2ydx2를 구하여라.
(a). x=4+t2,y=t2+t3
(b). x=t3−12t,y=t2−1
(c). x=t−et,y=t+e−t
(d). x=t+ln(t),y=t−ln(t)
(e). x=2sin(t),y=3cos(t),0<t<2π
(f). x=cos(2t),y=cos(t),0<t<π
(a). x=4+t2,y=t2+t3
매개변수 곡선의 2차 미분은 d2ydx2=d/dtdx/dt(dy/dtdx/dt)이므로 다음과 같이 구할 수 있다.
d2ydx2=d/dtdx/dt(dy/dtdx/dt)=d/dtdx/dt(2t+3t22t)=d/dtdx/dt(1+3t2)=3/22t=34t
(b). x=t3−12t,y=t2−1
매개변수 곡선의 2차 미분은 d2ydx2=d/dtdx/dt(dy/dtdx/dt)이므로 다음과 같이 구할 수 있다.
d2ydx2=d/dtdx/dt(dy/dtdx/dt)=d/dtdx/dt(2t3t2−12)=2(3t2−12)−2t⋅6t(3t2−12)2⋅13t2−12=6t2−24−12t2(3t2−12)3=−6(t2+4)27(t2−4)3=−2(t2+4)9(t2−4)3
(c). x=t−et,y=t+e−t
매개변수 곡선의 2차 미분은 d2ydx2=d/dtdx/dt(dy/dtdx/dt)이므로 다음과 같이 구할 수 있다.
d2ydx2=d/dtdx/dt(dy/dtdx/dt)=d/dtdx/dt(1−e−t1−et)=e−t(1−et)+et(1−e−t)(1−et)2⋅11−et=e−t−1+et−1(1−et)3=e−t+et−2(1−et)3
(d). x=t+ln(t),y=t−ln(t)
매개변수 곡선의 2차 미분은 d2ydx2=d/dtdx/dt(dy/dtdx/dt)이므로 다음과 같이 구할 수 있다.
d2ydx2=d/dtdx/dt(dy/dtdx/dt)=d/dtdx/dt(1+1t1−1t)=d/dtdx/dt(t+1t−1)=(t−1)−(t+1)(t−1)2⋅tt−1=−2t(t−1)3
(e). x=2sin(t),y=3cos(t),0<t<2π
매개변수 곡선의 2차 미분은 d2ydx2=d/dtdx/dt(dy/dtdx/dt)이므로 다음과 같이 구할 수 있다.
d2ydx2=d/dtdx/dt(dy/dtdx/dt)=d/dtdx/dt(−3sin(t)2cos(t))=−3cos(t)⋅2cos(t)+(−3sin(t))⋅(−2sin(t))4cos2(t)⋅12cos(t)=−6(sin2(t)+cos2(t))4cos2(t)⋅12cos(t)=−64cos2(t)⋅12cos(t)=−34cos3(t)
(f). x=cos(2t),y=cos(t),0<t<π
매개변수 곡선의 2차 미분은 d2ydx2=d/dtdx/dt(dy/dtdx/dt)이므로 다음과 같이 구할 수 있다.
d2ydx2=d/dtdx/dt(dy/dtdx/dt)=d/dtdx/dt(−sin(t)−2sin(2t))=d/dtdx/dt(sin(t)4sin(t)cos(t))=d/dtdx/dt(14cos(t))=−sin(t)4cos2(t)⋅1−2sin(2t)=sin(t)4cos2(t)⋅14sin(t)cos(t)=116cos3(t)
연습문제5. 주어진 매개변수 곡선에서 접선이 수직 또는 수평인 점을 찾아라.
(a). x=10−t2,y=t3−12t
(b). x=2t3+3t2−12t,y=2t3+3t2+1
(a). x=10−t2,y=t3−12t
매개변수 곡선의 기울기 dydx=dy/dtdx/dt를 먼저 구한다.
dydx=dy/dtdx/dt=3t2−12−2t=3(t−2)(t+2)−2t
1). 접선이 수평인 경우
위 식에서 3(t−2)(t+2)−2t=0이라고 할 때 t=2 그리고 t=−2일 때 접선이 0이므로 두 점 (6,−16) 그리고 (6,16)에서 수평이다.
2). 접선이 수직인 경우
위 식에서 t=0일 때 기울기가 무한대로 발산하므로 점 (10,0)에서 수직이다.
(b). x=2t3+3t2−12t,y=2t3+3t2+1
매개변수 곡선의 기울기 dydx=dy/dtdx/dt를 먼저 구한다.
dydx=dy/dtdx/dt=6t2+6t6t2+6t−12=t(t+1)(t+2)(t−1)
1). 접선이 수평인 경우
위 식에서 t(t+1)(t+2)(t−1)=0이라고 할 때 t=0 그리고 t=−1일 때 접선이 0이므로 두 점 (0,1) 그리고 (13,2)에서 수평이다.
2). 접선이 수직인 경우
위 식에서 t=−2 그리고 t=1일 때 기울기가 무한대로 발산하므로 점 (20,−3) 그리고 (−7,6)에서 수직이다.
연습문제6. 타원의 매개변수 방정식 x=acos(θ),y=bsin(θ),0≤θ≤2π를 이용하여 내부 넓이를 구하여라.
타원의 특징 중 하나는 원점을 중심으로 가지는 타원의 특징 중 하나는 각 사분면의 해당하는 넓이가 동일하다는 것이다. 이를 이용하여 0≤θ≤2π까지에 해당되는 넓이를 구하는 것이 아닌 제 1사분면인 0≤θ≤π2에 해당하는 타원의 넓이를 구한 뒤 4를 곱해준다.
먼저 θ=0이면 x=a,y=0이다. 그리고 θ=π2이면 x=0,y=a이다. 따라서, 타원 내부의 전체 넓이는 다음과 같이 구할 수 있다. 여기서 주의해야할 점은 x에 대해 적분을 수행 시 x=0→x=a는 θ=π2→θ=0이라는 점이다.
A=4∫0π2ydx=4∫0π2bsin(θ)(−asin(θ))dθ=4ab∫π20sin2(θ)dθ=4ab∫π201−cos(2θ)2dθ=2ab∫π20(1−2cos(2θ))dθ=2ab[θ−sin(2θ)]π20=2ab(π2)=abπ
연습문제7. 매개변수 곡선 x=t2−2t,y=√t 그리고 y-축으로 둘러쌓인 영역의 넓이를 구하여라.
문제를 해결하기 위해 주어진 곡선의 넓이를 그린다. (편의를 위해 WolframAlpha 이용하였습니다.)
STEP1. 주어진 매개변수 함수 그리기

위 그림에서 y-축도 함께 둘러쌓인 영역을 확인할 수 있다.
STEP2. 해당 영역에 대한 넓이 공식 적용
이때, y-축으로 둘러쌓인 영역이기 때문에 x \le 0인 영역에 대한 적분으로 이할 수 있다. 따라서, x = t^{2} - 2t = t(t - 2)\le 0인 영역을 의미하기 때문에 0 \le t \le 2에서의 넓이를 구하는 것과 같다.
\begin{align*} A &= \int_{0}^{2} x \; dy \\ &= \int_{0}^{2} (t^{2} -2t) \frac{1}{2\sqrt{t}} \; dt \\ &= \frac{1}{2} \int_{0}^{2} (t^{\frac{3}{2}} - 2t^{\frac{1}{2}}) \; dt \\ &= \frac{1}{2} \left[ \frac{2}{5}t^{\frac{5}{2}} - \frac{4}{3} t^{\frac{3}{2}} \right]_{0}^{2} \\ &= \frac{1}{2} \cdot \left( \frac{4\sqrt{2}}{5} - \frac{4\sqrt{2}}{3} \right) = \frac{8\sqrt{2}}{15} \end{align*}
연습문제8. 매개변수 곡선 x = 1 + e^{t}, y = t - t^{2} 그리고 x-축으로 둘러쌓인 영역의 넓이를 구하여라.
문제를 해결하기 위해 주어진 곡선의 넓이를 그린다. (편의를 위해 WolframAlpha 이용하였습니다.)
STEP1. 주어진 매개변수 함수 그리기

위 그림에서 아주 조금 x-축도 함께 둘러쌓인 영역을 확인할 수 있다.
STEP2. 해당 영역에 대한 넓이 공식 적용
이때, x-축으로 둘러쌓인 영역이기 때문에 y \ge 0인 영역에 대한 적분으로 이할 수 있다. 따라서, y = t - t^{2} = t(1 - t)\le 0인 영역을 의미하기 때문에 0 \le t \le 1에서의 넓이를 구하는 것과 같다.
\begin{align*} A &= \int_{0}^{1} y \; dx \\ &= \int_{0}^{1} (t - t^{2}) e^{t} \; dt \\ &= \int_{0}^{1} (t e^{t} - t^{2} e^{t}) \; dt \end{align*}
위 수식의 두 적분 항에 대해 각각 부분적분법을 적용하여 전개한다.
1). \int_{0}^{1} t e^{t} \; dt
f(t) = t 그리고 g^{'} (t) = e^{t}라고 하자. 따라서 f^{'}(x) = 1 이고 g(x) = e^{t}이다. 부분적분을 통해 아래와 같이 적분할 수 있다.
\begin{align*} \int_{0}^{1} t e^{t} \; dt &= \int f(t) g^{'}(t) \; dx \\ &= \left[ f(t) g(t) \right]_{0}^{1} - \int_{0}^{1} f^{'}(t) g(t) \; dt \\ &= \left[ t e^{t} \right]_{0}^{1} - \int_{0}^{1} e^{t} \; dt \\ &= e - \left[ e^{t} \right]_{0}^{1} \\ &= e - (e - 1) = 1 \end{align*}
2). \int_{0}^{1} t^{2} e^{t} \; dt
f(t) = t^{2} 그리고 g^{'} (t) = e^{t}라고 하자. 따라서 f^{'}(x) = 2t 이고 g(x) = e^{t}이다. 부분적분을 통해 아래와 같이 적분할 수 있다.
\begin{align*} \int_{0}^{1} t^{2} e^{t} \; dt &= \int f(t) g^{'}(t) \; dx \\ &= \left[ f(t) g(t) \right]_{0}^{1} - \int_{0}^{1} f^{'}(t) g(t) \; dt \\ &= \left[ t^{2} e^{t} \right]_{0}^{1} - \int_{0}^{1} 2t e^{t} \; dt = e - 2 \end{align*}
따라서 1)과 2)의 결과를 합치면 주어진 매개변수의 영역에 대한 넓이는 다음과 같이 구할 수 있다.
\begin{align*} A &= \int_{0}^{1} y \; dx \\ &= \int_{0}^{1} (t - t^{2}) e^{t} \; dt \\ &= \int_{0}^{1} (t e^{t} - t^{2} e^{t}) \; dt \\ &= \int_{0}^{1} t e^{t} \; dt - \int_{0}^{1} t^{2} e^{t} \; dt \\ &= 1 - (e - 2) = 3 - e \end{align*}
연습문제9. 주어진 매개변수 곡선들과 t의 범위에 대해 곡선의 길이를 구하는 공식을 세워라. (계산은 하지 않아도 됨)
(a). x = t - t^{2}, y = \frac{4}{3} t^{\frac{3}{2}}, 1 \le t \le 2
(b). x = 1 + e^{t}, y = t^{2}, -3 \le t \le 3
(c). x =t + \cos(t), y = t - \sin(t), 0 \le t \le 2\pi
(d). x = \ln (t), y = \sqrt{t + 1}, 1 \le t \le 5
(a). x = t - t^{2}, y = \frac{4}{3} t^{\frac{3}{2}}, 1 \le t \le 2
\begin{align*} L &= \int_{1}^{2} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{1}^{2} \sqrt{ (1 - 2t)^{2} + (2 t^{\frac{1}{2}})^{2} } \; dt \\ &= \int_{1}^{2} \sqrt{ 4t^{2} - 4t + 5 } \; dt \end{align*}
(b). x = 1 + e^{t}, y = t^{2}, -3 \le t \le 3
\begin{align*} L &= \int_{-3}^{3} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{-3}^{-3} \sqrt{ (e^{t})^{2} + (2t)^{2} } \; dt \\ &= \int_{-3}^{3} \sqrt{ e^{2t} + 4t^{2} } \; dt \end{align*}
(c). x =t + \cos(t), y = t - \sin(t), 0 \le t \le 2\pi
\begin{align*} L &= \int_{0}^{2\pi} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{2\pi} \sqrt{ (1 - \sin(t))^{2} + (1 - \cos(t))^{2} } \; dt \\ &= \int_{0}^{2\pi} \sqrt{ (1 - 2\sin(t) + \sin^{2}(t)) + (1 - 2\cos(t) + \cos^{2}(t)) } \; dt \\ &= \int_{0}^{2\pi} \sqrt{2 - 2\sin(t) - 2\cos(t)} \; dt \end{align*}
(d). x = \ln (t), y = \sqrt{t + 1}, 1 \le t \le 5
\begin{align*} L &= \int_{1}^{5} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{1}^{5} \sqrt{ (\frac{1}{t})^{2} + (\frac{1}{2\sqrt{t + 1}})^{2} } \; dt \\ &= \int_{1}^{5} \sqrt{ \frac{1}{t^{2}} + \frac{1}{4(t + 1)} } \; dt \end{align*}
연습문제10. 주어진 매개변수 곡선들과 t의 범위에 대해 곡선의 길이를 구하라.
(a). x = 1 + 3t^{2}, y = 4 + 2t^{3}, 0 \le t \le 1
(b). x = e^{t} + e^{-t}, y = 5 - 2t, 0 \le t \le 3
(c). x = \frac{t}{1 + t}, y = \ln (1 + t), 0 \le t \le 2
(d). x = 3 \cos(t) - \cos(3t), y = 3 \sin(t) - \sin(3t), 0 \le t \le \pi
(a). x = 1 + 3t^{2}, y = 4 + 2t^{3}, 0 \le t \le 1
\begin{align*} L &= \int_{0}^{1} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} \sqrt{ (6t)^{2} + (6t^{2})^{2} } \; dt \\ &= \int_{0}^{1} \sqrt{ 36t^{2} + 36t^{4} } \; dt \\ &= \int_{0}^{1} 6t \sqrt{1 + t^{2}} \; dt \end{align*}
위 식에서 t = \tan(\theta)라고 하면 dt = \sec^{2}(\theta) d\theta이고 적분구간은 [0, 1] \xrightarrow{\theta = \arctan(t)} [\arctan(0), \arctan(1)] = [0, \frac{\pi}{4}]이다.
\begin{align*} L &= \int_{0}^{1} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} \sqrt{ (6t)^{2} + (6t^{2})^{2} } \; dt \\ &= \int_{0}^{1} \sqrt{ 36t^{2} + 36t^{4} } \; dt \\ &= \int_{0}^{1} 6t \sqrt{1 + t^{2}} \; dt \\ &= 6 \int_{0}^{\frac{\pi}{4}} \tan(\theta) \sqrt{ 1 + \tan^{2} (\theta) } \sec^{2} (\theta) \; d\theta \\ &= 6 \int_{0}^{\frac{\pi}{4}} \tan (\theta) \sec (\theta) \sec^{2} (\theta) \; d\theta \end{align*} - (1)
위 식에서 \sec(\theta) = u라고 하면 \sec(\theta) \tan(\theta) d\theta = du \rightarrow d\theta = \frac{1}{\sec(\theta) \tan(\theta)} du이고 적분구간은 [0, \frac{\pi}{4}] \xrightarrow{u = \sec(\theta)} [\sec(0), \sec(\frac{\pi}{4})] = [1, \sqrt{2}]이다. 이제 (1) 식에서 이어서 쓰면 다음과 같다.
\begin{align*} L &= \int_{0}^{1} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} 6t \sqrt{1 + t^{2}} \; dt \\ &= 6 \int_{0}^{\frac{\pi}{4}} \tan (\theta) \sec (\theta) \sec^{2} (\theta) \; d\theta \\ &= 6 \int_{1}^{\sqrt{2}} \tan(\theta) \sec(\theta) u^{2} \frac{1}{\tan(\theta) \sec(\theta)} \; du \\ &= 6 \int_{1}^{\sqrt{2}} u^{2} \; du \\ &= 6 \left[ \frac{1}{3}u^{3} \right]_{1}^{\sqrt{2}} = 2(2\sqrt{2} - 1) \end{align*}
(b). x = e^{t} + e^{-t}, y = 5 - 2t, 0 \le t \le 3
\begin{align*} L &= \int_{0}^{3} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{3} \sqrt{ (e^{t} - e^{-t})^{2} + (-2)^{2} } \; dt \\ &= \int_{0}^{3} \sqrt{ e^{2t} - 2 + e^{-2t} + 4 } \; dt \\ &= \int_{0}^{3} \sqrt{e^{2t} + 2 + e^{-2t}} \; dt \\ &= \int_{0}^{3} \sqrt{ (e^{t} + e^{-t})^{2} } \; dt \\ &= \int_{0}^{3} (e^{t} + e^{-t}) \; dt \\ &= \left[ e^{t} - e^{-t} \right]_{0}^{3} \\ &= e^{3} - e^{-3} \end{align*}
(c). x = \frac{t}{1 + t}, y = \ln (1 + t), 0 \le t \le 2
\begin{align*} L &= \int_{0}^{2} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{2} \sqrt{ (\frac{1}{(1 + t)^{2}})^{2} + (\frac{1}{1 + t})^{2} } \; dt \\ &= \int_{0}^{2} \sqrt{ \frac{1}{(1 + t)^{4}} (1 + (1 + t)^{2}) } \; dt \\ &= \int_{0}^{2} \frac{1}{(1 + t)^{2}} \sqrt{1 + (1 + t)^{2}} \; dt \end{align*} - (1)
식 (1)에서 1 + t = u라고 하면 dt = du이고 적분구간은 [0, 2] \xrightarrow{u = t + 1} [1, 3]이다. 이제 (1) 식에서 이어서 쓰면 다음과 같다.
\begin{align*} L &= \int_{0}^{2} \frac{1}{(1 + t)^{2}} \sqrt{1 + (1 + t)^{2}} \; dt \\ &= \int_{1}^{3} \frac{1}{u^{2}} \sqrt{1 + u^{2}} \; du \\ &= \int_{1}^{3} \frac{\sqrt{1 + u^{2}}}{u^{2}} \end{align*} - (2)
식 (2)에서 f(u) = \sqrt{1 + u^{2}} 그리고 g^{'} (u) = \frac{1}{u^{2}}라고 하자. 따라서 f^{'}(u) = \frac{u}{\sqrt{1 + u^{2}}} 이고 g(u) = -\frac{1}{u}이다. 부분적분을 통해 식 (2)는 다음과 같이 적분할 수 있다.
\begin{align*} L &= \int_{1}^{3} \frac{\sqrt{1 + u^{2}}}{u^{2}} \; du \\ &= \int_{1}^{3} f(u) g^{'}(u) \; du \\ &= \left[ f(u) g(u) \right]_{1}^{3} - \int_{1}^{3} f^{'}(u) g(u) \; du \\ &= \left[ -\frac{\sqrt{1 + u^{2}}}{u} \right]_{1}^{3} - \int_{1}^{3} \frac{u}{\sqrt{1 + u^{2}}} \cdot \left( -\frac{1}{u} \right) \; dt \\ &= \left( \sqrt{2} - \frac{1}{3}\sqrt{10} \right) + \int_{1}^{3} \frac{1}{\sqrt{1 + u^{2}}} \; du \end{align*} - (3)
식 (3)의 두 개의 적분항 중 두번째 항은 u = \tan(\theta)라고 하면 du = \sec^{2} (\theta) d\theta이고 적분구간은 [1, 3] \xrightarrow{\theta = \arctan (u)} [\arctan(1), \arctan(3)] = [\frac{\pi}{4}, \alpha]이다. 여기서, \alpha = \arctan(3)이다. 따라서 적분항은 다음과 같이 적분할 수 있다.
\begin{align*} \int_{1}^{3} \frac{1}{\sqrt{1 + u^{2}}} \; du &= \int_{\frac{\pi}{4}}^{\alpha} \frac{1}{\sqrt{1 + \tan^{2} (\theta)}} \cdot \sec^{2} (\theta) \; d\theta \\ &= \int_{\frac{\pi}{4}}^{\alpha} \frac{1}{\sec(\theta)} \cdot \sec^{2} (\theta) \; d\theta \\ &= \int_{\frac{\pi}{4}}^{\alpha} \sec(\theta) \; d\theta \\ &= \left[ \ln | \sec(\theta) + \tan(\theta) | \right]_{\frac{\pi}{4}}^{\alpha} \end{align*} - (4)
식 (4)에서 u = \tan(\theta)임을 고려하면 \sec(\theta) = \sqrt{u^{2} + 1}과 동일하므로 다시 u에 대한 적분으로 다음과 같이 표현할 수 있다.
\begin{align*} \int_{1}^{3} \frac{1}{\sqrt{1 + u^{2}}} \; du &= \left[ \ln | \sec(\theta) + \tan(\theta) | \right]_{\frac{\pi}{4}}^{\alpha} \\ &= \left[ \ln | \sqrt{u^{2} + 1} + u | \right]_{1}^{3} = \ln (\sqrt{10} + 3) - \ln (\sqrt{2} + 1) \end{align*} - (5)
이제 식 (5)의 결과를 식 3에 더하면 최종 곡선의 길이를 얻을 수 있다.
\begin{align*} L &= \left( \sqrt{2} - \frac{1}{3}\sqrt{10} \right) + \int_{1}^{3} \frac{1}{\sqrt{1 + u^{2}}} \; du = \left( \sqrt{2} - \frac{1}{3} \sqrt{10} \right) + \left( \ln (\sqrt{10} + 3) - \ln (\sqrt{2} + 1) \right) \end{align*}
(d). x = 3 \cos(t) - \cos(3t), y = 3 \sin(t) - \sin(3t), 0 \le t \le \pi
\begin{align*} L &= \int_{0}^{\pi} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{\pi} \sqrt{ (-3\sin(t) + 3\sin(3t))^{2} + (3\cos(t) - 3\cos(t))^{2} } \; dt \\ &= \int_{0}^{\pi} \sqrt{ (9\sin^{2} (t) - 18\sin(t)\sin(3t) + 9\sin^{2} (3t)) + (9\cos^{2} (t) - 18\cos(t)\cos(3t) + 9\cos^{2}(3t)) } \; dt \\ &= \int_{0}^{\pi} \sqrt{9 (\sin^{2} (t) + \cos^{2} (t)) + 9 (\sin^{2} (3t) + \cos^{2} (3t)) - 18 (\sin(t)\sin(3t) + \cos(t)\cos(3t))} \; dt \\ &= \int_{0}^{\pi} \sqrt{ 18 - 18\cos(2t) } \; dt \\ &= \int_{0}^{\pi} \sqrt{18} \sqrt{1 - (1 - 2\sin^{2} (t))} \; dt \\ &= \int_{0}^{\pi} \sqrt{36} \sqrt{\sin^{2} (t)} \; dt \\ &= 6 \int_{0}^{\pi} \sin(t) \; dt \\ &= 6 \left[ -\cos(t) \right]_{0}^{\pi} = 6 \cdot 2 = 12 \end{align*}
연습문제11. 매개변수 곡선 x = 3t - t^{3}, y = 3t^{2}의 루프의 길이를 구하여라.
문제를 해결하기 위해 주어진 곡선의 넓이를 그린다. (편의를 위해 WolframAlpha 이용하였습니다.)
STEP1. 주어진 매개변수 함수 그리기

위 그림에서 루프가 생긴 지점을 확인할 수 있다. 즉, x(t) = 0이 되는 지점을 의미한다.
STEP2. 해당 매개변수 곡선에 대한 길이 공식 적용
이때, t의 범위는 x(t) = 0이 되는 지점의 시작점과 끝점이다. 따라서, x(t) = 3t - t^{3} = t(\sqrt{3} - t)(\sqrt{3} + t) = 0이라고 하면 t = 0 그리고 t = \pm \sqrt{3}에서 x(t) = 0이다. 따라서, 전체 루프는 t = -\sqrt{3}부터 t = \sqrt{3}에서 라고 할 수 있다. 이제 곡선의 길이를 다음과 같이 구할 수 있다.
\begin{align*} L &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{ (3 - 3t^{2})^{2} + ( 6t )^{2} } \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{9 - 18t^{2} + 9t^{4} + 36t^{2}} \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{9 + 18t^{2} + 9t^{4}} \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{(3 + 3t^{2})^{2}} \; dt \\ &= \int_{-\sqrt{3}}^{\sqrt{3}} (3 + 3t^{2}) \; dt \\ &= 2 \int_{0}^{\sqrt{3}} (3 + 3t^{2}) \; dt \\ &= 2 \left[ 3t + t^{3} \right]_{0}^{\sqrt{3}} = 12\sqrt{3} \end{align*}
연습문제12. 주어진 매개변수 곡선들과 t의 범위에 대해서 x축을 중심으로 회전했을 때 얻을 수 있는 회전체의 겉넓이에 대한 공식을 세워라. (계산은 하지 않아도 됨)
(a). x = 1 + te^{t}, y = (t^{2} + 1) e^{t}, 0 \le t \le 1
(b). x = \sin^{2} (t), y = \sin(3t), 0 \le t \le \frac{\pi}{3}
(a). x = 1 + te^{t}, y = (t^{2} + 1) e^{t}, 0 \le t \le 1
\begin{align*} S &= \int_{0}^{1} 2\pi y \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} 2 \pi (t^{2} + 1) e^{t} \sqrt{ (e^{t} + te^{t})^{2} + (2t e^{t} + (t^{2} + 1) e^{t})^{2} } \; dt \\ &= \int_{0}^{1} 2 \pi (t^{2} + 1) e^{t} \sqrt{ \left[ (1 + t) e^{t} \right]^{2} + \left[ (t + 1)^{2}e^{t} \right]^{2} } \; dt \end{align*}
(b). x = \sin^{2} (t), y = \sin(3t), 0 \le t \le \frac{\pi}{3}
\begin{align*} S &= \int_{0}^{\frac{\pi}{3}} 2\pi y \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{\frac{\pi}{3}} 2 \pi \sin (3t) \sqrt{ (2\sin(t)\cos(t))^{2} + (3\cos(3t))^{2} } \; dt \\ &= \int_{0}^{\frac{\pi}{3}} 2 \pi \sin(3t) \sqrt{ \sin^{2} (2t) + 9\cos^{2} (3t) } \; dt \end{align*}
연습문제13. 주어진 매개변수 곡선들과 t의 범위에 대해서 x축을 중심으로 회전했을 때 얻을 수 있는 회전체의 겉넓이를 구하여라.
(a). x = 3t - t^{3}, y = 3t^{2}, 0 \le t \le 1
(b). x = a\cos^{3} (\theta), y = a \sin^{3} (\theta), 0 \le \theta \le \frac{\pi}{2}
(a). x = 3t - t^{3}, y = 3t^{2}, 0 \le t \le 1
\begin{align*} S &= \int_{0}^{1} 2\pi y \sqrt{\left( \frac{dx}{dt} \right)^{2} + \left( \frac{dy}{dt} \right)^{2}} \; dt \\ &= \int_{0}^{1} 2 \pi 3t^{2} \sqrt{ (3 - 3t^{2})^{2} + (6t)^{2} } \; dt \\ &= \int_{0}^{1} 2 \pi 3t^{2} \sqrt{ (9 - 18t^{2} + 9t^{4}) + 36t^{2} } \; dt \\ &= \int_{0}^{1} 2 \pi 3t^{2} \sqrt{9t^{4} + 18t^{2} + 9} \; dt \\ &= \int_{0}^{1} 2\pi 3t^{2} \sqrt{(3t^{2} + 3)^{2}} \; dt \\ &= \int_{0}^{1} 2\pi 3t^{2} (3t^{2} + 3) \; dt \\ &= \int_{0}^{1} 2\pi 3t^{2} (3t^{2} + 3) \; dt \\ &= 2\pi \int_{0}^{1} (9t^{4} + 9t^{2}) \; dt \\ &= 18\pi \left[ \frac{1}{5} t^{5} + \frac{1}{3} t^{3} \right]_{0}^{1} = 18\pi \left( \frac{1}{5} + \frac{1}{3} \right) = \frac{144\pi}{15} \end{align*}
(b). x = a\cos^{3} (\theta), y = a \sin^{3} (\theta), 0 \le \theta \le \frac{\pi}{2}
\begin{align*} S &= \int_{0}^{\frac{\pi}{2}} 2\pi y \sqrt{\left( \frac{dx}{dt\theta} \right)^{2} + \left( \frac{dy}{d\theta} \right)^{2}} \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2 \pi a \sin^{3} (\theta) \sqrt{ (-3a\sin(\theta)\cos^{2}(\theta))^{2} + (3a\sin^{2}(\theta)\cos(\theta))^{2} } \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2 \pi a\sin^{3} (\theta) \sqrt{ 9a^{2}\sin^{2}(\theta)\cos^{4}(\theta) + 9a^{2}\sin^{4}(\theta)\cos^{2}(\theta) } \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2 \pi a\sin^{3} (\theta) \sqrt{9a^{2}\sin^{2}(\theta)\cos^{2}(\theta) (\sin^{2} (\theta) + \cos^{2} (\theta))} \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2\pi 3a\sin^{3}(\theta) \sqrt{(3a\sin(\theta)\cos(\theta))^{2}} \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} 2\pi (3a\sin^{3} (\theta)) (3a\sin(\theta)\cos(\theta)) \; d\theta \\ &= 6a^{2}\pi \int_{0}^{\frac{\pi}{2}} \sin^{4} (\theta)\cos(\theta) \; d\theta \end{align*} - (1)
식 (1)에서 \sin(\theta) = u라고 하면 \cos(\theta) d\theta = du \rightarrow d\theta = \frac{1}{\cos(\theta)} du이고 적분구간은 [0, \frac{\pi}{2}] \xrightarrow{u = \sin(\theta)} [0, 1]이다. 이제 (1) 식에서 이어서 쓰면 다음과 같다.
\begin{align*} S &= 6a^{2}\pi \int_{0}^{\frac{\pi}{2}} \sin^{4} (\theta)\cos(\theta) \; d\theta \\ &= 6a^{2} \pi \int_{0}^{1} u^{4} \cos(\theta) \frac{1}{\cos(\theta)} \; du \\ &= 6a^{2}\pi \int_{0}^{1} u^{4} \; du = 6a^{2} \pi \left[ \frac{1}{5} u^{5} \right]_{0}^{1} = \frac{6}{5}a^{2}\pi \end{align*}
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 극좌표계 곡선 (0) | 2022.04.09 |
|---|---|
| 미적분학 - 극좌표계 (0) | 2022.04.08 |
| 미적분학 - 매개변수 함수 (0) | 2022.04.02 |
| 미적분학 - 일 (1) | 2022.03.30 |
| 미적분학 - 회전체의 겉넓이 (2) | 2022.03.29 |
