안녕하세요. 지난 포스팅의 미적분학 - 일에서는 적분을 물리학에 응용하는 방법에 대해서 알아보았습니다. 지금까지 저희는 극한, 미분, 적분을 통해 기본적인 미적분학의 지식은 갖추었습니다. 이제부터는 조금 더 어려운 응용 단계를 진행을 해보고자 합니다. 오늘은 이를 위한 첫번째 단계로 매개변수 함수(Parametric Function)에 대해서 다루어보도록 하겠습니다.

위와 같은 그래프로 이루어진 어떤 함수가 있다고 가정하겠습니다. 굉장히 복잡하게 생겼네요. 아쉽게도 위 그래프를 $y = f(x)$ 꼴의 형태로 표현하는 것은 불가능합니다. 하지만, $x$ 방향과 $y$ 방향이 각각 어떤 함수를 따른다고 가정을 한다면 충분히 가능하죠. 이 말은 $x = f(t), y = g(t)$와 같이 $x, y$ 축이 각각 새로운 매개변수(parameter) $t$에 의해 정의된다는 것을 의미합니다. 여기서, $(x, y)$를 결정하는 요소는 $t$임을 주목하시길 바랍니다. 따라서 저희는 곡선 $C$를 아래와 같이 쓸 수 있습니다.
$$C : (x, y) = (f(t), g(t))$$
그리고 만약, $a \le t \le b$라면 $(f(a), g(a))$를 매개변수 곡선의 시점(initial point), $(f(b), g(b))$를 종점(terminal point)라고 합니다.
매개변수 함수는 이와 같이 간단한 정의입니다. 하지만, 매개변수 함수 중 굉장히 중요하게 다루어지는 함수가 있는데요. 오늘은 추가적으로 사이클로이드(Cycloid)에 대해서도 다루어보도록 하겠습니다.


사이클로이드는 위와 같은 궤적을 가지는 곡선입니다. 원이 원점 $O$에서 시작하고 시계방향으로 회전한다고 가정하겠습니다. 그러면 임의의 시점에 대응되는 점 $P$를 매개변수로 표현할 수 있을까요? 일단, $\bar{OT}$부터 생각해보겠습니다. 이 선분의 길이는 호 $\bar{PT}$의 길이와 완전히 일치합니다. 따라서, $\bar{OT} = \bar{PT} = r\theta$입니다. 따라서, 원의 중심은 $C(r\theta, r)$이 될 겁니다.
다음으로 할 것은 점 $P$를 $(x, y)$라고 하겠습니다. 그러면, 각 점은 아래와 같이 구할 수 있습니다.
$$x = |OT| - |PQ| = r\theta - r\sin(\theta) = r(\theta - \sin(\theta))$$
$$y = |CT| - |CQ| = r - r\cos(\theta) = r(1 - \cos(\theta))$$
그러므로 사이클로이드의 매개변수 함수는 아래와 같습니다.
$$C : (x, y) = (r(\theta - \sin(\theta)), r(1 - \cos(\theta)))$$
연습문제1. 주어진 매개방정식들의 그래프를 그리시오.
(a). $x = 1 + \sqrt{t}, y = t^{2} - 4t, 0 \le t \le 5$
(b). $x = 2\cos(t), y = t - \cos(t), 0 \le t \le 2\pi$
(c). $x = 5\sin(t), y = t^{2}, -\pi \le t \le \pi$
(d). $x = e^{-t} + t, y = e^{t} - t, -2 \le t \le 2$
(a). $x = 1 + \sqrt{t}, y = t^{2} - 4t, 0 \le t \le 5$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | 0 | 1 | 2 | 3 | 4 | 5 |
| $x(t)$ | 1 | 2 | 1 + $\sqrt{2}$ | 1 + $\sqrt{3}$ | 3 | 1 + $\sqrt{5}$ |
| $y(t)$ | 0 | -3 | -4 | -3 | 0 | 5 |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.
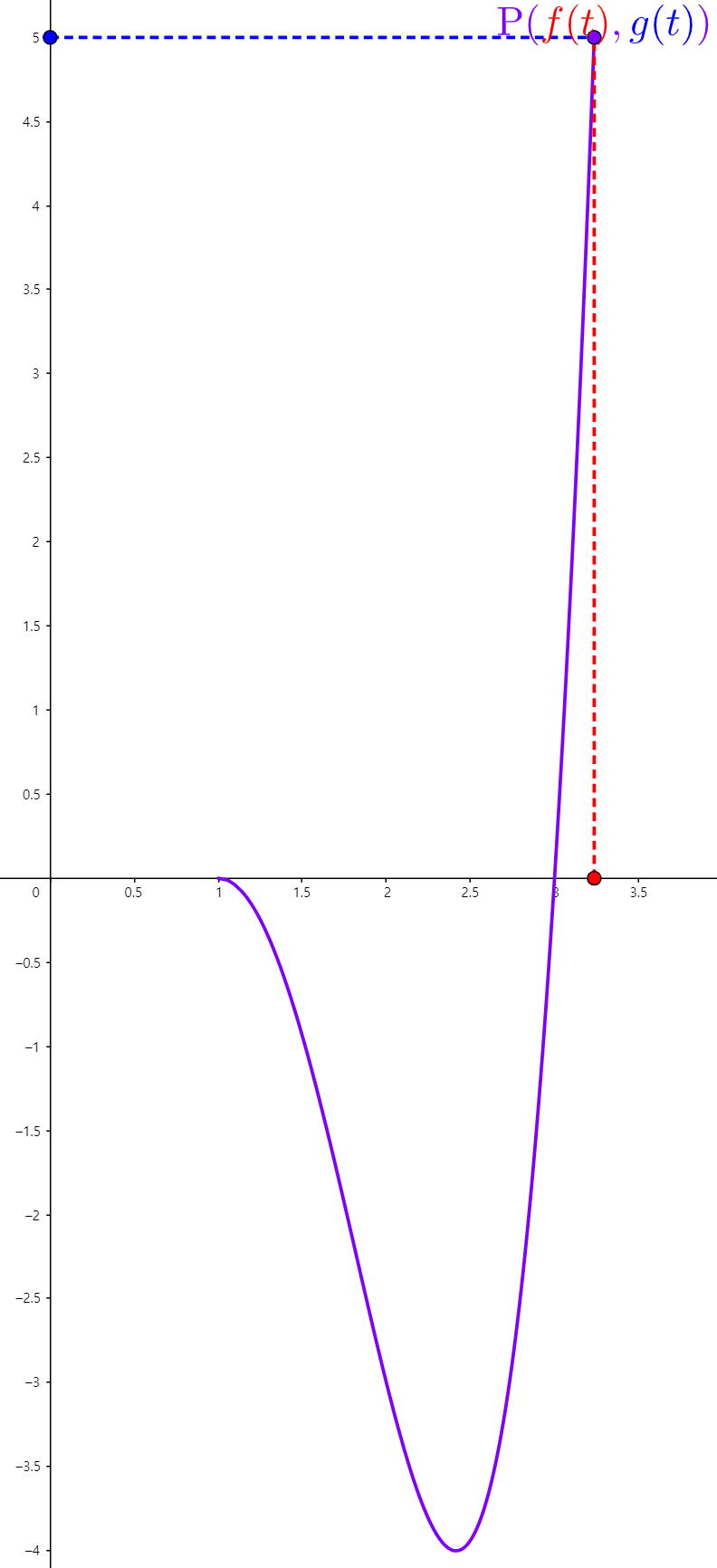
(b). $x = 2\cos(t), y = t - \cos(t), 0 \le t \le 2\pi$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | 0 | $\frac{\pi}{2}$ | $\pi$ | $\frac{3\pi}{2}$ | $2\pi$ |
| $x(t)$ | 2 | 0 | -2 | 0 | 2 |
| $y(t)$ | -1 | $\frac{\pi}{2}$ | $\pi$ + 1 | $\frac{3\pi}{2}$ | $2\pi$ - 1 |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.

(c). $x = 5\sin(t), y = t^{2}, -\pi \le t \le \pi$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | $-\pi$ | $-\frac{\pi}{2}$ | 0 | $\frac{\pi}{2}$ | $\pi$ |
| $x(t)$ | 0 | -5 | 0 | 5 | 0 |
| $y(t)$ | $\pi^{2}$ | $\frac{\pi^{2}}{4}$ | 0 | $\frac{\pi^{2}}{4}$ | $\pi^{2}$ |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.

(d). $x = e^{-t} + t, y = e^{t} - t, -2 \le t \le 2$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | -2 | -1 | 0 | 1 | 2 |
| $x(t)$ | $e^{2}$ - 2 | $e$ - 1 | 1 | $e^{-1} + 1$ | $e^{-2} + 2$ |
| $y(t)$ | $e^{-2} + 2$ | $e^{-1} + 1$ | 1 | $e - 1$ | $e^{2} - 2$ |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.

연습문제2. 주어진 매개변수 방정식의 그래프를 그리고 매개변수를 없앤 카르테시안 방정식 형태를 구하시오.
(a). $x = 3t - 5, y = 2t + 1$
(b). $x = 1 + t, y = 5 - 2t, -2 \le t \le 3$
(c). $x = t^{2} - 2, y = 5 - 2t, -3 \le t \le 4$
(d). $x = 1 + 3t, y = 2 - t^{2}$
(e). $x = \sqrt{t}, y = 1 - t$
(f). $x = t^{2}, y = t^{3}$
(a). $x = 3t - 5, y = 2t + 1$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | -2 | -1 | 0 | 1 | 2 |
| $x(t)$ | -11 | -8 | -5 | -2 | 1 |
| $y(t)$ | -3 | -1 | 1 | 3 | 5 |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.
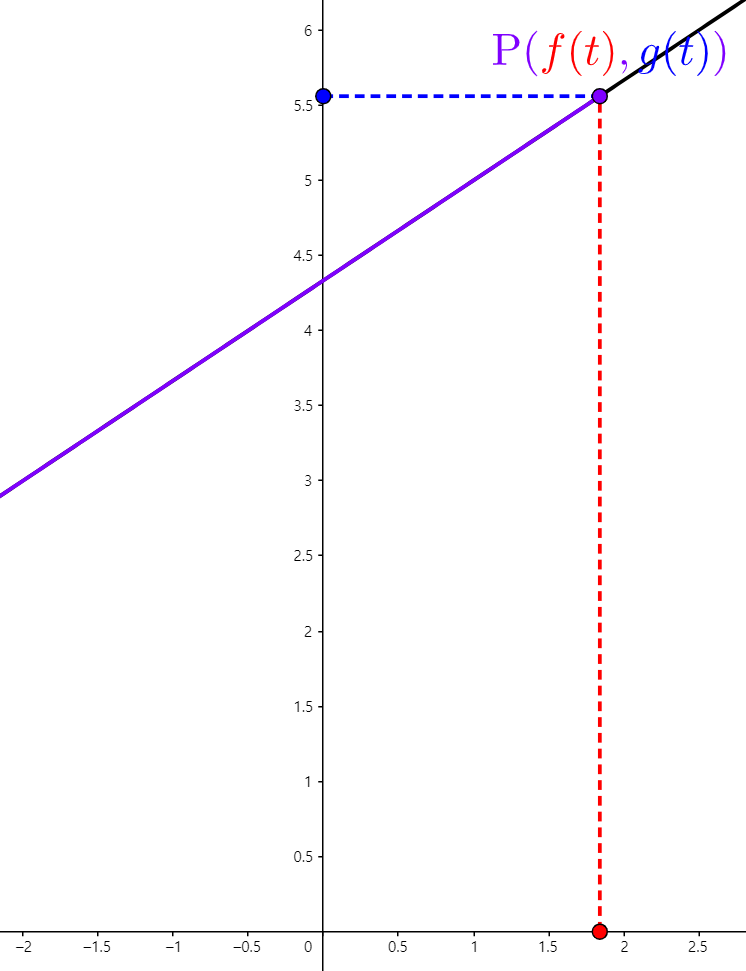
STEP3. 카르테시안 방정식으로 변환한다.
$$\begin{align*} x = 3t - 5 \rightarrow t = \frac{1}{3} (x + 5) \end{align*}$$
이를 $y(t)$에 대입하면 다음과 같다.
$$\begin{align*} y &= 2t + 1 \\ &= \frac{2}{3} (x + 5) + 1\\ &= \frac{2}{3}x + \frac{13}{3} \end{align*}$$
(b). $x = 1 + t, y = 5 - 2t, -2 \le t \le 3$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | -2 | -1 | 0 | 1 | 2 | 3 |
| $x(t)$ | -1 | 0 | 1 | 2 | 3 | 4 |
| $y(t)$ | 9 | 7 | 5 | 3 | 1 | -1 |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.

STEP3. 카르테시안 방정식으로 변환한다.
$$\begin{align*} x = 1 + t \rightarrow t = 1 - x \end{align*}$$
이를 $y(t)$에 대입하면 다음과 같다.
$$\begin{align*} y &= 5 - 2t \\ &= 5 - 2(1 - x) \\ &= 5 - 2 + 2x \\ &= 2x + 3 \end{align*}$$
(c). $x = t^{2} - 2, y = 5 - 2t, -3 \le t \le 4$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| $x(t)$ | 7 | 1 | -1 | -2 | -1 | 2 | 7 | 14 |
| $y(t)$ | 11 | 9 | 7 | 5 | 3 | 1 | -1 | -3 |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.

STEP3. 카르테시안 방정식으로 변환한다.
$$\begin{align*} y = 5 - 2t \rightarrow t = \frac{1}{2} (5 - y) \end{align*}$$
이를 $x(t)$에 대입하면 다음과 같다.
$$\begin{align*} x &= t^{2} - 2 \\ &= \frac{1}{4}(5 - t)^{2} - 2 \end{align*}$$
(d). $x = 1 + 3t, y = 2 - t^{2}$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | -2 | -1 | 0 | 1 | 2 |
| $x(t)$ | -5 | -2 | 1 | 4 | 7 |
| $y(t)$ | -2 | 1 | 2 | 1 | -2 |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.
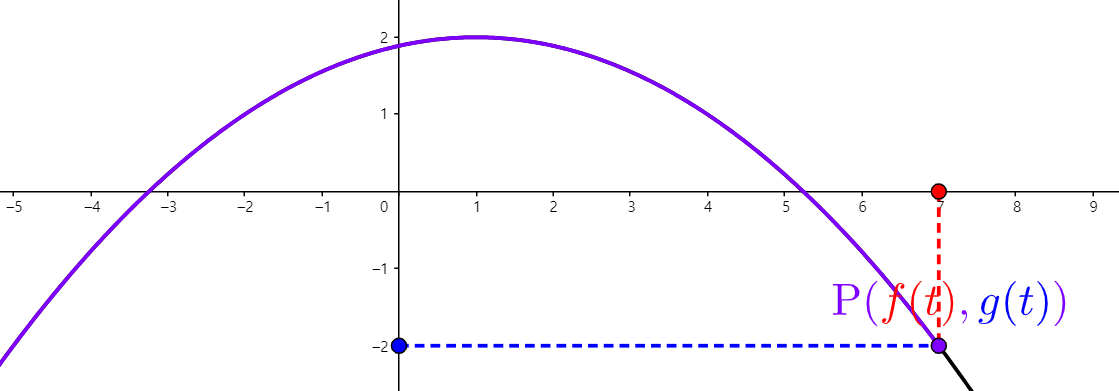
STEP3. 카르테시안 방정식으로 변환한다.
$$\begin{align*} x = 1 + 3t \rightarrow t = \frac{1}{3} (x - 1) \end{align*}$$
이를 $y(t)$에 대입하면 다음과 같다.
$$\begin{align*} y &= 2 - t^{2} \\ &= 2 - \frac{1}{9}(x - 1)^{2} \end{align*}$$
(e). $x = \sqrt{t}, y = 1 - t$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | 0 | 1 | 2 | 3 | 4 |
| $x(t)$ | 0 | 1 | $\sqrt{2}$ | $\sqrt{3}$ | 2 |
| $y(t)$ | 1 | 0 | -1 | -2 | -3 |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.

STEP3. 카르테시안 방정식으로 변환한다.
$$\begin{align*} x = \sqrt{t} \rightarrow t = x^{2} \end{align*}$$
이를 $y(t)$에 대입하면 다음과 같다.
$$\begin{align*} y &= 1 - t \\ &= 1 - x^{2} \end{align*}$$
(f). $x = t^{2}, y = t^{3}$
STEP1. 주어진 범위 내에서 계산하기 쉬운 $t$ 점을 선택하여 $(x, y)$를 표로 나타낸다. (이때, 시작점과 끝점은 반드시 포함시킨다.)
| $t$ | -2 | -1 | 0 | 1 | 2 |
| $x(t)$ | 4 | 1 | 0 | 1 | 4 |
| $y(t)$ | -8 | -1 | 0 | 1 | 8 |
STEP2. 표를 통해 얻은 점들을 순서대로 이어준다.
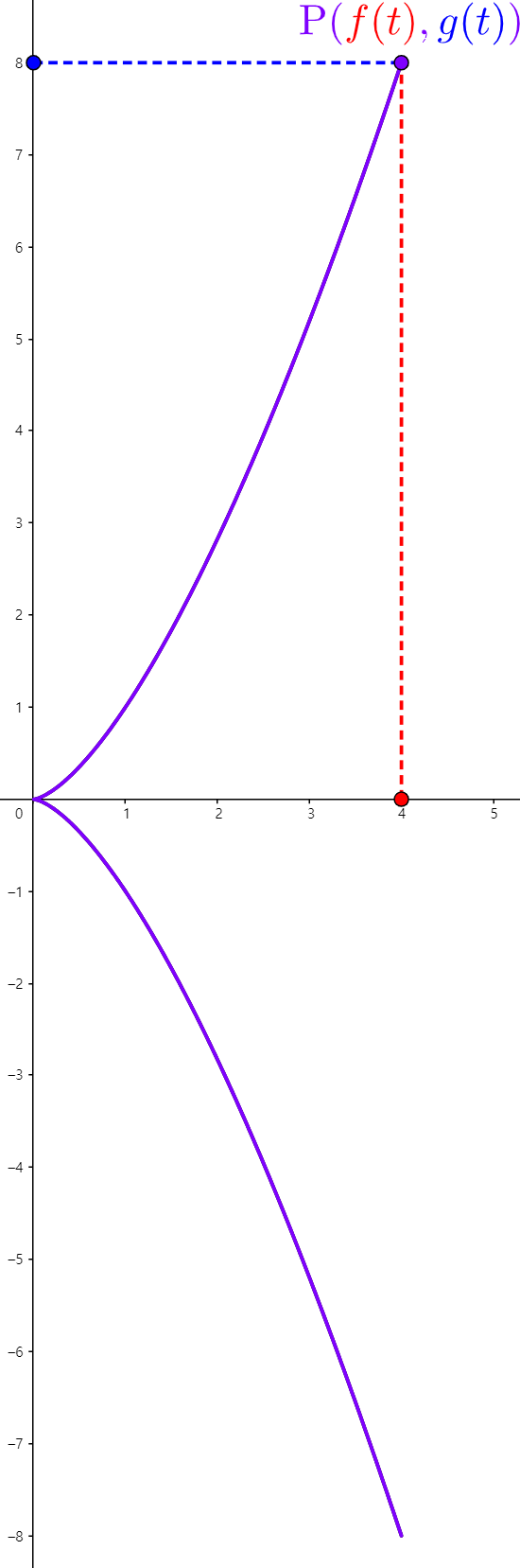
STEP3. 카르테시안 방정식으로 변환한다.
$$\begin{align*} x = t^{2} \rightarrow t = \sqrt{x} \end{align*}$$
이를 $y(t)$에 대입하면 다음과 같다.
$$\begin{align*} y &= t^{3} \\ &= x^{\frac{3}{2}} \end{align*}$$
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 극좌표계 (0) | 2022.04.08 |
|---|---|
| 미적분학 - 매개변수와 미적분학 (0) | 2022.04.06 |
| 미적분학 - 일 (1) | 2022.03.30 |
| 미적분학 - 회전체의 겉넓이 (2) | 2022.03.29 |
| 미적분학 - 곡선의 길이 (0) | 2022.03.27 |
