안녕하세요. 이번 카테고리는 미적분학(Calculus)에 대해서 설명하고자 합니다. 미적분학은 물리학 현상(자유 낙하 운동, ...), 생물학(박테리아 증식 방정식, 생물 군집 특성 분석, ...), 사회학 등 많은 분야에서 활용되고 있어 사실 상 모든 대학교의 기본 과목으로 생각하시면 될 거 같습니다. 저 역시 수학과를 나왔기에 미적분학을 가장 먼저 수강하여 재밌게 들었던 기억이 있습니다. 하지만, 신입생 이후로 직접적으로 미적분학을 사용할 일이 없다가 대학원에 입학하니 미적분학에 대한 기초 개념이 필요하게 되었습니다. 그렇게 다시 공부를 하고자 이번 카테고리를 만들었으니 혹시 궁금하신 점이나 틀린 점이 있다면 지적 부탁드립니다.
오늘은 가장 처음이기 때문에 앞으로 배울 모든 내용의 주제가 되는 "함수(Function)"에 대해서 다루어보겠습니다. 사실 함수라는 하나의 주제만 해도 두꺼운 책을 쓸 수 있을 정도로 넓은 주제가 있습니다. 하지만 모든 범위를 다루기에는 제 지식도 얕을뿐만 아니라 흥미도 잃을 거 같아서 가벼운 주제만 정리하도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
1. 함수의 정의
정의1. 함수(Functions)
함수 $f$는 집합 $D$의 각 원소 $x$가 정확히 집합 $E$의 1개의 원소 $f(x)$에 대응되는 규칙이다.
설명
위와 같이 "함수 = 규칙"입니다. 여기서 몇 가지 용어를 정리하도록 하겠습니다.
- 정의역(Domain) $D = \text{dom}(f)$ : 함수 $f$의 모든 입력값의 집합
- 공역(Codomain) $E$ : 함수 $f$의 모든 가능한 출력값의 집합
- 치역(Range) $R \subseteq E$ : 함수 $f$의 정의역 $D$가 $f$에 의해 대응되는 모든 원소 $f(x)$의 집합
- 독립 변수(Independent variable) : 정의역 $D$의 임의의 원소
- 종속 변수(Dependent variable) : 치역 $R$의 임의의 원소
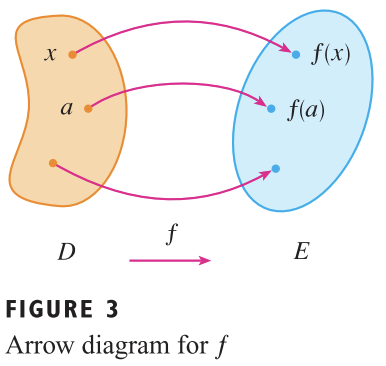
이 용어들은 모든 수학 분야에서 나오기 때문에 꼭 알아두어야 하는 개념입니다. 이를 그림으로 표현하면 아래와 같습니다.
예제1. $f(x) = 2x - 1, g(x) = x^{2}, h(x) = \sqrt{x}$의 정의역, 공역, 치역을 찾아라.
1). $f(x) = 2x - 1$를 그림으로 그려본다.
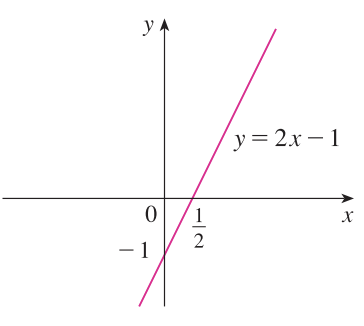
$f$의 정의역에는 특별한 조건이 없기 때문에 실수 전체 집합, 즉 $D = \mathbb{R}$이다. 공역 역시 모든 실수를 고려하기 때문에 $E = \mathbb{R}$이다. 마지막으로 치역은 함수 $f(x)$에 $D$의 모든 원소를 입력했을 때 모든 실수로 대응시킬 수 있기 때문에 $R = \mathbb{R}$이다.
$$D = E = R = \mathbb{R}$$
2). $g(x) = x^{2}$을 그림으로 그려본다.
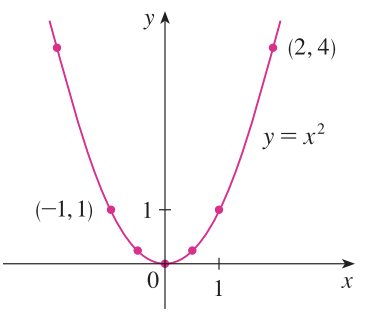
$g$의 정의역에는 특별한 조건이 없기 때문에 실수 전체 집합, 즉 $D = \mathbb{R}$이다. 공역 역시 모든 실수를 고려하기 때문에 $E = \mathbb{R}$이다. 마지막으로 치역은 함수 $g(x)$에 $D$의 모든 원소를 입력했을 때 0을 포함하는 양의 실수로 대응시킬 수 있기 때문에 $R = \mathbb{R}_{+}$이다. 여기서 $\mathbb{R}_{+}$는 0이상의 모든 실수 집합을 의미한다.
$$D = E = \mathbb{R}, R = \mathbb{R}_{+}$$
3). $h(x) = \sqrt{x}$는 정의역의 조건이 루트 내의 실수는 항상 양수여야한다는 조건이 있기 때문에 $D = \mathbb{R}_{+}$이다. 그리고 기본적으로 공역은 모든 실수를 고려하기 때문에 $E = \mathbb{R}$이다. 마지막으로 치역은 $D$의 모든 원소를 입력했을 때 0을 포함하는 양의 실수로 대응시키기 때문에 $R = \mathbb{R}_{+}$이다.
$$D = R = \mathbb{R}_{+}, E = \mathbb{R}$$
또한 함수에는 위의 예시처럼 매끄럽게 1개의 함수로만 이루어진 경우도 있지만, 여러 개의 함수가 구간별로 정의된 경우도 있습니다. 이를 "조각함수(piecewise function)"라고 부릅니다. 가장 대표적인 조각 함수가 바로 절댓값 함수입니다.
$$f(x) = \left|x\right| = \begin{cases} x &x \ge 0 \\ -x &x < 0\end{cases}$$
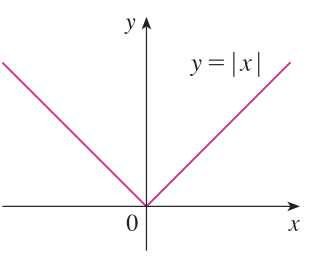
절댓값 함수는 정의역이 양수라면 $x$, 음수라면 $-x$를 출력으로 뱉는 함수입니다. 이와 같이 특정 구간별로 다른 함수로 정의될 수 있습니다.
만약 함수에 대한 더욱 수학적인 내용이 궁금하시다면 집합론 - 함수를 참조해주시길 바랍니다.
2. 함수의 대칭성
다음으로 함수를 대칭성에 따라서 짝함수(even function), 기함수(odd function)으로 구분할 수 있습니다. 간단하게 짝함수는 $y$축에 대칭인 함수, 기함수는 원점 $(0, 0)$에 대칭인 함수를 의미합니다. 가장 대표적인 짝함수는 $f(x) = x^{2}$, 기함수는 $g(x) = x$입니다. 그리고 짝함수와 기함수를 판별하는 가장 쉬운 방법은 $x$ 대신에 $-x$를 넣어보는 것입니다. $f(-x) = f(x)$라면 $f(x)$는 짝함수, $f(-x) =-f(x)$이라면 $f(x)$는 기함수입니다. 예를 들어서 $f(-x) = (-x)^{2} = x^{2} = f(x)$이기 때문에 $f(x)$는 짝함수, $g(-x) = -x = -g(x)$이기 때문에 $g(x) = x$는 기함수입니다.
예제2.$f(x) = x^{5} + x, g(x) = 1 - x^{4}$가 짝함수인지, 기함수인지 판별하라
1). $f(-x) = (-x)^{5} + (-x) = -(x^{5} + x) = -f(x) \Rightarrow f(x)$는 기함수이다.
2). $g(-x) = 1 - (-x)^{4} = 1 - x^{4} = g(x) \Rightarrow g(x)$는 우함수이다.
3. 함수의 증감
정의2. 증가함수(increase function)와 감소함수(decrease function)
- 함수 $f$가 범위 $I$의 $x_{1} < x_{2}$를 만족하는 $x_{1}, x_{2}$에 대해서 $f(x_{1}) < f(x_{2})$가 성립하면 $f$는 증가함수이다.
- 함수 $f$가 범위 $I$의 $x_{1} < x_{2}$를 만족하는 $x_{1}, x_{2}$에 대해서 $f(x_{1}) > f(x_{2})$가 성립하면 $f$는 감소함수이다.
연습문제1. 아래와 같은 함수 그래프가 주어졌다고 할 때 물음에 답하여라.
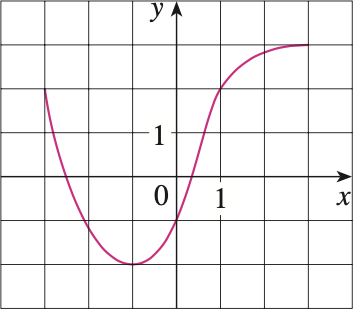
(a). $f(-1)$의 값은 무엇인가?
(b). $f(x) = 2$일 때, $x$의 값은 무엇인가?
(c). $f$의 증가하는 구간은 어디인가?
(a). $f(-1) = -2$
(b). $f(x) = 2$일 때, $x = 1$과 $x = -3$
(c). $[-1, 3]$에서 함수 $f$는 증가한다.
연습문제2. 아래와 같은 함수 그래프가 주어졌다고 할 때 물음에 답하여라.
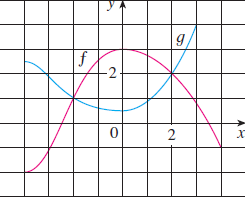
(a). $f(-4)$와 $g(3)$의 값은 무엇인가?
(b). $f(x) = g(x)$를 만족하는 $x$의 값은 무엇인가?
(c). $f$의 감소하는 구간은 어디인가?
(d). $f$와 $g$의 정의역과 치역은 어디인가?
(a). $f(-4) = -2, f(3) = 4$
(b). $x = \pm 2$
(c). $[0, 4]$
(d). 함수 $f$의 정의역과 치역 :$D_{f} = [-4, 4], R_{f} = [-2, 3]$
함수 $g$의 정의역과 치역 : $D_{g} = [-4, 3], R_{g} = [0.5, 4]$
연습문제3. 아래 4개의 그래프 중 함수인지 판별하고 함수라면 정의역과 치역을 구하여라.
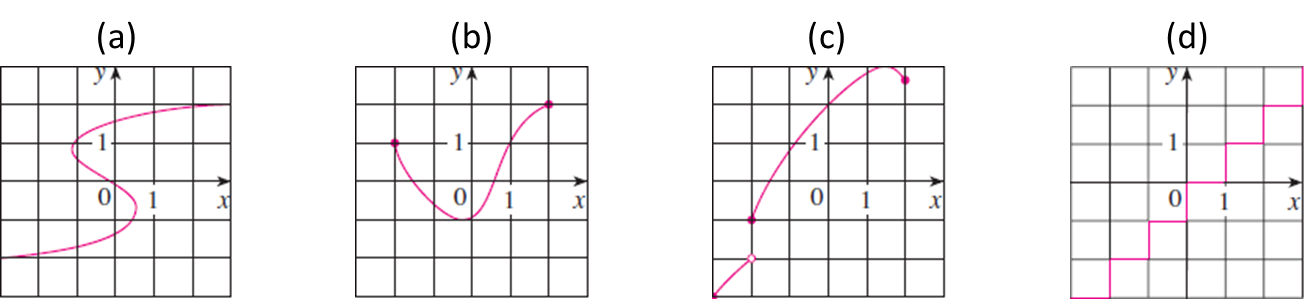
정의1의 함수의 정의에 따르면 함수란 정의역의 하나의 원소가 하나의 공역 원소로 대응되어야 한다. 따라서, 만약 하나의 원소가 2개 이상의 공역 원소로 대응된다면 이는 함수가 아님을 의미한다. 정의에 의해 (a)와 (d)는 하나의 정의역 원소가 여러 개의 공역 원소와 대응되므로 함수가 아니다. 따라서, (b)와 (c) 그래프만 함수이다.
그래프 (b)의 정의역과 치역 : $D_{(b)} = [-2, 2], R_{(b)} = [-1, 2]$
그래프 (c)의 정의역과 치역 : $D_{(c)} = [-3, 2], R_{(c)} = [-3, -2) \cup [-1, 3]$
연습문제4. 함수 $f(x) = 3x^{2} - x + 2$일 때, $f(2), f(-2), f(a), f(a + 1)$을 구하여라.
1). $f(2) = 3 \cdot 2^{2} - 2 + 2 = 12$
2). $f(-2) = 3 \cdot (-2)^{2} - (-2) + 2 = 16$
3). $f(a) = 3a^{2} - a + 2 = 12$
4). $f(a + 1) = 3(a + 1)^{2} - (a + 1) + 2 = 3(a^{2} + 2a + 1) - a - 1 + 2 = 3a^{2} + 6a + 3 - a + 1 = 3a^{2} + 5a + 4$
연습문제5. 함수 $f(x) = \frac{x + 3}{x + 1}$일 때, $\frac{f(x) - f(1)}{x - 1}$을 구하여라.
$$\begin{align*} \frac{f(x) - f(1)}{x - 1} &= \frac{(x + 3)/(x + 1) - 2}{x - 1} \\ &= \frac{(x + 3) - 2(x + 1)}{(x - 1)(x + 1)} \\ &= \frac{-(x - 1)}{(x - 1)(x + 1)} \\ &= -\frac{1}{x + 1}\end{align*}$$
연습문제6. 함수 $f(x) = \frac{x}{3x - 1}, g(x) = \frac{5x + 4}{x^{2} + 3x + 2}, h(x) = \sqrt{x} + \sqrt{4 - x}$의 정의역을 구하여라.
1). $f(x) = \frac{x}{3x - 1}$
유리함수는 분모가 0이 되는 부분에서 정의되지 않기 때문에 함수 $f(x)$의 정의역은 $D_{f} = \{x \in \mathbb{R} | x \neq \frac{1}{3}\}$이다.
2). $g(x) = \frac{5x + 4}{x^{2} + 3x + 2}$
유리함수는 분모가 0이 되는 부분에서 정의되지 않기 때문에 함수 $g(x)$의 정의역은 $D_{g} = \{x \in \mathbb{R} | x \neq -1 \text{ and } x \neq -2\}$이다.
3). $h(x) = \sqrt{x} + \sqrt{4 - x}$
무리함수는 내부 값이 음수가 되는 부분에서 정의되지 않기 때문에 함수 $h(x)$의 정의역은 $D_{h} = \{x \in \mathbb{R} | 0 \le x \le 4\}$이다.
연습문제7. 함수 $f(x) = \frac{x}{x^{2} + 1}, g(x) = \frac{x^{2}}{x^{4} + 1}, h(x) = \frac{x}{x + 1}$를 우함수와 기함수로 구분하라.
1). $f(x) = \frac{x}{x^{2} + 1}$
$$\begin{align*} f(-x) &= \frac{-x}{(-x)^{2} + 1} \\ &= -\frac{x}{x^{2} + 1} = -f(x)\end{align*}$$
기함수의 정의에 의해 함수 $f(x)$는 기함수이다.
2). $g(x) = \frac{x^{2}}{x^{4} + 1}$
$$\begin{align*} g(-x) &= \frac{(-x)^{2}}{(-x)^{4} + 1} \\ &= -\frac{x^{2}}{x^{4} + 1} = g(x)\end{align*}$$
우함수의 정의에 의해 함수 $g(x)$는 우함수이다.
3). $h(x) = \frac{x}{x + 1}$
$$\begin{align*} h(-x) &= \frac{-x}{-x + 1} \\ &= \frac{x}{x - 1}\end{align*}$$
함수 $h(x)$는 우함수도 기함수도 아니다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.05.27 : 연습문제1 추가
22.06.09 : 연습문제2 - 7 추가
22.07.06 : 집합론 - 함수 링크 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 접선 (0) | 2021.08.16 |
|---|---|
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
| 미적분학 - 지수함수 (0) | 2021.08.14 |
| 미적분학 - 새로운 함수 만들기 (0) | 2021.08.11 |
| 미적분학 - 수학적 모델 (2) | 2021.08.10 |
안녕하세요. 이번 카테고리는 미적분학(Calculus)에 대해서 설명하고자 합니다. 미적분학은 물리학 현상(자유 낙하 운동, ...), 생물학(박테리아 증식 방정식, 생물 군집 특성 분석, ...), 사회학 등 많은 분야에서 활용되고 있어 사실 상 모든 대학교의 기본 과목으로 생각하시면 될 거 같습니다. 저 역시 수학과를 나왔기에 미적분학을 가장 먼저 수강하여 재밌게 들었던 기억이 있습니다. 하지만, 신입생 이후로 직접적으로 미적분학을 사용할 일이 없다가 대학원에 입학하니 미적분학에 대한 기초 개념이 필요하게 되었습니다. 그렇게 다시 공부를 하고자 이번 카테고리를 만들었으니 혹시 궁금하신 점이나 틀린 점이 있다면 지적 부탁드립니다.
오늘은 가장 처음이기 때문에 앞으로 배울 모든 내용의 주제가 되는 "함수(Function)"에 대해서 다루어보겠습니다. 사실 함수라는 하나의 주제만 해도 두꺼운 책을 쓸 수 있을 정도로 넓은 주제가 있습니다. 하지만 모든 범위를 다루기에는 제 지식도 얕을뿐만 아니라 흥미도 잃을 거 같아서 가벼운 주제만 정리하도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
1. 함수의 정의
정의1. 함수(Functions)
함수 $f$는 집합 $D$의 각 원소 $x$가 정확히 집합 $E$의 1개의 원소 $f(x)$에 대응되는 규칙이다.
설명
위와 같이 "함수 = 규칙"입니다. 여기서 몇 가지 용어를 정리하도록 하겠습니다.
- 정의역(Domain) $D = \text{dom}(f)$ : 함수 $f$의 모든 입력값의 집합
- 공역(Codomain) $E$ : 함수 $f$의 모든 가능한 출력값의 집합
- 치역(Range) $R \subseteq E$ : 함수 $f$의 정의역 $D$가 $f$에 의해 대응되는 모든 원소 $f(x)$의 집합
- 독립 변수(Independent variable) : 정의역 $D$의 임의의 원소
- 종속 변수(Dependent variable) : 치역 $R$의 임의의 원소
이 용어들은 모든 수학 분야에서 나오기 때문에 꼭 알아두어야 하는 개념입니다. 이를 그림으로 표현하면 아래와 같습니다.

예제1. $f(x) = 2x - 1, g(x) = x^{2}, h(x) = \sqrt{x}$의 정의역, 공역, 치역을 찾아라.
1). $f(x) = 2x - 1$를 그림으로 그려본다.

$f$의 정의역에는 특별한 조건이 없기 때문에 실수 전체 집합, 즉 $D = \mathbb{R}$이다. 공역 역시 모든 실수를 고려하기 때문에 $E = \mathbb{R}$이다. 마지막으로 치역은 함수 $f(x)$에 $D$의 모든 원소를 입력했을 때 모든 실수로 대응시킬 수 있기 때문에 $R = \mathbb{R}$이다.
$$D = E = R = \mathbb{R}$$
2). $g(x) = x^{2}$을 그림으로 그려본다.

$g$의 정의역에는 특별한 조건이 없기 때문에 실수 전체 집합, 즉 $D = \mathbb{R}$이다. 공역 역시 모든 실수를 고려하기 때문에 $E = \mathbb{R}$이다. 마지막으로 치역은 함수 $g(x)$에 $D$의 모든 원소를 입력했을 때 0을 포함하는 양의 실수로 대응시킬 수 있기 때문에 $R = \mathbb{R}_{+}$이다. 여기서 $\mathbb{R}_{+}$는 0이상의 모든 실수 집합을 의미한다.
$$D = E = \mathbb{R}, R = \mathbb{R}_{+}$$
3). $h(x) = \sqrt{x}$는 정의역의 조건이 루트 내의 실수는 항상 양수여야한다는 조건이 있기 때문에 $D = \mathbb{R}_{+}$이다. 그리고 기본적으로 공역은 모든 실수를 고려하기 때문에 $E = \mathbb{R}$이다. 마지막으로 치역은 $D$의 모든 원소를 입력했을 때 0을 포함하는 양의 실수로 대응시키기 때문에 $R = \mathbb{R}_{+}$이다.
$$D = R = \mathbb{R}_{+}, E = \mathbb{R}$$
또한 함수에는 위의 예시처럼 매끄럽게 1개의 함수로만 이루어진 경우도 있지만, 여러 개의 함수가 구간별로 정의된 경우도 있습니다. 이를 "조각함수(piecewise function)"라고 부릅니다. 가장 대표적인 조각 함수가 바로 절댓값 함수입니다.
$$f(x) = \left|x\right| = \begin{cases} x &x \ge 0 \\ -x &x < 0\end{cases}$$

절댓값 함수는 정의역이 양수라면 $x$, 음수라면 $-x$를 출력으로 뱉는 함수입니다. 이와 같이 특정 구간별로 다른 함수로 정의될 수 있습니다.
만약 함수에 대한 더욱 수학적인 내용이 궁금하시다면 집합론 - 함수를 참조해주시길 바랍니다.
2. 함수의 대칭성
다음으로 함수를 대칭성에 따라서 짝함수(even function), 기함수(odd function)으로 구분할 수 있습니다. 간단하게 짝함수는 $y$축에 대칭인 함수, 기함수는 원점 $(0, 0)$에 대칭인 함수를 의미합니다. 가장 대표적인 짝함수는 $f(x) = x^{2}$, 기함수는 $g(x) = x$입니다. 그리고 짝함수와 기함수를 판별하는 가장 쉬운 방법은 $x$ 대신에 $-x$를 넣어보는 것입니다. $f(-x) = f(x)$라면 $f(x)$는 짝함수, $f(-x) =-f(x)$이라면 $f(x)$는 기함수입니다. 예를 들어서 $f(-x) = (-x)^{2} = x^{2} = f(x)$이기 때문에 $f(x)$는 짝함수, $g(-x) = -x = -g(x)$이기 때문에 $g(x) = x$는 기함수입니다.
예제2.$f(x) = x^{5} + x, g(x) = 1 - x^{4}$가 짝함수인지, 기함수인지 판별하라
1). $f(-x) = (-x)^{5} + (-x) = -(x^{5} + x) = -f(x) \Rightarrow f(x)$는 기함수이다.
2). $g(-x) = 1 - (-x)^{4} = 1 - x^{4} = g(x) \Rightarrow g(x)$는 우함수이다.
3. 함수의 증감
정의2. 증가함수(increase function)와 감소함수(decrease function)
- 함수 $f$가 범위 $I$의 $x_{1} < x_{2}$를 만족하는 $x_{1}, x_{2}$에 대해서 $f(x_{1}) < f(x_{2})$가 성립하면 $f$는 증가함수이다.
- 함수 $f$가 범위 $I$의 $x_{1} < x_{2}$를 만족하는 $x_{1}, x_{2}$에 대해서 $f(x_{1}) > f(x_{2})$가 성립하면 $f$는 감소함수이다.
연습문제1. 아래와 같은 함수 그래프가 주어졌다고 할 때 물음에 답하여라.

(a). $f(-1)$의 값은 무엇인가?
(b). $f(x) = 2$일 때, $x$의 값은 무엇인가?
(c). $f$의 증가하는 구간은 어디인가?
(a). $f(-1) = -2$
(b). $f(x) = 2$일 때, $x = 1$과 $x = -3$
(c). $[-1, 3]$에서 함수 $f$는 증가한다.
연습문제2. 아래와 같은 함수 그래프가 주어졌다고 할 때 물음에 답하여라.

(a). $f(-4)$와 $g(3)$의 값은 무엇인가?
(b). $f(x) = g(x)$를 만족하는 $x$의 값은 무엇인가?
(c). $f$의 감소하는 구간은 어디인가?
(d). $f$와 $g$의 정의역과 치역은 어디인가?
(a). $f(-4) = -2, f(3) = 4$
(b). $x = \pm 2$
(c). $[0, 4]$
(d). 함수 $f$의 정의역과 치역 :$D_{f} = [-4, 4], R_{f} = [-2, 3]$
함수 $g$의 정의역과 치역 : $D_{g} = [-4, 3], R_{g} = [0.5, 4]$
연습문제3. 아래 4개의 그래프 중 함수인지 판별하고 함수라면 정의역과 치역을 구하여라.

정의1의 함수의 정의에 따르면 함수란 정의역의 하나의 원소가 하나의 공역 원소로 대응되어야 한다. 따라서, 만약 하나의 원소가 2개 이상의 공역 원소로 대응된다면 이는 함수가 아님을 의미한다. 정의에 의해 (a)와 (d)는 하나의 정의역 원소가 여러 개의 공역 원소와 대응되므로 함수가 아니다. 따라서, (b)와 (c) 그래프만 함수이다.
그래프 (b)의 정의역과 치역 : $D_{(b)} = [-2, 2], R_{(b)} = [-1, 2]$
그래프 (c)의 정의역과 치역 : $D_{(c)} = [-3, 2], R_{(c)} = [-3, -2) \cup [-1, 3]$
연습문제4. 함수 $f(x) = 3x^{2} - x + 2$일 때, $f(2), f(-2), f(a), f(a + 1)$을 구하여라.
1). $f(2) = 3 \cdot 2^{2} - 2 + 2 = 12$
2). $f(-2) = 3 \cdot (-2)^{2} - (-2) + 2 = 16$
3). $f(a) = 3a^{2} - a + 2 = 12$
4). $f(a + 1) = 3(a + 1)^{2} - (a + 1) + 2 = 3(a^{2} + 2a + 1) - a - 1 + 2 = 3a^{2} + 6a + 3 - a + 1 = 3a^{2} + 5a + 4$
연습문제5. 함수 $f(x) = \frac{x + 3}{x + 1}$일 때, $\frac{f(x) - f(1)}{x - 1}$을 구하여라.
$$\begin{align*} \frac{f(x) - f(1)}{x - 1} &= \frac{(x + 3)/(x + 1) - 2}{x - 1} \\ &= \frac{(x + 3) - 2(x + 1)}{(x - 1)(x + 1)} \\ &= \frac{-(x - 1)}{(x - 1)(x + 1)} \\ &= -\frac{1}{x + 1}\end{align*}$$
연습문제6. 함수 $f(x) = \frac{x}{3x - 1}, g(x) = \frac{5x + 4}{x^{2} + 3x + 2}, h(x) = \sqrt{x} + \sqrt{4 - x}$의 정의역을 구하여라.
1). $f(x) = \frac{x}{3x - 1}$
유리함수는 분모가 0이 되는 부분에서 정의되지 않기 때문에 함수 $f(x)$의 정의역은 $D_{f} = \{x \in \mathbb{R} | x \neq \frac{1}{3}\}$이다.
2). $g(x) = \frac{5x + 4}{x^{2} + 3x + 2}$
유리함수는 분모가 0이 되는 부분에서 정의되지 않기 때문에 함수 $g(x)$의 정의역은 $D_{g} = \{x \in \mathbb{R} | x \neq -1 \text{ and } x \neq -2\}$이다.
3). $h(x) = \sqrt{x} + \sqrt{4 - x}$
무리함수는 내부 값이 음수가 되는 부분에서 정의되지 않기 때문에 함수 $h(x)$의 정의역은 $D_{h} = \{x \in \mathbb{R} | 0 \le x \le 4\}$이다.
연습문제7. 함수 $f(x) = \frac{x}{x^{2} + 1}, g(x) = \frac{x^{2}}{x^{4} + 1}, h(x) = \frac{x}{x + 1}$를 우함수와 기함수로 구분하라.
1). $f(x) = \frac{x}{x^{2} + 1}$
$$\begin{align*} f(-x) &= \frac{-x}{(-x)^{2} + 1} \\ &= -\frac{x}{x^{2} + 1} = -f(x)\end{align*}$$
기함수의 정의에 의해 함수 $f(x)$는 기함수이다.
2). $g(x) = \frac{x^{2}}{x^{4} + 1}$
$$\begin{align*} g(-x) &= \frac{(-x)^{2}}{(-x)^{4} + 1} \\ &= -\frac{x^{2}}{x^{4} + 1} = g(x)\end{align*}$$
우함수의 정의에 의해 함수 $g(x)$는 우함수이다.
3). $h(x) = \frac{x}{x + 1}$
$$\begin{align*} h(-x) &= \frac{-x}{-x + 1} \\ &= \frac{x}{x - 1}\end{align*}$$
함수 $h(x)$는 우함수도 기함수도 아니다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.05.27 : 연습문제1 추가
22.06.09 : 연습문제2 - 7 추가
22.07.06 : 집합론 - 함수 링크 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 접선 (0) | 2021.08.16 |
|---|---|
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
| 미적분학 - 지수함수 (0) | 2021.08.14 |
| 미적분학 - 새로운 함수 만들기 (0) | 2021.08.11 |
| 미적분학 - 수학적 모델 (2) | 2021.08.10 |
