안녕하세요. 지난 포스팅의 미적분학 - 지수함수에서는 지수함수의 정의와 성질, 그리고 자연 상수를 밑으로한 지수함수의 특징에 대해서 알아보았습니다. 오늘은 역함수와 지수함수의 역함수의 로그함수, 역삼각함수에 대해서 간단히 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
1. 역함수(Inverse Function)
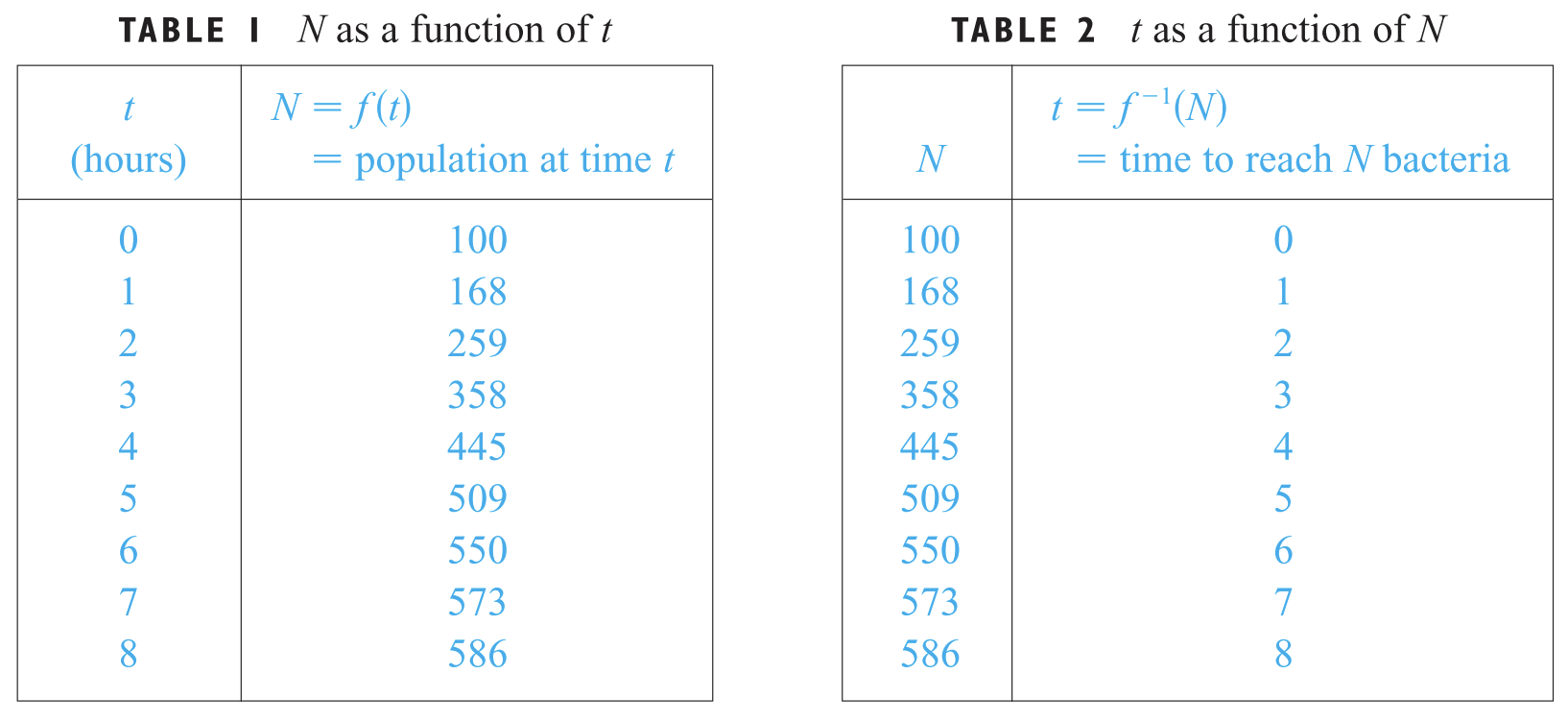
역함수를 설명하기 위해서 위의 표를 이용해보도록 하겠습니다. 왼쪽 표는 시간에 따른 박테리아 수를 나타낸 것입니다. $t = 0$일 때는 $f(0) = 100$마리의 박테리아가 있음을 의미합니다. 이제 궁금한 것은 만약 박테리아가 400마리 정도 있을 때 배양한지 몇 시간 째 지났는 지 알고 싶습니다. 이를 오른쪽 표를 통해서 보도록 하죠. 오른쪽 표는 박테리아 수에 따른 시간을 표현한 것 입니다. 예를 들어 박테리아가 550마리 정도 있다면 6시간 정도 지났다고 볼 수 있습니다. 두 표 사이의 차이점은 열이 뒤바뀐것 뿐입니다. 왼쪽 표는 시간을 기준으로, 오른쪽 표는 박테리아 수를 기준으로 표현하고 있습니다. 왼쪽 표를 $f(t) = N$이라고 했을 때, 오른쪽 표는 $f^{-1}(N) = t$라고 표현할 수 있습니다. 다시 돌아와서 저희가 400마리의 박테리아가 있을 때 어느 정도의 시간이 지났는 지 구하는 것은 $f^{-1}(400)$을 구하는 것과 동일합니다. 하지만 오른쪽 표에서는 $f^{-1}(400)$이 없기 때문에 $f^{-1}(358)$과 $f^{-1}(445)$의 평균을 고려하면 약 3시간 30분 정도 흘렀다는 것을 알 수 있습니다.
하지만, 모든 함수가 역함수를 가지고 있지 않습니다. 역함수를 가지기 위해서는 일대일 대응 함수(one-to-one function)이여야 합니다.
정의1. 일대일 대응 함수(one-to-one function)
함수 $f$가 모든 $x_{1} \neq x_{2}$를 만족하는 $x_{1}, x_{2}$에 대해서 $f(x_{1}) \neq f(x_{2})$를 만족한다면 함수 $f$를 일대일 대응 함수라고 한다.
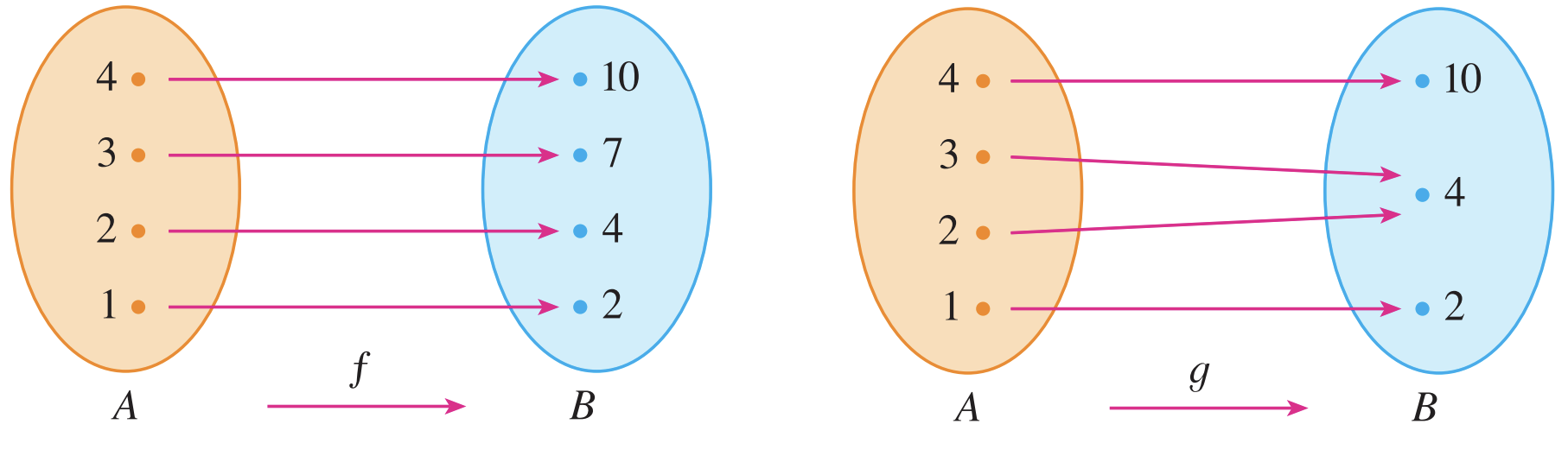
위의 그림에서 $f$는 일대일 대응 함수이고 $g$는 아닙니다. 왼쪽 그림은 모든 $A$의 원소가 $B$의 원소에 전부 다르게 대응됩니다. 하지만 오른쪽 그림에선느 $g(2) =g(3) = 4$이기 때문에 일대일 대응이 아닙니다.
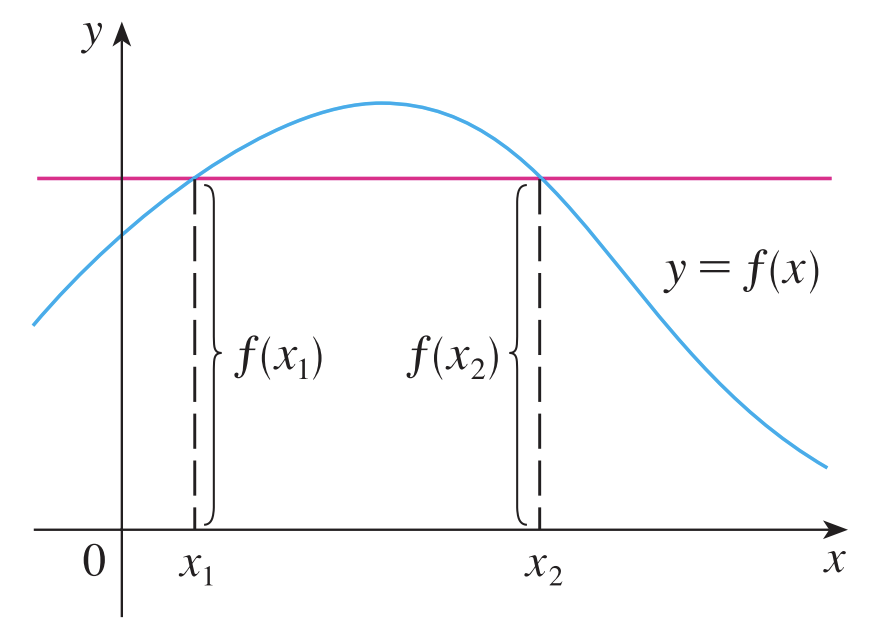
일대일 대응임을 가장 쉽게 판별할 수 있는 방법은 그래프를 그리는 것입니다. 예를 들어서 바로 위의 그림에서 수평선을 하나 쭉 그립니다. 그러면 1개의 $y$에 여러 개의 $x$가 대응되어 있다는 것을 알 수 있습니다. 이러한 판별 방식을 "수평선 검사(Horizontal Line Test)"라고 합니다.
예제1. $f(x) = x^{3}$가 일대일 대응 함수인지 확인하라
1). 정의를 통한 확인 : $x_{1} \neq x_{2}$라고 하자. $f(x)$는 증가함수이기 때문에 $x$ 값이 서로 다르면 함숫값이 같을 수 없기 때문에 $f(x_{1}) \neq f(x_{2})$이다.
2). 수평선 검사를 통한 확인
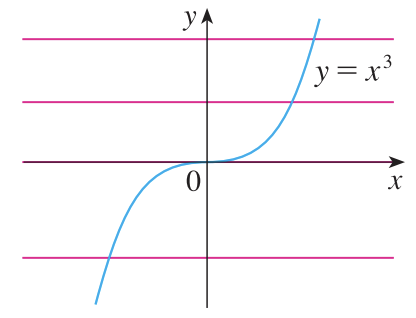
위의 그림에서 어떠한 $x$도 두 점에서 만나지 않기 때문에 $f(x)$는 일대일 대응 함수이다.
이와 같은 조건이 만족한다면 저희는 이제 역함수를 아래와 같이 정의할 수 있습니다.
정의2. 역함수(Inverse Function)
함수 $f$가 정의역 $A$에서 정의되고 치역 $B$와 일대일 대응이라고 하자. 그러면 $f$의 역함수 $f^{-1}$의 정의역은 $B$, 치역은 $A$이고 $f^{-1}(y) = x \Leftrightarrow f(x) = y$를 만족한다.
예를 들어서 $f(x) = x^{3}$의 역함수를 구해보도록 하겠습니다. 바로 예제1을 통해서 $f(x)$가 일대일 대응 함수임을 알았고, 정의역과 치역은 모두 $\mathbb{R}$입니다. 역함수를 구하는 가장 간단한 방법은 $x$와 $y$의 위치를 바꾸는 것 입니다. 따라서 저희는 $y = x^{3} \Leftrightarrow x = y^{3}$이기 때문에 $f^{-1}(x) = \sqrt[3]{x}$d임을 알 수 있습니다. 아주 간단하죠? 이때, 역함수 $f^{-1}(x)$의 정의역과 치역은 $f(x)$와 동일하게 $\mathbb{R}$입니다.
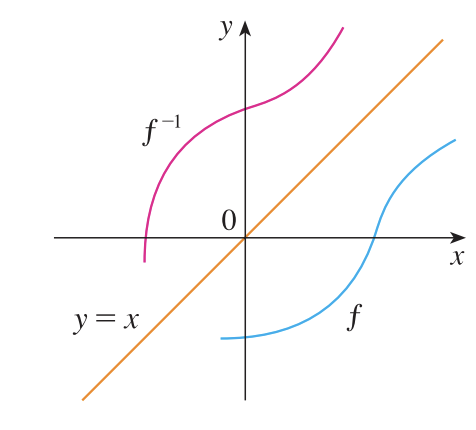
함수와 역함수를 그래프로 그렸을 때 나타나는 가장 큰 특징은 위의 그림과 같이 $y = x$ 대칭이라는 것입니다.
2. 로그함수(Logarithmic Function)
로그함수는 기본적으로 지수함수의 역함수입니다. 그렇다면 지수 함수도 일대일 대응 함수일까요? 맞습니다. 왜냐하면 애초에 지수함수 역시 증가함수이기 때문에 두 값이 다르면 함숫값이 다를 수 밖에 없기 때문이죠. 역함수를 정의하는 데는 문제가 없네요! 문제는 기호를 어떻게 정하는지 입니다. 보통 로그함수는 $\log_{a}(x)$라는 기호를 이용해서 표현합니다. $\log$는 로그함수를 의미하고 지수함수와 마찬가지로 밑 $a$에 따라서 모양이 달라집니다. 그래서 지수함수와 로그함수를 역함수 관계로 표현하면 아래와 같습니다.
$$\log_{a}(x) = y \Leftrightarrow a^{y} = x$$
로그함수 역시 지수함수와 마찬가지로 자주 쓰이는 성질 3가지가 있습니다.
- $\log_{a}(xy) = \log_{a}(x) + \log_{a}(y)$
- $\log_{a}\left(\frac{x}{y}\right) = \log_{a}(x) - \log_{a}(y)$
- $\log_{a}(x^{r}) = r\log(x)$
그리고 만약 밑이 자연 상수 $e$라면 특별히 자연로그라고 하며 기호로는 아래와 같이 표기합니다.
$$\log_{e}(x) = \ln(x)$$
또한 밑이 10이라면 보통 상용로그라고 합니다. 마지막으로 로그함수에서는 밑을 변환하는 공식으로 아래와 같이 씁니다.
$$\log_{a}(x) = \frac{\ln(x)}{\ln(a)}$$
3. 역삼각함수(Inverse Trigonometric Function)
역삼각함수도 로그함수와 크게 다르지 않고 그냥 삼각함수의 역함수를 의미합니다. 다만! 지수함수와는 다르게 삼각함수는 주기함수이기 때문에 일대일 대응함수가 아닙니다. 따라서 어느정도 $x$의 범위를 보정한 뒤 역함수를 구하는 과정이 필요합니다.

예를 들어 $\sin(x)$는 왼쪽과 같은 함수입니다. 그리고 수평선 검사를 해보면 1개의 함숫값에 대해서 무한 개의 값이 대응하게 됩니다. 이 상황에서는 역함수 자체를 정의할 수 없기 때문에 정의역의 범위를 $[-\frac{\pi}{2}, \frac{\pi}{2}]$로 제한합니다. 그러면 오른쪽 그림과 같이 일대일 대응 함수가 만들어지게 됩니다. 이를 기호로 표현하면 $\arcsin(x) = \sin^{-1}(x)$가 됩니다. 이와 유사한 방법으로 $\cos(x)$는 $[0, \pi]$, $\tan(x)$는 $[-1, 1]$까지 정의역을 제한하면 역함수 $\arccos(x) = \cos^{-1}(x)$와 $\arctan(x) = \tan^{-1}(x)$를 얻을 수 있습니다.
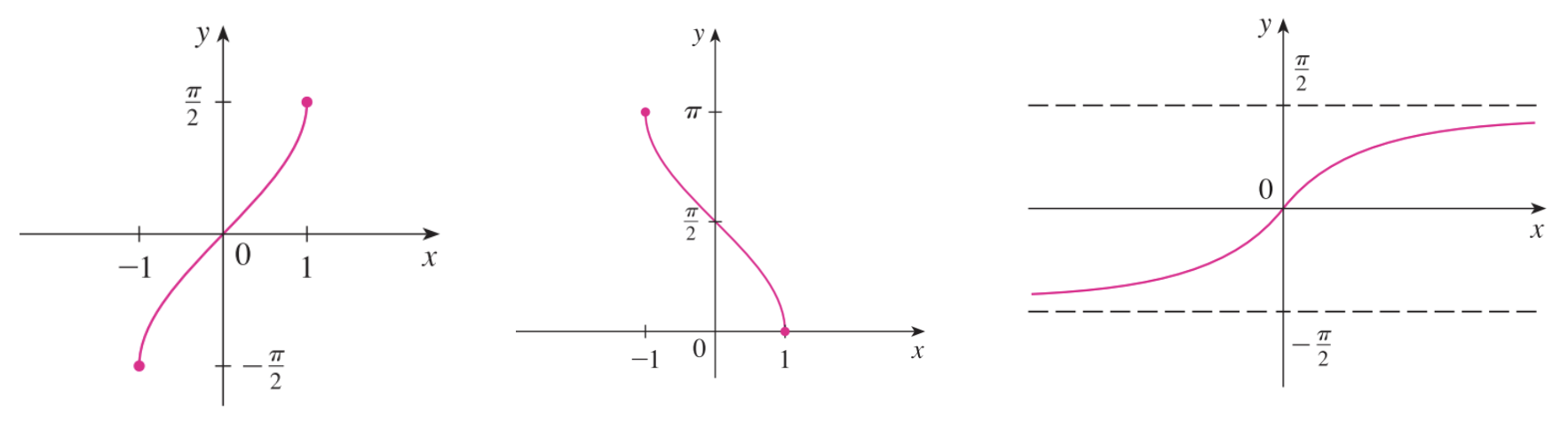
위 그림은 오른쪽부터 $\arcsin(x), \arccos(x), \arctan(x)$ 함수를 의미합니다. 기존의 함수와 정확히 $y = x$ 대칭임을 확인할 수 있습니다.
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 함수의 극한 (0) | 2021.08.17 |
|---|---|
| 미적분학 - 접선 (0) | 2021.08.16 |
| 미적분학 - 지수함수 (0) | 2021.08.14 |
| 미적분학 - 새로운 함수 만들기 (0) | 2021.08.11 |
| 미적분학 - 수학적 모델 (2) | 2021.08.10 |
안녕하세요. 지난 포스팅의 미적분학 - 지수함수에서는 지수함수의 정의와 성질, 그리고 자연 상수를 밑으로한 지수함수의 특징에 대해서 알아보았습니다. 오늘은 역함수와 지수함수의 역함수의 로그함수, 역삼각함수에 대해서 간단히 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
1. 역함수(Inverse Function)

역함수를 설명하기 위해서 위의 표를 이용해보도록 하겠습니다. 왼쪽 표는 시간에 따른 박테리아 수를 나타낸 것입니다. t=0일 때는 f(0)=100마리의 박테리아가 있음을 의미합니다. 이제 궁금한 것은 만약 박테리아가 400마리 정도 있을 때 배양한지 몇 시간 째 지났는 지 알고 싶습니다. 이를 오른쪽 표를 통해서 보도록 하죠. 오른쪽 표는 박테리아 수에 따른 시간을 표현한 것 입니다. 예를 들어 박테리아가 550마리 정도 있다면 6시간 정도 지났다고 볼 수 있습니다. 두 표 사이의 차이점은 열이 뒤바뀐것 뿐입니다. 왼쪽 표는 시간을 기준으로, 오른쪽 표는 박테리아 수를 기준으로 표현하고 있습니다. 왼쪽 표를 f(t)=N이라고 했을 때, 오른쪽 표는 f−1(N)=t라고 표현할 수 있습니다. 다시 돌아와서 저희가 400마리의 박테리아가 있을 때 어느 정도의 시간이 지났는 지 구하는 것은 f−1(400)을 구하는 것과 동일합니다. 하지만 오른쪽 표에서는 f−1(400)이 없기 때문에 f−1(358)과 f−1(445)의 평균을 고려하면 약 3시간 30분 정도 흘렀다는 것을 알 수 있습니다.
하지만, 모든 함수가 역함수를 가지고 있지 않습니다. 역함수를 가지기 위해서는 일대일 대응 함수(one-to-one function)이여야 합니다.
정의1. 일대일 대응 함수(one-to-one function)
함수 f가 모든 x1≠x2를 만족하는 x1,x2에 대해서 f(x1)≠f(x2)를 만족한다면 함수 f를 일대일 대응 함수라고 한다.

위의 그림에서 f는 일대일 대응 함수이고 g는 아닙니다. 왼쪽 그림은 모든 A의 원소가 B의 원소에 전부 다르게 대응됩니다. 하지만 오른쪽 그림에선느 g(2)=g(3)=4이기 때문에 일대일 대응이 아닙니다.

일대일 대응임을 가장 쉽게 판별할 수 있는 방법은 그래프를 그리는 것입니다. 예를 들어서 바로 위의 그림에서 수평선을 하나 쭉 그립니다. 그러면 1개의 y에 여러 개의 x가 대응되어 있다는 것을 알 수 있습니다. 이러한 판별 방식을 "수평선 검사(Horizontal Line Test)"라고 합니다.
예제1. f(x)=x3가 일대일 대응 함수인지 확인하라
1). 정의를 통한 확인 : x1≠x2라고 하자. f(x)는 증가함수이기 때문에 x 값이 서로 다르면 함숫값이 같을 수 없기 때문에 f(x1)≠f(x2)이다.
2). 수평선 검사를 통한 확인

위의 그림에서 어떠한 x도 두 점에서 만나지 않기 때문에 f(x)는 일대일 대응 함수이다.
이와 같은 조건이 만족한다면 저희는 이제 역함수를 아래와 같이 정의할 수 있습니다.
정의2. 역함수(Inverse Function)
함수 f가 정의역 A에서 정의되고 치역 B와 일대일 대응이라고 하자. 그러면 f의 역함수 f−1의 정의역은 B, 치역은 A이고 f−1(y)=x⇔f(x)=y를 만족한다.
예를 들어서 f(x)=x3의 역함수를 구해보도록 하겠습니다. 바로 예제1을 통해서 f(x)가 일대일 대응 함수임을 알았고, 정의역과 치역은 모두 R입니다. 역함수를 구하는 가장 간단한 방법은 x와 y의 위치를 바꾸는 것 입니다. 따라서 저희는 y=x3⇔x=y3이기 때문에 f−1(x)=3√xd임을 알 수 있습니다. 아주 간단하죠? 이때, 역함수 f−1(x)의 정의역과 치역은 f(x)와 동일하게 R입니다.
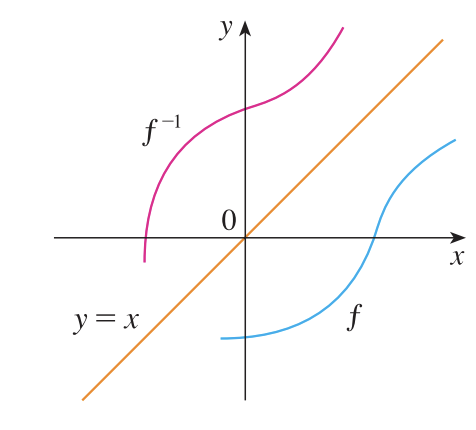
함수와 역함수를 그래프로 그렸을 때 나타나는 가장 큰 특징은 위의 그림과 같이 y=x 대칭이라는 것입니다.
2. 로그함수(Logarithmic Function)
로그함수는 기본적으로 지수함수의 역함수입니다. 그렇다면 지수 함수도 일대일 대응 함수일까요? 맞습니다. 왜냐하면 애초에 지수함수 역시 증가함수이기 때문에 두 값이 다르면 함숫값이 다를 수 밖에 없기 때문이죠. 역함수를 정의하는 데는 문제가 없네요! 문제는 기호를 어떻게 정하는지 입니다. 보통 로그함수는 loga(x)라는 기호를 이용해서 표현합니다. log는 로그함수를 의미하고 지수함수와 마찬가지로 밑 a에 따라서 모양이 달라집니다. 그래서 지수함수와 로그함수를 역함수 관계로 표현하면 아래와 같습니다.
loga(x)=y⇔ay=x
로그함수 역시 지수함수와 마찬가지로 자주 쓰이는 성질 3가지가 있습니다.
- loga(xy)=loga(x)+loga(y)
- loga(xy)=loga(x)−loga(y)
- loga(xr)=rlog(x)
그리고 만약 밑이 자연 상수 e라면 특별히 자연로그라고 하며 기호로는 아래와 같이 표기합니다.
loge(x)=ln(x)
또한 밑이 10이라면 보통 상용로그라고 합니다. 마지막으로 로그함수에서는 밑을 변환하는 공식으로 아래와 같이 씁니다.
loga(x)=ln(x)ln(a)
3. 역삼각함수(Inverse Trigonometric Function)
역삼각함수도 로그함수와 크게 다르지 않고 그냥 삼각함수의 역함수를 의미합니다. 다만! 지수함수와는 다르게 삼각함수는 주기함수이기 때문에 일대일 대응함수가 아닙니다. 따라서 어느정도 x의 범위를 보정한 뒤 역함수를 구하는 과정이 필요합니다.

예를 들어 sin(x)는 왼쪽과 같은 함수입니다. 그리고 수평선 검사를 해보면 1개의 함숫값에 대해서 무한 개의 값이 대응하게 됩니다. 이 상황에서는 역함수 자체를 정의할 수 없기 때문에 정의역의 범위를 [−π2,π2]로 제한합니다. 그러면 오른쪽 그림과 같이 일대일 대응 함수가 만들어지게 됩니다. 이를 기호로 표현하면 arcsin(x)=sin−1(x)가 됩니다. 이와 유사한 방법으로 cos(x)는 [0,π], tan(x)는 [−1,1]까지 정의역을 제한하면 역함수 arccos(x)=cos−1(x)와 arctan(x)=tan−1(x)를 얻을 수 있습니다.

위 그림은 오른쪽부터 arcsin(x),arccos(x),arctan(x) 함수를 의미합니다. 기존의 함수와 정확히 y=x 대칭임을 확인할 수 있습니다.
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 함수의 극한 (0) | 2021.08.17 |
|---|---|
| 미적분학 - 접선 (0) | 2021.08.16 |
| 미적분학 - 지수함수 (0) | 2021.08.14 |
| 미적분학 - 새로운 함수 만들기 (0) | 2021.08.11 |
| 미적분학 - 수학적 모델 (2) | 2021.08.10 |
