안녕하세요. 지난 포스팅의 미적분학 - 접선에서는 어떤 점에서 곡선의 접선을 찾는 근사적인 방법에 대해서 알아보았습니다. 오늘은 이를 명확하게 정의하기 위해서 함수의 극한에 대해서 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.

사실 그림으로 보면 쉽게 이해가실 겁니다. 예를 들어 위의 그림을 보도록 하죠. $y = f(x) = x^{2} - x + 2$라는 그래프가 있습니다. 그리고 $x = 2$를 기준으로 왼쪽, 오른쪽에서 천천히 접근한다고 가정하겠습니다. 그러면 오른쪽 표와 같이 $f(x)$는 $x < 2$일 때는 4보다는 작지면 점점 4에 가까워지고 있습니다. 그와 반면에 $x > 2$일 때는 4보다는 크지만 점점 가까워지고 있죠. 그리고 $x$가 2로 더 가까워지면 언젠가는 $f(x) = 4$가 될 것 입니다. 이를 수학적으로 표현하면 아래와 같죠.
$$\lim_{x \rightarrow 2} (x^{2} - x + 2) = 4$$
따라서, 함수의 극한이라는 것은 어떤 함수 $f(x)$가 있을 때 어떤 값 $x = a$에 무한히 가까워질 때의 값을 구하는 것임을 알 수 있습니다. 이를 더욱 명확하게 $\epsilon - \delta$ 논법을 이용해서 정의할 수도 있지만 저희는 여기에서 잠시 멈추도록 하죠. 여기까지만 이해해도 이후에 미적분학을 공부하는 데는 큰 지장은 없습니다.(다만, 수학과 전공생들은 아니겠죠 ㅠㅠ) 다만 저희는 앞으로 함수의 극한을 쓸 때 아래와 같이 쓰도록 하겠습니다.
$$\lim_{x \rightarrow a} f(x) = L$$
여기서 $\lim$은 극한을 취한다는 것을 의미합니다. 그리고 $x \rightarrow a$는 극한을 어디로 취할지를 명시하고 $f(x)$는 극한을 취할 함수가 됩니다. 마지막으로 $L$은 함수 $f(x)$가 $x = a$로 무한히 접근했을 때 얻을 수 있는 극한값이 됩니다. 지금까지 함수 극한의 정의에 대해서 간략하게 보았습니다. 그렇다면,
함수의 극한값은 항상 존재하는가?
즉, 저희는 이제부터 극한값의 존재성에 대해서 생각해볼 차례입니다. 답은 당연히 항상 존재하지 않습니다. 함수의 극한값이 존재할 수 있는 조건을 고려해보도록 하겠습니다. 저희가 처음에 극한값을 계산할 때 어떻게 했는 지 상기해보면 $x = a$를 기준으로 왼쪽에서 접근하는 극한, 그리고 오른쪽에서 접근하는 극한으로 고려했습니다. 이를 각각 좌극한, 우극한이라고 합니다. $y = f(x) = x^{2} - x + 2$같은 경우에는 좌극한과 우극한의 값이 동일했기 때문에 무난하게 쓸 수 있었습니다. 이제부터 저희는 좌극한과 우극한을 각각 $\lim_{x \rightarrow a^{-}} f(x)$와 $\lim_{x \rightarrow a^{+}} f(x)$로 작성하도록 하겠습니다. 다들 예상하셨다싶이 극한값이 존재하기 위해서는 좌극한과 우극한이 동일해야 합니다.
$$\lim_{x \rightarrow a} f(x) = L \text{ if and only if } \lim_{x \rightarrow a^{-}} f(x) = \lim_{x \rightarrow a^{+}} f(x) = L$$
앞으로 자주 보겠지만 $\text{if and only if}$는 "필요충분조건"을 의미합니다.
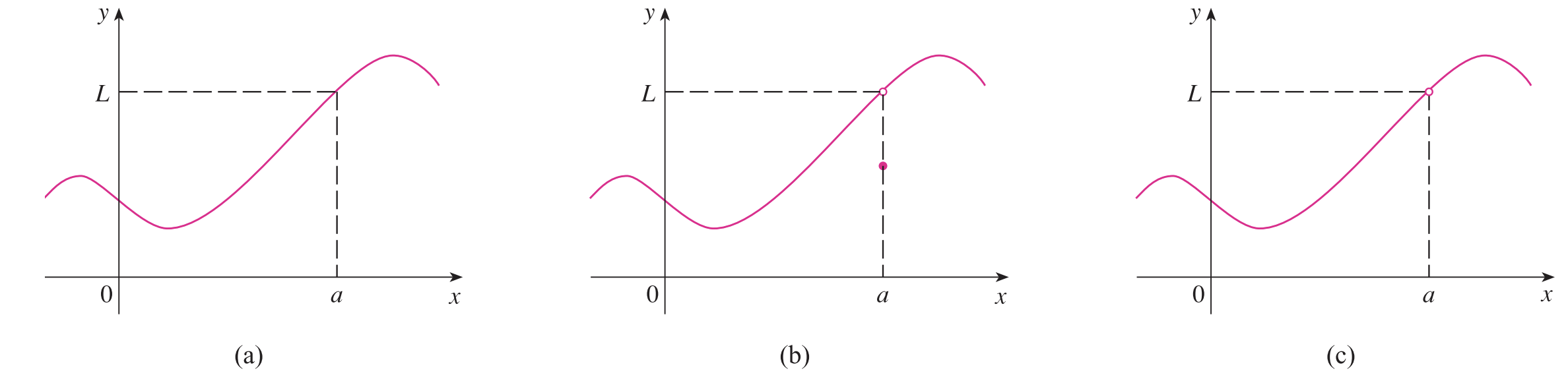
위의 그림에서 $x = a$에서의 극한값이 존재하는 그림은 무엇일까요? 하나씩 보도록 하겠습니다. (a)는 좌극한, 우극한이 동일하네요? 그러니까 극한값이 존재합니다. (b)는 (a)와 조금 다릅니다. $f(a) \neq L$입니다. 하지만 여전히 극한값은 존재합니다. (c)는 어떨까요? 이번에는 아예 $f(a)$가 정의되지 않습니다. 그럼에도 불구하고 극한값은 존재합니다. 이를 통해서 알 수 있는 것은 함숫값과 극한값의 존재성과 관련이 없다는 것입니다. 따라서 극한값이 존재한다는 것은 생각보다 넓은 범위의 조건이라고 볼 수 있겠네요.(참고로 극한값 = 함숫값인 경우에는 저희가 잘 아는 "연속 함수"라고 부릅니다.)
여기서 절대 헷갈리시면 안되는 것이 있습니다. 극한값이 존재하지 않는 것과 극한값이 무한대($\infty, -\infty$)라는 것은 다릅니다. 존재하지 않는다는 것은 좌극한,우극한이 서로 다를 때고 무한대일 때는 좌극한, 우극한이 모두 무한대를 향하고 있기 때문입니다.
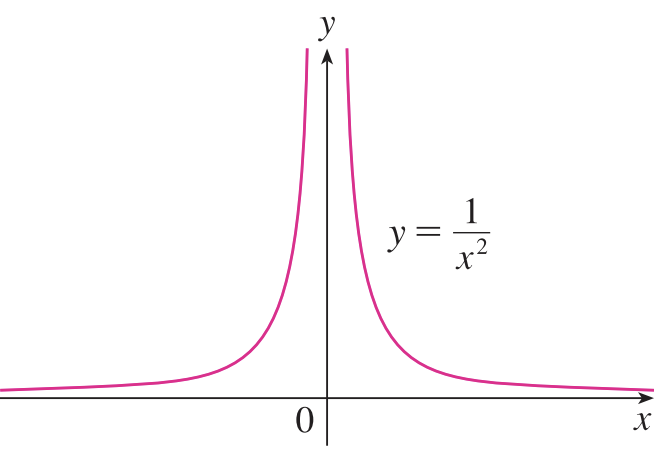
예를 들어서 위의 그림에서 $x = 0$에서의 극한값은 $\infty$입니다. 즉, $\lim_{x \rightarrow 0} \frac{1}{x^{2}} = \infty$이죠. 이는 극한값이 존재한다고 표현은 합니다.
연습문제1. 함수 $f$가 아래의 그래프로 주어진다고 할 때 아래의 식의 결과를 각각 구하여라.
1). $\lim_{x \rightarrow 0} f(x)$
2). $\lim_{x \rightarrow 3^{-}} f(x)$
3). $\lim_{x \rightarrow 3^{+}} f(x)$
4). $\lim_{x \rightarrow 3} f(x)$
5). $f(3)$

1). $\lim_{x \rightarrow 0} f(x) = 3$
2). $\lim_{x \rightarrow 3^{-}} f(x) = 4$
3). $\lim_{x \rightarrow 3^{+}} f(x) = 2$
4). $\lim_{x \rightarrow 3} f(x)$은 좌극한과 우극한의 값이 서로 일치하지 않기 때문에 정의되지 않는다.
5). $f(3) = 3$
연습문제2. 함수 $f$가 아래의 그래프로 주어진다고 할 때 아래의 식의 결과를 각각 구하여라.
1). $\lim_{x \rightarrow 1^{-}} f(x)$
2). $\lim_{x \rightarrow 1^{+}} f(x)$
3). $\lim_{x \rightarrow 1} f(x)$
4). $\lim_{x \rightarrow 5} f(x)$
5). $f(5)$

1). $\lim_{x \rightarrow 1^{-}} f(x) = 2$
2). $\lim_{x \rightarrow 1^{+}} f(x) = 3$
3). $\lim_{x \rightarrow 1} f(x)$은 좌극한과 우극한의 값이 서로 일치하지 않기 때문에 정의되지 않는다.
4). $\lim_{x \rightarrow 5} f(x)$ = 4
5). $f(5)$ : $x = 5$은 정의역에 포함되어 있지 않은 영역이기 때문에 함수값이 정의되지 않는다.
연습문제3. 함수 $f$가 아래의 그래프로 주어진다고 할 때 아래의 식의 결과를 각각 구하여라.
1). $\lim_{x \rightarrow -3^{-}} f(x)$
2). $\lim_{x \rightarrow -3^{+}} f(x)$
3). $\lim_{x \rightarrow -3} f(x)$
4). $f(-3)$
5). $\lim_{x \rightarrow 0^{-}} f(x)$
6). $\lim_{x \rightarrow 0^{+}} f(x)$
7). $\lim_{x \rightarrow 0} f(x)$
8). $f(0)$
9). $\lim_{x \rightarrow 2} f(x)$
10). $f(2)$
11). $\lim_{x \rightarrow 5^{+}}$
12). $\lim_{x \rightarrow 5^{-}} f(x)$

1). $\lim_{x \rightarrow -3^{-}} f(x) = 4$
2). $\lim_{x \rightarrow -3^{+}} f(x) = 4$
3). $\lim_{x \rightarrow -3} f(x) = 4$
4). $f(-3)$ : $x = -3$은 정의역에 포함되어 있지 않은 영역이기 때문에 함수값이 정의되지 않는다.
5). $\lim_{x \rightarrow 0^{-}} f(x) = 1$
6). $\lim_{x \rightarrow 0^{+}} f(x) = -1$
7). $\lim_{x \rightarrow 0} f(x)$은 좌극한과 우극한의 값이 서로 일치하지 않기 때문에 정의되지 않는다.
8). $f(0) = 1$
9). $\lim_{x \rightarrow 2} f(x) = 2$
10). $f(2)$ : $x = 2$은 정의역에 포함되어 있지 않은 영역이기 때문에 함수값이 정의되지 않는다.
11). $\lim_{x \rightarrow 5^{+}} = 3$
12). $\lim_{x \rightarrow 5^{-}} f(x)$ : $x < 5$인 일 때 함수 $f(x)$는 2와 4 사이를 크게 진동하며 감소를 하지 않기 때문에 수렴하지 않고 진동한다.
연습문제4. 함수 $f$가 아래의 그래프로 주어진다고 할 때 아래의 식의 결과를 각각 구하여라.
1). $\lim_{x \rightarrow 0^{-}} f(x)$
2). $\lim_{x \rightarrow 0^{+}} f(x)$
3). $\lim_{x \rightarrow 0} f(x)$
4). $\lim_{x \rightarrow 2^{-}} f(x)$
5). $\lim_{x \rightarrow 2^{+}} f(x)$
6). $\lim_{x \rightarrow 2} f(x)$
7). $f(2)$
8). $\lim_{x \rightarrow 4} f(x)$

1). $\lim_{x \rightarrow 0^{-}} f(x) = -1$
2). $\lim_{x \rightarrow 0^{+}} f(x) = -2$
3). $\lim_{x \rightarrow 0} f(x)$은 좌극한과 우극한의 값이 서로 일치하지 않기 때문에 정의되지 않는다.
4). $\lim_{x \rightarrow 2^{-}} f(x) = 2$
5). $\lim_{x \rightarrow 2^{+}} f(x) = 0$
6). $\lim_{x \rightarrow 2} f(x)$은 좌극한과 우극한의 값이 서로 일치하지 않기 때문에 정의되지 않는다.
7). $f(2) = 1$
8). $\lim_{x \rightarrow 4} f(x) = 3$
연습문제5. 함수 $f$가 아래의 그래프로 주어진다고 할 때 아래의 식의 결과를 각각 구하여라.
1). $\lim_{x \rightarrow 2} f(x)$
2). $\lim_{x \rightarrow 5} f(x)$
3). $\lim_{x \rightarrow 3^{-}} f(x)$
4). $\lim_{x \rightarrow 3^{+}} f(x)$
5). 함수 $f(x)$의 수직점근선을 구하여라.

1). $\lim_{x \rightarrow 2} f(x) = -\infty$
2). $\lim_{x \rightarrow 5} f(x) = \infty$
3). $\lim_{x \rightarrow 3^{-}} f(x) = -\infty$
4). $\lim_{x \rightarrow 3^{+}} f(x) = \infty$
5). $x = -3$ 그리고 $x = 5$
연습문제6. 함수 $f$가 아래의 그래프로 주어진다고 할 때 아래의 식의 결과를 각각 구하여라.
1). $\lim_{x \rightarrow -7} f(x)$
2). $\lim_{x \rightarrow -3} f(x)$
3). $\lim_{x \rightarrow 0} f(x)$
4). $\lim_{x \rightarrow 6^{-}} f(x)$
5). $\lim_{x \rightarrow 6^{+}} f(x)$
6). 함수 $f(x)$의 수직점근선을 구하여라.

1). $\lim_{x \rightarrow -7} f(x) = -\infty$
2). $\lim_{x \rightarrow -3} f(x) = \infty$
3). $\lim_{x \rightarrow 0} f(x) = \infty$
4). $\lim_{x \rightarrow 6^{-}} f(x) = -\infty$
5). $\lim_{x \rightarrow 6^{+}} f(x) = \infty$
6). $x = -7, x = 3, x = 0$ 그리고 $x = 6$
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.07.01 : 연습문제1-6 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 정확한 극한의 정의 (0) | 2021.08.25 |
|---|---|
| 미적분학 - 극한 법칙을 이용한 극한 계산하기 (0) | 2021.08.20 |
| 미적분학 - 접선 (0) | 2021.08.16 |
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
| 미적분학 - 지수함수 (0) | 2021.08.14 |
