안녕하세요. 지난 포스팅의 미적분학 - 함수의 극한에서는 극한을 간단하게 정의하고 계산해보았습니다. 오늘은 극한 법칙과 이를 활용한 극한 계산법에 대해서 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
일단 $\lim_{x \rightarrow a}f(x)$와 $\lim_{x \rightarrow a} g(x)$가 존재한다고 가정하겠습니다. 그러면 아래의 법칙들이 성립합니다.
- $\lim_{x \rightarrow a} \left[f(x) \pm g(x)\right] = \lim_{x \rightarrow a} f(x) \pm \lim_{x \rightarrow a} g(x)$
- $\lim_{x \rightarrow a} \left[cf(x)\right] = c\lim_{x \rightarrow} f(x)$
- $\lim_{x \rightarrow a} \left[f(x) g(x)\right] = \left[\lim_{x \rightarrow a}f(x)\right]\left[\lim_{x \rightarrow a} g(x)\right]$
- $\lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \frac{\lim_{x \rightarrow a} f(x)}{\lim_{x \rightarrow a} g(x)}$(이때, $\lim_{x \rightarrow g(x)} \neq 0$ 이여야 합니다!)
- $\lim_{x \rightarrow a} \left[f(x)\right]^{n} = \left[\lim_{x \rightarrow a} f(x)\right]^{n}$
- $\lim_{x \rightarrow a} c = c$
- $\lim_{x \rightarrow a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \rightarrow a} f(x)}$
예제1.$\lim_{x \rightarrow 2} f(x) = 4, \lim_{x \rightarrow 2} g(x) = -2, \lim_{x \rightarrow 2} h(x) = 0$이라고 할 때 아래의 식을 계산하시오.
- $\lim_{x \rightarrow 2} \left[f(x) + 5g(x)\right]$
- $\lim_{x \rightarrow 2} \frac{3f(x)}{g(x)}$
- $\lim_{x \rightarrow 2} \frac{g(x)}{h(x)}$
1. $$\begin{align} \lim_{x \rightarrow 2} \left[f(x) + 5g(x)\right] &= \lim_{x \rightarrow 2} f(x) + \lim_{x \rightarrow 2 } 5g(x) \\ &= \lim_{x \rightarrow 2} f(x) + 5\lim_{x \rightarrow 2} g(x) \\ &= 4 + 5 \cdot (-2) = -6\end{align}$$
2. $$\begin{align} \lim_{x \rightarrow 2} \frac{3f(x)}{g(x)}&= \frac{\lim_{x \rightarrow 2} 3f(x)}{\lim_{x \rightarrow 2}g(x)} \\ &= \frac{3\lim_{x \rightarrow 2} f(x)}{\lim_{x \rightarrow 2}g(x)} \\ &= \frac{3 \cdot 4}{-2} = -6\end{align}$$
3. $\lim_{x \rightarrow 2} h(x) = 0$이기 때문에 극한은 정의되지 않는다.
예제2.$\lim_{x \rightarrow 2} \frac{\sqrt{6 - x} - 2}{\sqrt{3 - x} - 1}$을 계산하라.
$$\begin{align} \lim_{x \rightarrow 2} \frac{\sqrt{6 - x} - 2}{\sqrt{3 - x} - 1} &= \lim_{x \rightarrow 2} \frac{\left(\sqrt{6 - x} - 2\right)\left(\sqrt{3 - x} + 1\right)}{\left(\sqrt{3 - x} - 1\right)\left(\sqrt{3 - x} + 1\right)} \\ &= \lim_{x \rightarrow 2} \frac{(\sqrt{6 - x} - 2)(\sqrt{3 - x} + 1)}{2 - x} \\ &= \lim_{x \rightarrow 2} \frac{(\sqrt{6 - x} - 2)}{2 - x} \cdot (\sqrt{3 - x} + 1) \\ &= \lim_{x \rightarrow 2} \frac{\sqrt{6 - x} - 2}{2 - x} \lim_{x \rightarrow 2} (\sqrt{3 - x} + 1) \\ &= 2\lim_{x \rightarrow 2} \frac{\sqrt{6 - x} - 2}{2 - x} \\ &= 2\lim_{x \rightarrow 2} \frac{(\sqrt{6 - x} - 2)(\sqrt{6 - x} + 2)}{(2 - x)(\sqrt{6 - x} + 2)} \\ &= 2\lim_{x \rightarrow 2} \frac{2 - x}{(2 - x)(\sqrt{6 - x} + 2)} \\ &= 2 \lim_{x \rightarrow 2} \frac{1}{\sqrt{6 - x} + 2} = \frac{2}{4} = \frac{1}{2}\end{align}$$
또한 만약 두 함수 사이의 대소 관계가 명확하면 아래의 법칙들도 성립합니다. $f(x) \le h(x) \le g(x)$라고 가정하겠습니다.
- $\lim_{x \rightarrow a} f(x) \le \lim_{x \rightarrow a} g(x)$
- $\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a} g(x) = L \Rightarrow \lim_{x \rightarrow a} h(x) = L$
연습문제1. 각 함수 $f, g, h$에 대해서 $\lim_{x \rightarrow 2} f(x) = 4, \lim_{x \rightarrow 2} g(x) = -2, \lim_{x \rightarrow 2} h(x) = 0$이 성립한다고 가정했을 때 아래의 식들을 구하여라.
1). $\lim_{x \rightarrow 2} \left[f(x)+ 5g(x)\right]$
2). $\lim_{x \rightarrow 2} \left[g(x)\right]^{3}$
3). $\lim_{x \rightarrow 2} \sqrt{f(x)}$
4). $\lim_{x \rightarrow 2} \frac{3f(x)}{g(x)}$
5). $\lim_{x \rightarrow 2} \frac{g(x)}{h(x)}$
6). $\lim_{x \rightarrow 2} \frac{g(x)h(x)}{f(x)}$
1). $\lim_{x \rightarrow 2} \left[f(x)+ 5g(x)\right] = \lim_{x \rightarrow 2} f(x) +5\lim_{x \rightarrow 2} g(x) = 4 + 5 \cdot (-2) = -6$
2). $\lim_{x \rightarrow 2} \left[g(x)\right]^{3} = \left[\lim_{x \rightarrow 2} g(x)\right]^{3} = (-2)^{3} = -8$
3). $\lim_{x \rightarrow 2} \sqrt{f(x)} = \sqrt{\lim_{x \rightarrow 2} f(x)} = \sqrt{4} = 2$
4). $\lim_{x \rightarrow 2} \frac{3f(x)}{g(x)} = \frac{3\lim_{x \rightarrow 2} f(x)}{\lim_{x \rightarrow 2} g(x)} = -6$
5). $\lim_{x \rightarrow 2} \frac{g(x)}{h(x)}$ : $\lim_{x \rightarrow 2} h(x) = 0$이기 때문에 정의되지 않는다.
6). $\lim_{x \rightarrow 2} \frac{g(x)h(x)}{f(x)} = \frac{\left[\lim_{x \rightarrow 2} g(x) \right] \left[\lim_{x \rightarrow 2} h(x)\right]}{\lim_{x \rightarrow 2} f(x)} = \frac{(-2) \cdot 0}{4}=0$
연습문제2. 각 함수 $f$와 $g$가 아래의 그래프로 주어져있을 때 아래의 식들을 구하여라.
1). $\lim_{x \rightarrow 2} \left[f(x) + g(x)\right]$
2). $\lim_{x \rightarrow 1} \left[f(x) + g(x)\right]$
3). $\lim_{x \rightarrow 0} \left[f(x)g(x)\right]$
4). $\lim_{x \rightarrow -1} \frac{f(x)}{g(x)}$
5). $\lim_{x \rightarrow 2} \left[x^{3}f(x)\right]$
6). $\lim_{x \rightarrow 1} \sqrt{3 + f(x)}$
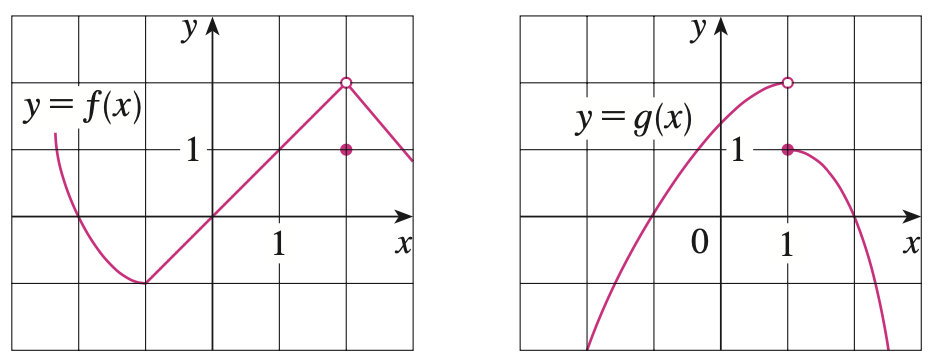
1). $\lim_{x \rightarrow 2} \left[f(x) + g(x)\right] = \lim_{x \rightarrow 2} f(x) + \lim_{x \rightarrow 2} g(x) = 2 + 0 = 2$
2). $\lim_{x \rightarrow 1} \left[f(x) + g(x)\right] : $\lim_{x \rightarrow 1} g(x)$의 좌극한과 우극한이 달라 극한값이 정의되지 않는다.
3). $\lim_{x \rightarrow 0} \left[f(x)g(x)\right] = \left[\lim_{x \rightarrow 0} f(x)\right] \left[\lim_{x \rightarrow 0} g(x) \right] = 0 \cdot \lim_{x \rightarrow 2} g(x) = 0$
4). $\lim_{x \rightarrow -1} \frac{f(x)}{g(x)}$ : $\lim_{x \rightarrow -1} g(x) = 0$이기 때문에 극한값이 정의되지 않는다.
5). $\lim_{x \rightarrow 2} \left[x^{3}f(x)\right] = \left[\lim_{x \rightarrow 2} x^{3}\right] \left[\lim_{x \rightarrow 2} f(x)\right]= 8 \cdot 2 = 16$
6). $\lim_{x \rightarrow 1} \sqrt{3 + f(x)} = \sqrt{3 + \lim_{x \rightarrow 1} f(x)} = \sqrt{4}= 2$
연습문제3. 극한값이 존재한다면 아래의 식들에 대한 극한값을 구하여라.
1). $\lim_{x \rightarrow -2} (3x^{4} + 2x^{2} - x + 1)$
2). $\lim_{x \rightarrow 2} \frac{2x^{2}+ 1}{x^{2} + 6x + 4}$
3). $\lim_{x \rightarrow 8} (1 + \sqrt[3]{x})(2 - 6x^{2} + x^{3})$
4). $\lim_{t \rightarrow -1} (t^{2} + 1)^{3}(t + 3)^{5}$
5). $\lim_{x \rightarrow 1} \left(\frac{1+ 3x}{1 + 4x^{2} + 3x^{4}}\right)^{3}$
6). $\lim_{u \rightarrow -2} \sqrt{u^{4} + 3u + 6}$
7). $\lim_{x \rightarrow 4^{-}} \sqrt{16 - x^{2}}$
1). $\lim_{x \rightarrow -2} (3x^{4} + 2x^{2} - x + 1) = 3 \cdot (-2)^{4} + 2 \cdot (-2)^{2} - (-2) + 1 = 59$
2). $\lim_{x \rightarrow 2} \frac{2x^{2}+ 1}{x^{2} + 6x + 4} = \frac{2 \cdot 2^{2} + 1}{2^{2} + 6 \cdot 2 + 1} = \frac{3}{4}$
3). $\lim_{x \rightarrow 8} (1 + \sqrt[3]{x})(2 - 6x^{2} + x^{3}) = (1 + \sqrt[3]{8})(1 - 6 \cdot 8^{2} + 8^{3}) =390$
4). $\lim_{t \rightarrow -1} (t^{2} + 1)^{3}(t + 3)^{5} = ((-1)^{2} + 1)^{3})((-1) + 3)^{5} = 2^{3}2^{5} = 2^{8} = 256$
5). $\lim_{x \rightarrow 1} \left(\frac{1+ 3x}{1 + 4x^{2} + 3x^{4}}\right)^{3} = \left(\frac{1 + 3}{1 + 4 + 3}\right)^{3}= \left(\frac{2}{3}\right)^{3} = \frac{8}{27}$
6). $\lim_{u \rightarrow -2} \sqrt{u^{4} + 3u + 6} = \sqrt{(-2)^{4} + 3 \cdot (-2) + 6} = \sqrt{16} = 4$
7). $\lim_{x \rightarrow 4^{-}} \sqrt{16 - x^{2}} = 0$
연습문제4. 극한값이 존재한다면 아래의 식들에 대한 극한값을 구하여라.
1). $\lim_{x \rightarrow 2} \frac{x^{2} + x - 6}{x - 2}$
2). $\lim_{x \rightarrow -4} \frac{x^{2} + 5x + 4}{x^{2} + 3x - 4}$
3). $\lim_{x \rightarrow 2} \frac{x^{2} - x + 6}{x - 2}$
4). $\lim_{x \rightarrow 4} \frac{x^{2} - 4x}{x^{2} - 3x - 4}$
5). $\lim_{t \rightarrow 3} \frac{t^{2} - 9}{2t^{2} + 7t + 3}$
6). $\lim_{x \rightarrow -1} \frac{x^{2} - 4x}{x^{2} - 3x - 4}$
7). $\lim_{h \rightarrow 0} \frac{(4 + h)^{2} - 16}{h}$
8). $\lim_{x \rightarrow 1} \frac{x^{3} - 1}{x^{2} - 1}$
9). $\lim_{x \rightarrow -2} \frac{x + 2}{x^{3} + 8}$
10). $\lim_{h \rightarrow 0} \frac{(2 + h)^{3} - 8}{h}$
1). $\lim_{x \rightarrow 2} \frac{x^{2} + x - 6}{x - 2} = \lim_{x \rightarrow 2} \frac{(x -2)(x + 3)}{x-2} = \lim_{x \rightarrow 2} (x + 3) = 5$
2). $\lim_{x \rightarrow -4} \frac{x^{2} + 5x + 4}{x^{2} + 3x - 4} = \lim_{x \rightarrow -4} \frac{(x + 1)(x + 4)}{(x + 4)(x - 1)} = \lim_{x \rightarrow -4} \frac{x + 1}{x - 1} = \frac{3}{5}$
3). $\lim_{x \rightarrow 2} \frac{x^{2} - x + 6}{x - 2} = \lim_{x \rightarrow 2} \frac{(x - 2)(x - 3)}{x- 2} = \lim_{x \rightarrow 2} (x - 3) = -1$
4). $\lim_{x \rightarrow 4} \frac{x^{2} - 4x}{x^{2} - 3x - 4} = \lim_{x \rightarrow 4} \frac{x(x-4)}{(x + 1)(x - 4)} = \lim_{x \rightarrow 4} \frac{x}{x + 1} = \frac{4}{5}$
5). $\lim_{t \rightarrow 3} \frac{t^{2} - 9}{2t^{2} + 7t + 3} =\lim_{t \rightarrow 3} \frac{(t - 3)(t + 3)}{(t + 3)(2t + 1)} = \lim_{t \rightarrow 3} \frac{t - 3}{2t + 1} = 0$
6). $\lim_{x \rightarrow -1} \frac{x^{2} - 4x}{x^{2} - 3x - 4} = \lim_{x \rightarrow -1} \frac{x(x- 4)}{(x - 4)(x + 1)} = \lim_{x \rightarrow -1} \frac{x}{x + 1} \rightarrow $ 분모가 0이기 때문에 정의되지 않는다.
7). $\lim_{h \rightarrow 0} \frac{(4 + h)^{2} - 16}{h} = \lim_{h \rightarrow 0} \frac{h(h + 8)}{h} = \lim_{h \rightarrow 0} (h + 8) = 8$
8). $\lim_{x \rightarrow 1} \frac{x^{3} - 1}{x^{2} - 1} = \lim_{x \rightarrow 1} \frac{(x-1)(x^{2} + x + 1)}{(x - 1)(x + 1)} = \lim_{x \rightarrow 1} \frac{x^{2} + x + 1}{x + 1} = \frac{3}{2}$
9). $\lim_{x \rightarrow -2} \frac{x + 2}{x^{3} + 8} = \lim_{x \rightarrow -2} \frac{x + 2}{(x + 2)(x^{2} + 2x + 4)} = \lim_{x \rightarrow -2} \frac{1}{x^{2} + 2x + 4} = \frac{1}{4}$
10). $\lim_{h \rightarrow 0} \frac{(2 + h)^{3} - 8}{h} = \lim_{h \rightarrow 0} \frac{(2+ h - 2)((2 + h)^{2} + 2(2 +h) + 4)}{h} = \lim_{h \rightarrow 0} (2 + h)^{2} +2(2 + h) + 4 = 12$
연습문제5. 극한값이 존재한다면 아래의 식들에 대한 극한값을 구하여라.
1). $\lim_{t \rightarrow 9} \frac{9 - t}{3- \sqrt{t}}$
2). $\lim_{h \rightarrow 0} \frac{\sqrt{1 + h}- 1}{h}$
3). $\lim_{x \rightarrow 7} \frac{\sqrt{x +2} - 3}{x- 7}$
4). $\lim_{x \rightarrow -1} \frac{x^{2} +2x + 1}{x^{4} - 1}$
5). $\lim_{x \rightarrow -4} \frac{\frac{1}{4} + \frac{1}{x}}{4 + x}$
6). $\lim_{t \rightarrow 0} \left(\frac{1}{t} - \frac{1}{t^{2} + t}\right)$
7). $\lim_{x \rightarrow 16} \frac{4 - \sqrt{x}}{16x - x^{2}}$
8). $\lim_{h \rightarrow 0} \frac{(3 + h)^{-1} - 3^{-1}}{h}$
9). $\lim_{t \rightarrow 0} \left(\frac{1}{t\sqrt{1 + t}} - \frac{1}{t}\right)$
10). $\lim_{x \rightarrow -4} \frac{\sqrt{x^{2} + 9} - 5}{x + 4}$
1). $\lim_{t \rightarrow 9} \frac{9 - t}{3- \sqrt{t}} = \lim_{t \rightarrow 9} \frac{(3 - \sqrt{t})(3 + \sqrt{t})}{3 - \sqrt{t}} = \lim_{t \rightarrow 9} (3 + \sqrt{t}) = 6$
2). $\lim_{h \rightarrow 0} \frac{\sqrt{1 + h}- 1}{h} = \lim_{h \rightarrow 0} \frac{(\sqrt{1 + h} - 1)(\sqrt{1 + h} + 1)}{h(\sqrt{1 + h} + 1)} = \lim_{h \rightarrow 0} \frac{1}{\sqrt{1 + h} + 1} = \frac{1}{2}$
3). $\lim_{x \rightarrow 7} \frac{\sqrt{x +2} - 3}{x- 7} = \lim_{x \rightarrow 7} \frac{(\sqrt{x + 2} - 3)(\sqrt{x + 2} + 3)}{(x - 7)(\sqrt{x + 2} + 3)} = \lim_{x \rightarrow 7} \frac{1}{\sqrt{x + 2} + 3} = \frac{1}{6}$
4). $\lim_{x \rightarrow -1} \frac{x^{2} +2x + 1}{x^{4} - 1} = \lim_{x \rightarrow -1} \frac{(x + 1)^{2}}{(x^{2} + 1)(x + 1)(x - 1)} = \lim_{x \rightarrow -1} \frac{x + 1}{(x^{2 + 1})(x - 1)} = 0$
5). $\lim_{x \rightarrow -4} \frac{\frac{1}{4} + \frac{1}{x}}{4 + x} = \lim_{x \rightarrow -4} \frac{\frac{4 + x}{4x}}{4 +x} = \lim_{x \rightarrow -4} \frac{1}{4x} = -\frac{1}{16}$
6). $\lim_{t \rightarrow 0} \left(\frac{1}{t} - \frac{1}{t^{2} + t}\right) = \lim_{t \rightarrow 0} \frac{1}{t}\left(1 - \frac{1}{1 +t}\right) = \lim_{t \rightarrow 0} \frac{1}{t} \cdot \frac{t}{1 + t} = \lim_{t \rightarrow 0} \frac{1}{1 + t} = 1$
7). $\lim_{x \rightarrow 16} \frac{4 - \sqrt{x}}{16x - x^{2}} = \lim_{x \rightarrow 16} \frac{4 - \sqrt{x}}{x(4 - \sqrt{x})(4 + \sqrt{x})} = \lim_{x \rightarrow 16} \frac{1}{x(4 + \sqrt{x})} = \frac{1}{128}$
8). $\lim_{h \rightarrow 0} \frac{(3 + h)^{-1} - 3^{-1}}{h} = \lim_{h \rightarrow 0} \frac{\frac{1}{3 + h} - \frac{1}{3}}{h} = \lim_{h \rightarrow 0} \frac{3 - (3 + h)}{3h(3 + h)} = \lim_{h \rightarrow 0} -\frac{1}{3(3 + h)} = -\frac{1}{9}$
9). $\lim_{t \rightarrow 0} \left(\frac{1}{t\sqrt{1 + t}} - \frac{1}{t}\right) = \lim_{t \rightarrow 0} \frac{1- \sqrt{1 + t}}{t\sqrt{1 + t}} = \lim_{t \rightarrow 0} \frac{(1- \sqrt{1 + t})(1 + \sqrt{1 + t})}{t\sqrt{1 + t}(1 + \sqrt{t})} = \lim_{t \rightarrow 0} -\frac{1}{\sqrt{1 + t}(1+ \sqrt{t})} = -\frac{1}{2}$
10). $\lim_{x \rightarrow -4} \frac{\sqrt{x^{2} + 9} - 5}{x + 4} = \lim_{x \rightarrow -4} \frac{(\sqrt{x^{2} + 9}-5)(\sqrt{x^{2} +9} + 5)}{(x + 4)(\sqrt{x^{2} + 9} + 5)} = \lim_{x \rightarrow -4} \frac{(x + 4)(x - 4)}{(x + 4)(\sqrt{x^{2} + 9} + 5)} = \lim_{x \rightarrow -4} \frac{x - 4}{\sqrt{x{2} + 9} + 5} = -\frac{4}{5}$
연습문제6. 극한값이 존재한다면 주어진 함수의 극한값을 구하여라.
1). $2x \le f(x) \le x^{4} - x^{2} + 2$일 때, $\lim_{x \rightarrow 1} f(x)$
2). $\lim_{x \rightarrow 0} x^{4}\cos\left(\frac{2}{x}\right)$
3). $\lim_{x \rightarrow 0^{+}} \sqrt{x}e^{\sin(\pi/x)}$
1). 임의의 $x \in \mathbb{R}$에 대해서 $2x \le f(x) \le x^{4} - x^{2} + 2$를 만족하기 때문에 극한값의 대소관계도 마찬가지로 부등식이 성립한다.
$$\begin{align*} &\lim_{x \rightarrow 1} 2x \le \lim_{x \rightarrow 1} f(x) \le \lim_{x \rightarrow 1} \left(x^{4} - x^{2} + 2\right) \Rightarrow &2 \le \lim_{x \rightarrow 1} f(x) \le 2\end{align*}$$
샌드위치 정리에 의해 $\lim_{x \rightarrow 1} f(x) = 1$이다.
2). 임의의 $x \in \mathbb{R}$에 대해서 $-1 \le \cos(x) \le 1$을 만족하기 때문에 $-x^{4} \le x^{4}\cos\left(\frac{2}{x}\right) \le x^{4}$가 성립한다. 이때, $\lim_{x \rightarrow 0} \left(-x^{4}\right) = \lim_{x \rightarrow 0} x^{4} = 0$이기 때문에 샌드위치 정리에 의해 $\lim_{x \rightarrow 0} x^{4}\cos\left(\frac{2}{x}\right) = 0$이다.
3). 임의의 $x \in \mathbb{R}$에 대해서 $-1 \le \sin(x) \le 1$을 만족하기 때문에 $\frac{\sqrt{x}}{e} \le \sqrt{x}e^{\sin(\pi/x)} \le \sqrt{x}e$가 성립한다. 이때, $\lim_{x \rightarrow 0^{+}} \frac{\sqrt{x}}{e} = \lim_{x \rightarrow 0^{+}} \sqrt{x}e = 0$이기 때문에 샌드위치 정리에 의해 $\lim_{x \rightarrow 0^{+}} \sqrt{x}e^{\sin(\pi/x)} = 0$이다.
연습문제7. 극한값이 존재한다면 아래의 식들에 대한 극한값을 구하여라.
1). $\lim_{x \rightarrow 3} \left(2x + |x - 3|\right)$
2). $\lim_{x \rightarrow -6} \frac{2x + 12}{|x + 6|}$
3). $\lim_{x \rightarrow 0.5} \frac{2x - 1}{|2x^{3} - x^{2}|}$
4). $\lim_{x \rightarrow -2} \frac{2 - |x|}{2 + x}$
5). $\lim_{x \rightarrow 0} \left(\frac{1}{x} - \frac{1}{|x|}\right)$
1). $\lim_{x \rightarrow 3} \left(2x + |x - 3|\right)$
좌극한 : $\lim_{x \rightarrow 3^{-}} \left(2x + |x - 3|\right) = \lim_{x \rightarrow 3^{-}} \left(2x + (-x + 3)\right) = \lim_{x \rightarrow 3^{-}} \left(x + 3\right) = 6$
우극한 : $\lim_{x \rightarrow 3^{+}} \left(2x + |x - 3|\right) = \lim_{x \rightarrow 3^{+}} \left(2x + (x - 3)\right) = \lim_{x \rightarrow 3^{+}} \left(3x - 3\right) = 6$
좌극한과 우극한의 값이 동일하기 때문에 $\lim_{x \rightarrow 3} \left(2x + |x - 3|\right) = 3$이다.
2). $\lim_{x \rightarrow -6} \frac{2x + 12}{|x + 6|}$
좌극한 : $\lim_{x \rightarrow -6^{-}} \frac{2x + 12}{|x + 6|} = \lim_{x \rightarrow -6^{-}} \frac{2(x + 6)}{-(x + 6)} = -2$
우극한 : $\lim_{x \rightarrow -6^{+}} \frac{2x + 12}{|x + 6|} = \lim_{x \rightarrow -6^{+}} \frac{2(x + 6)}{x + 6} = 2$
좌극한과 우극한의 값이 다르기 때문에 $\lim_{x \rightarrow -6} \frac{2x + 12}{|x + 6|}$은 존재하지 않는다.
3). $\lim_{x \rightarrow 0.5} \frac{2x - 1}{|2x^{3} - x^{2}|}$
좌극한 : $\lim_{x \rightarrow 0.5^{-}} \frac{2x - 1}{|2x^{3} - x^{2}|} = \lim_{x \rightarrow 0.5^{-}} \frac{2x - 1}{x^{2}(-2x + 1)} = \lim_{x \rightarrow 0.5^{-}} -\frac{1}{x^{2}} = -4$
우극한 : $\lim_{x \rightarrow 0.5^{+}} \frac{2x - 1}{|2x^{3} - x^{2}|} = \lim_{x \rightarrow 0.5^{+}} \frac{2x - 1}{x^{2}(2x - 1)} = \lim_{x \rightarrow 0.5^{+}} \frac{1}{x^{2}} = 4$
좌극한과 우극한의 값이 다르기 때문에 $\lim_{x \rightarrow 0.5} \frac{2x - 1}{|2x^{3} - x^{2}|}$은 존재하지 않는다.
4). $\lim_{x \rightarrow -2} \frac{2 - |x|}{2 + x}$
좌극한 : $\lim_{x \rightarrow -2^{-}} \frac{2 - |x|}{2 + x} = \lim_{x \rightarrow -2^{-}} \frac{2 + x}{2 + x} = 1$
우극한 : $\lim_{x \rightarrow -2^{+}} \frac{2 - |x|}{2 + x} = \lim_{x \rightarrow -2^{+}} \frac{2 + x}{2 + x} = 1$
좌극한과 우극한의 값이 동일하기 때문에 $\lim_{x \rightarrow -2} \frac{2 - |x|}{2 + x} = 1$이다.
5). $\lim_{x \rightarrow 0} \left(\frac{1}{x} - \frac{1}{|x|}\right)$
좌극한 : $\lim_{x \rightarrow 0^{-}} \left(\frac{1}{x} - \frac{1}{|x|}\right) = \lim_{x \rightarrow 0^{-}} \left(\frac{1}{x} + \frac{1}{x}\right) = \lim_{x \rightarrow 0^{-}} \frac{2}{x} = \infty$
우극한 : $\lim_{x \rightarrow 0^{+}} \left(\frac{1}{x} - \frac{1}{|x|}\right) = \lim_{x \rightarrow 0^{+}} \left(\frac{1}{x} - \frac{1}{x}\right) = \lim_{x \rightarrow 0^{+}} 0 = 0$
좌극한과 우극한의 값이 다르기 때문에 $\lim_{x \rightarrow 0} \left(\frac{1}{x} - \frac{1}{|x|}\right)$는 존재하지 않는다.
연습문제8. 임의의 실수 $x$에 대해서 $[x]$를 $x$보다 작은 최대 정수라고 정의할 때 아래의 식들에 대한 극한값을 구하여라.
1). $\lim_{x \rightarrow -2^{+}} [x]$
2). $\lim_{x \rightarrow -2} [x]$
3). $\lim_{x \rightarrow -2.4} [x]$
4). $\lim_{x \rightarrow n^{-}} [x]$
5). $\lim_{x \rightarrow n^{+}} [x]$
1). $\lim_{x \rightarrow -2^{+}} [x] = -2$
2). $\lim_{x \rightarrow -2} [x]$
좌극한 : $\lim_{x \rightarrow -2^{-}} [x] = -3$
우극한 : $\lim_{x \rightarrow -2^{+}} [x] = -2$
좌극한과 우극한의 값이 다르기 때문에 $\lim_{x \rightarrow -2} [x]$는 존재하지 않는다.
3). $\lim_{x \rightarrow -2.4} [x] = -3$
4). $\lim_{x \rightarrow n^{-}} [x] = n - 1$
4). $\lim_{x \rightarrow n^{+}} [x] = n$
연습문제9. $\lim_{x \rightarrow 1} \frac{f(x) - 8}{x - 1} = 10$일 때, $\lim_{x \rightarrow 1} f(x)$를 구하여라.
$g(x) = \frac{f(x) - 8}{x - 1}$이라고 하자. 이를 정리하면 $f(x) = (x - 1)g(x) + 8$이기 때문에 함수 $f$를 $x \rightarrow 1$로의 극한을 취해준다.
$$\lim_{x \rightarrow 1} f(x) = \lim_{x \rightarrow } \left[(x - 1)g(x) + 8\right] = 8$$
연습문제10. 아래와 같은 그림에서 $C_{1} : (x - 1)^{2} + y^{2} = 1$이고 $C_{2}$는 중심이 원점 $O$이고 반지름이 $r$인 원이라고 하자. 점 $P$를 원 $C_{2}$와 $y$축이 만나는 점, 점 $Q$를 두 원이 만날 때 위의 점, 점 $R$을 두 점 $P$와 $Q$를 지나는 직선과 $x$축이 만나는 점이라고 할 때 $r \rightarrow 0^{+}$를 취할 때 점 $R$의 위치를 구하여라.
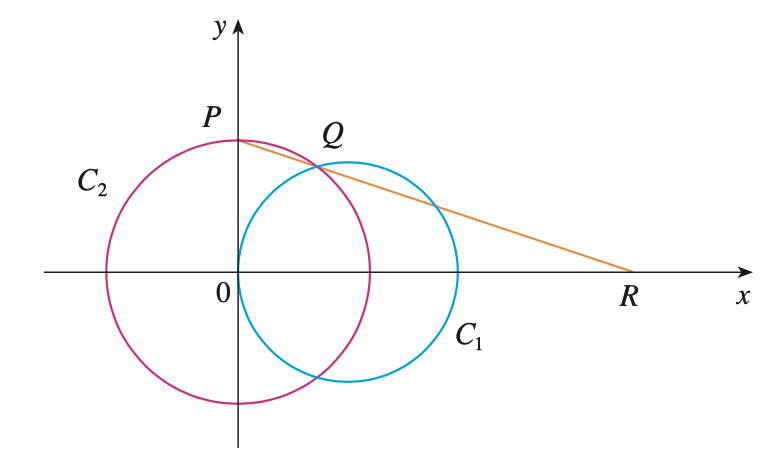
먼저 점 $P$는 원 $C_{2}$와 $y$축이 만나는 점이므로 $P(0, r)$이다. 이제, 점 $Q$를 구하기 위해 $C_{2} : x^{2} + y^{2} = r^{2}$이라고 하자. 이때, 두 원이 만나는 점은 $(x - 1)^{2} + y^{2} = 1$에 $x^{2} + y^{2} = r^{2}$을 대입하여 얻을 수 있다.
$$\begin{align*} &(x - 1)^{2} + (r^{2} - x^{2}) = 1 \\ \Rightarrow &(x - 1)^{2} - x^{2} = 1 - r^{2} \\ \Rightarrow &(x - 1 - x)(x - 1 + x) = 1 - r^{2} \\ \Rightarrow &2x - 1 = r^{2} - 1 \\ \Rightarrow& x = \frac{r^{2}}{2} \end{align*}$$
이제 얻은 $x$좌표를 원 $C_{2}$에 대입하여 $y$좌표를 구한다.
$$\begin{align*} &\left(\frac{r^{2}}{2}\right)^{2} + y^{2} = r^{2} \\ \Rightarrow&y^{2} = r^{2} - \frac{r^{4}}{4} \\ \Rightarrow& y = \pm \frac{r}{2}\sqrt{4 - r^{2}}\end{align*}$$
이때, 점 $Q$는 $y$좌표가 양수인 점이기 때문에 $y = \frac{r}{2}\sqrt{4 - r^{2}}$이다. 마지막으로 점 $P$와 $Q$를 지나는 직선 $PQ$의 $x$절편을 구하면 된다. 이를 위해 직선 $PQ$를 기울기 $m$과 편향 $b$을 갖는 직선 $y = mx + b$라고 정의하자. 여기서, 직선 $PQ$는 점 $P$를 지나기 때문에 $y$절편은 $b = r$이다. 이제 점 $Q$를 대입하여 기울기 $m$을 찾는다.
$$\begin{align*} &\frac{r}{2}\sqrt{4 - r^{2}} = m \frac{r^{2}}{2} + r \\ \Rightarrow& \frac{r^{2}}{2}m = \frac{r}{2}\sqrt{4 - r^{2}} - r \\ \Rightarrow&m = \frac{2}{r^{2}} \left(\frac{r}{2}\sqrt{4 - r^{2}} - r \right)\end{align*}$$
마지막으로 직선 $PQ$의 $x$절편은 $y = 0$이라고 할 때 얻을 수 있으므로 $x(r) = \frac{r}{m} = \frac{r}{\frac{2}{r^{2}} \left(\frac{r}{2}\sqrt{4 - r^{2}} - r\right)} = \frac{r^{2}}{\sqrt{4 - r^{2}} - 2}$이다. 이제 $x(r)$에 $r \rightarrow 0^{+}$로의 극한을 취해준다.
$$\begin{align*} \lim_{r \rightarrow 0^{+}} \frac{r^{2}}{\sqrt{4 - r^{2}} - 2} &= \lim_{r \rightarrow 0^{+}} \frac{r^{2}}{\sqrt{4 - r^{2}} - 2} \cdot \frac{\sqrt{4 - r^{2}} + 2}{\sqrt{4 - r^{2}} + 2} \\ &= \lim_{r \rightarrow 0^{+}} \frac{r^{2}\left(\sqrt{4 - r^{2}} + 2\right)}{r^{2}} \\ &= \lim_{r \rightarrow 0^{+}} \left(\sqrt{4 - r^{2}} + 2\right) = 4\end{align*}$$
따라서, $r \rightarrow 0^{+}$일 때 $R(x(r), 0) \rightarrow R(4, 0)$이다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.07.06 : 연습문제1-5 추가
22.07.08 : 연습문제6-10 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 연속함수 (1) | 2021.08.29 |
|---|---|
| 미적분학 - 정확한 극한의 정의 (0) | 2021.08.25 |
| 미적분학 - 함수의 극한 (0) | 2021.08.17 |
| 미적분학 - 접선 (0) | 2021.08.16 |
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
안녕하세요. 지난 포스팅의 미적분학 - 함수의 극한에서는 극한을 간단하게 정의하고 계산해보았습니다. 오늘은 극한 법칙과 이를 활용한 극한 계산법에 대해서 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
일단 limx→af(x)와 limx→ag(x)가 존재한다고 가정하겠습니다. 그러면 아래의 법칙들이 성립합니다.
- limx→a[f(x)±g(x)]=limx→af(x)±limx→ag(x)
- limx→a[cf(x)]=climx→f(x)
- limx→a[f(x)g(x)]=[limx→af(x)][limx→ag(x)]
- limx→af(x)g(x)=limx→af(x)limx→ag(x)(이때, limx→g(x)≠0 이여야 합니다!)
- limx→a[f(x)]n=[limx→af(x)]n
- limx→ac=c
- limx→an√f(x)=n√limx→af(x)
예제1.limx→2f(x)=4,limx→2g(x)=−2,limx→2h(x)=0이라고 할 때 아래의 식을 계산하시오.
- limx→2[f(x)+5g(x)]
- limx→23f(x)g(x)
- limx→2g(x)h(x)
1. limx→2[f(x)+5g(x)]=limx→2f(x)+limx→25g(x)=limx→2f(x)+5limx→2g(x)=4+5⋅(−2)=−6
2. limx→23f(x)g(x)=limx→23f(x)limx→2g(x)=3limx→2f(x)limx→2g(x)=3⋅4−2=−6
3. limx→2h(x)=0이기 때문에 극한은 정의되지 않는다.
예제2.limx→2√6−x−2√3−x−1을 계산하라.
limx→2√6−x−2√3−x−1=limx→2(√6−x−2)(√3−x+1)(√3−x−1)(√3−x+1)=limx→2(√6−x−2)(√3−x+1)2−x=limx→2(√6−x−2)2−x⋅(√3−x+1)=limx→2√6−x−22−xlimx→2(√3−x+1)=2limx→2√6−x−22−x=2limx→2(√6−x−2)(√6−x+2)(2−x)(√6−x+2)=2limx→22−x(2−x)(√6−x+2)=2limx→21√6−x+2=24=12
또한 만약 두 함수 사이의 대소 관계가 명확하면 아래의 법칙들도 성립합니다. f(x)≤h(x)≤g(x)라고 가정하겠습니다.
- limx→af(x)≤limx→ag(x)
- limx→af(x)=limx→ag(x)=L⇒limx→ah(x)=L
연습문제1. 각 함수 f,g,h에 대해서 limx→2f(x)=4,limx→2g(x)=−2,limx→2h(x)=0이 성립한다고 가정했을 때 아래의 식들을 구하여라.
1). limx→2[f(x)+5g(x)]
2). limx→2[g(x)]3
3). limx→2√f(x)
4). limx→23f(x)g(x)
5). limx→2g(x)h(x)
6). limx→2g(x)h(x)f(x)
1). limx→2[f(x)+5g(x)]=limx→2f(x)+5limx→2g(x)=4+5⋅(−2)=−6
2). limx→2[g(x)]3=[limx→2g(x)]3=(−2)3=−8
3). limx→2√f(x)=√limx→2f(x)=√4=2
4). limx→23f(x)g(x)=3limx→2f(x)limx→2g(x)=−6
5). limx→2g(x)h(x) : limx→2h(x)=0이기 때문에 정의되지 않는다.
6). limx→2g(x)h(x)f(x)=[limx→2g(x)][limx→2h(x)]limx→2f(x)=(−2)⋅04=0
연습문제2. 각 함수 f와 g가 아래의 그래프로 주어져있을 때 아래의 식들을 구하여라.
1). limx→2[f(x)+g(x)]
2). limx→1[f(x)+g(x)]
3). limx→0[f(x)g(x)]
4). limx→−1f(x)g(x)
5). limx→2[x3f(x)]
6). limx→1√3+f(x)

1). limx→2[f(x)+g(x)]=limx→2f(x)+limx→2g(x)=2+0=2
2). limx→1[f(x)+g(x)]:\lim_{x \rightarrow 1} g(x)$의 좌극한과 우극한이 달라 극한값이 정의되지 않는다.
3). limx→0[f(x)g(x)]=[limx→0f(x)][limx→0g(x)]=0⋅limx→2g(x)=0
4). limx→−1f(x)g(x) : limx→−1g(x)=0이기 때문에 극한값이 정의되지 않는다.
5). limx→2[x3f(x)]=[limx→2x3][limx→2f(x)]=8⋅2=16
6). limx→1√3+f(x)=√3+limx→1f(x)=√4=2
연습문제3. 극한값이 존재한다면 아래의 식들에 대한 극한값을 구하여라.
1). limx→−2(3x4+2x2−x+1)
2). limx→22x2+1x2+6x+4
3). limx→8(1+3√x)(2−6x2+x3)
4). limt→−1(t2+1)3(t+3)5
5). limx→1(1+3x1+4x2+3x4)3
6). limu→−2√u4+3u+6
7). limx→4−√16−x2
1). limx→−2(3x4+2x2−x+1)=3⋅(−2)4+2⋅(−2)2−(−2)+1=59
2). limx→22x2+1x2+6x+4=2⋅22+122+6⋅2+1=34
3). limx→8(1+3√x)(2−6x2+x3)=(1+3√8)(1−6⋅82+83)=390
4). limt→−1(t2+1)3(t+3)5=((−1)2+1)3)((−1)+3)5=2325=28=256
5). limx→1(1+3x1+4x2+3x4)3=(1+31+4+3)3=(23)3=827
6). limu→−2√u4+3u+6=√(−2)4+3⋅(−2)+6=√16=4
7). limx→4−√16−x2=0
연습문제4. 극한값이 존재한다면 아래의 식들에 대한 극한값을 구하여라.
1). limx→2x2+x−6x−2
2). limx→−4x2+5x+4x2+3x−4
3). limx→2x2−x+6x−2
4). limx→4x2−4xx2−3x−4
5). limt→3t2−92t2+7t+3
6). limx→−1x2−4xx2−3x−4
7). limh→0(4+h)2−16h
8). limx→1x3−1x2−1
9). limx→−2x+2x3+8
10). limh→0(2+h)3−8h
1). limx→2x2+x−6x−2=limx→2(x−2)(x+3)x−2=limx→2(x+3)=5
2). limx→−4x2+5x+4x2+3x−4=limx→−4(x+1)(x+4)(x+4)(x−1)=limx→−4x+1x−1=35
3). limx→2x2−x+6x−2=limx→2(x−2)(x−3)x−2=limx→2(x−3)=−1
4). limx→4x2−4xx2−3x−4=limx→4x(x−4)(x+1)(x−4)=limx→4xx+1=45
5). limt→3t2−92t2+7t+3=limt→3(t−3)(t+3)(t+3)(2t+1)=limt→3t−32t+1=0
6). limx→−1x2−4xx2−3x−4=limx→−1x(x−4)(x−4)(x+1)=limx→−1xx+1→ 분모가 0이기 때문에 정의되지 않는다.
7). limh→0(4+h)2−16h=limh→0h(h+8)h=limh→0(h+8)=8
8). limx→1x3−1x2−1=limx→1(x−1)(x2+x+1)(x−1)(x+1)=limx→1x2+x+1x+1=32
9). limx→−2x+2x3+8=limx→−2x+2(x+2)(x2+2x+4)=limx→−21x2+2x+4=14
10). limh→0(2+h)3−8h=limh→0(2+h−2)((2+h)2+2(2+h)+4)h=limh→0(2+h)2+2(2+h)+4=12
연습문제5. 극한값이 존재한다면 아래의 식들에 대한 극한값을 구하여라.
1). limt→99−t3−√t
2). limh→0√1+h−1h
3). limx→7√x+2−3x−7
4). limx→−1x2+2x+1x4−1
5). limx→−414+1x4+x
6). limt→0(1t−1t2+t)
7). limx→164−√x16x−x2
8). limh→0(3+h)−1−3−1h
9). limt→0(1t√1+t−1t)
10). limx→−4√x2+9−5x+4
1). limt→99−t3−√t=limt→9(3−√t)(3+√t)3−√t=limt→9(3+√t)=6
2). limh→0√1+h−1h=limh→0(√1+h−1)(√1+h+1)h(√1+h+1)=limh→01√1+h+1=12
3). limx→7√x+2−3x−7=limx→7(√x+2−3)(√x+2+3)(x−7)(√x+2+3)=limx→71√x+2+3=16
4). limx→−1x2+2x+1x4−1=limx→−1(x+1)2(x2+1)(x+1)(x−1)=limx→−1x+1(x2+1)(x−1)=0
5). limx→−414+1x4+x=limx→−44+x4x4+x=limx→−414x=−116
6). limt→0(1t−1t2+t)=limt→01t(1−11+t)=limt→01t⋅t1+t=limt→011+t=1
7). limx→164−√x16x−x2=limx→164−√xx(4−√x)(4+√x)=limx→161x(4+√x)=1128
8). limh→0(3+h)−1−3−1h=limh→013+h−13h=limh→03−(3+h)3h(3+h)=limh→0−13(3+h)=−19
9). limt→0(1t√1+t−1t)=limt→01−√1+tt√1+t=limt→0(1−√1+t)(1+√1+t)t√1+t(1+√t)=limt→0−1√1+t(1+√t)=−12
10). limx→−4√x2+9−5x+4=limx→−4(√x2+9−5)(√x2+9+5)(x+4)(√x2+9+5)=limx→−4(x+4)(x−4)(x+4)(√x2+9+5)=limx→−4x−4√x2+9+5=−45
연습문제6. 극한값이 존재한다면 주어진 함수의 극한값을 구하여라.
1). 2x≤f(x)≤x4−x2+2일 때, limx→1f(x)
2). limx→0x4cos(2x)
3). limx→0+√xesin(π/x)
1). 임의의 x∈R에 대해서 2x≤f(x)≤x4−x2+2를 만족하기 때문에 극한값의 대소관계도 마찬가지로 부등식이 성립한다.
limx→12x≤limx→1f(x)≤limx→1(x4−x2+2)⇒2≤limx→1f(x)≤2
샌드위치 정리에 의해 limx→1f(x)=1이다.
2). 임의의 x∈R에 대해서 −1≤cos(x)≤1을 만족하기 때문에 −x4≤x4cos(2x)≤x4가 성립한다. 이때, limx→0(−x4)=limx→0x4=0이기 때문에 샌드위치 정리에 의해 limx→0x4cos(2x)=0이다.
3). 임의의 x∈R에 대해서 −1≤sin(x)≤1을 만족하기 때문에 √xe≤√xesin(π/x)≤√xe가 성립한다. 이때, limx→0+√xe=limx→0+√xe=0이기 때문에 샌드위치 정리에 의해 limx→0+√xesin(π/x)=0이다.
연습문제7. 극한값이 존재한다면 아래의 식들에 대한 극한값을 구하여라.
1). limx→3(2x+|x−3|)
2). limx→−62x+12|x+6|
3). limx→0.52x−1|2x3−x2|
4). limx→−22−|x|2+x
5). limx→0(1x−1|x|)
1). limx→3(2x+|x−3|)
좌극한 : limx→3−(2x+|x−3|)=limx→3−(2x+(−x+3))=limx→3−(x+3)=6
우극한 : limx→3+(2x+|x−3|)=limx→3+(2x+(x−3))=limx→3+(3x−3)=6
좌극한과 우극한의 값이 동일하기 때문에 limx→3(2x+|x−3|)=3이다.
2). limx→−62x+12|x+6|
좌극한 : limx→−6−2x+12|x+6|=limx→−6−2(x+6)−(x+6)=−2
우극한 : limx→−6+2x+12|x+6|=limx→−6+2(x+6)x+6=2
좌극한과 우극한의 값이 다르기 때문에 limx→−62x+12|x+6|은 존재하지 않는다.
3). limx→0.52x−1|2x3−x2|
좌극한 : limx→0.5−2x−1|2x3−x2|=limx→0.5−2x−1x2(−2x+1)=limx→0.5−−1x2=−4
우극한 : limx→0.5+2x−1|2x3−x2|=limx→0.5+2x−1x2(2x−1)=limx→0.5+1x2=4
좌극한과 우극한의 값이 다르기 때문에 limx→0.52x−1|2x3−x2|은 존재하지 않는다.
4). limx→−22−|x|2+x
좌극한 : \lim_{x \rightarrow -2^{-}} \frac{2 - |x|}{2 + x} = \lim_{x \rightarrow -2^{-}} \frac{2 + x}{2 + x} = 1
우극한 : \lim_{x \rightarrow -2^{+}} \frac{2 - |x|}{2 + x} = \lim_{x \rightarrow -2^{+}} \frac{2 + x}{2 + x} = 1
좌극한과 우극한의 값이 동일하기 때문에 \lim_{x \rightarrow -2} \frac{2 - |x|}{2 + x} = 1이다.
5). \lim_{x \rightarrow 0} \left(\frac{1}{x} - \frac{1}{|x|}\right)
좌극한 : \lim_{x \rightarrow 0^{-}} \left(\frac{1}{x} - \frac{1}{|x|}\right) = \lim_{x \rightarrow 0^{-}} \left(\frac{1}{x} + \frac{1}{x}\right) = \lim_{x \rightarrow 0^{-}} \frac{2}{x} = \infty
우극한 : \lim_{x \rightarrow 0^{+}} \left(\frac{1}{x} - \frac{1}{|x|}\right) = \lim_{x \rightarrow 0^{+}} \left(\frac{1}{x} - \frac{1}{x}\right) = \lim_{x \rightarrow 0^{+}} 0 = 0
좌극한과 우극한의 값이 다르기 때문에 \lim_{x \rightarrow 0} \left(\frac{1}{x} - \frac{1}{|x|}\right)는 존재하지 않는다.
연습문제8. 임의의 실수 x에 대해서 [x]를 x보다 작은 최대 정수라고 정의할 때 아래의 식들에 대한 극한값을 구하여라.
1). \lim_{x \rightarrow -2^{+}} [x]
2). \lim_{x \rightarrow -2} [x]
3). \lim_{x \rightarrow -2.4} [x]
4). \lim_{x \rightarrow n^{-}} [x]
5). \lim_{x \rightarrow n^{+}} [x]
1). \lim_{x \rightarrow -2^{+}} [x] = -2
2). \lim_{x \rightarrow -2} [x]
좌극한 : \lim_{x \rightarrow -2^{-}} [x] = -3
우극한 : \lim_{x \rightarrow -2^{+}} [x] = -2
좌극한과 우극한의 값이 다르기 때문에 \lim_{x \rightarrow -2} [x]는 존재하지 않는다.
3). \lim_{x \rightarrow -2.4} [x] = -3
4). \lim_{x \rightarrow n^{-}} [x] = n - 1
4). \lim_{x \rightarrow n^{+}} [x] = n
연습문제9. \lim_{x \rightarrow 1} \frac{f(x) - 8}{x - 1} = 10일 때, \lim_{x \rightarrow 1} f(x)를 구하여라.
g(x) = \frac{f(x) - 8}{x - 1}이라고 하자. 이를 정리하면 f(x) = (x - 1)g(x) + 8이기 때문에 함수 f를 x \rightarrow 1로의 극한을 취해준다.
\lim_{x \rightarrow 1} f(x) = \lim_{x \rightarrow } \left[(x - 1)g(x) + 8\right] = 8
연습문제10. 아래와 같은 그림에서 C_{1} : (x - 1)^{2} + y^{2} = 1이고 C_{2}는 중심이 원점 O이고 반지름이 r인 원이라고 하자. 점 P를 원 C_{2}와 y축이 만나는 점, 점 Q를 두 원이 만날 때 위의 점, 점 R을 두 점 P와 Q를 지나는 직선과 x축이 만나는 점이라고 할 때 r \rightarrow 0^{+}를 취할 때 점 R의 위치를 구하여라.
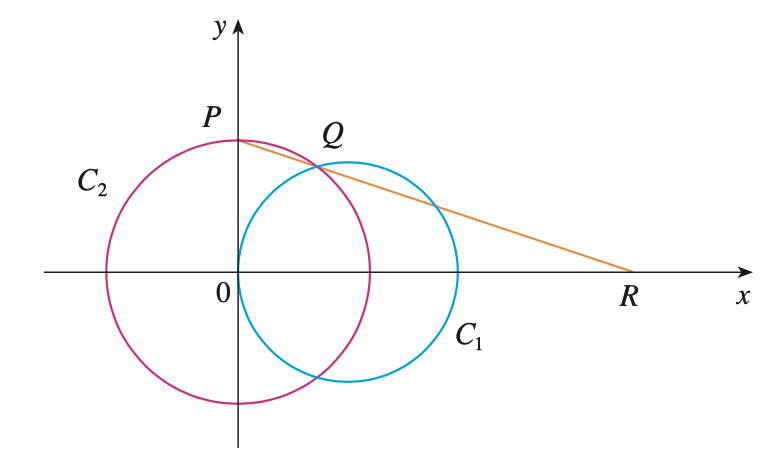
먼저 점 P는 원 C_{2}와 y축이 만나는 점이므로 P(0, r)이다. 이제, 점 Q를 구하기 위해 C_{2} : x^{2} + y^{2} = r^{2}이라고 하자. 이때, 두 원이 만나는 점은 (x - 1)^{2} + y^{2} = 1에 x^{2} + y^{2} = r^{2}을 대입하여 얻을 수 있다.
\begin{align*} &(x - 1)^{2} + (r^{2} - x^{2}) = 1 \\ \Rightarrow &(x - 1)^{2} - x^{2} = 1 - r^{2} \\ \Rightarrow &(x - 1 - x)(x - 1 + x) = 1 - r^{2} \\ \Rightarrow &2x - 1 = r^{2} - 1 \\ \Rightarrow& x = \frac{r^{2}}{2} \end{align*}
이제 얻은 x좌표를 원 C_{2}에 대입하여 y좌표를 구한다.
\begin{align*} &\left(\frac{r^{2}}{2}\right)^{2} + y^{2} = r^{2} \\ \Rightarrow&y^{2} = r^{2} - \frac{r^{4}}{4} \\ \Rightarrow& y = \pm \frac{r}{2}\sqrt{4 - r^{2}}\end{align*}
이때, 점 Q는 y좌표가 양수인 점이기 때문에 y = \frac{r}{2}\sqrt{4 - r^{2}}이다. 마지막으로 점 P와 Q를 지나는 직선 PQ의 x절편을 구하면 된다. 이를 위해 직선 PQ를 기울기 m과 편향 b을 갖는 직선 y = mx + b라고 정의하자. 여기서, 직선 PQ는 점 P를 지나기 때문에 y절편은 b = r이다. 이제 점 Q를 대입하여 기울기 m을 찾는다.
\begin{align*} &\frac{r}{2}\sqrt{4 - r^{2}} = m \frac{r^{2}}{2} + r \\ \Rightarrow& \frac{r^{2}}{2}m = \frac{r}{2}\sqrt{4 - r^{2}} - r \\ \Rightarrow&m = \frac{2}{r^{2}} \left(\frac{r}{2}\sqrt{4 - r^{2}} - r \right)\end{align*}
마지막으로 직선 PQ의 x절편은 y = 0이라고 할 때 얻을 수 있으므로 x(r) = \frac{r}{m} = \frac{r}{\frac{2}{r^{2}} \left(\frac{r}{2}\sqrt{4 - r^{2}} - r\right)} = \frac{r^{2}}{\sqrt{4 - r^{2}} - 2}이다. 이제 x(r)에 r \rightarrow 0^{+}로의 극한을 취해준다.
\begin{align*} \lim_{r \rightarrow 0^{+}} \frac{r^{2}}{\sqrt{4 - r^{2}} - 2} &= \lim_{r \rightarrow 0^{+}} \frac{r^{2}}{\sqrt{4 - r^{2}} - 2} \cdot \frac{\sqrt{4 - r^{2}} + 2}{\sqrt{4 - r^{2}} + 2} \\ &= \lim_{r \rightarrow 0^{+}} \frac{r^{2}\left(\sqrt{4 - r^{2}} + 2\right)}{r^{2}} \\ &= \lim_{r \rightarrow 0^{+}} \left(\sqrt{4 - r^{2}} + 2\right) = 4\end{align*}
따라서, r \rightarrow 0^{+}일 때 R(x(r), 0) \rightarrow R(4, 0)이다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.07.06 : 연습문제1-5 추가
22.07.08 : 연습문제6-10 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 연속함수 (1) | 2021.08.29 |
|---|---|
| 미적분학 - 정확한 극한의 정의 (0) | 2021.08.25 |
| 미적분학 - 함수의 극한 (0) | 2021.08.17 |
| 미적분학 - 접선 (0) | 2021.08.16 |
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
