안녕하세요. 지난 포스팅의 미적분학- 극한의 정확한 정의에서는 좌극한, 우극한의 정의와 함께 무한대로 발산하는 경우의 정의까지 알아보았습니다. 오늘은 극한을 통해 정의되는 새로운 함수의 종류인 연속함수 (continuous function)에 대해서 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
정의1. 연속함수 (Continuous functions)와 불연속 함수 (Discontinuous function)
함수 $f$가 $\lim_{x \rightarrow a} f(x) = f(a)$라면 $f$를 $x = a$에서의 연속함수 (continuous function)이라고 한다. 만약, $\lim_{x \rightarrow a} f(x) \neq f(a)$라면 $f$를 $x = a$에서의 불연속 함수 (discontinuous function)이라고 한다.
설명
연속함수는 아마 다들 어느정도 이해하실거라고 생각합니다. 아마도 대부분이 연속함수란 정의역에서 함수가 끊기지 않고 모두 연결되어있는 함수로 생각하실 겁니다. 이 정도도 사실은 충분하지만 어떻게 하면 좀 더 수학적으로 정의해 볼 수 있을까요? 이를 위해 저희는 "함수가 끊어지지 않는다."라는 특징에 집중할 필요가 있습니다.
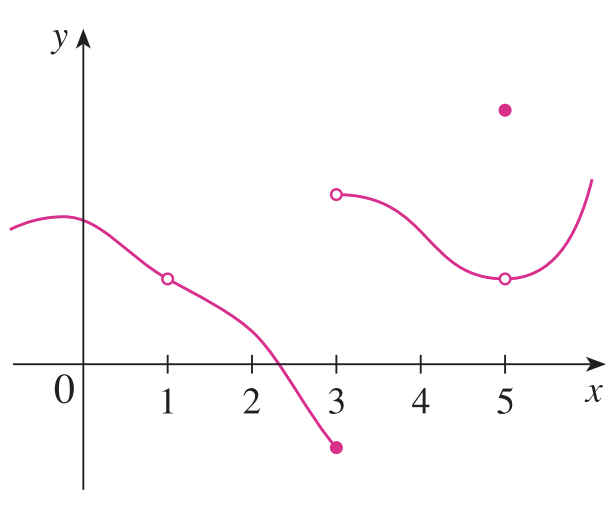
일단, 함수가 $x = a$에서 "끊겼다."라는 것은 함수가 연결되어 있지 않다는 의미이고 이는 위의 그림과 같이 세 가지 케이스로 나누어서 생각해볼 수 있습니다. 먼저, 가장 왼쪽의 $x = 1$처럼 $f(x)$가 $x = a$에서 정의가 되지 않는 경우입니다. 이 경우에는 $x = a$에서 $f(x)$가 그냥 구멍이 뚫려있습니다. 다음으로 생각해볼 수 있는 것은 $f(x)$가 $x = a$에서 정의는 되어있지만 끊겨있는 경우가 있을까요? 이를 위해 극한이 필요합니다. 다시 상기하면 극한이란 $x =\neq a$이지만 $x$가 $a$로 한없이 가까워질 때 얻을 수 있는 값이 됩니다. 그런데 만약 극한값이 존재하지 않는다면 가운데의 $x = 3$과 같이 될 것 입니다. 마지막으로는 $x = 5$와 같이 극한값은 존재하지만 함숫값과 다른 경우도 문제가 됩니다. 따라서 이러한 조건을 모두 피하는 것이 바로 "$\lim_{x \rightarrow a} f(x) = f(a)$"이고 이 조건을 만족하면 함수 $f(x)$를 연속함수라고 합니다.
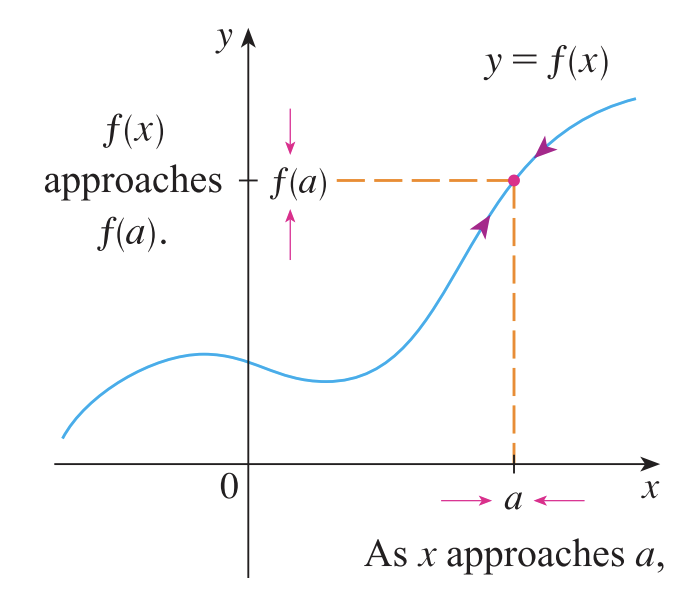
위 그림은 연속 함수를 그림으로 표현한 것 입니다. $x = a$를 중심으로 양쪽에서 접근했을 때 그에 대응되는 함숫값 역시 $f(a)$에 무한히 가까워지게 될 것 입니다. 지금까지 본 것은 "하나의 점"에서만 연속 조건을 만족하는 경우입니다. 그리고 이러한 점들을 모아서 구간을 만들면 함수 $f$는 구간에서 연속 함수라고 부를 수 있습니다. 예를 들어 $f(x)= x$ 함수는 모든 실수점에서 연속함수이기 때문에 $\mathbb{R}$에서 연속함수라고 말할 수 있습니다. 즉, 저희는 지난 포스팅의 미적분학 - 정확한 극한의 정의에서 보았던 엡실론-델타 논법을 다시 한번 적용해야하는 것을 알 수 있습니다.
정의1-1. 연속함수와 엡실론-델타 논법
함수 $f$가 임의의 양수 $\epsilon > 0$에 대해서 $|x - a| < \delta$일 때 $|f(x) - f(a)| < \epsilon$을 만족하는 $\delta > 0$가 존재하면 함수 $f$는 $x = a$에서 연속이라고 한다.
연속함수에는 저희가 이후에 함수를 좀 더 쉽게 다룰 수 있도록 도와주는 유용한 성질들이 있습니다. 차근차근 살펴보도록 하죠.
정리1. 연속함수의 판별
- 만약 함수 $f$와 $g$가 $x = a$에서 연속함수이고 $c$가 상수라면 $f \pm g, cf, fg, \frac{f}{g}$는 연속함수이다.
- 임의의 다항함수는 모든 실수 $\mathbb{R}$에서 연속함수이다.
- 다항함수, 유리함수, 제곱근함수, 삼각함수, 역삼각함수, 지수함수, 로그함수 모두 정의된 정의역에서 연속함수이다.
정리2.
만약 $f$가 $x = b$에서 연속이고 $\lim_{x \rightarrow a} g(x) = b$이면 $\lim_{x \rightarrow} f(g(x)) = f(b)$이다.
$$\lim_{x \rightarrow a} f(g(x)) = f(\lim_{x \rightarrow a} g(x))$$
설명
정리2의 증명은 간단합니다. 연속와 합성함수의 정의를 차근차근 적용해보면 됩니다. 먼적, 함수 $f$가 $x = b$에서 연속함수이기 때문에 임의의 양의 실수 $\epsilon > 0$에 대해서 $|x - b| < \delta_{1}$일 때 $|f(x) - f(b)| < \epsilon$을 만족하는 $\delta_{1} > 0$가 존재합니다. 또한, $\lim_{x \rightarrow a} g(x) = b$이기 때문에 극한의 정의에 의해 $|x - a| < \delta_{2}$일 때 $|g(x) - g(a)| < \delta_{1}$을 만족하는 $\delta_{2} > 0$가 존재하죠.
$\delta = \text{min}\{\delta_{1}, \delta_{2}\}$라고 하도록 하겠습니다. $|x - a| < \delta$일 때 $|g(x) - b| < \delta_{1}$을 만족하고 $g(x) = y$라고 할 때 $|f(y) - f(b)| < \epsilon$을 만족하기 때문에 $\lim_{x \rightarrow a} f(g(x)) = f(b)$입니다.
정리3. 합성함수의 연속성
함수 $g$가 $x = a$에서 연속이고 함수 $f$가 $x = g(a)$에서 연속이라고 하면 $(f \circ g)(x) = f(g(x))$로 정의되는 합성함수 $f \circ g$는 $x = a$에서 연속이다.
설명
정리3을 증명해보도록 하겠습니다. 함수 $g$가 점 $x = a$에서 연속이기 때문에 $\lim_{x \rightarrow a} g(x) = g(a)$입니다. 또한, 함수 $f$가 점 $x = b = g(a)$에서 연속이기 때문에 $\lim_{x \rightarrow a} f(g(x)) = f(g(a))$가 되죠. 이것은 $h = f \circ g$라고 했을 때 함수 $h$가 점 $x = a$에서 연속인 것과 동일한 의미이므로 $f \circ g$는 점 $x = a$에서 연속이 됩니다.
예제1.$\lim_{x \rightarrow 1} \arcsin{\left(\frac{1 - \sqrt{x}}{1 - x}\right)}$의 값을 구하여라.
$\lim_{x \rightarrow 1} \arcsin{\left(\frac{1- \sqrt{x}}{1 - x}\right)} = \arcsin{\lim_{x \rightarrow 1} \left(\frac{1 - \sqrt{x}}{1 - x}\right)}$를 만족한다.
$$\begin{align*} \lim_{x \rightarrow 1} \arcsin{\left(\frac{1 - \sqrt{x}}{1- x}\right)} &= \arcsin{\lim_{x \rightarrow 1} \left(\frac{1 - \sqrt{x}}{1 - x}\right)} \\ &= \arcsin{\lim_{x \rightarrow 1} \left(\frac{1 - \sqrt{x}}{(1 - \sqrt{x})(1 + \sqrt{x})}\right)} \\ &= \arcsin{\lim_{x \rightarrow 1} \left(\frac{1}{1 + \sqrt{x}}\right)} \\ &= \arcsin{\frac{1}{2}} = \frac{\pi}{6} \end{align*}$$
정리4. 중간값 정리 (Intermediate Value Theorem; IVT)
$f$가 닫힌 구간 $[a, b]$에서 연속이고 $N$을 $f(a)$와 $f(b)$ 사이의 임의의 숫자라고 가정하면(이때, $f(a) \neq f(b)$이다.) $f(c) = N$을 만족하는 $c$가 열린 구간 $(a, b)$에 존재한다.
설명
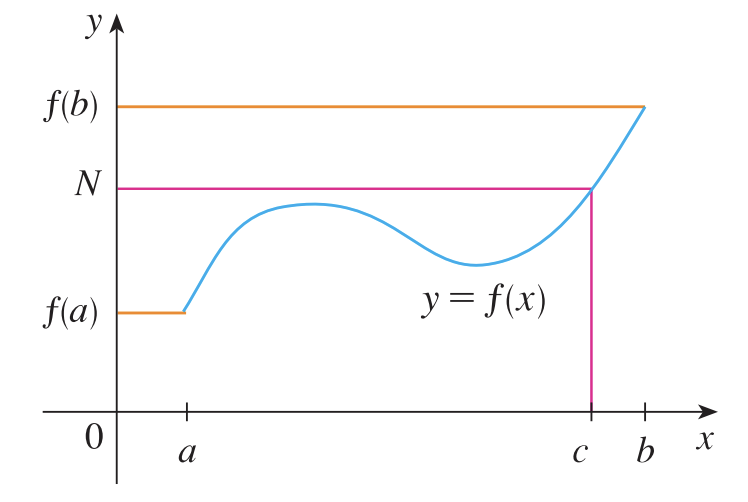
중간값 정리를 그림으로 그려보면 위와 같습니다. 아주 명확한 그림이죠. 중간값 정리는 이후에 다양한 증명에서 활용되기 때문에 꼭 알아두셔야하는 정리 중 하나입니다.
특히,IVT가 가장 많이 활용되는 증명 중 하나는 특정 구간에서 해의 존재성을 판단하는 것입니다. 예를 들어, $f(a) < 0$이고 $f(b) > 0$인 연속함수 $f$가 주어졌을 때 IVT에 의해서 함수 $f$는 열린 구간 $(a, b)$에서 $f(c) = 0$을 만족하는 $x = c$를 찾을 수 있다는 것을 알려줍니다. 이와 같은 방법으로 앞으로 다양한 문제들을 풀 수 있습니다.
연습문제1. 아래의 두 그래프에 대해서 물음에 답하여라.
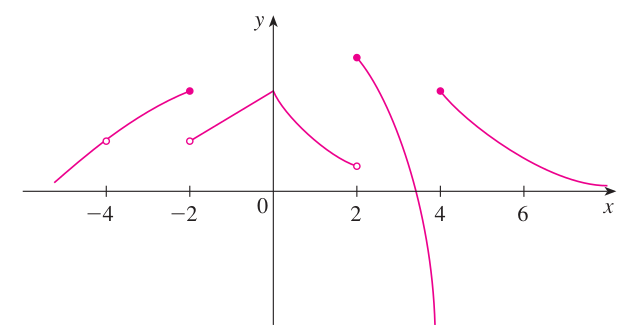
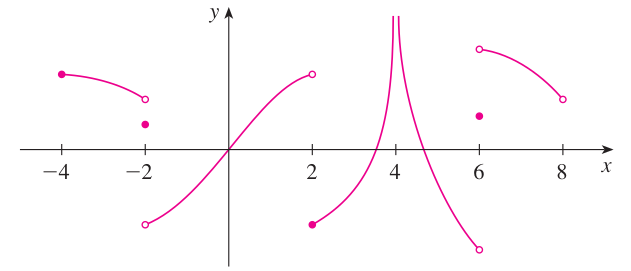
(a). 각 함수의 불연속점과 그 이유를 말하여라.
(b). 각 함수의 연속인 구간을 작성하라.
(a). 각 함수의 불연속점을 작성하라.
1). $y = f(x)$
$x = -4$ : $\lim_{x \rightarrow -4} f(x) \neq f(-4)$
$x = -2$ : $\lim_{x \rightarrow -2^{-}} f(x) \neq \lim_{x \rightarrow -2^{+}} f(x)$
$x = 2$ : $\lim_{x \rightarrow 2^{-}} f(x) \neq \lim_{x \rightarrow 2^{+}} f(x)$
$x = 4$ : $\lim_{x \rightarrow 4^{-}} f(x) = -\infty$로 발산
2). $y = g(x)$
$x = -2$ : $\lim_{x \rightarrow -2^{-}} f(x) \neq \lim_{x \rightarrow -2^{+}} f(x)$
$x = 2$ : $\lim_{x \rightarrow 2^{-}} f(x) \neq \lim_{x \rightarrow 2^{+}} f(x)$
$x = 6$ : $\lim_{x \rightarrow 6^{-}} f(x) \neq \lim_{x \rightarrow 6^{+}} f(x)$
(b). 각 함수의 연속인 구간을 작성하라.
1). $y = f(x) \rightarrow (-\infty, -4) \cup (-4, -2) \cup (-2, 2) \cup (2, 4) \cup (4, \infty)$
2). $y = g(x) \rightarrow \cup (-4, -2) \cup (-2, 2) \cup (2, 4) \cup (4, 6) \cup (6, 8)$
연습문제2. 함수 $f$와 $g$가 연속이고 $f(3) = 5$와 $\lim_{x \rightarrow 3} \left[ 2f(x) - g(x) \right] = 4$를 만족한다고 할 때 $g(3)$을 구하여라.
두 함수 $f$와 $g$가 모두 연속함수이기 때문에 $\lim_{x \rightarrow 3} f(x) = f(3)$이고 $\lim_{x \rightarrow 3} g(x) = g(3)$으로 극한값이 존재한다. 따라서, 미적분학 - 극한 법칙을 이용한 극한 계산하기를 이용해서 극한을 정리한다.
$$\begin{align*} \lim_{x \rightarrow 3} \left[ 2f(x) - g(x) \right] &= 2\lim_{x \rightarrow 3} f(x) - \lim_{x \rightarrow 3} g(x) \\ &= 2 \cdot f(3) - g(3) \\ &= 2 \cdot 5 - g(3) = 4 \end{align*}$$
따라서, $g(3) = 6$이다.
연습문제3. 극한과 연속의 정의 및 성질을 이용해서 아래의 함수들의 연속성을 증명하라.
(a). 점 $x = 4$에서 $f(x) = x^{2} + \sqrt{7 - x}$의 연속성
(b). 점 $x = -1$에서 $f(x) = (x + 2x^{3})^{4}$의 연속성
(c). 점 $x = 1$에서 $f(x) = \frac{2t - 3t^{4}}{1 + t^{3}}$의 연속성
(d). 구간 $(2, \infty)$에서 $f(x) = \frac{2x + 3}{x - 2}$의 연속성
(e). 구간 $(-\infty, 3]$에서 $f(x) = 2\sqrt{3 - x}$의 연속성
(a). 점 $x = 4$에서 $f(x) = x^{2} + \sqrt{7 - x}$의 연속성
$g(x) = x^{2}, h(x) = \sqrt{7 - x}$라고 하자. $g$는 다향함수이고 $h$는 무리함수이기 때문에 정리 1에 의해 두 함수 $g$와 $h$는 각각 $\text{dom}(g) = \mathbb{R}$과 $\text{dom}(h) = (-\infty, 7]$에서 연속이다. 따라서, $f = g + h$ 는 구간 $\text{dom}(f) = \text{dom}(g) \cap \text{dom}(h) = (-\infty, 7]$에서 연속이므로 함수 $f$는 점 $x = 4$에서 연속이다.
(b). 점 $x = -1$에서 $f(x) = (x + 2x^{3})^{4}$의 연속성
$g(x) = x^{4}, h(x) = x + 2x^{3}$라고 하자. $g$와 $h$는 다향함수이기 때문에 정리 1에 의해 두 함수 $g$와 $h$는 $\text{dom}(g) = \text{dom}(h) = \mathbb{R}$에서 연속이다. 따라서, $f = g \circ h$ 는 정리3에 의해 구간 $\text{dom}(f) = \text{dom}(h) = \mathbb{R}$에서 연속이므로 함수 $f$는 점 $x = -1$에서 연속이다.
(c). 점 $x = 1$에서 $f(x) = \frac{2t - 3t^{4}}{1 + t^{3}}$의 연속성
$f$ 는 유리함수이므로 정리1에 의해 구간 $\text{dom}(f) = \{x \in \mathbb{R} | x \neq -1\}$에서 연속이므로 함수 $f$는 점 $x = 1$에서 연속이다.
(d). 구간 $(2, \infty)$에서 $f(x) = \frac{2x + 3}{x - 2}$의 연속성
$f$ 는 유리함수이므로 정리1에 의해 구간 $\text{dom}(f) = \{x \in \mathbb{R} | x \neq 2\}$에서 연속이므로 함수 $f$는 구간 $(2, \infty)$에서 연속이다.
(e). 구간 $(-\infty, 3]$에서 $f(x) = 2\sqrt{3 - x}$의 연속성
$f$ 는 무리함수이므로 정리1에 의해 구간 $\text{dom}(f) = (-\infty, 3]$에서 연속이다.
연습문제4. 다음 함수와 점이 주어졌을 때 해당 점에서 주어진 함수가 불연속인 이유를 설명하라.
(a). $f(x) = \ln(x - 2), x = 2$
(b). $f(x) = \begin{cases} \frac{1}{x - 1} &\text{ if } x \neq 1 \\ 2 &\text{ if } x = 1\end{cases}, x = 1$
(c). $f(x) = \begin{cases} e^{x} &\text{ if } x < 0 \\ x^{2} &\text{ if } x \ge 1\end{cases}, x = 0$
(d). $f(x) = \begin{cases} \frac{x^{2} - x}{x^{2} - 1} &\text{ if } x \neq 1 \\ 1 &\text{ if } x = 1\end{cases}, x = 1$
(e). $f(x) = \begin{cases} \cos(x) &\text{ if } x < 0 \\ 0 &\text{ if } x = 0 \\ 1 - x^{2} &\text{ if } x > 0 \end{cases}, x = 0$
(f). $f(x) = \begin{cases} \frac{2x^{2} - 5x - 3}{x - 3} &\text{ if } x \neq 3 \\ 6 &\text{ if } x = 3\end{cases}, x = 3$
(a). $f(x) = \ln(x - 2), x = 2$
함수 $f$는 점 $x = 2$에서 정의되지 않으므로 $x = 2$에서 함수 $f$는 불연속이다.
(b). $f(x) = \begin{cases} \frac{1}{x - 1} &\text{ if } x \neq 1 \\ 2 &\text{ if } x = 1\end{cases}, x = 1$
1). $\lim_{x \rightarrow 1^{-}} f(x) = \lim_{x \rightarrow 1^{-}} \frac{1}{x - 1} = -\infty$
2). $\lim_{x \rightarrow 1^{+}} f(x) = \lim_{x \rightarrow 1^{+}} \frac{1}{x - 1} = \infty$
$\lim_{x \rightarrow 1} f(x)$가 존재하지 않기 때문에 점 $x = 1$에서 함수 $f$는 불연속이다.
(c). $f(x) = \begin{cases} e^{x} &\text{ if } x < 0 \\ x^{2} &\text{ if } x \ge 1\end{cases}, x = 0$
1). $\lim_{x \rightarrow 0^{-}} f(x) = \lim_{x \rightarrow 0^{-}} e^{x} = 1$
2). $\lim_{x \rightarrow 0^{+}} f(x) = \lim_{x \rightarrow 0^{+}} x^{2} = 0$
$\lim_{x \rightarrow 1} f(x)$가 존재하지 않기 때문에 점 $x = 1$에서 함수 $f$는 불연속이다.
(d). $f(x) = \begin{cases} \frac{x^{2} - x}{x^{2} - 1} &\text{ if } x \neq 1 \\ 1 &\text{ if } x = 1\end{cases}, x = 1$
1). $\lim_{x \rightarrow 1^{-}} f(x) = \lim_{x \rightarrow 1^{-}} \frac{x^{2} - x}{x^{2} - 1} = \lim_{x \rightarrow 1^{-}} \frac{x(x - 1)}{(x + 1)(x - 1)} = \lim_{x \rightarrow 1^{-}} \frac{x}{x + 1} = \frac{1}{2}$
2). $\lim_{x \rightarrow 1^{+}} f(x) = \lim_{x \rightarrow 1^{+}} \frac{x^{2} - x}{x^{2} - 1} = \lim_{x \rightarrow 1^{+}} \frac{x(x - 1)}{(x + 1)(x - 1)} = \lim_{x \rightarrow 1^{+}} \frac{x}{x + 1} = \frac{1}{2}$
$\lim_{x \rightarrow 1} f(x) = \frac{1}{2} \neq 1 = f(1)$이기 때문에 점 $x = 1$에서 함수 $f$는 불연속이다.
(e). $f(x) = \begin{cases} \cos(x) &\text{ if } x < 0 \\ 0 &\text{ if } x = 0 \\ 1 - x^{2} &\text{ if } x > 0 \end{cases}, x = 0$
1). $\lim_{x \rightarrow 0^{-}} f(x) = \lim_{x \rightarrow 0^{-}} \cos(x) = 1$
2). $\lim_{x \rightarrow 0^{+}} f(x) = \lim_{x \rightarrow 0^{+}} \left[ 1 - x^{2} \right] = 1$
$\lim_{x \rightarrow 0} f(x) = 1 \neq 0 = f(0)$이기 때문에 점 $x = 0$에서 함수 $f$는 불연속이다.
(f). $f(x) = \begin{cases} \frac{2x^{2} - 5x - 3}{x - 3} &\text{ if } x \neq 3 \\ 6 &\text{ if } x = 3\end{cases}, x = 3$
1). $\lim_{x \rightarrow 3^{-}} f(x) = \lim_{x \rightarrow 3^{-}} \frac{2x^{2} - 5x - 3}{x - 3} = \lim_{x \rightarrow 3^{-}} \frac{(x - 3)(2x + 1)}{(x - 3)} = \lim_{x \rightarrow 3^{-}} (2x + 1) = 7$
2). $\lim_{x \rightarrow 3^{+}} f(x) = \lim_{x \rightarrow 3^{+}} \frac{2x^{2} - 5x - 3}{x - 3} = \lim_{x \rightarrow 3^{+}} \frac{(x - 3)(2x + 1)}{(x - 3)} = \lim_{x \rightarrow 3^{+}} (2x + 1) = 7$
$\lim_{x \rightarrow 3} f(x) = 7 \neq 6 = f(3)$이기 때문에 점 $x = 3$에서 함수 $f$는 불연속이다.
연습문제5. 주어진 함수의 연속성을 이용해서 주어진 극한을 계산하라.
(a). $\lim_{x \rightarrow 4} \frac{5 + \sqrt{x}}{\sqrt{5 + x}}$
(b). $\lim_{x \rightarrow \pi} \sin(x +\sin(x))$
(c). $\lim_{x \rightarrow 1} e^{x^{2} - x}$
(d). $\lim_{x \rightarrow 2} \arctan \left( \frac{x^{2} - 4}{3x^{2} - 6x} \right)$
(a). $\lim_{x \rightarrow 4} \frac{5 + \sqrt{x}}{\sqrt{5 + x}}$
$f(x) = \frac{5 +\sqrt{x}}{\sqrt{5 + x}}$라고 하자. 함수 $f$가 연속이므로 $\lim_{x \rightarrow 4} f(x) = f(4) = \frac{7}{3}$이다.
(b). $\lim_{x \rightarrow \pi} \sin(x +\sin(x))$
$f(x) = \sin(x + \sin(x))$라고 하자. 함수 $f$가 연속이므로 $\lim_{x \rightarrow \pi} f(x) = f(\pi) = 0$이다.
(c). $\lim_{x \rightarrow 1} e^{x^{2} - x}$
$f(x) = e^{x^{2} - 1}$라고 하자. 함수 $f$가 연속이므로 $\lim_{x \rightarrow 1} f(x) = f(1) = 1$이다.
(d). $\lim_{x \rightarrow 2} \arctan \left( \frac{x^{2} - 4}{3x^{2} - 6x} \right)$
$f(x) = \arctan \left( \frac{x^{2} - 4}{3x^{2} - 6x} \right)$라고 하자. 함수 $f$가 연속이므로 $\lim_{x \rightarrow 2} f(x) = f(2) = \arctan \left( \frac{2}{3} \right)$이다.
연습문제6. $f(x) = \begin{cases} cx^{2} + 2x &\text{ if } x < 2 \\ x^{3} - cx &\text{ if } x \le 2 \end{cases}$가 주어졌다고 하자. 함수 $f$가 $(-\infty, \infty)$에서 연속이 되기 위한 상수 $c$를 구하시오.
연속함수의 정의에 의해 함수 $f$가 연속이 되기 위해서는 $x = 2$에서 좌극한, 우극한, 그리고 함숫값이 같아야 한다.
1). 좌극한 : $\lim_{x \rightarrow 2^{-}} f(x) = \lim_{x \rightarrow 2^{-}} (cx^{2} + 2x) = 4c + 4$
2). 우극한 : $\lim_{x \rightarrow 2^{+}} f(x) = \lim_{x \rightarrow 2^{+}} (x^{3} - cx) = 8 - 2c$
따라서, $4c + 4 = 8 - 2c$를 만족하는 $c = \frac{2}{3}$이 유일하다.
연습문제7. $f(x) = \begin{cases} \frac{x^{2} - 4}{x - 2} &\text{ if } x < 2 \\ ax^{2} - bx + 3 &\text{ if } 2 < x < 3 \\ 2x - a + b &\text{ if } x \ge 3 \end{cases}$가 주어졌다고 하자. 함수 $f$가 $(-\infty, \infty)$에서 연속이 되기 위한 상수 $a$와 $b$를 구하시오.
연속함수의 정의에 의해 함수 $f$가 연속이 되기 위해서는 $x = 2$와 $x = 3$에서 좌극한, 우극한, 그리고 함숫값이 같아야 한다.
1 - a). 좌극한 : $\lim_{x \rightarrow 2^{-}} f(x) = \lim_{x \rightarrow 2^{-}} \frac{x^{2} - 4}{x - 2} = \lim_{x \rightarrow 2^{-}} (x + 2) = 4$
1 - b). 우극한 : $\lim_{x \rightarrow 2^{+}} f(x) = \lim_{x \rightarrow 2^{+}} (ax^{2} - bx + 3) = 4a - 2b + 3$
2 - a). 좌극한 : $\lim_{x \rightarrow 3^{-}} f(x) = \lim_{x \rightarrow 3^{-}} (ax^{2} - bx + 3) = 9a - 3b + 3$
2 - b). 우극한 : $\lim_{x \rightarrow 3^{+}} f(x) = \lim_{x \rightarrow 3^{+}} (2x - a + b) = 6 - a + b$
따라서, 1차 연립방정식 $\begin{cases} &4a - 2b + 3 = 4 \\ &9a - 3b + 3 = 6 - a + b \end{cases}$를 만족하는 $a = \frac{1}{2}$와 $b = \frac{1}{2}$가 유일하다.
연습문제8. 주어진 방정식이 특정 구간에서 해를 가짐을 중간값 정리를 이용해서 증명하라.
(a). $x^{4} + x - 3 = 0, (1, 2)$
(b). $\sqrt[3]{x} = 1 - x, (0, 1)$
(c). $\cos(x) = x, (0, 1)$
(d). $\ln(x) = e^{x}, (1, 2)$
(a). $x^{4} + x - 3 = 0, (1, 2)$
$f(x) = x^{4} + x - 3$이라고 하자. $f(1) = -1 < 0 < 15 = f(2)$이고 함수 $f$는 연속함수이므로 정리4(IVT)에 의해 $f(c) = 0$를 만족하는 $c$가 열린 구간 $(1, 2)$에서 적어도 하나 존재한다.
(b). $\sqrt[3]{x} = 1 - x, (0, 1)$
$f(x) = \sqrt[3]{x} + x - 1$이라고 하자. $f(0) = -1 < 0 < 1 = f(1)$이고 함수 $f$는 연속함수이므로 정리4(IVT)에 의해 $f(c) = 0$를 만족하는 $c$가 열린 구간 $(0, 1)$에서 적어도 하나 존재한다.
(c). $\cos(x) = x, (0, 1)$
$f(x) = \cos{x} - x$이라고 하자. $f(1) < 0 < 1 = f(0)$이고 함수 $f$는 연속함수이므로 정리4(IVT)에 의해 $f(c) = 0$를 만족하는 $c$가 열린 구간 $(0, 1)$에서 적어도 하나 존재한다.
(d). $\ln(x) = e^{x}, (1, 2)$
$f(x) = \ln{x} - e^{x}$이라고 하자. $f(1) = -e^{-1} < 0 < \ln(2) - e^{-2} = f(2)$이고 함수 $f$는 연속함수이므로 정리4(IVT)에 의해 $f(c) = 0$를 만족하는 $c$가 열린 구간 $(1, 2)$에서 적어도 하나 존재한다.
연습문제9. $f(x) = \begin{cases} 0 &\text{ if } x \in \mathbb{Q} \\ 1 &\text{ if } x \in \mathbb{I} \end{cases}$라고 하자. 함수 $f$가 연속인 지점이 존재하는 지 확인하시오.
함수 $f$가 $x = c$에서 연속이라고 하자. 따라서, 연속의 정의에 의해 $\lim_{x \rightarrow c} f(x) = f(c)$를 만족한다. 극한의 정의를 적용하기 위해 $\epsilon = \frac{1}{2}$라고 하자. $|x - c| < \delta$이면 $|f(x) - f(c)| < \frac{1}{2}$를 만족하는 $\delta > 0$가 존재한다.
1). 무리수 $a \in (c - \delta, c + \delta) \cap \mathbb{I}$를 선택하는 경우
$$\begin{align*} &|f(a) - f(c)| = |1 - f(c)| < \frac{1}{2} \\ \Rightarrow& -\frac{1}{2} < 1 - f(c) < \frac{1}{2} \\ \Rightarrow& -\frac{3}{2} < -f(c) < -\frac{1}{2} \\ \Rightarrow& \frac{1}{2} < f(c) < \frac{3}{2} \end{align*}$$
2). 유리수 $a \in (c - \delta, c + \delta) \cap \mathbb{Q}$를 선택하는 경우
$$\begin{align*} &|f(a) - f(c)| = |f(c)| < \frac{1}{2} \\ \Rightarrow& -\frac{1}{2} < f(c) < \frac{1}{2} \end{align*}$$
여기서, 두 함수값의 차이가 절대 작아질 수 없음을 증명하면 귀류법에 의해 모순이 되어 함수 $f$는 어떠한 지점에서도 연속이 아님이 증명된다.
$$\begin{align*} |f(a) - f(b)| &= |(f(a) - f(c)) + (f(c) - f(b))| \\ &\le |f(a) - f(c)| + |f(b) - f(c)| \\ &= \frac{1}{2} + \frac{1}{2} = 1 \end{align*}$$
즉, 유리수와 무리수를 선택했을 때 두 함숫값의 차이가 좁혀지지 않으므로 함수 $f$는 어떠한 점에서도 연속이 아니다.
연습문제10. 방정식 $\frac{a}{x^{3} + 2x^{2} - 1} + \frac{b}{x^{3} + x - 2} = 0$이 열린 구간 $(-1, 1)$ 사이에서 적어도 하나의 근이 있음을 증명하라. 이때, $a$와 $b$는 양수이다.
함수 $\frac{a}{x^{3} + 2x^{2} - 1} + \frac{b}{x^{3} + x - 2} = 0$라고 하자.
$$\begin{align*} f(x) &= \frac{a}{x^{3} + 2x^{2} - 1} + \frac{b}{x^{3} + x - 2} \\ &= \frac{a}{(x + 1)(x^{2} + x - 1)} + \frac{b}{(x - 1)(x^{2} + x + 2)} \\ &= \frac{a(x - 1)(x^{2} + x + 2) + b(x + 1)(x^{2} + x + 1)}{(x + 1)(x^{2} + x - 1)(x - 1)(x^{2} + x + 2)} \end{align*}$$
이때, $f(x) = 0$이 되는 것은 $f$의 분자가 0이 되는 것과 동치이다. $g(x) = a(x - 1)(x^{2} + x + 2) + b(x + 1)(x^{2} + x + 1)$이라고 하면 $g(-1) = -4a < 0 < 6b = g(1)$이고 함수 $g$는 연속함수이므로 정리4(IVT)에 의해 열린 구간 $(-1, 1)$에서 $g(c) = 0 \leftrightarrow f(c) = 0$을 만족하는 $x = c$가 적어도 하나 존재한다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.08.08 : 전체적인 스타일 수정
22.08.08 : 연습문제1-5 추가
22.08.09 : 연습문제6-10 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 미분 개요 (0) | 2021.10.22 |
|---|---|
| 미적분학 - 무한대 극한 (0) | 2021.09.07 |
| 미적분학 - 정확한 극한의 정의 (0) | 2021.08.25 |
| 미적분학 - 극한 법칙을 이용한 극한 계산하기 (0) | 2021.08.20 |
| 미적분학 - 함수의 극한 (0) | 2021.08.17 |
안녕하세요. 지난 포스팅의 미적분학- 극한의 정확한 정의에서는 좌극한, 우극한의 정의와 함께 무한대로 발산하는 경우의 정의까지 알아보았습니다. 오늘은 극한을 통해 정의되는 새로운 함수의 종류인 연속함수 (continuous function)에 대해서 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
정의1. 연속함수 (Continuous functions)와 불연속 함수 (Discontinuous function)
함수 f가 limx→af(x)=f(a)라면 f를 x=a에서의 연속함수 (continuous function)이라고 한다. 만약, limx→af(x)≠f(a)라면 f를 x=a에서의 불연속 함수 (discontinuous function)이라고 한다.
설명
연속함수는 아마 다들 어느정도 이해하실거라고 생각합니다. 아마도 대부분이 연속함수란 정의역에서 함수가 끊기지 않고 모두 연결되어있는 함수로 생각하실 겁니다. 이 정도도 사실은 충분하지만 어떻게 하면 좀 더 수학적으로 정의해 볼 수 있을까요? 이를 위해 저희는 "함수가 끊어지지 않는다."라는 특징에 집중할 필요가 있습니다.

일단, 함수가 x=a에서 "끊겼다."라는 것은 함수가 연결되어 있지 않다는 의미이고 이는 위의 그림과 같이 세 가지 케이스로 나누어서 생각해볼 수 있습니다. 먼저, 가장 왼쪽의 x=1처럼 f(x)가 x=a에서 정의가 되지 않는 경우입니다. 이 경우에는 x=a에서 f(x)가 그냥 구멍이 뚫려있습니다. 다음으로 생각해볼 수 있는 것은 f(x)가 x=a에서 정의는 되어있지만 끊겨있는 경우가 있을까요? 이를 위해 극한이 필요합니다. 다시 상기하면 극한이란 x=≠a이지만 x가 a로 한없이 가까워질 때 얻을 수 있는 값이 됩니다. 그런데 만약 극한값이 존재하지 않는다면 가운데의 x=3과 같이 될 것 입니다. 마지막으로는 x=5와 같이 극한값은 존재하지만 함숫값과 다른 경우도 문제가 됩니다. 따라서 이러한 조건을 모두 피하는 것이 바로 "limx→af(x)=f(a)"이고 이 조건을 만족하면 함수 f(x)를 연속함수라고 합니다.

위 그림은 연속 함수를 그림으로 표현한 것 입니다. x=a를 중심으로 양쪽에서 접근했을 때 그에 대응되는 함숫값 역시 f(a)에 무한히 가까워지게 될 것 입니다. 지금까지 본 것은 "하나의 점"에서만 연속 조건을 만족하는 경우입니다. 그리고 이러한 점들을 모아서 구간을 만들면 함수 f는 구간에서 연속 함수라고 부를 수 있습니다. 예를 들어 f(x)=x 함수는 모든 실수점에서 연속함수이기 때문에 R에서 연속함수라고 말할 수 있습니다. 즉, 저희는 지난 포스팅의 미적분학 - 정확한 극한의 정의에서 보았던 엡실론-델타 논법을 다시 한번 적용해야하는 것을 알 수 있습니다.
정의1-1. 연속함수와 엡실론-델타 논법
함수 f가 임의의 양수 ϵ>0에 대해서 |x−a|<δ일 때 |f(x)−f(a)|<ϵ을 만족하는 δ>0가 존재하면 함수 f는 x=a에서 연속이라고 한다.
연속함수에는 저희가 이후에 함수를 좀 더 쉽게 다룰 수 있도록 도와주는 유용한 성질들이 있습니다. 차근차근 살펴보도록 하죠.
정리1. 연속함수의 판별
- 만약 함수 f와 g가 x=a에서 연속함수이고 c가 상수라면 f±g,cf,fg,fg는 연속함수이다.
- 임의의 다항함수는 모든 실수 R에서 연속함수이다.
- 다항함수, 유리함수, 제곱근함수, 삼각함수, 역삼각함수, 지수함수, 로그함수 모두 정의된 정의역에서 연속함수이다.
정리2.
만약 f가 x=b에서 연속이고 limx→ag(x)=b이면 limx→f(g(x))=f(b)이다.
limx→af(g(x))=f(limx→ag(x))
설명
정리2의 증명은 간단합니다. 연속와 합성함수의 정의를 차근차근 적용해보면 됩니다. 먼적, 함수 f가 x=b에서 연속함수이기 때문에 임의의 양의 실수 ϵ>0에 대해서 |x−b|<δ1일 때 |f(x)−f(b)|<ϵ을 만족하는 δ1>0가 존재합니다. 또한, limx→ag(x)=b이기 때문에 극한의 정의에 의해 |x−a|<δ2일 때 |g(x)−g(a)|<δ1을 만족하는 δ2>0가 존재하죠.
δ=min{δ1,δ2}라고 하도록 하겠습니다. |x−a|<δ일 때 |g(x)−b|<δ1을 만족하고 g(x)=y라고 할 때 |f(y)−f(b)|<ϵ을 만족하기 때문에 limx→af(g(x))=f(b)입니다.
정리3. 합성함수의 연속성
함수 g가 x=a에서 연속이고 함수 f가 x=g(a)에서 연속이라고 하면 (f∘g)(x)=f(g(x))로 정의되는 합성함수 f∘g는 x=a에서 연속이다.
설명
정리3을 증명해보도록 하겠습니다. 함수 g가 점 x=a에서 연속이기 때문에 limx→ag(x)=g(a)입니다. 또한, 함수 f가 점 x=b=g(a)에서 연속이기 때문에 limx→af(g(x))=f(g(a))가 되죠. 이것은 h=f∘g라고 했을 때 함수 h가 점 x=a에서 연속인 것과 동일한 의미이므로 f∘g는 점 x=a에서 연속이 됩니다.
예제1.limx→1arcsin(1−√x1−x)의 값을 구하여라.
limx→1arcsin(1−√x1−x)=arcsinlimx→1(1−√x1−x)를 만족한다.
limx→1arcsin(1−√x1−x)=arcsinlimx→1(1−√x1−x)=arcsinlimx→1(1−√x(1−√x)(1+√x))=arcsinlimx→1(11+√x)=arcsin12=π6
정리4. 중간값 정리 (Intermediate Value Theorem; IVT)
f가 닫힌 구간 [a,b]에서 연속이고 N을 f(a)와 f(b) 사이의 임의의 숫자라고 가정하면(이때, f(a)≠f(b)이다.) f(c)=N을 만족하는 c가 열린 구간 (a,b)에 존재한다.
설명

중간값 정리를 그림으로 그려보면 위와 같습니다. 아주 명확한 그림이죠. 중간값 정리는 이후에 다양한 증명에서 활용되기 때문에 꼭 알아두셔야하는 정리 중 하나입니다.
특히,IVT가 가장 많이 활용되는 증명 중 하나는 특정 구간에서 해의 존재성을 판단하는 것입니다. 예를 들어, f(a)<0이고 f(b)>0인 연속함수 f가 주어졌을 때 IVT에 의해서 함수 f는 열린 구간 (a,b)에서 f(c)=0을 만족하는 x=c를 찾을 수 있다는 것을 알려줍니다. 이와 같은 방법으로 앞으로 다양한 문제들을 풀 수 있습니다.
연습문제1. 아래의 두 그래프에 대해서 물음에 답하여라.


(a). 각 함수의 불연속점과 그 이유를 말하여라.
(b). 각 함수의 연속인 구간을 작성하라.
(a). 각 함수의 불연속점을 작성하라.
1). y=f(x)
x=−4 : limx→−4f(x)≠f(−4)
x=−2 : limx→−2−f(x)≠limx→−2+f(x)
x=2 : limx→2−f(x)≠limx→2+f(x)
x=4 : limx→4−f(x)=−∞로 발산
2). y=g(x)
x=−2 : limx→−2−f(x)≠limx→−2+f(x)
x=2 : limx→2−f(x)≠limx→2+f(x)
x=6 : limx→6−f(x)≠limx→6+f(x)
(b). 각 함수의 연속인 구간을 작성하라.
1). y=f(x)→(−∞,−4)∪(−4,−2)∪(−2,2)∪(2,4)∪(4,∞)
2). y=g(x)→∪(−4,−2)∪(−2,2)∪(2,4)∪(4,6)∪(6,8)
연습문제2. 함수 f와 g가 연속이고 f(3)=5와 limx→3[2f(x)−g(x)]=4를 만족한다고 할 때 g(3)을 구하여라.
두 함수 f와 g가 모두 연속함수이기 때문에 limx→3f(x)=f(3)이고 limx→3g(x)=g(3)으로 극한값이 존재한다. 따라서, 미적분학 - 극한 법칙을 이용한 극한 계산하기를 이용해서 극한을 정리한다.
limx→3[2f(x)−g(x)]=2limx→3f(x)−limx→3g(x)=2⋅f(3)−g(3)=2⋅5−g(3)=4
따라서, g(3)=6이다.
연습문제3. 극한과 연속의 정의 및 성질을 이용해서 아래의 함수들의 연속성을 증명하라.
(a). 점 x=4에서 f(x)=x2+√7−x의 연속성
(b). 점 x=−1에서 f(x)=(x+2x3)4의 연속성
(c). 점 x=1에서 f(x)=2t−3t41+t3의 연속성
(d). 구간 (2,∞)에서 f(x)=2x+3x−2의 연속성
(e). 구간 (−∞,3]에서 f(x)=2√3−x의 연속성
(a). 점 x=4에서 f(x)=x2+√7−x의 연속성
g(x)=x2,h(x)=√7−x라고 하자. g는 다향함수이고 h는 무리함수이기 때문에 정리 1에 의해 두 함수 g와 h는 각각 dom(g)=R과 dom(h)=(−∞,7]에서 연속이다. 따라서, f=g+h 는 구간 dom(f)=dom(g)∩dom(h)=(−∞,7]에서 연속이므로 함수 f는 점 x=4에서 연속이다.
(b). 점 x=−1에서 f(x)=(x+2x3)4의 연속성
g(x)=x4,h(x)=x+2x3라고 하자. g와 h는 다향함수이기 때문에 정리 1에 의해 두 함수 g와 h는 dom(g)=dom(h)=R에서 연속이다. 따라서, f=g∘h 는 정리3에 의해 구간 dom(f)=dom(h)=R에서 연속이므로 함수 f는 점 x=−1에서 연속이다.
(c). 점 x=1에서 f(x)=2t−3t41+t3의 연속성
f 는 유리함수이므로 정리1에 의해 구간 dom(f)={x∈R|x≠−1}에서 연속이므로 함수 f는 점 x=1에서 연속이다.
(d). 구간 (2,∞)에서 f(x)=2x+3x−2의 연속성
f 는 유리함수이므로 정리1에 의해 구간 dom(f)={x∈R|x≠2}에서 연속이므로 함수 f는 구간 (2,∞)에서 연속이다.
(e). 구간 (−∞,3]에서 f(x)=2√3−x의 연속성
f 는 무리함수이므로 정리1에 의해 구간 dom(f)=(−∞,3]에서 연속이다.
연습문제4. 다음 함수와 점이 주어졌을 때 해당 점에서 주어진 함수가 불연속인 이유를 설명하라.
(a). f(x)=ln(x−2),x=2
(b). f(x)={1x−1 if x≠12 if x=1,x=1
(c). f(x)={ex if x<0x2 if x≥1,x=0
(d). f(x)={x2−xx2−1 if x≠11 if x=1,x=1
(e). f(x)={cos(x) if x<00 if x=01−x2 if x>0,x=0
(f). f(x)={2x2−5x−3x−3 if x≠36 if x=3,x=3
(a). f(x)=ln(x−2),x=2
함수 f는 점 x=2에서 정의되지 않으므로 x=2에서 함수 f는 불연속이다.
(b). f(x)={1x−1 if x≠12 if x=1,x=1
1). limx→1−f(x)=limx→1−1x−1=−∞
2). limx→1+f(x)=limx→1+1x−1=∞
limx→1f(x)가 존재하지 않기 때문에 점 x=1에서 함수 f는 불연속이다.
(c). f(x)={ex if x<0x2 if x≥1,x=0
1). limx→0−f(x)=limx→0−ex=1
2). limx→0+f(x)=limx→0+x2=0
limx→1f(x)가 존재하지 않기 때문에 점 x=1에서 함수 f는 불연속이다.
(d). f(x)={x2−xx2−1 if x≠11 if x=1,x=1
1). limx→1−f(x)=limx→1−x2−xx2−1=limx→1−x(x−1)(x+1)(x−1)=limx→1−xx+1=12
2). limx→1+f(x)=limx→1+x2−xx2−1=limx→1+x(x−1)(x+1)(x−1)=limx→1+xx+1=12
limx→1f(x)=12≠1=f(1)이기 때문에 점 x=1에서 함수 f는 불연속이다.
(e). f(x)={cos(x) if x<00 if x=01−x2 if x>0,x=0
1). limx→0−f(x)=limx→0−cos(x)=1
2). limx→0+f(x)=limx→0+[1−x2]=1
limx→0f(x)=1≠0=f(0)이기 때문에 점 x=0에서 함수 f는 불연속이다.
(f). f(x)={2x2−5x−3x−3 if x≠36 if x=3,x=3
1). limx→3−f(x)=limx→3−2x2−5x−3x−3=limx→3−(x−3)(2x+1)(x−3)=limx→3−(2x+1)=7
2). limx→3+f(x)=limx→3+2x2−5x−3x−3=limx→3+(x−3)(2x+1)(x−3)=limx→3+(2x+1)=7
limx→3f(x)=7≠6=f(3)이기 때문에 점 x=3에서 함수 f는 불연속이다.
연습문제5. 주어진 함수의 연속성을 이용해서 주어진 극한을 계산하라.
(a). limx→45+√x√5+x
(b). limx→πsin(x+sin(x))
(c). limx→1ex2−x
(d). limx→2arctan(x2−43x2−6x)
(a). limx→45+√x√5+x
f(x)=5+√x√5+x라고 하자. 함수 f가 연속이므로 limx→4f(x)=f(4)=73이다.
(b). limx→πsin(x+sin(x))
f(x)=sin(x+sin(x))라고 하자. 함수 f가 연속이므로 limx→πf(x)=f(π)=0이다.
(c). limx→1ex2−x
f(x)=ex2−1라고 하자. 함수 f가 연속이므로 limx→1f(x)=f(1)=1이다.
(d). limx→2arctan(x2−43x2−6x)
f(x)=arctan(x2−43x2−6x)라고 하자. 함수 f가 연속이므로 limx→2f(x)=f(2)=arctan(23)이다.
연습문제6. f(x)={cx2+2x if x<2x3−cx if x≤2가 주어졌다고 하자. 함수 f가 (−∞,∞)에서 연속이 되기 위한 상수 c를 구하시오.
연속함수의 정의에 의해 함수 f가 연속이 되기 위해서는 x=2에서 좌극한, 우극한, 그리고 함숫값이 같아야 한다.
1). 좌극한 : limx→2−f(x)=limx→2−(cx2+2x)=4c+4
2). 우극한 : limx→2+f(x)=limx→2+(x3−cx)=8−2c
따라서, 4c+4=8−2c를 만족하는 c=23이 유일하다.
연습문제7. f(x)={x2−4x−2 if x<2ax2−bx+3 if 2<x<32x−a+b if x≥3가 주어졌다고 하자. 함수 f가 (−∞,∞)에서 연속이 되기 위한 상수 a와 b를 구하시오.
연속함수의 정의에 의해 함수 f가 연속이 되기 위해서는 x=2와 x=3에서 좌극한, 우극한, 그리고 함숫값이 같아야 한다.
1 - a). 좌극한 : limx→2−f(x)=limx→2−x2−4x−2=limx→2−(x+2)=4
1 - b). 우극한 : limx→2+f(x)=limx→2+(ax2−bx+3)=4a−2b+3
2 - a). 좌극한 : limx→3−f(x)=limx→3−(ax2−bx+3)=9a−3b+3
2 - b). 우극한 : limx→3+f(x)=limx→3+(2x−a+b)=6−a+b
따라서, 1차 연립방정식 {4a−2b+3=49a−3b+3=6−a+b를 만족하는 a=12와 b=12가 유일하다.
연습문제8. 주어진 방정식이 특정 구간에서 해를 가짐을 중간값 정리를 이용해서 증명하라.
(a). x4+x−3=0,(1,2)
(b). 3√x=1−x,(0,1)
(c). cos(x)=x,(0,1)
(d). ln(x)=ex,(1,2)
(a). x4+x−3=0,(1,2)
f(x)=x4+x−3이라고 하자. f(1)=−1<0<15=f(2)이고 함수 f는 연속함수이므로 정리4(IVT)에 의해 f(c)=0를 만족하는 c가 열린 구간 (1,2)에서 적어도 하나 존재한다.
(b). 3√x=1−x,(0,1)
f(x)=3√x+x−1이라고 하자. f(0)=−1<0<1=f(1)이고 함수 f는 연속함수이므로 정리4(IVT)에 의해 f(c)=0를 만족하는 c가 열린 구간 (0,1)에서 적어도 하나 존재한다.
(c). cos(x)=x,(0,1)
f(x)=cosx−x이라고 하자. f(1)<0<1=f(0)이고 함수 f는 연속함수이므로 정리4(IVT)에 의해 f(c)=0를 만족하는 c가 열린 구간 (0,1)에서 적어도 하나 존재한다.
(d). ln(x)=ex,(1,2)
f(x)=lnx−ex이라고 하자. f(1)=−e−1<0<ln(2)−e−2=f(2)이고 함수 f는 연속함수이므로 정리4(IVT)에 의해 f(c)=0를 만족하는 c가 열린 구간 (1,2)에서 적어도 하나 존재한다.
연습문제9. f(x)={0 if x∈Q1 if x∈I라고 하자. 함수 f가 연속인 지점이 존재하는 지 확인하시오.
함수 f가 x=c에서 연속이라고 하자. 따라서, 연속의 정의에 의해 limx→cf(x)=f(c)를 만족한다. 극한의 정의를 적용하기 위해 ϵ=12라고 하자. |x−c|<δ이면 |f(x)−f(c)|<12를 만족하는 δ>0가 존재한다.
1). 무리수 a∈(c−δ,c+δ)∩I를 선택하는 경우
|f(a)−f(c)|=|1−f(c)|<12⇒−12<1−f(c)<12⇒−32<−f(c)<−12⇒12<f(c)<32
2). 유리수 a∈(c−δ,c+δ)∩Q를 선택하는 경우
|f(a)−f(c)|=|f(c)|<12⇒−12<f(c)<12
여기서, 두 함수값의 차이가 절대 작아질 수 없음을 증명하면 귀류법에 의해 모순이 되어 함수 f는 어떠한 지점에서도 연속이 아님이 증명된다.
|f(a)−f(b)|=|(f(a)−f(c))+(f(c)−f(b))|≤|f(a)−f(c)|+|f(b)−f(c)|=12+12=1
즉, 유리수와 무리수를 선택했을 때 두 함숫값의 차이가 좁혀지지 않으므로 함수 f는 어떠한 점에서도 연속이 아니다.
연습문제10. 방정식 ax3+2x2−1+bx3+x−2=0이 열린 구간 (−1,1) 사이에서 적어도 하나의 근이 있음을 증명하라. 이때, a와 b는 양수이다.
함수 ax3+2x2−1+bx3+x−2=0라고 하자.
f(x)=ax3+2x2−1+bx3+x−2=a(x+1)(x2+x−1)+b(x−1)(x2+x+2)=a(x−1)(x2+x+2)+b(x+1)(x2+x+1)(x+1)(x2+x−1)(x−1)(x2+x+2)
이때, f(x)=0이 되는 것은 f의 분자가 0이 되는 것과 동치이다. g(x)=a(x−1)(x2+x+2)+b(x+1)(x2+x+1)이라고 하면 g(−1)=−4a<0<6b=g(1)이고 함수 g는 연속함수이므로 정리4(IVT)에 의해 열린 구간 (−1,1)에서 g(c)=0↔f(c)=0을 만족하는 x=c가 적어도 하나 존재한다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.08.08 : 전체적인 스타일 수정
22.08.08 : 연습문제1-5 추가
22.08.09 : 연습문제6-10 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 미분 개요 (0) | 2021.10.22 |
|---|---|
| 미적분학 - 무한대 극한 (0) | 2021.09.07 |
| 미적분학 - 정확한 극한의 정의 (0) | 2021.08.25 |
| 미적분학 - 극한 법칙을 이용한 극한 계산하기 (0) | 2021.08.20 |
| 미적분학 - 함수의 극한 (0) | 2021.08.17 |
