안녕하세요. 지난 포스팅의 미적분학 - 역함수와 로그함수, 역삼각함수에서는 역함수의 정의와 함께 지수함수와 삼각함수의 역함수인 로그함수와 역삼각함수에 대해서 알아보았습니다. 특히, 역삼각함수를 정의하기 위해서는 삼각함수의 범위를 제한하여 일대일 대응 함수가 되야하는 것까지 언급하였습니다. 오늘은 미분을 향한 첫번째 발걸음으로 접선(tangent)에 대해서 간단하게 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
여러분, 혹시 접선을 의미하는 "tangent"라는 단어가 "touching"을 의미하는 라틴어에서 유래한다는 것을 아시나요? 이를 미루어볼 때 접선이라는 것은 어떤 것에 닿아있는 것을 의미한다고 볼 수 있습니다. 수학에서 말하는 접선은 곡선(curve)에 닿은 직선을 의미합니다. 단, 그냥 닿기만 해서는 안되겠죠? 이제부터는 이 정의에 대해서 좀 더 자세히 알아보겠습니다.
일단 간단하게 $y = x^{2}$ 함수의 점 $P(1, 1)$에서의 접선을 찾아보도록 하겠습니다. 접선은 기본적으로 직선입니다. 따라서 기울기 $m$과 $y$ 절편 $b$로 정의될 수 있습니다.
$$l : y = mx + b$$
그리고 정확히 1개의 직선을 표현하기 위해서는 2개의 점이 필요하기 때문에 $y = x^{2}$ 위의 임의의 점 $Q(x, x^{2})$을 하나 더 잡도록 하겠습니다. 단, $x = 1$인 점은 선택하지 않습니다. 그러면 직선 $PQ$의 기울기는 아래와 같습니다.
$$m_{PQ} = \frac{x^{2} - 1}{x - 1} = x + 1$$
예를 들어, $Q(1.5, 2.25)$라면 $m_{PQ} = 2.5$입니다. 하지만, 아직은 접선이라기보다는 직선입니다. 따라서 점 $Q$를 $P$에 더욱 가깝게 정해보도록 하겠습니다. $Q(1.1, 1.21)$이라면 $m_{PQ} = 2.1$이 되겠네요. 이를 수학적으로 표현하기 위해서 $\lim$라는 기호를 추가합니다.
$$\lim_{(x, x^{2}) \rightarrow (1, 1)} x + 1 = 2$$
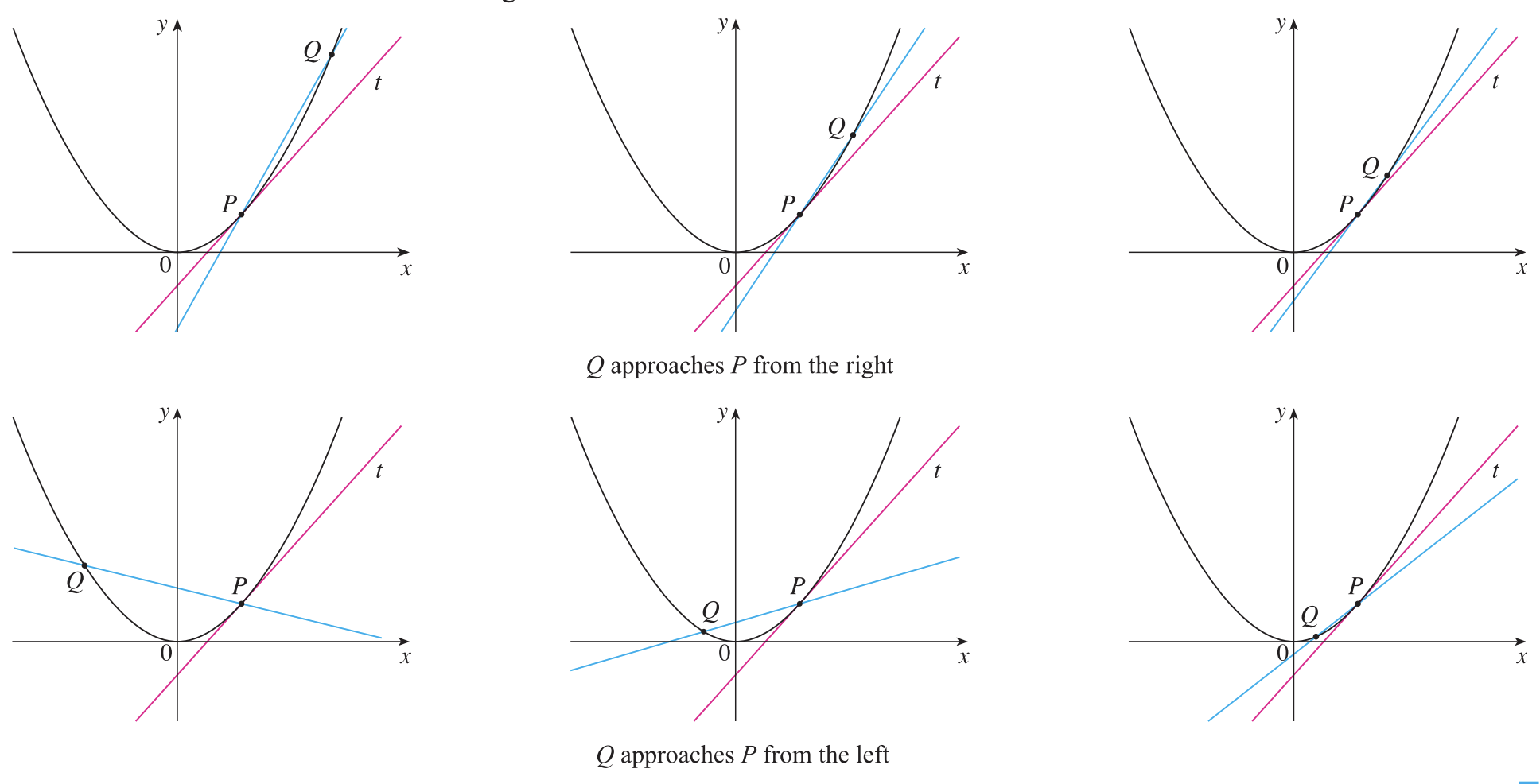
$(x, x^{2}) \rightarrow (1, 1)$로 근사되기 위해서는 $x \rightarrow 1$로 근사되는 방법밖에 없습니다. 위의 그림은 $x \rightarrow 1$에 다가갈 때 접선이 어떻게 변하는 지 보여주고 있습니다. 따라서 $y = x^{2}$의 점 P(1, 1)$에서의 접선의 기울기는 2임을 알 수 있습니다.
$$l : y - 1 = 2(x - 1) \rightarrow y = 2x - 1$$
연습문제1. 최대 1000갤런의 물을 담을 수 있는 물탱크가 있다고 하자. 이때, 물탱크는 30분만에 모든 물이 빠지는 구멍이 아래에 생겼다. 아래의 그래프는 30분동안 5분 간격으로 남은 물탱크 안의 물을 갤런으로 표시한 것이다.
| $t$(min) | 5 | 10 | 15 | 20 | 25 | 30 |
| $V$(gal) | 694 | 444 | 250 | 111 | 28 | 0 |
여기서, 점 $P(15, 250)$이라고 할 때 각 시간 $t = 5, 10, 20, 25, 30$과의 기울기를 구하여라.
1). $t = 5 \rightarrow m = \frac{694 - 250}{5 -15} = -\frac{444}{10}
2). $t = 10 \rightarrow m = \frac{444 - 250}{10 -15} = -\frac{194}{5}$
3). $t = 20 \rightarrow m = \frac{111 - 250}{20 -15} = -\frac{139}{5}$
4). $t = 25 \rightarrow m = \frac{28 - 250}{25 -15} = -\frac{222}{10}$
5). $t = 30 \rightarrow m = \frac{0 - 250}{30 -15} = -\frac{250}{15}$
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.06.06 : 연습문제1 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 극한 법칙을 이용한 극한 계산하기 (0) | 2021.08.20 |
|---|---|
| 미적분학 - 함수의 극한 (0) | 2021.08.17 |
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
| 미적분학 - 지수함수 (0) | 2021.08.14 |
| 미적분학 - 새로운 함수 만들기 (0) | 2021.08.11 |
