안녕하세요. 지난 포스팅의 미적분학 - 새로운 함수 만들기에서는 기존의 함수를 기반으로 새로운 함수를 만드는 방법에 대해서 알아보았습니다. 오늘은 지수 함수(Exponential Function)에 대해서 좀 더 자세하게 알아보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
지난 번에도 보셨다싶이 지수 함수는 기본적으로 $a \in \mathbb{R}_{+}$일 때 $f(x) = a^{x}$의 꼴을 지닌 함수를 의미합니다. 만약 $x = n \in \mathbb{Z}_{+}$라고 가정해보겠습니다. 그러면 $a^{n}$은 $a$를 $n$번 곱한 것과 동일한 결과를 얻습니다. 그리고 $x = 0$이면 $a$의 값에 관계없이 $f(0) = 1$입니다. 마지막으로 $x = \frac{p}{q}$의 유리수라면 $a^{\frac{p}{q}} = \sqrt[q]{x^{p}}$로 계산될 수 있습니다. 하지만, 한가지가 남았습니다.
$x$가 무리수(Irrational Number)라면 $f(x)$를 어떻게 정의할까?
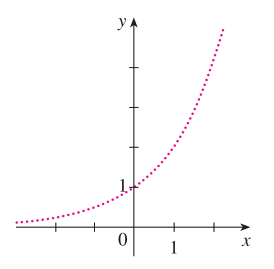
예를 들어 $2^{\pi}$나 $5^{\sqrt{2}}$가 있습니다. 일단 $x$가 유리수일때는 잘 정의되기 때문에 $x \in \mathbb{Q}$일 때 $f(x) = 2^{x}$의 그래프는 위와 같이 그릴 수 있습니다. 이제 저희의 목표는 저기 사이의 구멍을 메꾸면 됩니다. 그리고 저희는 $f(x)$가 증가 함수라는 것을 알고 있습니다. 따라서 저희는 증가 함수라는 조건을 이용해서 유리수로 채우지 못하는 영역을 근사시켜서 구하면 됩니다. 아주 간단하죠? 예시로 $2^{\pi}$를 찾아보도록 하겠습니다.
$$3 < \pi < 4 \Rightarrow 2^{3} = 8< 2^{\pi} < 16 = 2^{4} $$
아하~ 따라서 $2^{\pi}$는 8보다 크고 16보다 작은 값이라는 것을 알게 되었네요. 하지만, 이렇게 끝내면 아직 정확한 값을 찾지 못했기 때문에 한번 더 해보도록 하겠습니다. 참고로 왼쪽에서 오른쪽으로의 수식은 $f(x)$가 증가함수라는 조건을 이용한 것 입니다.
$$3.1 < \pi < 3.2 \Rightarrow 2^{3.1} = 8.57419 < 2^{\pi} < 9.18959 = 2^{3.2}$$
원래는 8~16 사이의 값이였지만 이번에는 8.57419 ~ 9.18959 사이의 값임을 알게 되었습니다. 하지만 한번 더 해보도록 하겠습니다.
$$3.14 < \pi < 3.15 \Rightarrow 2^{3.14} = 8.81524 < 2^{\pi} < 8.87656 = 2^{3.15}$$
이제 $2^{\pi} = 8.8xxx$라는 것을 알게 되었습니다. 만약, 더 정확한 값으로 근사하고 싶다면 이를 몇 번 더 반복하면 됩니다. 참고로 실제 $2^{\pi} = 8.8249778270762876238564296042080015817044108152714849266689598650...$입니다. 단순한 근사만으로도 소수점 첫번째 자리까지는 맞추었네요. 이와 같은 방법으로 모든 $f(x) = 2^{x}$의 비어있는 영역을 채울 수 있습니다.
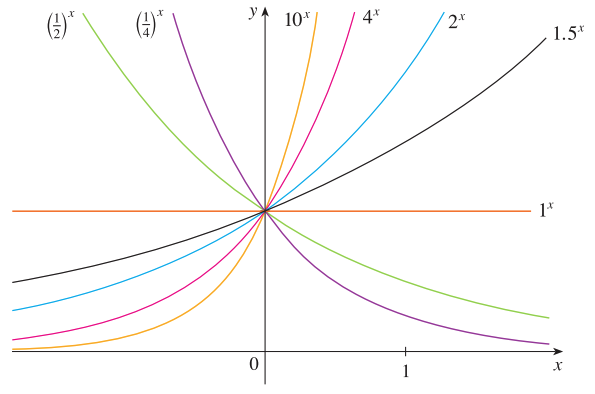
또한 지수 함수는 $a$의 범위에 따라서 형태가 달라집니다. 위의 그림을 보시면 될 거 같습니다. $a > 1$이면 증가 함수, $a = 1$이면 상수 함수, $0 < a < 1$이면 감소함수가 되는 것을 볼 수 있죠.
그리고 지수 함수에서 가장 중요한 연산 규칙 4가지가 있습니다. 이는 이후에 다양하게 사용되니 꼭 숙지하시길 바랍니다.
- $a^{x + y} = a^{x}a^{y}$
- $a^{x - y} = a^{x}/a^{y}$
- $(a^{x})^{y} = a^{xy}$
- $(ab)^{x} = a^{x}b^{x}$

마지막으로 자연상수 $e \approx 2.71828$ 입니다. 지수 함수를 설명할 때 빼놓을 수 없는 녀석이죠. 모든 과학 분야에서 항상 등장하는 마치 $\pi$같은 친구입니다. 자연상수를 밑으로 지수 함수 $f(x) = e^{x}$의 가장 큰 특징 중 하나는 $x = 0$에서의 기울기가 1이라는 점 입니다.
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 접선 (0) | 2021.08.16 |
|---|---|
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
| 미적분학 - 새로운 함수 만들기 (0) | 2021.08.11 |
| 미적분학 - 수학적 모델 (2) | 2021.08.10 |
| 미적분학 - 함수 (2) | 2021.08.09 |
