안녕하세요. 지난 포스팅의 미적분학 - 함수에서는 함수에 대한 정의와 함께 대칭함수인 짝함수와 기함수, 그리고 증가함수와 감소함수에 대해서 알아보았습니다. 오늘은 실제 세계의 문제를 풀기 위해서 방정식을 설계하는 모델링과 어떤 수학적 모델이 있는지에 대해서 알아보겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
1. 수학적 모델링(Mathematical Modeling)
정의1.수학적 모델(Mathematical Model)

수학적 모델은 실제 세계의 현상을 수학적으로 묘사(Mathematical Description)한 것이다.
설명
간단하게 예를 들면 자유낙하하는 공의 속도, 화학적 반응으로 만들어지는 부산물의 확산 등이 있습니다. 이러한 모델링은 함수나 방정식을 이용해서 이루어질 수 있습니다. 위 그림은 수학적 모델링의 단계를 설명하고 있습니다.
- 수학적 모델을 공식화 : 독립변수와 종속변수를 명확히 정하고 현상을 간단하게 만들기 위해서 몇 가지 가정을 추가한다.
- 알고있는 수학을 적용 : 수학적 모델로부터 어떤 결과를 얻어내기 위해서 미적분학, 미분방정식, 선형대수학 등의 방법론을 적용한다.
- 수학적 결론을 해석 : 얻은 결과를 해석하고 이를 실제 세계에 적용하여 어떤 의미인지 분석한다.
- 새로운 데이터에 대한 시험 : 1 ~ 3의 결과를 새로운 데이터에 적용하여 잘 들어맞는지(fit) 확인하고 수정한다.
예를 들어서 자유낙하하는 공의 속도를 모델링한다고 쳤을 때 독립변수는 시간, 종속변수는 속도로 정하게 됩니다. 그리고 문제를 간단하게 만들기 위해서 공과 공기 사이에 발생하는 마찰 등 다양한 외력을 무시합니다. 이를 시작으로 저희가 알고 있는 수학을 적용하고 결과를 해석한 뒤 실제로 공을 던졌을 때 동일한 결과가 나오는 지 검증합니다. 하지만 저희가 첫번째 단계에서한 가정으로 인해 오차가 발생할 것입니다. 이제다시 마찰 및 다른 외력을 하나씩 추가하면서 정확하게 모델링 될 수 있도록 작업을 반복합니다.
2. 수학적 모델(Mathematical Model)
수학적 모델링에서 중요한 것은 어떤 수학적 모델을 사용하느냐가 중요합니다. 이번에는 다양한 수학적 모델들에 대해서 알아보겠습니다.
1). 선형 함수(Linear Function) : $y = f(x) = mx + b$
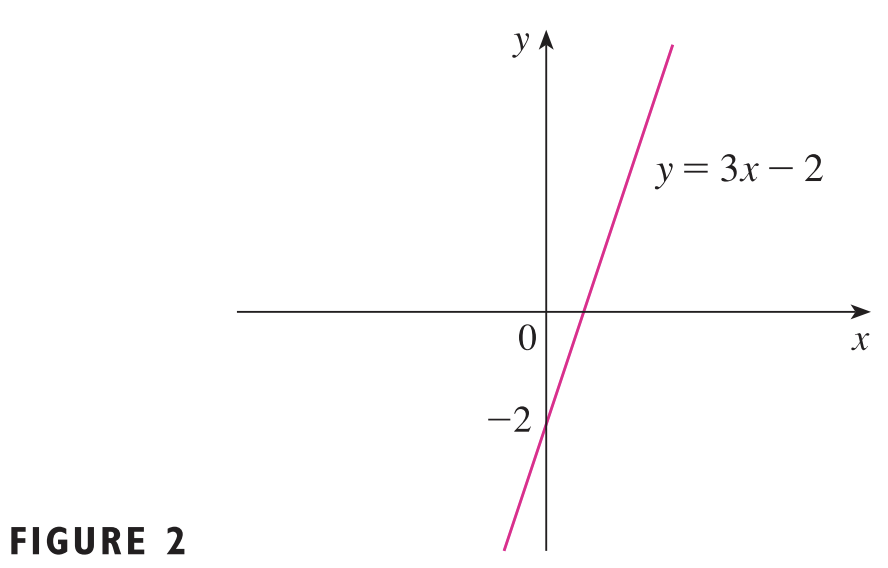
선형 모델은 위 그림과 같이 단순한 직선으로 수학적 모델들 중 가장 간단한 모델입니다. 크게 2개의 변수로 이루어져있습니다. $m$은 직선의 기울기, $b$는 $y$-절편을 의미합니다. 선형 모델의 가장 큰 특징은 모든 정의역에 대해서 일정한 비율로 커진다는 점 입니다.
2). 다항 함수(Polynomial Function) : $P(x) = a_{n}x^{n} + \cdots + a_{1}x + a_{0}$
다항 모델은 선형 모델보다 더 복잡한 모델로 $n + 1$개의 변수($a_{n}, \dots, a_{1}, a_{0}$)으로 이루어져 있는 수학적 모델입니다. 여기서 $a_{0}$는 선형 모델에서의 $b$와 동일한 역할로 $y$-절편을 의미합니다. 그리고 $a_{n}, \dots, a_{1}$은 계수(coefficient)라고 부릅니다. 다항식의 복잡도를 조절하는 파라미터가 바로 차수(degree) $n$입니다. $n$이 커지면 커질수록 다항 모델은 복잡한 데이터를 더 잘 표현할 수 있을 겁니다. 예를 들어 $P(x) = x^{6} - x^{5}$은 6차 다항식이 됩니다.
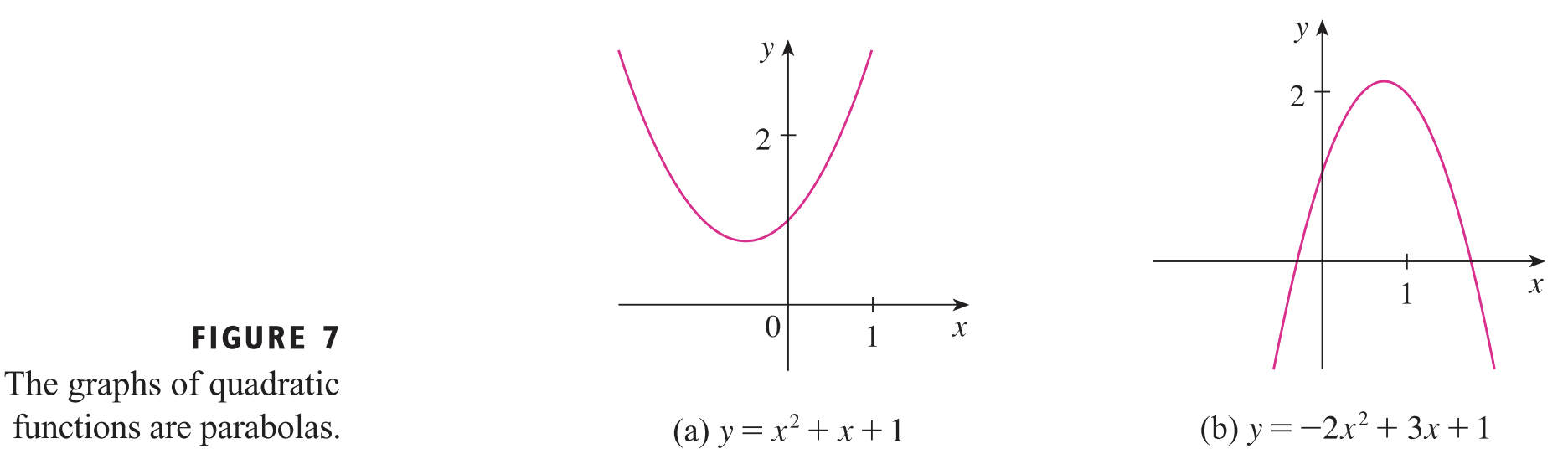
그리고 $n = 1$이라면 선형 모델이 되겠죠? 저희가 바로 아까 봤던 식과 동일해집니다. $n = 2$일 때는 이차 다항 모델(Quadratic Polynomial Model)이 됩니다. 이차 다항 모델에서는 $a_{2}$의 부호에 따라서 양수면 아래로 볼록한 (a) 그림, 음수면 위로 볼록한 (b) 그림이 됩니다.
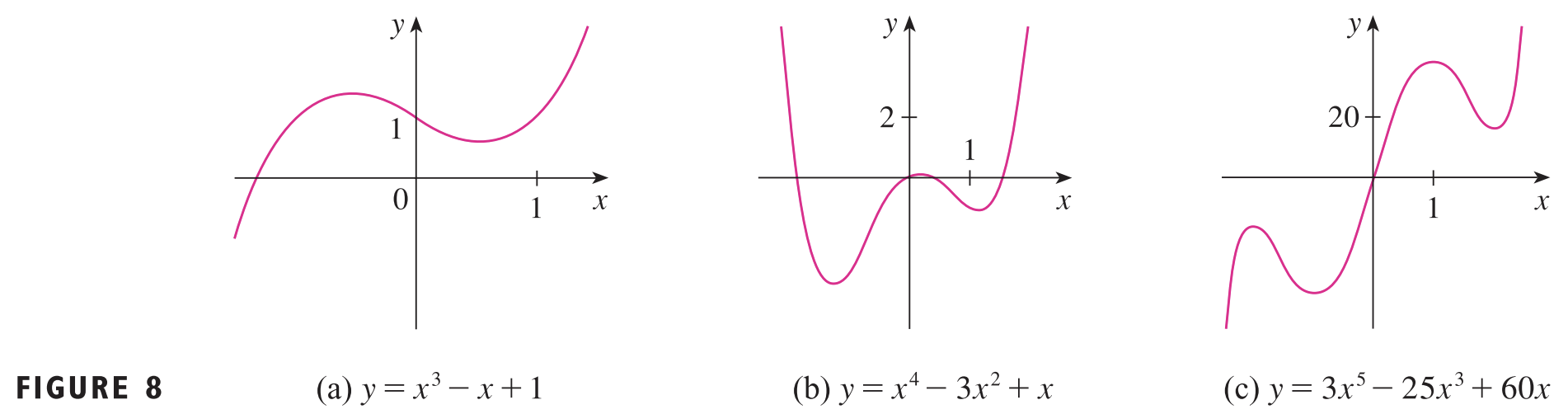
그렇다면 $n = 3$일 때는 어떨까요? 이 경우에는 삼차 다항 모델(Cubic Polynomial Model)이라고 부릅니다. 뿐만 아니라 위의 (b), (c) 처럼 4차, 5차 다항 모델도 만들어볼 수 있습니다.
3). 거듭제곱 함수(Power Function) : $f(x) = x^{a}$
거듭제곱 함수는 $a$에 따라서 그 모양이 결정됩니다.
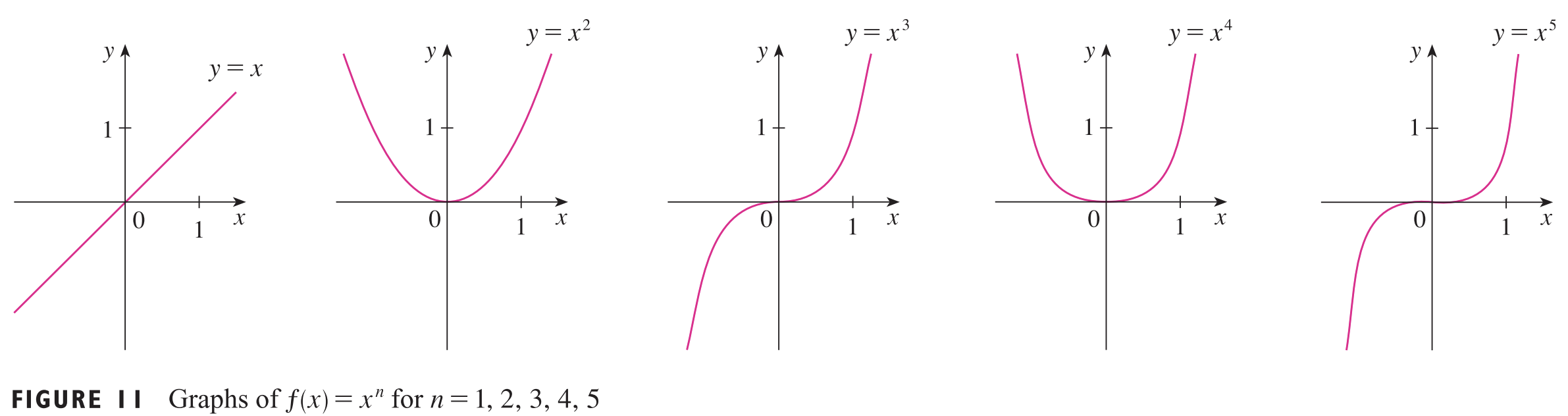
먼저, $a = n$이라면(여기서 $n$은 양의 정수입니다.) $f(x) = x^{n}$입니다. 즉, 저희가 다항 모델에서 다른 항 없이 최고차항만 있는 모델이 됩니다. 예를 들어 위 그림과 같이 $x^{1}, x^{2}, x^{3}, \dots$가 되겠네요.
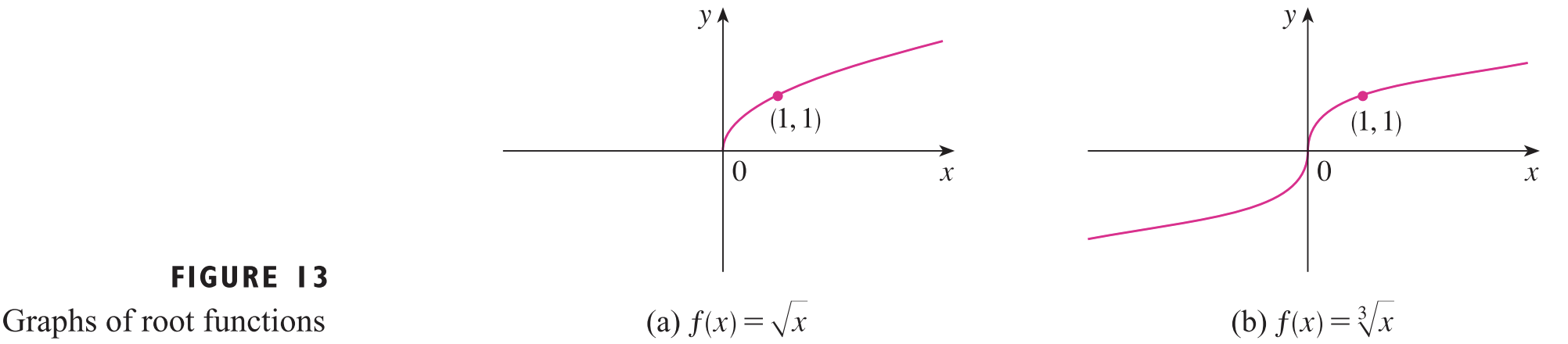
그리고 $a = \frac{1}{n}$이라면 $f(x) = x^{\frac{1}{n}} = \sqrt[n]{x}$입니다. 이러한 함수를 저희는 근 함수(root function)이라고 부르도록 하겠습니다. 만약, $n = 2$이라면 $f(x) = \sqrt{x}$가 되고 정의역은 $[0, \infty)$가 될 것 입니다(그림(a)). 그리고 $n = 3$이라면 $f(x) = \sqrt[3]{x}$가 되고 정의역은 $\mathbb{R}$이 될 것 입니다(그림(b)). $a = n$ 과 마찬가지로 $a = \frac{1}{n}$ 역시 $n$의 짝수, 홀수인지에 따라서 그 특정이 결정됩니다. $n$이 짝수면 그래프가 그림(a)와 유사하고 $n$이 홀수면 그래프가 그림(b)와 유사합니다.
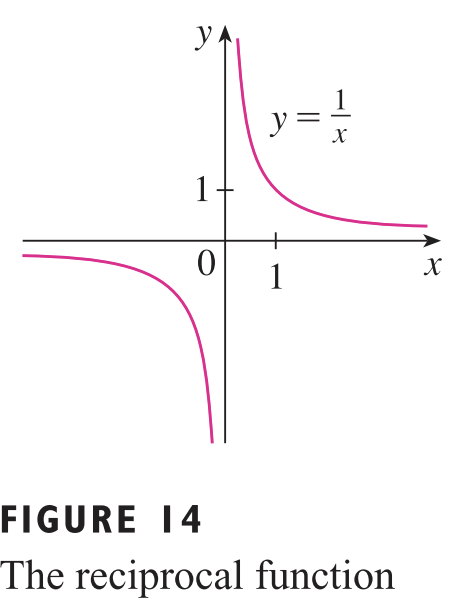
마지막으로 $a = 1$일 경우에는 $f(x) = \frac{1}{x}$가 됩니다. 이를 역함수(저희가 아는 $f^{-1}(x)$와는 다릅니다!! 모호성을 방지하기 위해서 해당 용어는 지양하도록 하겠습니다.) 또는 역수 함수라고 불립니다.
4).유리 함수(Rational Function) : $f(x) = \frac{P(x)}{Q(x)}$
유리 함수는 분자와 분모가 모두 다항 함수로 이루어진 함수입니다. 유리 함수에서 가장 중요한 점은 바로 정의역을 잘 봐야합니다. 왜냐하면 저희가 분수를 적을 때 가장 먼저 고려하는 것은 분모가 0이 되면 안되는 것이기 때문에 $Q(x) = 0$인 구간은 정의역에서 빼주어야하기 때문입니다.
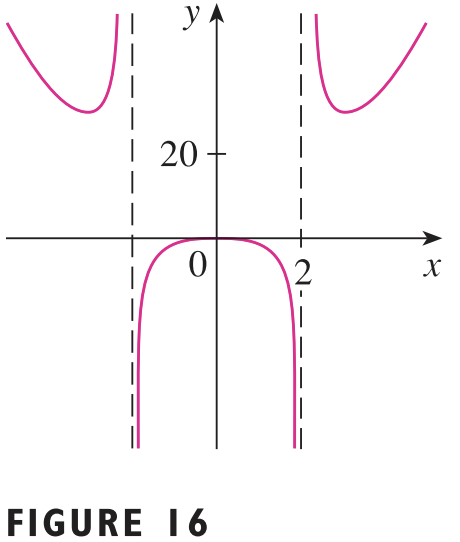
예를 들어서 $f(x) = \frac{2x^{4} - x^{2} + 1}{x^{2} - 4}$의 정의역은 $x^2 - 4 \neq 0$인 모든 구간이기 때문에 $\left(-\infty, -2\right) \cup \left(-2, 2\right) \cup \left(2, \infty\right)$입니다.
5). 대수 함수(Algebraic Function)
지금까지 보았던 선형 함수, 다항 함수, 거듭제곱 함수, 유리 함수는 아마 한번쯤은 들어보셧을 겁니다. 하지만, 대수 함수(Albebraic Function)에 대해서는 들어보진 못하진 분들이 많을 거 같습니다.
정의2.대수 함수(Algebraic Function)
함수 $f$가 대수적 연산(더하기, 빼기, 곱하기, 나누기, 제곱근)의 조합으로 이루어진다면 대수 함수이다.
설명
사실 위에 나온 대수 함수의 정의는 많은 수학 전공자 분들이 화가 나실만한 정의일 것 같습니다. 왜냐하면 더 정확한 정의가 따로 있기 때문입니다. 이 부분은 나중에 추가로 설명할 예정이니 지금은 이 정도로만 하고 넘어가도록 하겠습니다. 따라서 대수 함수의 예는 아래와 같습니다.
$$f(x) = \sqrt[5]{x^{10} + x^{6} - 1}$$
6). 삼각 함수(Trigometric Function)
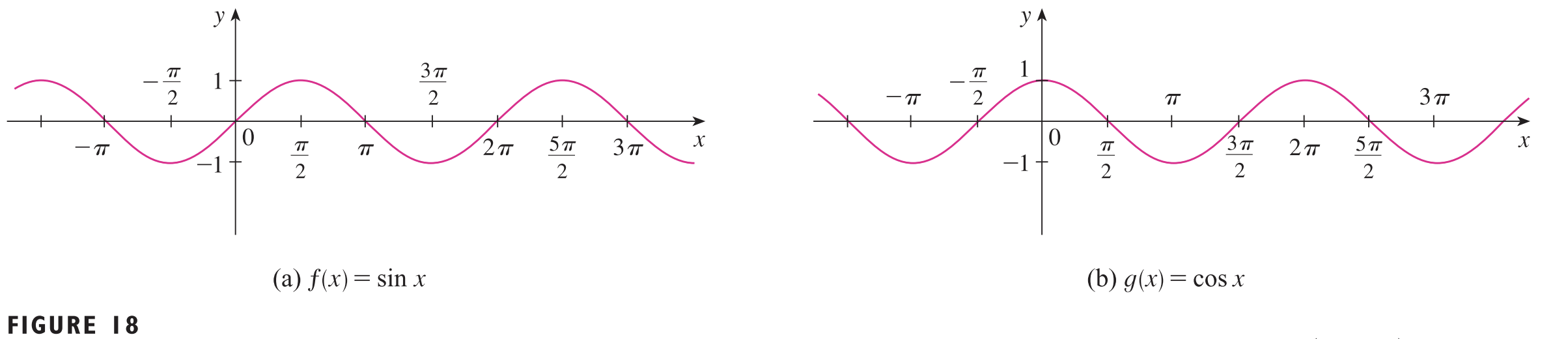
삼각 함수는 저희가 잘 알고있는 $\sin{x}$과 $\cos{x}$ 함수를 시작으로 만들어진 함수입니다. 따라서 $\tan{x} = \frac{\sin{x}}{\cos{x}}$ 역시 삼각함수가 되죠. 이러한 삼각 함수 중 가장 기초적인 $\sin{x}$와 $\cos{x}$은 항상 -1 ~ 1 사이의 값을 가지고 있습니다. 따라서 모든 $x$에 대해서 $|\sin{x}| \le 1, |\cos{x}| \le 1$을 만족하죠.
7). 지수 함수(Exponential Function) : $f(x) = a^{x}$
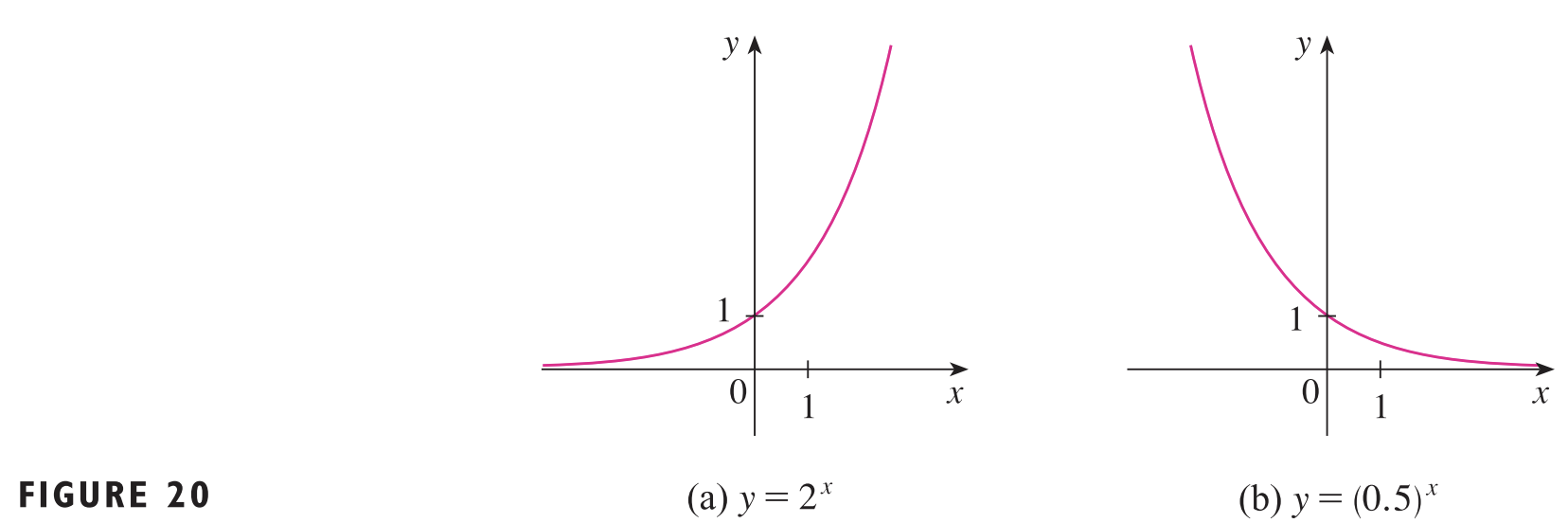
지수 함수는 $f(x) = a^{x}$ 꼴을 가진 함수입니다. 거듭제곱 함수 $f(x) = x^{a}$와 비교해보면 $a$와 $x$의 위치가 바뀐 것을 볼 수 있습니다. 그러므로 헷갈리시면 안됩니다. 거듭제곱 함수와 마찬가지로 $a$의 범위에 따라서 그 모양이 달라집니다. 만약 $a > 1$이라면 그림 (a)와 같이 우상향 그래프가 그려지고 $a < 1$이라면 그림 (b)와 같이 우하향 그래프가 그려집니다.
8). 로그 함수(Logarithmic Function) : $f(x) = \log_{a}{x}$
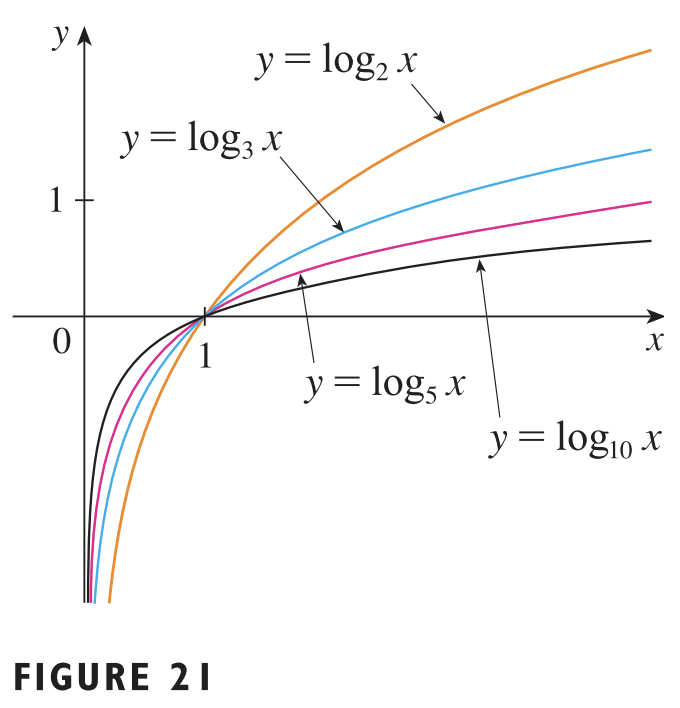
로그 함수는 지수 함수의 역함수(inverse function)입니다. 여기서 $a$는 밑(base)라고 불리며 $a$의 값에 따라서 그래프가 변화합니다. 로그 함수는 나중에 더 자세히 다루도록 하겠습니다.
9). 초월 함수(Transcendental Function)
초월 함수는 대수 함수가 아닌 모든 함수를 의미합니다.
연습문제1. $f(x) = \sqrt[5]{x}, g(x) = \sqrt{1 - x^{2}}, r(x) = \frac{x^{2} + 1}{x^{3} + x}, s(x) = \sin(x), t(x) = x + \frac{x^{2}}{\sqrt{x - 1}}$를 각각 멱함수, 무리함수, 다항함수, 유리함수, 대수함수, 삼각함수, 지수함수, 초월함수로 분류하라.
$f(x), g(x)$ : 무리함수
$r(x)$ : 유리함수
$s(x)$ : 삼각함수
$t(x)$ : 대수함수
연습문제2. $y = x^{2}, y = x^{5}, y = x^{8}$를 각각 아래의 그래프 중 어떤 함수에 적합한지 짝지어라.
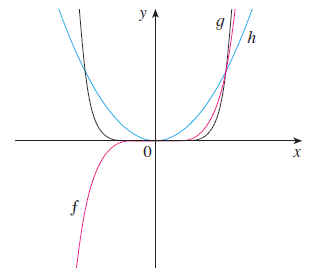
$h(x) = x^{2}, f(x) = x^{5}, g(x) = x^{8}$
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.06.10 : 연습문제1 - 2 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 접선 (0) | 2021.08.16 |
|---|---|
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
| 미적분학 - 지수함수 (0) | 2021.08.14 |
| 미적분학 - 새로운 함수 만들기 (0) | 2021.08.11 |
| 미적분학 - 함수 (2) | 2021.08.09 |
안녕하세요. 지난 포스팅의 미적분학 - 함수에서는 함수에 대한 정의와 함께 대칭함수인 짝함수와 기함수, 그리고 증가함수와 감소함수에 대해서 알아보았습니다. 오늘은 실제 세계의 문제를 풀기 위해서 방정식을 설계하는 모델링과 어떤 수학적 모델이 있는지에 대해서 알아보겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
1. 수학적 모델링(Mathematical Modeling)
정의1.수학적 모델(Mathematical Model)

수학적 모델은 실제 세계의 현상을 수학적으로 묘사(Mathematical Description)한 것이다.
설명
간단하게 예를 들면 자유낙하하는 공의 속도, 화학적 반응으로 만들어지는 부산물의 확산 등이 있습니다. 이러한 모델링은 함수나 방정식을 이용해서 이루어질 수 있습니다. 위 그림은 수학적 모델링의 단계를 설명하고 있습니다.
- 수학적 모델을 공식화 : 독립변수와 종속변수를 명확히 정하고 현상을 간단하게 만들기 위해서 몇 가지 가정을 추가한다.
- 알고있는 수학을 적용 : 수학적 모델로부터 어떤 결과를 얻어내기 위해서 미적분학, 미분방정식, 선형대수학 등의 방법론을 적용한다.
- 수학적 결론을 해석 : 얻은 결과를 해석하고 이를 실제 세계에 적용하여 어떤 의미인지 분석한다.
- 새로운 데이터에 대한 시험 : 1 ~ 3의 결과를 새로운 데이터에 적용하여 잘 들어맞는지(fit) 확인하고 수정한다.
예를 들어서 자유낙하하는 공의 속도를 모델링한다고 쳤을 때 독립변수는 시간, 종속변수는 속도로 정하게 됩니다. 그리고 문제를 간단하게 만들기 위해서 공과 공기 사이에 발생하는 마찰 등 다양한 외력을 무시합니다. 이를 시작으로 저희가 알고 있는 수학을 적용하고 결과를 해석한 뒤 실제로 공을 던졌을 때 동일한 결과가 나오는 지 검증합니다. 하지만 저희가 첫번째 단계에서한 가정으로 인해 오차가 발생할 것입니다. 이제다시 마찰 및 다른 외력을 하나씩 추가하면서 정확하게 모델링 될 수 있도록 작업을 반복합니다.
2. 수학적 모델(Mathematical Model)
수학적 모델링에서 중요한 것은 어떤 수학적 모델을 사용하느냐가 중요합니다. 이번에는 다양한 수학적 모델들에 대해서 알아보겠습니다.
1). 선형 함수(Linear Function) : $y = f(x) = mx + b$
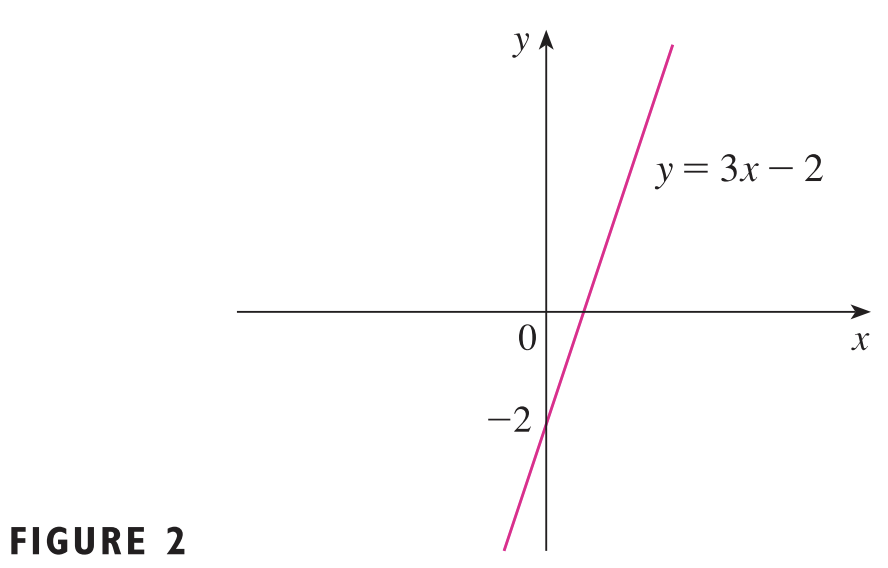
선형 모델은 위 그림과 같이 단순한 직선으로 수학적 모델들 중 가장 간단한 모델입니다. 크게 2개의 변수로 이루어져있습니다. $m$은 직선의 기울기, $b$는 $y$-절편을 의미합니다. 선형 모델의 가장 큰 특징은 모든 정의역에 대해서 일정한 비율로 커진다는 점 입니다.
2). 다항 함수(Polynomial Function) : $P(x) = a_{n}x^{n} + \cdots + a_{1}x + a_{0}$
다항 모델은 선형 모델보다 더 복잡한 모델로 $n + 1$개의 변수($a_{n}, \dots, a_{1}, a_{0}$)으로 이루어져 있는 수학적 모델입니다. 여기서 $a_{0}$는 선형 모델에서의 $b$와 동일한 역할로 $y$-절편을 의미합니다. 그리고 $a_{n}, \dots, a_{1}$은 계수(coefficient)라고 부릅니다. 다항식의 복잡도를 조절하는 파라미터가 바로 차수(degree) $n$입니다. $n$이 커지면 커질수록 다항 모델은 복잡한 데이터를 더 잘 표현할 수 있을 겁니다. 예를 들어 $P(x) = x^{6} - x^{5}$은 6차 다항식이 됩니다.

그리고 $n = 1$이라면 선형 모델이 되겠죠? 저희가 바로 아까 봤던 식과 동일해집니다. $n = 2$일 때는 이차 다항 모델(Quadratic Polynomial Model)이 됩니다. 이차 다항 모델에서는 $a_{2}$의 부호에 따라서 양수면 아래로 볼록한 (a) 그림, 음수면 위로 볼록한 (b) 그림이 됩니다.

그렇다면 $n = 3$일 때는 어떨까요? 이 경우에는 삼차 다항 모델(Cubic Polynomial Model)이라고 부릅니다. 뿐만 아니라 위의 (b), (c) 처럼 4차, 5차 다항 모델도 만들어볼 수 있습니다.
3). 거듭제곱 함수(Power Function) : $f(x) = x^{a}$
거듭제곱 함수는 $a$에 따라서 그 모양이 결정됩니다.

먼저, $a = n$이라면(여기서 $n$은 양의 정수입니다.) $f(x) = x^{n}$입니다. 즉, 저희가 다항 모델에서 다른 항 없이 최고차항만 있는 모델이 됩니다. 예를 들어 위 그림과 같이 $x^{1}, x^{2}, x^{3}, \dots$가 되겠네요.
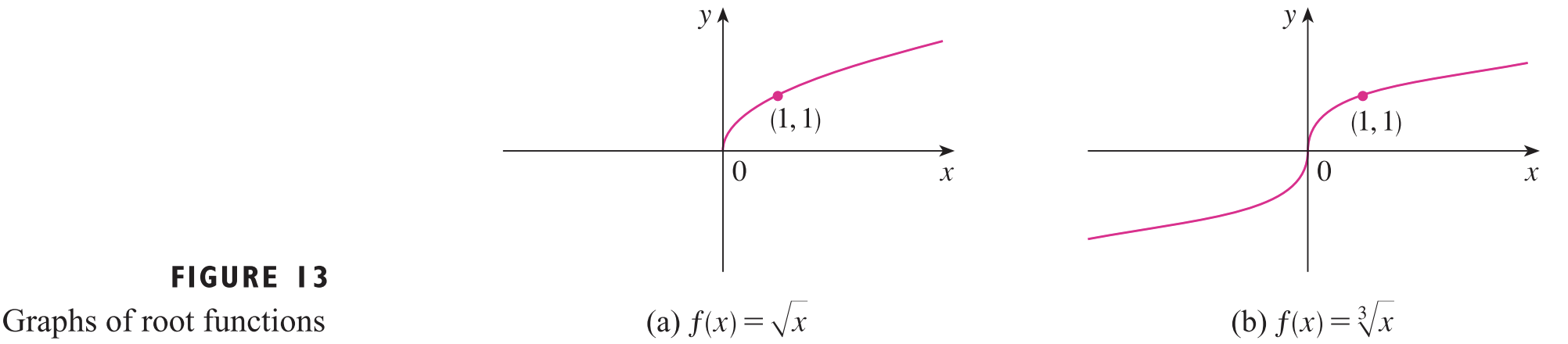
그리고 $a = \frac{1}{n}$이라면 $f(x) = x^{\frac{1}{n}} = \sqrt[n]{x}$입니다. 이러한 함수를 저희는 근 함수(root function)이라고 부르도록 하겠습니다. 만약, $n = 2$이라면 $f(x) = \sqrt{x}$가 되고 정의역은 $[0, \infty)$가 될 것 입니다(그림(a)). 그리고 $n = 3$이라면 $f(x) = \sqrt[3]{x}$가 되고 정의역은 $\mathbb{R}$이 될 것 입니다(그림(b)). $a = n$ 과 마찬가지로 $a = \frac{1}{n}$ 역시 $n$의 짝수, 홀수인지에 따라서 그 특정이 결정됩니다. $n$이 짝수면 그래프가 그림(a)와 유사하고 $n$이 홀수면 그래프가 그림(b)와 유사합니다.

마지막으로 $a = 1$일 경우에는 $f(x) = \frac{1}{x}$가 됩니다. 이를 역함수(저희가 아는 $f^{-1}(x)$와는 다릅니다!! 모호성을 방지하기 위해서 해당 용어는 지양하도록 하겠습니다.) 또는 역수 함수라고 불립니다.
4).유리 함수(Rational Function) : $f(x) = \frac{P(x)}{Q(x)}$
유리 함수는 분자와 분모가 모두 다항 함수로 이루어진 함수입니다. 유리 함수에서 가장 중요한 점은 바로 정의역을 잘 봐야합니다. 왜냐하면 저희가 분수를 적을 때 가장 먼저 고려하는 것은 분모가 0이 되면 안되는 것이기 때문에 $Q(x) = 0$인 구간은 정의역에서 빼주어야하기 때문입니다.

예를 들어서 $f(x) = \frac{2x^{4} - x^{2} + 1}{x^{2} - 4}$의 정의역은 $x^2 - 4 \neq 0$인 모든 구간이기 때문에 $\left(-\infty, -2\right) \cup \left(-2, 2\right) \cup \left(2, \infty\right)$입니다.
5). 대수 함수(Algebraic Function)
지금까지 보았던 선형 함수, 다항 함수, 거듭제곱 함수, 유리 함수는 아마 한번쯤은 들어보셧을 겁니다. 하지만, 대수 함수(Albebraic Function)에 대해서는 들어보진 못하진 분들이 많을 거 같습니다.
정의2.대수 함수(Algebraic Function)
함수 $f$가 대수적 연산(더하기, 빼기, 곱하기, 나누기, 제곱근)의 조합으로 이루어진다면 대수 함수이다.
설명
사실 위에 나온 대수 함수의 정의는 많은 수학 전공자 분들이 화가 나실만한 정의일 것 같습니다. 왜냐하면 더 정확한 정의가 따로 있기 때문입니다. 이 부분은 나중에 추가로 설명할 예정이니 지금은 이 정도로만 하고 넘어가도록 하겠습니다. 따라서 대수 함수의 예는 아래와 같습니다.
$$f(x) = \sqrt[5]{x^{10} + x^{6} - 1}$$
6). 삼각 함수(Trigometric Function)

삼각 함수는 저희가 잘 알고있는 $\sin{x}$과 $\cos{x}$ 함수를 시작으로 만들어진 함수입니다. 따라서 $\tan{x} = \frac{\sin{x}}{\cos{x}}$ 역시 삼각함수가 되죠. 이러한 삼각 함수 중 가장 기초적인 $\sin{x}$와 $\cos{x}$은 항상 -1 ~ 1 사이의 값을 가지고 있습니다. 따라서 모든 $x$에 대해서 $|\sin{x}| \le 1, |\cos{x}| \le 1$을 만족하죠.
7). 지수 함수(Exponential Function) : $f(x) = a^{x}$

지수 함수는 $f(x) = a^{x}$ 꼴을 가진 함수입니다. 거듭제곱 함수 $f(x) = x^{a}$와 비교해보면 $a$와 $x$의 위치가 바뀐 것을 볼 수 있습니다. 그러므로 헷갈리시면 안됩니다. 거듭제곱 함수와 마찬가지로 $a$의 범위에 따라서 그 모양이 달라집니다. 만약 $a > 1$이라면 그림 (a)와 같이 우상향 그래프가 그려지고 $a < 1$이라면 그림 (b)와 같이 우하향 그래프가 그려집니다.
8). 로그 함수(Logarithmic Function) : $f(x) = \log_{a}{x}$

로그 함수는 지수 함수의 역함수(inverse function)입니다. 여기서 $a$는 밑(base)라고 불리며 $a$의 값에 따라서 그래프가 변화합니다. 로그 함수는 나중에 더 자세히 다루도록 하겠습니다.
9). 초월 함수(Transcendental Function)
초월 함수는 대수 함수가 아닌 모든 함수를 의미합니다.
연습문제1. $f(x) = \sqrt[5]{x}, g(x) = \sqrt{1 - x^{2}}, r(x) = \frac{x^{2} + 1}{x^{3} + x}, s(x) = \sin(x), t(x) = x + \frac{x^{2}}{\sqrt{x - 1}}$를 각각 멱함수, 무리함수, 다항함수, 유리함수, 대수함수, 삼각함수, 지수함수, 초월함수로 분류하라.
$f(x), g(x)$ : 무리함수
$r(x)$ : 유리함수
$s(x)$ : 삼각함수
$t(x)$ : 대수함수
연습문제2. $y = x^{2}, y = x^{5}, y = x^{8}$를 각각 아래의 그래프 중 어떤 함수에 적합한지 짝지어라.

$h(x) = x^{2}, f(x) = x^{5}, g(x) = x^{8}$
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.06.10 : 연습문제1 - 2 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 접선 (0) | 2021.08.16 |
|---|---|
| 미적분학 - 역함수와 로그함수, 역삼각함수 (1) | 2021.08.15 |
| 미적분학 - 지수함수 (0) | 2021.08.14 |
| 미적분학 - 새로운 함수 만들기 (0) | 2021.08.11 |
| 미적분학 - 함수 (2) | 2021.08.09 |
