안녕하세요. 지난 포스팅의 미적분학 - 선적분에서는 기존에 저희가 보았던 축이나 평면을 기준으로하는 적분이 아닌 매개변수 곡선 상에서의 적분인 선적분에 대해서 알아보았습니다. 오늘은 보다 이론적인 내용으로 선적분을 미적분학 기본정리와 연결지어보도록 하겠습니다.
일단, 선적분을 다시 복습해보면 함수 $f(x, y)$의 변수들이 각각 매개변수 $a \le t \le b$에 대한 함수 $x = x(t)$와 $y = y(t)$로 정의된다고 가정할 때 곡선 $C$에서 아래와 같이 적분할 수 있습니다.
$$\int_{C} f(x, y) \; ds = \int_{a}^{b} f(x(t), y(t)) \sqrt{\left(\frac{dx}{dt}\right)^{2} + \left(\frac{dy}{dt}\right)^{2}} \; dt$$
그리고 미적분학 - 미적분학 기본정리의 내용도 복습해보도록 하겠습니다. 미적분학 기본정리는 쉽게 설명하면 미분과 적분 사이의 관계를 설명하는 정리입니다. 두 개의 정리로 이루어져 있으면 특히 오늘은 두번째 정리에 대해서 집중해보도록 하겠습니다. 함수 $F(x)$를 $f(x)$의 적분함수라고 하겠습니다.
$$\int_{a}^{b} f(x) \; dx = F(b) - F(a)$$
이때, 피적분함수 $f(x)$는 닫힌 구간 $[a, b]$에서 연속함수입니다. 위 정리에 따르면 $f(x) = F^{'}(x)$이기 때문에 아래와 같이 쓸 수 있겠죠.
$$\int_{a}^{b} F^{'}(x) \; dx = F(b) - F(a)$$
즉, 미분된 함수를 구간 $[a, b]$에서 적분한다는 것은 기존 함수 $F(x)$의 윗끝 값에서 아랫끝 값을 빼주면 되는 것입니다. 이를 다변수 함수로 어떻게 확장할 수 있을까요? 미적분학 - 기울기벡터에서는 다변수 함수에서의 미분인 기울기벡터를 계산하는 방법을 알려주고 있습니다. 따라서, 저희는 단변수 함수에 대한 미적분학 기본정리를 다변수 함수로 확장할 때 기울기벡터를 사용하면 된다는 것을 알 수 있죠.
정리1.
곡선 $C$를 $a \le t \le b$에서 벡터함수 $\mathbf{r}(t)$의 부드러운 곡선이라고 하자. 그리고 함수 $f$를 미분가능한 다변수 함수로 기울기벡터 $\nabla f$가 곡선 $C$에서 연속인 함수라고 할 때, 다변수 함수의 곡선 $C$에서의 선적분에 대한 미적분학 기본정리는 아래와 같다.
$$\int_{C} \nabla f \cdot d\mathbf{r} = f(\mathbf{r}(b)) - f(\mathbf{r}(a))$$
증명
$$\begin{align*} \int_{C} \nabla f \cdot d \mathbf{r} &= \int_{a}^{b} \nabla f(\mathbf{r}(a)) \cdot \mathbf{r}^{'}(t) \; dt \\ &= \int_{a}^{b} \left(\frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt} + \frac{\partial f}{\partial z} \frac{dz}{dt}\right) \; dt \\ &= \int_{a}^{b} \frac{d}{dt} f(\mathbf{r}(t)) \; dt \\ &= f(\mahtbf{r}(a)) - f(\mathbf{r}(b))\end{align*}$$
설명
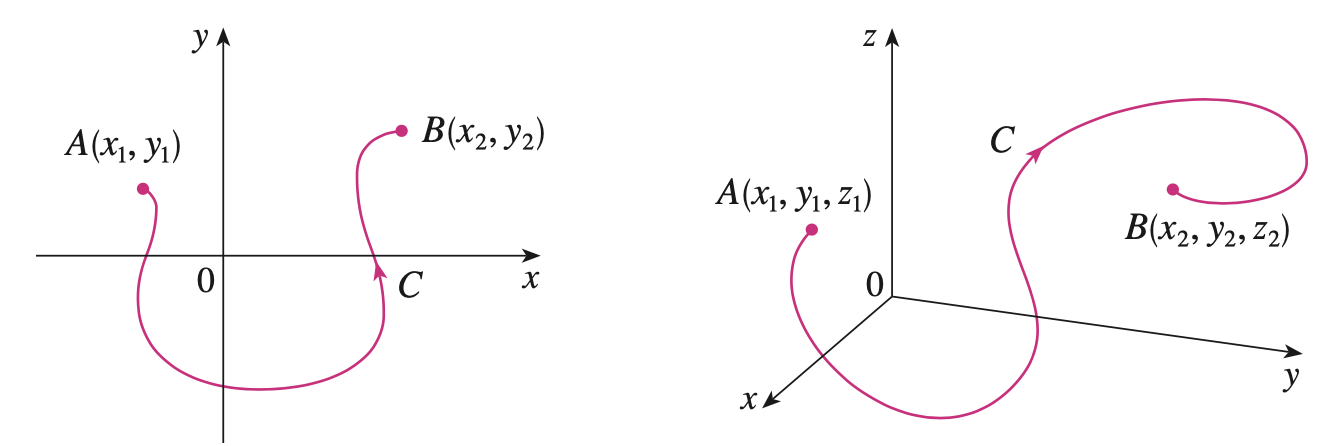
위 정리는 곡선 $C$에서 다변수 함수의 기울기벡터에 대한 선적분을 수행할 때 오직 시점 $A$와 종점 $B$만 신경쓰면 된다는 것을 알려주고 있습니다. 예를 들어, 이차원 곡선 $C$에서는 아래와 같은 결과를 얻을 수 있습니다.
$$\int_{C} \nabla f \cdot d\mathbf{r} = f(\mathbf{r}(b)) - f(\mathbf{r}(a)) = f(x_{1}, y_{1}) - f(x_{2}, y_{2})$$
그리고 삼차원 곡선에는 아래와 같은 결과를 얻을 수 있죠.
$$\int_{C} \nabla f \cdot d\mathbf{r} = f(\mathbf{r}(b)) - f(\mathbf{r}(a)) = f(x_{1}, y_{1}, z_{1}) - f(x_{2}, y_{2}, z_{2})$$
위와 같이 어떠한 곡선의 경로에 관계없이 단순히 곡선의 시점과 종점에만 의존하는 선적분을 경로의 독립성(independence of path)라고 합니다. 또한, 이를 포함하는 벡터장인 $D$를 보존장(conservative vector field)라고 합니다. 다음으로 저희가 고려해볼것은 임의의 벡터함수 $\mathbf{F}$에 대해서도 경로의 독립성이 성립할 수 있을지에 대한 의문입니다.
정리2.
정의역 $D$에서 정의된 벡터함수 $\mathbf{F}$가 있다고 하자. 정의역 $D$에서 $\int_{C} \mathbf{F} \cdot d\mathbf{r}$이 경로에 대해 독립적인 것은 정의역 $D$ 내의 임의의 폐곡선(closed curve) $C$에 대해서 $\int_{C} \mathbf{F} \cdot d\mathbf{r} = 0$과 동치이다.
설명

정리2을 이해하기 위해서는 폐곡선(closed curve)에 대한 개념부터 이해해야합니다. 폐곡선이란 곡선 중 시점과 종점이 동일한 곡선으로 $\mathbf{r}(a) = \mathbf{r}(b)$인 곡선을 의미합니다.
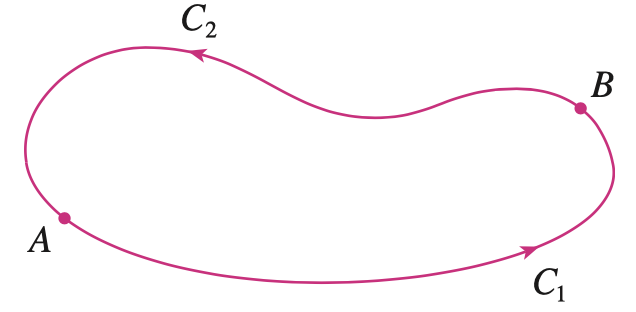
먼저, 정리2을 증명하기 위해 정의역 $D$에서 정의된 벡터함수 $\mathbf{F}$가 있다고 가정하겠습니다. 그리고 임의의 폐곡선 $C$가 정의역 $D$에서 정의되었다고 가정하죠. 저희는 폐곡선 $C$에서 임의의 2개 점 $A$와 $B$를 선택하도록 하겠습니다. 그러면 위와 같이 점 $A$와 $B$가 찍히겠죠. 여기서 저희는 점 $A$에서 $B$로의 곡선을 $C_{1}$이라고 하고, 점 $B$에서 $A$로의 곡선을 $C_{2}$라고 하겠습니다.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} + \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} - \int_{-C_{2}} \cdot d\mathbf{r} \\ &= 0\end{align*}$$
여기서 저희는 미적분학 - 선적분에서 곡선 $C$를 부드러운 곡선 $C_{1}$와 $C_{2}$로 쪼갰을 때 각 곡선에 대한 선적분의 결과를 합한다는 결과를 먼저 적용하였습니다. 그리고 $-C_{2}$를 $C_{2}$의 방향을 반대로 바뀐 곡선이라고 정의했을 때 $C_{1}$과 $-C_{2}$는 동일한 시점과 종점을 공유하게 됩니다. 이때, $\int_{C} \mathbf{F} \cdot d\mathbf{r}$이 경로에 대해서 독립적이라고 하였기 때문에 $\int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} = \int_{-C_{2}} \mathbf{F} \cdot d\mathbf{r}$이 성립합니다. 따라서, $\int_{C} \mathbf{F} \cdot d\mathbf{r} = 0$이 되는 것이죠.
이번에는 반대로 증명해보겠습니다. 일단, 벡터함수 $\mathbf{F}$가 정의된 정의역 $D$의 임의의 곡선 $C$에 대해서 $\int_{C} \mathbf{F} \cdot d\mathbf{r} = 0$이라고 하겠습니다. 저희는 임의의 점 $A$와 $B$를 선택한 뒤 두 점 사이의 임의의 2개의 경로 $C_{1}$과 $C_{2}$가 존재한다고 가정하겠습니다. 그리고 곡선 $C$는 두 곡선 $C_{1}$과 $-C_{2}$가 이어진 것으로 고려한다고 하죠.
$$\begin{align*} 0 &= \int_{C} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} + \int_{-C_{2}} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} - \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \\ \Rightarrow& \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} = \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \end{align*}$$
위 수식의 마지막 결론은 시점과 종점이 동일한 임의의 두 곡선 $C_{1}$와 $C_{2}$에 대한 선적분을 수행할 때 동일한 결과를 준다는 것입니다. 따라서, 경로에 대해서 무관하다는 뜻이 되겠네요.
정리3.
벡터함수 $\mathbf{F}$를 연결된(connected) 열린(open) 영역 $D$에서 연속인 벡터장이라고 가정하자. 만약, $\int_{C} \mathbf{F} \cdot d\mathbf{r}$이 영역 $D$에서 경로에 무관하다고 할 때 $\mathbf{F}$는 영역 $D$에서 보존장이며 이는 $\nabla f = \mathbf{F}$를 만족하는 함수 $f$가 존재함을 의미한다.
설명
정리3을 증명하기 위해 영역 $D$에서 고정점(fixed point) $A(a, b)$를 선택하겠습니다. 그리고 저희의 목표는 $\nabla f = \mathbf{F}$를 만족하는 함수 $f$가 존재함을 보여야하기 때문에 저희가 원하는 퍼텐셜 함수 $f$를 영역 $D$에서 임의의 점 $(x, y)$에 대해서 아래와 같이 정의하도록 하겠습니다.
$$f(x, y) = \int_{(a, b)}^{(x, y)} \mathbf{F} \cdot d\mathbf{r}$$
이때, 정리3의 조건에 의해 $\int_{C} \mathbf{F} \cdot d\mathbf{r}$이 영역 $D$에서 경로에 무관하기 때문에 $f(x, y)$를 얻기 위해 점 $(a, b)$에서 $(x, y)$의 어떠한 경로 $C$를 선택해도 상관없습니다.
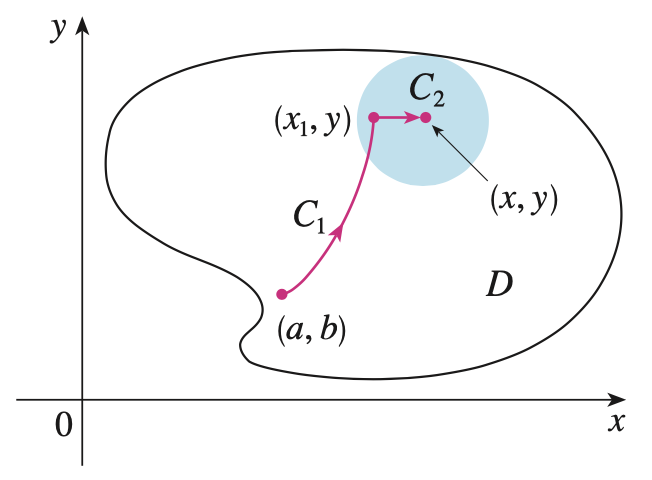
또한 영역 $D$가 연결된 열린 영역이라는 조건을 가지고 있기 때문에 위 그림과 같이 점 $(x, y)$를 중심으로 하고 영역 $D$에 포함되는 열린 디스크를 잡을 수 있습니다. 저희는 열린 디스크의 내부에서 $x_{1} < x$를 만족하는 임의의 점 $(x_{1}, y)$를 선택하도록 하겠습니다. 그리고 곡선 $C_{1}$을 점 $(a, b)$에서 점 $(x_{1}, y)$로의 경로, $C_{2}$를 점 $(x_{1}, y)$에서 $(x, y)$로의 경로라고 정의하고 곡선 $C$는 두 곡선 $C_{1}$과 $C_{2}$의 합집합이라고 정의하겠습니다. 따라서, 저희는 퍼텐셜 함수 $f(x, y)$를 아래와 같이 계산할 수 있죠.
$$\begin{align*} f(x, y) &= \int_{(a, b)}^{(x, y)} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} + \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{(a, b)}^{(x_{1}, y)} \mathbf{F} \cdot d\mathbf{r} + \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \end{align*}$$
이때, 위 식에서 첫번째 적분은 $x$에 무관하기 때문에 $x$에 대해서 편미분하면 0이 됩니다.
$$\frac{\partial f}{\partial x} = 0 + \frac{\partial }{\partial x} \int_{C_{2}} \mathbf{F} \cdot \mathbf{r}$$
또한, $\mathbf{F}$가 벡터함수이기 때문에 $P(x, y)$와 $Q(x, y)$에 대해서 $\mathbf{F} = P\mathbf{i} + Q\mathbf{j}$이기 때문에 $\int_{C_{2}} \mathbf{F} \cdot \mathbf{r} = \int_{C_{2}} P \; dx + Q \; dy$가 됩니다. 여기서, 주의해야할 점은 $C_{2}$ 상에서 $y$는 변하지 않는 상수입니다. 따라서, $dy = 0$이죠. 이제, $x_{1} \le t \le x$를 만족하는 매개변수 $t$를 정의하게 되면 미적분학 기본정리를 적용해서 저희는 아래의 식을 얻을 수 있습니다.
$$\begin{align*} \frac{\partial f}{\partial x} &= 0 + \frac{\partial }{\partial x} \int_{C_{2}} \mathbf{F} \cdot \mathbf{r} \\ &= \frac{\partial }{\partial x}\int_{C_{2}} P \; dx + Q \; dy \\ &= \frac{\partial }{\partial x} \int_{x_{1}}^{x} P(t, y) \; dt \\ &= P(x, y) \end{align*}$$
이와 동일한 방식으로 $y_{1} < y$를 만족하는 임의의 점 $(x, y_{1})$를 선택한 뒤 진행하면 $y$에 대한 $f(x, y)$의 편미분 결과도 얻을 수 있습니다.
$$\begin{align*} \frac{\partial f}{\partial y} &= \frac{\partial }{\partial y}\int_{C_{2}} P \; dx + Q \; dy \\ &= \frac{\partial }{\partial y} \int_{y_{1}}^{y} Q(x, t) \; dt \\ &= Q(x, y) \end{align*}$$
따라서, 저희는 아래와 같은 결과를 얻을 수 있습니다.
$$\mathbf{F} = P\mathbf{i} + Q\mathbf{j} = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} = \nabla f$$
이는 곧 벡터장 $\mathbf{F}$가 보존장임을 의미하기 때문에 정리3은 증명됩니다.
정리4.
벡터함수 $\mathbf{F}(x, y) = P(x, y) \mathbf{i} + Q(x, y) \mathbf{j}$가 보존장이고 $P$와 $Q$가 정의역 $D$에서 연속 편도함수를 가진다고 할 때 $\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$가 성립한다.
설명

정리4는 영역 $D$가 특별한 타입일 때만 성립하는 정리입니다. 이를 설명하기 위해 단순 곡선(simple curve)에 대한 개념을 이해해야합니다. 단순 곡선이란 쉽게 말해 전혀 꼬여있지 않은 곡선을 의미합니다. 위 그림에서는 아래의 왼쪽 그림이 되겠네요.
정리5.
열린 단순 연결 영역 $D$에서 정의된 벡터함수 $\mathbf{F}(x, y) = P(x, y) \mathbf{i} + Q(x, y) \mathbf{j}$가 있다고 가정하자. 영역 $D$에서 함수 $P$와 $Q$가 연속인 편도함수를 가지고 $\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$가 성립한다고 할 때 벡터장 $\mathbf{F}$는 보존장이다.
설명
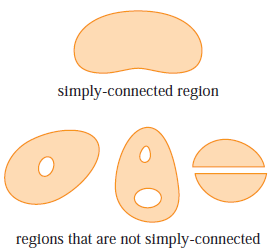
정리5를 이해하기 위해 더 강력한 조건을 가진 영역 $D$의 모양을 이해할 필요가 있습니다. 단순 연결 영역이라는 것은 위의 그림과 같이 중간이 구멍이 없으며 끊어지지 않은 영역을 의미합니다. 위 영역에서 정의된 벡터장 $\mathbf{F}$가 보존장일 조건에 대해서 설명하는 정리이죠. 위 정리는 앞으로 저희가 배울 가장 중요한 정리인 그린 정리(Green's Theorem)의 기초가 되기 때문에 알아두시는 것이 중요합니다.
예제1. 벡터장 $\mathbf{F}(x, y) = (x - y) \mathbf{i} + (x - 2) \mathbf{j}$가 보존장인지 아닌지 결정하라.
$P(x, y) = x - y$ 그리고 $Q(x, y) = x - 2$라고 하자. 그러면 $\frac{\partial P}{\partial y} = -1$이고 $\frac{\partial Q}{\partial x} = 1$이기 때문에 두 편도함수가 갔지 않으므로 벡터장 $\mathbf{F}$는 보존장이 아니다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 회전과 발산 (0) | 2022.07.26 |
|---|---|
| 미적분학 - 그린 정리 (0) | 2022.07.25 |
| 미적분학 - 선적분 (0) | 2022.07.15 |
| 미적분학 - 벡터장 (0) | 2022.07.13 |
| 미적분학 - 다중적분의 변수변환법 (0) | 2022.07.11 |
안녕하세요. 지난 포스팅의 미적분학 - 선적분에서는 기존에 저희가 보았던 축이나 평면을 기준으로하는 적분이 아닌 매개변수 곡선 상에서의 적분인 선적분에 대해서 알아보았습니다. 오늘은 보다 이론적인 내용으로 선적분을 미적분학 기본정리와 연결지어보도록 하겠습니다.
일단, 선적분을 다시 복습해보면 함수 $f(x, y)$의 변수들이 각각 매개변수 $a \le t \le b$에 대한 함수 $x = x(t)$와 $y = y(t)$로 정의된다고 가정할 때 곡선 $C$에서 아래와 같이 적분할 수 있습니다.
$$\int_{C} f(x, y) \; ds = \int_{a}^{b} f(x(t), y(t)) \sqrt{\left(\frac{dx}{dt}\right)^{2} + \left(\frac{dy}{dt}\right)^{2}} \; dt$$
그리고 미적분학 - 미적분학 기본정리의 내용도 복습해보도록 하겠습니다. 미적분학 기본정리는 쉽게 설명하면 미분과 적분 사이의 관계를 설명하는 정리입니다. 두 개의 정리로 이루어져 있으면 특히 오늘은 두번째 정리에 대해서 집중해보도록 하겠습니다. 함수 $F(x)$를 $f(x)$의 적분함수라고 하겠습니다.
$$\int_{a}^{b} f(x) \; dx = F(b) - F(a)$$
이때, 피적분함수 $f(x)$는 닫힌 구간 $[a, b]$에서 연속함수입니다. 위 정리에 따르면 $f(x) = F^{'}(x)$이기 때문에 아래와 같이 쓸 수 있겠죠.
$$\int_{a}^{b} F^{'}(x) \; dx = F(b) - F(a)$$
즉, 미분된 함수를 구간 $[a, b]$에서 적분한다는 것은 기존 함수 $F(x)$의 윗끝 값에서 아랫끝 값을 빼주면 되는 것입니다. 이를 다변수 함수로 어떻게 확장할 수 있을까요? 미적분학 - 기울기벡터에서는 다변수 함수에서의 미분인 기울기벡터를 계산하는 방법을 알려주고 있습니다. 따라서, 저희는 단변수 함수에 대한 미적분학 기본정리를 다변수 함수로 확장할 때 기울기벡터를 사용하면 된다는 것을 알 수 있죠.
정리1.
곡선 $C$를 $a \le t \le b$에서 벡터함수 $\mathbf{r}(t)$의 부드러운 곡선이라고 하자. 그리고 함수 $f$를 미분가능한 다변수 함수로 기울기벡터 $\nabla f$가 곡선 $C$에서 연속인 함수라고 할 때, 다변수 함수의 곡선 $C$에서의 선적분에 대한 미적분학 기본정리는 아래와 같다.
$$\int_{C} \nabla f \cdot d\mathbf{r} = f(\mathbf{r}(b)) - f(\mathbf{r}(a))$$
증명
$$\begin{align*} \int_{C} \nabla f \cdot d \mathbf{r} &= \int_{a}^{b} \nabla f(\mathbf{r}(a)) \cdot \mathbf{r}^{'}(t) \; dt \\ &= \int_{a}^{b} \left(\frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt} + \frac{\partial f}{\partial z} \frac{dz}{dt}\right) \; dt \\ &= \int_{a}^{b} \frac{d}{dt} f(\mathbf{r}(t)) \; dt \\ &= f(\mahtbf{r}(a)) - f(\mathbf{r}(b))\end{align*}$$
설명

위 정리는 곡선 $C$에서 다변수 함수의 기울기벡터에 대한 선적분을 수행할 때 오직 시점 $A$와 종점 $B$만 신경쓰면 된다는 것을 알려주고 있습니다. 예를 들어, 이차원 곡선 $C$에서는 아래와 같은 결과를 얻을 수 있습니다.
$$\int_{C} \nabla f \cdot d\mathbf{r} = f(\mathbf{r}(b)) - f(\mathbf{r}(a)) = f(x_{1}, y_{1}) - f(x_{2}, y_{2})$$
그리고 삼차원 곡선에는 아래와 같은 결과를 얻을 수 있죠.
$$\int_{C} \nabla f \cdot d\mathbf{r} = f(\mathbf{r}(b)) - f(\mathbf{r}(a)) = f(x_{1}, y_{1}, z_{1}) - f(x_{2}, y_{2}, z_{2})$$
위와 같이 어떠한 곡선의 경로에 관계없이 단순히 곡선의 시점과 종점에만 의존하는 선적분을 경로의 독립성(independence of path)라고 합니다. 또한, 이를 포함하는 벡터장인 $D$를 보존장(conservative vector field)라고 합니다. 다음으로 저희가 고려해볼것은 임의의 벡터함수 $\mathbf{F}$에 대해서도 경로의 독립성이 성립할 수 있을지에 대한 의문입니다.
정리2.
정의역 $D$에서 정의된 벡터함수 $\mathbf{F}$가 있다고 하자. 정의역 $D$에서 $\int_{C} \mathbf{F} \cdot d\mathbf{r}$이 경로에 대해 독립적인 것은 정의역 $D$ 내의 임의의 폐곡선(closed curve) $C$에 대해서 $\int_{C} \mathbf{F} \cdot d\mathbf{r} = 0$과 동치이다.
설명

정리2을 이해하기 위해서는 폐곡선(closed curve)에 대한 개념부터 이해해야합니다. 폐곡선이란 곡선 중 시점과 종점이 동일한 곡선으로 $\mathbf{r}(a) = \mathbf{r}(b)$인 곡선을 의미합니다.

먼저, 정리2을 증명하기 위해 정의역 $D$에서 정의된 벡터함수 $\mathbf{F}$가 있다고 가정하겠습니다. 그리고 임의의 폐곡선 $C$가 정의역 $D$에서 정의되었다고 가정하죠. 저희는 폐곡선 $C$에서 임의의 2개 점 $A$와 $B$를 선택하도록 하겠습니다. 그러면 위와 같이 점 $A$와 $B$가 찍히겠죠. 여기서 저희는 점 $A$에서 $B$로의 곡선을 $C_{1}$이라고 하고, 점 $B$에서 $A$로의 곡선을 $C_{2}$라고 하겠습니다.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} + \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} - \int_{-C_{2}} \cdot d\mathbf{r} \\ &= 0\end{align*}$$
여기서 저희는 미적분학 - 선적분에서 곡선 $C$를 부드러운 곡선 $C_{1}$와 $C_{2}$로 쪼갰을 때 각 곡선에 대한 선적분의 결과를 합한다는 결과를 먼저 적용하였습니다. 그리고 $-C_{2}$를 $C_{2}$의 방향을 반대로 바뀐 곡선이라고 정의했을 때 $C_{1}$과 $-C_{2}$는 동일한 시점과 종점을 공유하게 됩니다. 이때, $\int_{C} \mathbf{F} \cdot d\mathbf{r}$이 경로에 대해서 독립적이라고 하였기 때문에 $\int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} = \int_{-C_{2}} \mathbf{F} \cdot d\mathbf{r}$이 성립합니다. 따라서, $\int_{C} \mathbf{F} \cdot d\mathbf{r} = 0$이 되는 것이죠.
이번에는 반대로 증명해보겠습니다. 일단, 벡터함수 $\mathbf{F}$가 정의된 정의역 $D$의 임의의 곡선 $C$에 대해서 $\int_{C} \mathbf{F} \cdot d\mathbf{r} = 0$이라고 하겠습니다. 저희는 임의의 점 $A$와 $B$를 선택한 뒤 두 점 사이의 임의의 2개의 경로 $C_{1}$과 $C_{2}$가 존재한다고 가정하겠습니다. 그리고 곡선 $C$는 두 곡선 $C_{1}$과 $-C_{2}$가 이어진 것으로 고려한다고 하죠.
$$\begin{align*} 0 &= \int_{C} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} + \int_{-C_{2}} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} - \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \\ \Rightarrow& \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} = \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \end{align*}$$
위 수식의 마지막 결론은 시점과 종점이 동일한 임의의 두 곡선 $C_{1}$와 $C_{2}$에 대한 선적분을 수행할 때 동일한 결과를 준다는 것입니다. 따라서, 경로에 대해서 무관하다는 뜻이 되겠네요.
정리3.
벡터함수 $\mathbf{F}$를 연결된(connected) 열린(open) 영역 $D$에서 연속인 벡터장이라고 가정하자. 만약, $\int_{C} \mathbf{F} \cdot d\mathbf{r}$이 영역 $D$에서 경로에 무관하다고 할 때 $\mathbf{F}$는 영역 $D$에서 보존장이며 이는 $\nabla f = \mathbf{F}$를 만족하는 함수 $f$가 존재함을 의미한다.
설명
정리3을 증명하기 위해 영역 $D$에서 고정점(fixed point) $A(a, b)$를 선택하겠습니다. 그리고 저희의 목표는 $\nabla f = \mathbf{F}$를 만족하는 함수 $f$가 존재함을 보여야하기 때문에 저희가 원하는 퍼텐셜 함수 $f$를 영역 $D$에서 임의의 점 $(x, y)$에 대해서 아래와 같이 정의하도록 하겠습니다.
$$f(x, y) = \int_{(a, b)}^{(x, y)} \mathbf{F} \cdot d\mathbf{r}$$
이때, 정리3의 조건에 의해 $\int_{C} \mathbf{F} \cdot d\mathbf{r}$이 영역 $D$에서 경로에 무관하기 때문에 $f(x, y)$를 얻기 위해 점 $(a, b)$에서 $(x, y)$의 어떠한 경로 $C$를 선택해도 상관없습니다.

또한 영역 $D$가 연결된 열린 영역이라는 조건을 가지고 있기 때문에 위 그림과 같이 점 $(x, y)$를 중심으로 하고 영역 $D$에 포함되는 열린 디스크를 잡을 수 있습니다. 저희는 열린 디스크의 내부에서 $x_{1} < x$를 만족하는 임의의 점 $(x_{1}, y)$를 선택하도록 하겠습니다. 그리고 곡선 $C_{1}$을 점 $(a, b)$에서 점 $(x_{1}, y)$로의 경로, $C_{2}$를 점 $(x_{1}, y)$에서 $(x, y)$로의 경로라고 정의하고 곡선 $C$는 두 곡선 $C_{1}$과 $C_{2}$의 합집합이라고 정의하겠습니다. 따라서, 저희는 퍼텐셜 함수 $f(x, y)$를 아래와 같이 계산할 수 있죠.
$$\begin{align*} f(x, y) &= \int_{(a, b)}^{(x, y)} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{C_{1}} \mathbf{F} \cdot d\mathbf{r} + \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{(a, b)}^{(x_{1}, y)} \mathbf{F} \cdot d\mathbf{r} + \int_{C_{2}} \mathbf{F} \cdot d\mathbf{r} \end{align*}$$
이때, 위 식에서 첫번째 적분은 $x$에 무관하기 때문에 $x$에 대해서 편미분하면 0이 됩니다.
$$\frac{\partial f}{\partial x} = 0 + \frac{\partial }{\partial x} \int_{C_{2}} \mathbf{F} \cdot \mathbf{r}$$
또한, $\mathbf{F}$가 벡터함수이기 때문에 $P(x, y)$와 $Q(x, y)$에 대해서 $\mathbf{F} = P\mathbf{i} + Q\mathbf{j}$이기 때문에 $\int_{C_{2}} \mathbf{F} \cdot \mathbf{r} = \int_{C_{2}} P \; dx + Q \; dy$가 됩니다. 여기서, 주의해야할 점은 $C_{2}$ 상에서 $y$는 변하지 않는 상수입니다. 따라서, $dy = 0$이죠. 이제, $x_{1} \le t \le x$를 만족하는 매개변수 $t$를 정의하게 되면 미적분학 기본정리를 적용해서 저희는 아래의 식을 얻을 수 있습니다.
$$\begin{align*} \frac{\partial f}{\partial x} &= 0 + \frac{\partial }{\partial x} \int_{C_{2}} \mathbf{F} \cdot \mathbf{r} \\ &= \frac{\partial }{\partial x}\int_{C_{2}} P \; dx + Q \; dy \\ &= \frac{\partial }{\partial x} \int_{x_{1}}^{x} P(t, y) \; dt \\ &= P(x, y) \end{align*}$$
이와 동일한 방식으로 $y_{1} < y$를 만족하는 임의의 점 $(x, y_{1})$를 선택한 뒤 진행하면 $y$에 대한 $f(x, y)$의 편미분 결과도 얻을 수 있습니다.
$$\begin{align*} \frac{\partial f}{\partial y} &= \frac{\partial }{\partial y}\int_{C_{2}} P \; dx + Q \; dy \\ &= \frac{\partial }{\partial y} \int_{y_{1}}^{y} Q(x, t) \; dt \\ &= Q(x, y) \end{align*}$$
따라서, 저희는 아래와 같은 결과를 얻을 수 있습니다.
$$\mathbf{F} = P\mathbf{i} + Q\mathbf{j} = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} = \nabla f$$
이는 곧 벡터장 $\mathbf{F}$가 보존장임을 의미하기 때문에 정리3은 증명됩니다.
정리4.
벡터함수 $\mathbf{F}(x, y) = P(x, y) \mathbf{i} + Q(x, y) \mathbf{j}$가 보존장이고 $P$와 $Q$가 정의역 $D$에서 연속 편도함수를 가진다고 할 때 $\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$가 성립한다.
설명

정리4는 영역 $D$가 특별한 타입일 때만 성립하는 정리입니다. 이를 설명하기 위해 단순 곡선(simple curve)에 대한 개념을 이해해야합니다. 단순 곡선이란 쉽게 말해 전혀 꼬여있지 않은 곡선을 의미합니다. 위 그림에서는 아래의 왼쪽 그림이 되겠네요.
정리5.
열린 단순 연결 영역 $D$에서 정의된 벡터함수 $\mathbf{F}(x, y) = P(x, y) \mathbf{i} + Q(x, y) \mathbf{j}$가 있다고 가정하자. 영역 $D$에서 함수 $P$와 $Q$가 연속인 편도함수를 가지고 $\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$가 성립한다고 할 때 벡터장 $\mathbf{F}$는 보존장이다.
설명

정리5를 이해하기 위해 더 강력한 조건을 가진 영역 $D$의 모양을 이해할 필요가 있습니다. 단순 연결 영역이라는 것은 위의 그림과 같이 중간이 구멍이 없으며 끊어지지 않은 영역을 의미합니다. 위 영역에서 정의된 벡터장 $\mathbf{F}$가 보존장일 조건에 대해서 설명하는 정리이죠. 위 정리는 앞으로 저희가 배울 가장 중요한 정리인 그린 정리(Green's Theorem)의 기초가 되기 때문에 알아두시는 것이 중요합니다.
예제1. 벡터장 $\mathbf{F}(x, y) = (x - y) \mathbf{i} + (x - 2) \mathbf{j}$가 보존장인지 아닌지 결정하라.
$P(x, y) = x - y$ 그리고 $Q(x, y) = x - 2$라고 하자. 그러면 $\frac{\partial P}{\partial y} = -1$이고 $\frac{\partial Q}{\partial x} = 1$이기 때문에 두 편도함수가 갔지 않으므로 벡터장 $\mathbf{F}$는 보존장이 아니다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 회전과 발산 (0) | 2022.07.26 |
|---|---|
| 미적분학 - 그린 정리 (0) | 2022.07.25 |
| 미적분학 - 선적분 (0) | 2022.07.15 |
| 미적분학 - 벡터장 (0) | 2022.07.13 |
| 미적분학 - 다중적분의 변수변환법 (0) | 2022.07.11 |
