안녕하세요. 지난 포스팅의 미적분학 - 곡선의 법선벡터와 종법선벡터에서는 곡선을 통해 얻을 수 있는 두 가지 종류의 벡터(법선벡터 / 종법선벡터)의 정의와 단위 기울기 벡터, 법선벡터, 종법선벡터를 얻을 수 있는 두 가지 종류의 평면(법평면 / 접촉평면)에 대해서 알아보았습니다. 지금까지 저희는 단변수 함수 $f(x)$의 형태만 보았지만 오늘부터는 여러 개의 변수를 가지는 다변수 함수(multi-variable function)에 대해서 알아보도록 하겠습니다.
정의1. 다변수 함수(multi-variable function)
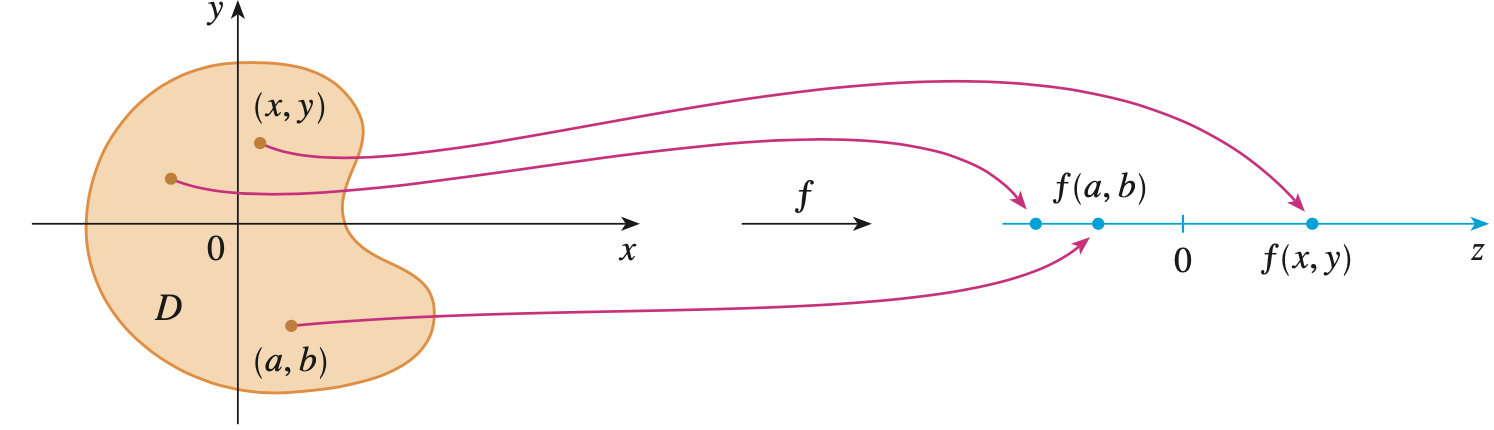
다변수 함수는 어떤 집합 $D$에 대해서 실수쌍 $(x, y) \in D$을 고유한 규칙으로 값 $f(x, y)$를 배정하는 규칙이다. 이때, 집합 $D$는 함수 $f$의 정의역(domain), 집합 $R=\{f(x, y) | (x, y) \in D\}$는 치역(range)이다. 또한, $z = f(x, y)$라고 했을 때 $x, y$를 독립변수(independent variable)이라고 하고, $z$를 종속변수(dependent variable)이라고 한다.
예제1. 함수 $f(x, y) = \frac{\sqrt{x + y + 1}}{x - 1}$에 대해서 $f(3, 2)$를 구하고 함수 $f$의 정의역을 구하여라.
$$f(3, 2) = \frac{\sqrt{3 + 2 + 1}}{3 - 1} = \frac{\sqrt{6}}{2}$$
주어진 함수는 유리함수이기 때문에 분모가 0이 되는 영역은 정의역이 될 수 없다. 따라서, $D_{1} =\{(x, y) | x \neq 1\}$인 영역을 얻을 수 있다. 또한, 분자가 무리함수이기 때문에 항상 무리함수가 정의되기 위해 0과 같거나 실수여야 한다. 따라서, $D_{2} = \{(x, y) | x + y + 1 \ge 0 \}$을 얻을 수 있다. 함수 $f$의 정의역은 두 집합의 교집합으로 정의된다.
$$D = D_{1} \cap D_{2} = \{(x, y) | x + y + 1 \ge 0, x \neq 1\}$$

예제2. 함수 $f(x, y) = x\ln(y^{2} - x)$에 대해서 $f(3, 2)$를 구하고 함수 $f$의 정의역을 구하여라.
$$f(3, 2) = 3\ln(2^{2} - 3) = 3 \ln(1) = 0$$
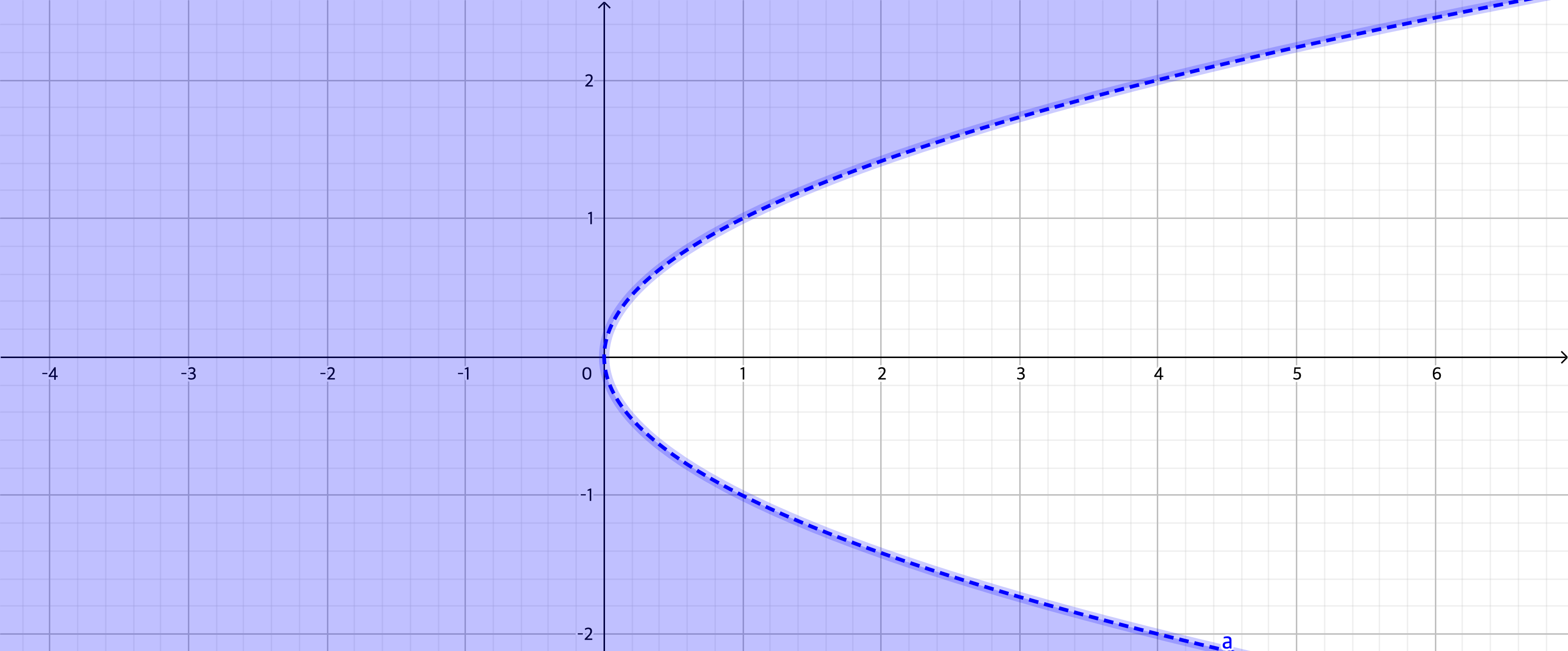
주어진 함수에는 로그함수가 포함되어 있기 때문에 $D = \{(x, y) | y^{2} - x > 0\}$이다.
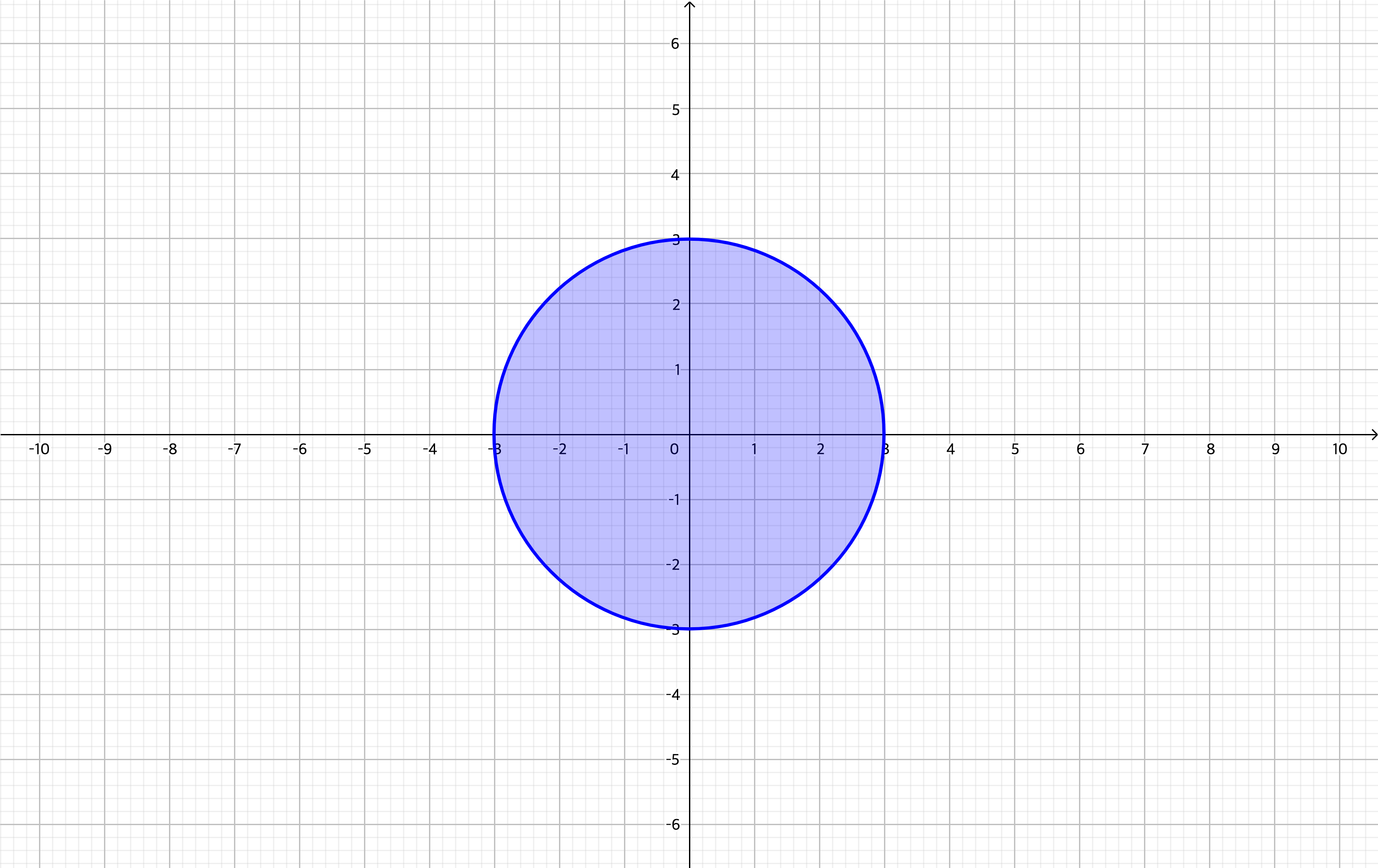
예제3. 함수 $f(x, y) = \sqrt{9 - x^{2} - y^{2}}$에 대해서 $f(2, 2)$를 구하고 함수 $f$의 정의역을 구하여라.
$$f(3, 2) = \sqrt{9 - 2^{2} - 2^{2} = 1$$
주어진 함수에는 무리함수가 포함되어 있기 때문에 $D = \{(x, y) | x^{2} + y^{2} \le 9\}$이다.
정의2. 그래프(graph)
함수 $f$의 그래프는 순서쌍 $(x, y) \in D$에 대해서 $z = f(x, y) $를 만족하는 모든 $(x, y, z) \in \mathbb{R}^{3}$이다.
예제4. 함수 $f(x, y) = 6 - 3x - 2y$의 그래프를 스케치하라.
정의3. 등고선(level curve)
함수 $f$의 등고선은 상수 $k$에 대해서 $f(x, y) = k$를 만족하는 곡선이다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 편미분 (0) | 2022.06.08 |
|---|---|
| 미적분학 - 다변수 함수의 극한과 연속 (0) | 2022.06.07 |
| 미적분학 - 곡선의 법선벡터와 종법선벡터 (0) | 2022.06.02 |
| 미적분학 - 곡선의 곡률 (0) | 2022.06.01 |
| 미적분학 - 공간곡선의 길이 (0) | 2022.05.31 |

