안녕하세요. 지난 포스팅의 미적분학 - 곡선의 곡률에서는 곡률을 구하는 방법과 이와 관련된 몇 가지 정리에 대해서 알아보았습니다. 오늘은 이어서 곡선의 법선벡터(normal vector)와 종법선벡터(binormal vector)에 대해서 알아보도록 하겠습니다.
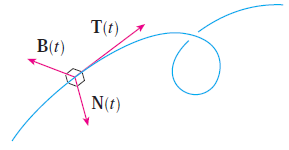
일단, 미적분학 - 벡터의 미분과 적분에서 보았던 단위 기울기 벡터(unit tangent vector)와 함께 보도록 하겠습니다. 기본적으로 법선벡터는 단위 기울기 벡터와 수직을 이루는 벡터를 의미합니다. 그리고 저희는 단위 기울기 벡터 $\mathbf{T}$와 단위 기울의 벡터의 미분인 $\mathbf{T}^{'}$가 서로 직교(orthogonal)한다는 사실을 알고 있기 때문에 법선벡터 $\mathbf{N}(t) = \frac{\mathbf{T}^{'}(t)}{|\mathbf{T}^{'}(t)|}$라고 할 수 있습니다.
그리고 종법선벡터는 법선벡터와 단위 기울기 벡터에 모두 수직인 벡터로 이는 $\mathbf{N}$과 $\mathbf{T}$의 외적을 통해 구할 수 있습니다.
$$\mathbf{B}(t) = \mathbf{T}(t) \times \mathbf{N}(t)$$
정의1. 법선벡터(normal vector)와 종법선벡터(binormal vector)
법선벡터 $\mathbf{N}$은 단위 기울기 벡터 $\mathbf{T}$와 수직을 이루는 벡터로 단위 기울기 벡터의 미분으로 정의된다.
$$\mathbf{N}(t) = \frac{\mathbf{T}^{'}(t)}{|\mathbf{T}^{'}(t)|}$$
종법선벡터 $\mathbf{B}$는 법선벡터 $\mathbf{N}$과 단위 기울기 벡터 $\mathbf{T}$와 동시에 수직을 이루는 벡터로 두 벡터의 외적으로 정의된다.
$$\mathbf{B}(t) = \mathbf{T}(t) \times \mathbf{N}(t)$$
예제1. 벡터함수 $\mathbf{r}(t) = <\cos(t), \sin(t), t>$의 단위 기울기 벡터, 법선벡터, 종법선벡터를 구하여라.
먼저 단위 기울기 벡터를 구하기 위해 벡터함수의 미분을 구한다.
$$\mathbf{r}^{'}(t) = <-\sin(t), \cos(t), 1>$$
$$\mathbf{T}(t) = \frac{\mathbf{r}^{'}(t)}{|\mathbf{r}^{'}(t)|} = \frac{1}{\sqrt{2}}<-\sin(t), \cos(t), 1>$$
$$\mathbf{T}^{'}(t) = \frac{1}{\sqrt{2}}<-\cos(t), -\sin(t), 0>$$
$$\mathbf{N}(t) = \frac{\mathbf{T}^{'}(t)}{|\mathbf{T}^{'}(t)|} = <-\cos(t), -\sin(t), 0>$$
$$\begin{align*} \mathbf{B}(t) &= \mathbf{T}(t) \times \mathbf{N}(t) \\ &= \begin{vmatrix} \mathbf{i} &
\mathbf{j} & \mathbf{k} \\ -\sin(t) & \cos(t) & 1 \\ -\cos(t) & -\sin(t) & 0 \\ &= \frac{1}{\sqrt{2}}<\sin(t), \-\cos(t), 1> \end{vmatrix}\end{align*}$$
정의2. 법평면(normal plane)와 접촉평면(osculating plane)
법선벡터 $\mathbf{N}$와 종법선벡터 $\mathbf{B}$에 의해 결정되는 평면을 법평면이라 하고 단위 기울기 벡터 $\mathbf{T}$와 법선벡터 $\mathbf{N}$에 의해 결정되는 평면을 접촉평면이라 한다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 다변수 함수의 극한과 연속 (0) | 2022.06.07 |
|---|---|
| 미적분학 - 다변수 함수 (0) | 2022.06.06 |
| 미적분학 - 곡선의 곡률 (0) | 2022.06.01 |
| 미적분학 - 공간곡선의 길이 (0) | 2022.05.31 |
| 미적분학 - 벡터함수의 미분과 적분 (2) | 2022.05.30 |
