안녕하세요. 지난 포스팅의 미적분학 - 공간곡선의 길이에서는 벡터함수를 매개변수 방정식으로 생각한 뒤 곡선의 길이를 구하는 공식을 유도해보았습니다. 결과적으로 $a \le t \le b$에서 정의된 벡터함수 $\mathbf{r}(t)$의 곡선의 길이는 $L = \int_{a}^{b} \mathbf{r}^{'}(t) \; dt$입니다. 오늘은 곡률(curvature)의 정의에 대해서 알아보도록 하겠습니다.
정의1. 곡률(curvature)
곡선의 곡률은 $\kappa = \left|\frac{d\mathbf{T}}{ds}\right|$로 정의되고 이때, $\mathbf{T}$는 단위 기울기 벡터이다.
설명
기본적으로 구간 $I$에서 공간곡선 $\mathbf{r}$이 부드럽다(smooth)는 것은 구간 $I$에서 $\mathbf{r}^{'}$이 연속이고 $\mathbf{r}^{'} \neq 0$이라는 것을 의미합니다. 이때, 부드러운 곡선은 뾰족한 지점을 가지지 않고 모든 점에서 부드럽게 진행됩니다. 따라서, 곡선의 임의의 점에 대해서 해당 곡선이 얼마나 휘어있는 지에 대한 정보를 표현할 수 있습니다.
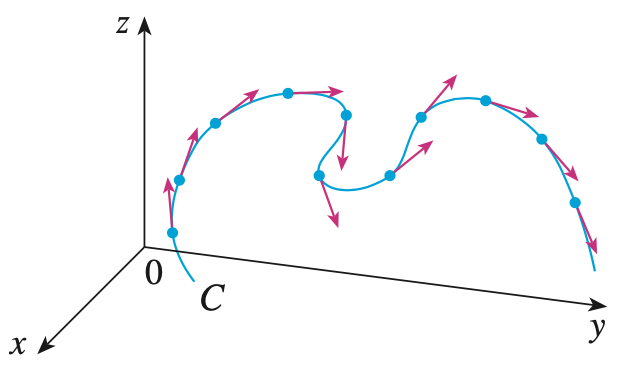
곡률에 대해서 설명하기 위해서 위 그림을 보도록 하겠습니다. 위 그림을 보시면 곡선 $C$가 어느정도 완만하게 변할 때는 해당 점에서의 기울기 벡터 역시 크게 변하지 않습니다. 그와는 다르게 $C$가 많이 변하면 기울기 벡터 역시 크게 변하게 되죠. 따라서, 저희는 곡률을 기울기 벡터의 변화율로 정의할 수 있는 것입니다. 단, 저희는 곡선을 따라서 진행되어야하기 때문에 곡선의 길이를 차분해야합니다. 위의 정의에서 보았던 $s$가 곡선의 길이에 대한 함수로써 아래와 같이 정의됩니다.
$$s(t) = \int_{a}^{t} \left|\mathbf{r}^{'}(u)\right| \; du = \int_{a}^{t} \sqrt{\left(\frac{dx}{du}\right)^{2} + \left(\frac{dy}{du}\right)^{2} + \left(\frac{dz}{du}\right)^{2}}$$
여기서, 다시 정의로 돌아와서 저희는 연쇄 법칙을 이용해서 정의를 다시 쓸 수 있습니다.
$$\kappa = \left|\frac{d\mathbf{T}}{ds}\right| = \left|\frac{d\mathbf{T}/dt}{ds/dt}\right| = \frac{|\mathbf{T}^{'}(t)|}{|\mathbf{r}^{'}(t)|}$$
따라서, 저희는 좀 더 쉽게 임의의 곡선에 대한 곡률을 구할 수 있게 되었습니다.
예제1. 공간곡선 $\mathbf{r}(t) = <a\cos(t), a\sin(t)>$의 곡률을 구하여라.
$\mathbf{r}^{'}(t) = <-a\sin(t), a\cos(t)>$이고 $\mathbf{T}^{'}(t) = \frac{\mathbf{r}^{'}(t)}{\left|\mathbf{r}^{'}(t)\right|} = <-\sin(t), \cos(t)>$이다. 따라서, 주어진 공간곡선 $\mathbf{r}$의 곡률은 아래와 같다.
$$\begin{align*} \kappa &= \left|\frac{\mathbf{T}^{'}(t)}{\left|\mathbf{r}^{'}(t)\right|}\right| \\ &= \frac{1}{a} \end{align*}$$
위 예제를 통해서 반지름이 $a$인 원의 곡률은 항상 $\kappa = \frac{1}{a}$임을 알 수 있습니다. 하지만, 정의를 이용하는 방식은 단위 기울기 벡터 $\mathbf{T}$를 구해야한다는 점에서 조금 귀찮을 수 있습니다. 따라서, 좀 더 쉽게 계산하는 방법이 존재합니다.
정리1.
벡터함수 $\mathbf{r}$의 곡률은 $\kappa = \frac{|\mathbf{r}^{'}(t) \times \mathbf{r}^{''}(t)|}{|\mathbf{r}^{'}(t)|^{3}}$이다.
증명
미적분학 - 벡터함수의 미분과 적분에서 단위 기울기 벡터의 정의에 의해 $\mathbf{T}(t) = \frac{\mathbf{r}^{'}(t)}{|\mathbf{r}^{'}(t)|}$이고 미적분학 - 공간곡선의 길이에서 곡선의 길이의 정의에 의해 $|\mathbf{r}^{'}| = \frac{ds}{dt}$이다.
$$\mathbf{r}^{'} = \mathbf{T} |\mathbf{r}^{'}| = \mathbf{T} \frac{ds}{dt}$$
이때, 미분규칙에 의해서 벡터함수 $\mathbf{r}^{''}$의 이계도함수를 구할 수 있다.
$$\mathbf{r}^{''} = \frac{d^{2}s}{dt^{2}} \mathbf{T} + \frac{ds}{dt} \mathbf{T}^{'}$$
한편, 미적분학 - 벡터의 외적에서 동일한 벡터의 외적은 영벡터($\mathbf{0}$)이라는 사실을 통해 $\mathbf{T} \times \mathbf{T} = \mathbf{0}$임을 알 수 있다. 따라서, $\mathbf{r}^{'}$와 $\mathbf{r}^{''}$ 사이의 외적을 쉽게 구할 수 있다.
$$\mathbf{r}^{'} \times \mathbf{r}^{''} = \frac{ds}{dt} \mathbf{T} \left(\frac{d^{2}s}{dt^{2}} \mathbf{T} + \frac{ds}{dt} \mathbf{T}^{'} \right) = \left(\frac{ds}{dt}\right)^{2} \left(\mathbf{T} \times \mathbf{T}^{'}\right)$$
이때, 모든 $t$에 대해서 $\left|\mathbf{T}(t)\right| = 1$이고 $\mathbf{T}$와 $\mathbf{T}^{'}$가 서로 직교한다는 사실을 이용하여 식을 추가적으로 정리한다.
$$\begin{align*} \left|\mathbf{r}^{'} \times \mathbf{r}^{''}\right| &= \left(\frac{ds}{dt}\right)^{2} \left|\mathbf{T} \times \mathbf{T}^{'}\right| \\ &= \left(\frac{ds}{dt}\right)^{2} |\mathbf{T}||\mathbf{T}^{'}| \\ &= \left(\frac{ds}{dt}\right)^{2} |\mathbf{T}^{'}|\end{align*}$$
따라서, $\mathbf{T}^{'} = \frac{|\mathbf{r}^{'} \times \mathbf{r}^{''}|}{\left(ds / dt\right)^{2}} = \frac{|\mathbf{r}^{'} \times \mathbf{r}^{''}|}{|\mathbf{r}^{'}|^{2}}$임을 알 수 있다. 이때, $\mathbf{T}^{'}$를 곡률 공식에 대입하여 마무리한다.
$$\kappa = \frac{|\mathbf{T}^{'}|}{|\mathbf{r}^{'}|} = \frac{|\mathbf{r}^{'} \times \mathbf{r}^{''}|}{|\mathbf{r}^{'}|^{3}}$$
예제1. 벡터함수 $\mathbf{r}(t) = <t, t^{2}, t^{3}>$의 곡률을 $t$로 표현하라.
벡터함수 $\mathbf{r}$의 곡률을 표현하기 위해 벡터함수 $\mathbf{r}$의 일계도함수와 이계도함수를 구한다.
$$\mathbf{r}^{'}(t) = <1, 2t, 3t^{2}>$$
$$\mathbf{r}^{''}(t) = <0, 2, 6t>$$
여기서, $|\mathbf{r}^{'}| = \sqrt{1 + 4t^{2} + 9t^{4}}$이다. 그리고 $|\mathbf{r}^{'} \times \mathbf{r}^{''}|$을 계산하기 위해 두 도함수 사이의 외적을 계산한다.
$$\begin{align*} \mathbf{r}^{'} \times \mathbf{r}^{''} &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2t & 3t^{2} \\ 0 & 2 & 6t \end{vmatrix} \\ &= <6t^{2}, -6t, 2>\end{align*}$$
다음으로 외적의 크기를 계산한다.
$$|\mathbf{r}^{'} \times \mathbf{r}^{''}| = \sqrt{36t^{4} + 36t^{2} + 4} = 2\sqrt{9t^{4} + 9t^{2} + 1}$$
마지막으로 주어진 벡터함수의 곡률을 정리1에 대입하여 계산한다.
$$\kappa(t) = \frac{|\mathbf{r}^{'} \times \mathbf{r}^{''}|}{|\mathbf{r}^{'}|^{3}} = \frac{2\sqrt{9t^{4} + 9t^{2} + 1}}{\left(1 + 4t^{2} + 9t^{4}\right)^{3/2}}$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 다변수 함수 (0) | 2022.06.06 |
|---|---|
| 미적분학 - 곡선의 법선벡터와 종법선벡터 (0) | 2022.06.02 |
| 미적분학 - 공간곡선의 길이 (0) | 2022.05.31 |
| 미적분학 - 벡터함수의 미분과 적분 (2) | 2022.05.30 |
| 미적분학 - 벡터함수와 공간곡선 (0) | 2022.05.28 |
안녕하세요. 지난 포스팅의 미적분학 - 공간곡선의 길이에서는 벡터함수를 매개변수 방정식으로 생각한 뒤 곡선의 길이를 구하는 공식을 유도해보았습니다. 결과적으로 a≤t≤b에서 정의된 벡터함수 r(t)의 곡선의 길이는 L=∫bar′(t)dt입니다. 오늘은 곡률(curvature)의 정의에 대해서 알아보도록 하겠습니다.
정의1. 곡률(curvature)
곡선의 곡률은 κ=|dTds|로 정의되고 이때, T는 단위 기울기 벡터이다.
설명
기본적으로 구간 I에서 공간곡선 r이 부드럽다(smooth)는 것은 구간 I에서 r′이 연속이고 r′≠0이라는 것을 의미합니다. 이때, 부드러운 곡선은 뾰족한 지점을 가지지 않고 모든 점에서 부드럽게 진행됩니다. 따라서, 곡선의 임의의 점에 대해서 해당 곡선이 얼마나 휘어있는 지에 대한 정보를 표현할 수 있습니다.

곡률에 대해서 설명하기 위해서 위 그림을 보도록 하겠습니다. 위 그림을 보시면 곡선 C가 어느정도 완만하게 변할 때는 해당 점에서의 기울기 벡터 역시 크게 변하지 않습니다. 그와는 다르게 C가 많이 변하면 기울기 벡터 역시 크게 변하게 되죠. 따라서, 저희는 곡률을 기울기 벡터의 변화율로 정의할 수 있는 것입니다. 단, 저희는 곡선을 따라서 진행되어야하기 때문에 곡선의 길이를 차분해야합니다. 위의 정의에서 보았던 s가 곡선의 길이에 대한 함수로써 아래와 같이 정의됩니다.
s(t)=∫ta|r′(u)|du=∫ta√(dxdu)2+(dydu)2+(dzdu)2
여기서, 다시 정의로 돌아와서 저희는 연쇄 법칙을 이용해서 정의를 다시 쓸 수 있습니다.
κ=|dTds|=|dT/dtds/dt|=|T′(t)||r′(t)|
따라서, 저희는 좀 더 쉽게 임의의 곡선에 대한 곡률을 구할 수 있게 되었습니다.
예제1. 공간곡선 r(t)=<acos(t),asin(t)>의 곡률을 구하여라.
r′(t)=<−asin(t),acos(t)>이고 T′(t)=r′(t)|r′(t)|=<−sin(t),cos(t)>이다. 따라서, 주어진 공간곡선 r의 곡률은 아래와 같다.
κ=|T′(t)|r′(t)||=1a
위 예제를 통해서 반지름이 a인 원의 곡률은 항상 κ=1a임을 알 수 있습니다. 하지만, 정의를 이용하는 방식은 단위 기울기 벡터 T를 구해야한다는 점에서 조금 귀찮을 수 있습니다. 따라서, 좀 더 쉽게 계산하는 방법이 존재합니다.
정리1.
벡터함수 r의 곡률은 κ=|r′(t)×r″(t)||r′(t)|3이다.
증명
미적분학 - 벡터함수의 미분과 적분에서 단위 기울기 벡터의 정의에 의해 T(t)=r′(t)|r′(t)|이고 미적분학 - 공간곡선의 길이에서 곡선의 길이의 정의에 의해 |r′|=dsdt이다.
r′=T|r′|=Tdsdt
이때, 미분규칙에 의해서 벡터함수 r″의 이계도함수를 구할 수 있다.
r″=d2sdt2T+dsdtT′
한편, 미적분학 - 벡터의 외적에서 동일한 벡터의 외적은 영벡터(0)이라는 사실을 통해 T×T=0임을 알 수 있다. 따라서, r′와 r″ 사이의 외적을 쉽게 구할 수 있다.
r′×r″=dsdtT(d2sdt2T+dsdtT′)=(dsdt)2(T×T′)
이때, 모든 t에 대해서 |T(t)|=1이고 T와 T′가 서로 직교한다는 사실을 이용하여 식을 추가적으로 정리한다.
|r′×r″|=(dsdt)2|T×T′|=(dsdt)2|T||T′|=(dsdt)2|T′|
따라서, T′=|r′×r″|(ds/dt)2=|r′×r″||r′|2임을 알 수 있다. 이때, T′를 곡률 공식에 대입하여 마무리한다.
κ=|T′||r′|=|r′×r″||r′|3
예제1. 벡터함수 r(t)=<t,t2,t3>의 곡률을 t로 표현하라.
벡터함수 r의 곡률을 표현하기 위해 벡터함수 r의 일계도함수와 이계도함수를 구한다.
r′(t)=<1,2t,3t2>
r″(t)=<0,2,6t>
여기서, |r′|=√1+4t2+9t4이다. 그리고 |r′×r″|을 계산하기 위해 두 도함수 사이의 외적을 계산한다.
r′×r″=|ijk12t3t2026t|=<6t2,−6t,2>
다음으로 외적의 크기를 계산한다.
|r′×r″|=√36t4+36t2+4=2√9t4+9t2+1
마지막으로 주어진 벡터함수의 곡률을 정리1에 대입하여 계산한다.
κ(t)=|r′×r″||r′|3=2√9t4+9t2+1(1+4t2+9t4)3/2
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 다변수 함수 (0) | 2022.06.06 |
|---|---|
| 미적분학 - 곡선의 법선벡터와 종법선벡터 (0) | 2022.06.02 |
| 미적분학 - 공간곡선의 길이 (0) | 2022.05.31 |
| 미적분학 - 벡터함수의 미분과 적분 (2) | 2022.05.30 |
| 미적분학 - 벡터함수와 공간곡선 (0) | 2022.05.28 |
