안녕하세요. 지난 포스팅의 미적분학 - 공간곡선의 길이에서는 벡터함수를 매개변수 방정식으로 생각한 뒤 곡선의 길이를 구하는 공식을 유도해보았습니다. 결과적으로 $a \le t \le b$에서 정의된 벡터함수 $\mathbf{r}(t)$의 곡선의 길이는 $L = \int_{a}^{b} \mathbf{r}^{'}(t) \; dt$입니다. 오늘은 곡률(curvature)의 정의에 대해서 알아보도록 하겠습니다.
정의1. 곡률(curvature)
곡선의 곡률은 $\kappa = \left|\frac{d\mathbf{T}}{ds}\right|$로 정의되고 이때, $\mathbf{T}$는 단위 기울기 벡터이다.
설명
기본적으로 구간 $I$에서 공간곡선 $\mathbf{r}$이 부드럽다(smooth)는 것은 구간 $I$에서 $\mathbf{r}^{'}$이 연속이고 $\mathbf{r}^{'} \neq 0$이라는 것을 의미합니다. 이때, 부드러운 곡선은 뾰족한 지점을 가지지 않고 모든 점에서 부드럽게 진행됩니다. 따라서, 곡선의 임의의 점에 대해서 해당 곡선이 얼마나 휘어있는 지에 대한 정보를 표현할 수 있습니다.
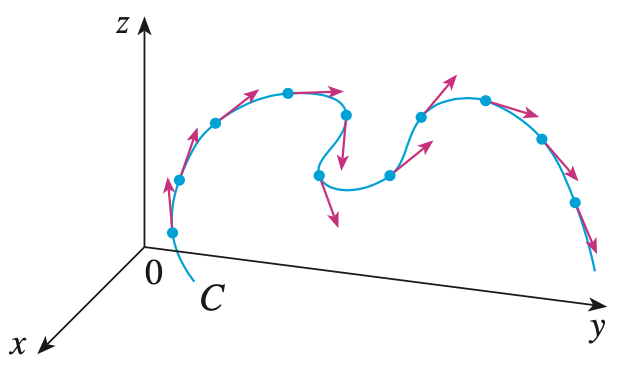
곡률에 대해서 설명하기 위해서 위 그림을 보도록 하겠습니다. 위 그림을 보시면 곡선 $C$가 어느정도 완만하게 변할 때는 해당 점에서의 기울기 벡터 역시 크게 변하지 않습니다. 그와는 다르게 $C$가 많이 변하면 기울기 벡터 역시 크게 변하게 되죠. 따라서, 저희는 곡률을 기울기 벡터의 변화율로 정의할 수 있는 것입니다. 단, 저희는 곡선을 따라서 진행되어야하기 때문에 곡선의 길이를 차분해야합니다. 위의 정의에서 보았던 $s$가 곡선의 길이에 대한 함수로써 아래와 같이 정의됩니다.
$$s(t) = \int_{a}^{t} \left|\mathbf{r}^{'}(u)\right| \; du = \int_{a}^{t} \sqrt{\left(\frac{dx}{du}\right)^{2} + \left(\frac{dy}{du}\right)^{2} + \left(\frac{dz}{du}\right)^{2}}$$
여기서, 다시 정의로 돌아와서 저희는 연쇄 법칙을 이용해서 정의를 다시 쓸 수 있습니다.
$$\kappa = \left|\frac{d\mathbf{T}}{ds}\right| = \left|\frac{d\mathbf{T}/dt}{ds/dt}\right| = \frac{|\mathbf{T}^{'}(t)|}{|\mathbf{r}^{'}(t)|}$$
따라서, 저희는 좀 더 쉽게 임의의 곡선에 대한 곡률을 구할 수 있게 되었습니다.
예제1. 공간곡선 $\mathbf{r}(t) = <a\cos(t), a\sin(t)>$의 곡률을 구하여라.
$\mathbf{r}^{'}(t) = <-a\sin(t), a\cos(t)>$이고 $\mathbf{T}^{'}(t) = \frac{\mathbf{r}^{'}(t)}{\left|\mathbf{r}^{'}(t)\right|} = <-\sin(t), \cos(t)>$이다. 따라서, 주어진 공간곡선 $\mathbf{r}$의 곡률은 아래와 같다.
$$\begin{align*} \kappa &= \left|\frac{\mathbf{T}^{'}(t)}{\left|\mathbf{r}^{'}(t)\right|}\right| \\ &= \frac{1}{a} \end{align*}$$
위 예제를 통해서 반지름이 $a$인 원의 곡률은 항상 $\kappa = \frac{1}{a}$임을 알 수 있습니다. 하지만, 정의를 이용하는 방식은 단위 기울기 벡터 $\mathbf{T}$를 구해야한다는 점에서 조금 귀찮을 수 있습니다. 따라서, 좀 더 쉽게 계산하는 방법이 존재합니다.
정리1.
벡터함수 $\mathbf{r}$의 곡률은 $\kappa = \frac{|\mathbf{r}^{'}(t) \times \mathbf{r}^{''}(t)|}{|\mathbf{r}^{'}(t)|^{3}}$이다.
증명
미적분학 - 벡터함수의 미분과 적분에서 단위 기울기 벡터의 정의에 의해 $\mathbf{T}(t) = \frac{\mathbf{r}^{'}(t)}{|\mathbf{r}^{'}(t)|}$이고 미적분학 - 공간곡선의 길이에서 곡선의 길이의 정의에 의해 $|\mathbf{r}^{'}| = \frac{ds}{dt}$이다.
$$\mathbf{r}^{'} = \mathbf{T} |\mathbf{r}^{'}| = \mathbf{T} \frac{ds}{dt}$$
이때, 미분규칙에 의해서 벡터함수 $\mathbf{r}^{''}$의 이계도함수를 구할 수 있다.
$$\mathbf{r}^{''} = \frac{d^{2}s}{dt^{2}} \mathbf{T} + \frac{ds}{dt} \mathbf{T}^{'}$$
한편, 미적분학 - 벡터의 외적에서 동일한 벡터의 외적은 영벡터($\mathbf{0}$)이라는 사실을 통해 $\mathbf{T} \times \mathbf{T} = \mathbf{0}$임을 알 수 있다. 따라서, $\mathbf{r}^{'}$와 $\mathbf{r}^{''}$ 사이의 외적을 쉽게 구할 수 있다.
$$\mathbf{r}^{'} \times \mathbf{r}^{''} = \frac{ds}{dt} \mathbf{T} \left(\frac{d^{2}s}{dt^{2}} \mathbf{T} + \frac{ds}{dt} \mathbf{T}^{'} \right) = \left(\frac{ds}{dt}\right)^{2} \left(\mathbf{T} \times \mathbf{T}^{'}\right)$$
이때, 모든 $t$에 대해서 $\left|\mathbf{T}(t)\right| = 1$이고 $\mathbf{T}$와 $\mathbf{T}^{'}$가 서로 직교한다는 사실을 이용하여 식을 추가적으로 정리한다.
$$\begin{align*} \left|\mathbf{r}^{'} \times \mathbf{r}^{''}\right| &= \left(\frac{ds}{dt}\right)^{2} \left|\mathbf{T} \times \mathbf{T}^{'}\right| \\ &= \left(\frac{ds}{dt}\right)^{2} |\mathbf{T}||\mathbf{T}^{'}| \\ &= \left(\frac{ds}{dt}\right)^{2} |\mathbf{T}^{'}|\end{align*}$$
따라서, $\mathbf{T}^{'} = \frac{|\mathbf{r}^{'} \times \mathbf{r}^{''}|}{\left(ds / dt\right)^{2}} = \frac{|\mathbf{r}^{'} \times \mathbf{r}^{''}|}{|\mathbf{r}^{'}|^{2}}$임을 알 수 있다. 이때, $\mathbf{T}^{'}$를 곡률 공식에 대입하여 마무리한다.
$$\kappa = \frac{|\mathbf{T}^{'}|}{|\mathbf{r}^{'}|} = \frac{|\mathbf{r}^{'} \times \mathbf{r}^{''}|}{|\mathbf{r}^{'}|^{3}}$$
예제1. 벡터함수 $\mathbf{r}(t) = <t, t^{2}, t^{3}>$의 곡률을 $t$로 표현하라.
벡터함수 $\mathbf{r}$의 곡률을 표현하기 위해 벡터함수 $\mathbf{r}$의 일계도함수와 이계도함수를 구한다.
$$\mathbf{r}^{'}(t) = <1, 2t, 3t^{2}>$$
$$\mathbf{r}^{''}(t) = <0, 2, 6t>$$
여기서, $|\mathbf{r}^{'}| = \sqrt{1 + 4t^{2} + 9t^{4}}$이다. 그리고 $|\mathbf{r}^{'} \times \mathbf{r}^{''}|$을 계산하기 위해 두 도함수 사이의 외적을 계산한다.
$$\begin{align*} \mathbf{r}^{'} \times \mathbf{r}^{''} &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2t & 3t^{2} \\ 0 & 2 & 6t \end{vmatrix} \\ &= <6t^{2}, -6t, 2>\end{align*}$$
다음으로 외적의 크기를 계산한다.
$$|\mathbf{r}^{'} \times \mathbf{r}^{''}| = \sqrt{36t^{4} + 36t^{2} + 4} = 2\sqrt{9t^{4} + 9t^{2} + 1}$$
마지막으로 주어진 벡터함수의 곡률을 정리1에 대입하여 계산한다.
$$\kappa(t) = \frac{|\mathbf{r}^{'} \times \mathbf{r}^{''}|}{|\mathbf{r}^{'}|^{3}} = \frac{2\sqrt{9t^{4} + 9t^{2} + 1}}{\left(1 + 4t^{2} + 9t^{4}\right)^{3/2}}$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 다변수 함수 (0) | 2022.06.06 |
|---|---|
| 미적분학 - 곡선의 법선벡터와 종법선벡터 (0) | 2022.06.02 |
| 미적분학 - 공간곡선의 길이 (0) | 2022.05.31 |
| 미적분학 - 벡터함수의 미분과 적분 (2) | 2022.05.30 |
| 미적분학 - 벡터함수와 공간곡선 (0) | 2022.05.28 |
