안녕하세요. 지난 포스팅의 미적분학 - 미분 개요에서는 접선(Tangent)와 미분(Derivative)에 대해서 알아보았습니다. 오늘은 지난 번에 알아본 미분을 임의의 점으로 확장해보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
정의1. 함수 미분(Function Derivative)
함수 $f$의 임의의 점 $x \in \text{dom}(f)$에서의 함수 미분(Function Derivative)은 극한이 존재한다면 아래와 같이 정의된다.
$$f^{'}(x) = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h}$$
이때, 미분의 기호는 다양하며 아래의 기호들 모두 동일한 의미이다.
$$f^{'}(x) = y^{'} = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx}f(x) = Df(x) = D_{x}f(x)$$
설명
저희는 지난 포스팅에서 미분이랑 함수의 각 점에서 접선의 기울기와 같다는 것을 알게 되었습니다. 다만 차이점은 오늘 포스팅에서는 임의의 점에서의 미분을 구하기 위해 이를 함수와 같이 표현하는 것입니다.(지난 포스팅에서는 하나의 점에서의 기울기를 구하였죠?) 간단한 예제들을 통해 함수 미분의 정의를 이용하여 구하는 방법에 대해서 알아보도록 하겠습니다.
예제1. 함수 $f(x) = x^{3} - x$의 미분 $f^{'}(x)$을 구하여라.
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[(x + h)^{3} - (x + h)\right] - \left(x^{3} - x\right)}{h} \\ &= \lim_{h \rightarrow 0} \frac{x^{3} + 3x^{2}h + 3xh^{2} + h^{3} - x^{3} - x}{h} \\ &= \lim_{h \rightarrow 0} \frac{3x^{2}h + 3xh^{2} + h^{3} - h}{h} \\ &= \lim_{h \rightarrow 0} \left(3x^{2} + 3xh + h^{2} - 1\right) = 3x^{2} - 1\end{align*}$$
예제2. 함수 $f(x) = \sqrt{x}$의 미분 $f^{'}(x)$을 구하여라.
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\sqrt{x + h} - \sqrt{x}}{h} \\ &= \lim_{h \rightarrow 0} \left(\frac{\sqrt{x + h} - \sqrt{x}}{h} \cdot \frac{\sqrt{x+ h} + \sqrt{x}}{\sqrt{x + h} + \sqrt{x}}\right) \\ &= \lim_{h \rightarrow 0} \frac{(x + h) - h}{h(\sqrt{x + h} + \sqrt{x})} \\ &= \lim_{h \rightarrow 0} \frac{1}{\sqrt{x + h} + \sqrt{x}} \\ &= \frac{1}{\sqrt{x} + \sqrt{x}} = \frac{1}{2\sqrt{x}}\end{align*}$$
예제3.함수 $f(x) = \frac{1 - x}{2 + x}$의 미분 $f^{'}(x)$을 구하여라.
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{1 - x - h}{2 + x + h} - \frac{1 - x}{2 + x}}{h} \\ &= \lim_{h \rightarrow 0} \frac{(1 - x - h)(2 + x) - (1 - x)(2 + x + h)}{h(2 + x + h)(2 + x)} \\ &= \lim_{h \rightarrow 0} \frac{(2 - x - 2h - x^{2} - xh) - (2 - x + h - x^{2} - xh)}{h} \\ &= \lim_{h \rightarrow 0} \frac{-3h}{h(2 + x + h)(2 + x)} \\ &= \lim_{h \rightarrow 0} \frac{-3}{(2 + x + h)(2 + x)} = -\frac{3}{(2 + x)^{2}}\end{align*}$$
정의2. 미분가능성(Differentiability)
함수 $f$는 $f^{'}(a)$가 존재하면 $x = a$에서 미분가능(Differentiable)하다. 만약, 함수 $f$가 열린 구간 $ I = (a, b), (a, \infty), (-\infty, b), (-\infty, \infty)$의 모든 점 $x \in I$에서 미분가능하면 구간 $I$에서 미분가능하다.
설명
기본적으로 미분의 정의를 고려해본다면 당연하겠지만 미분이 가능하기 위해서는 해당 점에서 극한이 존재해야합니다. 극한의 존재성에 대한 내용은 제거 해당 포스팅에 정리해놓았으니 보고 오시는 것을 추천드립니다. 요약만 해드리면 아래와 같습니다.
미적분학 - 함수의 극한
안녕하세요. 지난 포스팅의 미적분학 - 접선에서는 어떤 점에서 곡선의 접선을 찾는 근사적인 방법에 대해서 알아보았습니다. 오늘은 이를 명확하게 정의하기 위해서 함수의 극한에 대해서 알
everyday-image-processing.tistory.com
정의2-1. 극한의 존재성
함수 $f$가 $x = a$에서 극한이 존재하기 위해서는 좌극한과 우극한이 동일한 값으로 수렴해야한다.
$$\lim_{x \rightarrow a} f(x) = L \text{ if and only if } \lim_{x \rightarrow a^{-}} f(x) = \lim_{x \rightarrow a^{+}} f(x) = L$$
설명
따라서 저희는 간단한 예시에서 위와 같은 존재성에 대한 정의를 활용하여 실제로 미분이 가능한지 불가능한지 판별해보도록 하겠습니다.
예제4. $f(x) = |x|$는 $x = a$에서 미분가능한가?
불가능하다.
1). $x > 0$이라고 했을 때, $f(x) = |x| = x$이다. 그리고 $x + h > 0$를 만족하는 아주 작은 $h$를 고려하면 $|x + h| = x + h$이다. 따라서, $x > 0$일 때,
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{|x + h| - |x|}{h} \\ &= \lim_{h \rightarrow 0} \frac{x + h - x}{h} = \lim_{h \rightarrow 0} \frac{h}{h} = 1 \end{align*}$$
2). $x < 0$이라고 했을 때, $f(x) = |x| = -x$이다. 그리고 $x + h < 0$를 만족하는 아주 작은 $h$를 고려하면 $|x + h| = -x - h$이다. 따라서, $x < 0$일 때,
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{|x + h| - |x|}{h} \\ &= \lim_{h \rightarrow 0} \frac{-x - h + x}{h} = \lim_{h \rightarrow 0} \frac{-h}{h} = -1 \end{align*}$$
$f(x) = |x|$는 $x = 0$에서 $\lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h}$의 극한값이 존재하지 않기 때문에 $f(x)$는 $x = 0$에서 미분불가능하다.
3.정리
함수 $f$가 $x = a$에서 미분가능하면, 함수 $f$는 $x = a$에서 연속이다.
설명
이 정리의 증명을 해보도록 하겠습니다. 먼저, 지난 포스팅의 미적분학 - 연속함수에서 보았던 연속함수의 정의를 상기해보도록 하겠습니다. 함수 $f$가 $x = a$에서 연속이기 위해서는 $\lim_{x \rightarrow a} f(x) = f(a)$를 만족해야하기 때문에 $f(x) - f(a)$가 $x \rightarrow a$로의 극한을 취할 때 0으로 수렴하는 것을 보여야하죠.
그리고 함수 $f$가 $x = a$에서 미분가능하기 때문에 함수 미분의 정의에 따라서 아래의 극한이 존재하게 됩니다.
$$f^{'}(a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}$$
한편, $f(x) - f(a) = \frac{f(x) - f(a)}{x - a} \cdot (x - a)$이기 때문에 다시 한번 식을 정리하여 쓸 수 있습니다.
$$\begin{align*} \lim_{x \rightarrow a} \left[f(x) - f(a)\right] &= \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a} \cdot (x - a) \\ &= \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a} \cdot \lim_{x \rightarrow a} (x - a) \\ &= f^{'}(a) \cdot 0 = 0 \end{align*}$$
하지만, 저희는 최종적으로 $\lim_{x \rightarrow a} f(x) = f(a)$임을 증명해야하기 때문에 아래와 같은 식조작을 한번 더 해주면 됩니다.
$$\begin{align*} \lim_{x \rightarrow a} f(x) &= \lim_{x \rightarrow a} \left[f(a) + (f(x) -f(a))\right] \\ &= \lim_{x \rightarrow a} f(a) + \lim_{x \rightarrow a} \left[f(x) - f(a)\right] \\ &= f(a) + 0 = f(a) \end{align*}$$
따라서, $\lim_{x \rightarrow a} f(x) = f(a)$을 만족하기 때문에 함수 $f$는 $x = a$에서 연속이다.
정의4. 고계 미분(Higher Derivative)
함수 $f$가 미분가능할 때, 그의 도함수 $f^{'}$의 2차 미분 $f^{''}$은 아래와 같이 정의된다.
$$\frac{d}{dx}\left(\frac{dy}{dx}\right) = \frac{d^{2}y}{dx^{2}}$$
설명
고계 미분은 위에서 설명한 2차 미분뿐만 아니라 3차, 4차, 5차 등 더 높은 차수의 미분까지도 계산될 수 있습니다. 그리고 그 과정은 전부 1차 미분과 동일하게 이어지기 때문에 간단한 예시를 통해 이해해보도록 하겠습니다.
예제5.$f(x) = x^{3} - x$의 2차 미분 $f^{''}(x)$를 구하여라.
$$\begin{align*} f^{''}(x) &= (f^{'})^{'}(x) = \lim_{h \rightarrow 0} \frac{f^{'}(x + h) - f^{'}(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[3(x + h)^{2} - 1\right] - \left[3x^{2} - 1\right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{3x^{2} + 6xh + 3h^{2} - 1 -3x^{2} + 1}{h} \\ &= \lim_{h \rightarrow 0} \left(6x + 3h\right) = 6x\end{align*}$$
연습문제1. 미분의 정의를 이용해서 주어진 함수들의 미분을 계산하라.
(a). $f(x) = \frac{1}{2}x - \frac{1}{3}$
(b). $f(x) = mx + b$
(c). $f(x) = 5x - 9x^{2}$
(d). $f(x) = x^{3} - 3x + 5$
(e). $f(x) = x + \sqrt{x}$
(f). $f(x) = \sqrt{1 + 2x}$
(g). $f(x) = \frac{3 + x}{1 - 3x}$
(h). $f(x) = \frac{4x}{x + 1}$
(i). $f(x) = \frac{1}{\sqrt{x}}$
(j). $f(x) = x^{4}$
(a). $f(x) = \frac{1}{2}x - \frac{1}{3}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ \frac{1}{2}(x + h) - \frac{1}{3} \right] - \left[ \frac{1}{2}x - \frac{1}{3} \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{1}{2}h}{h} = \frac{1}{2} \end{align*}$$
(b). $f(x) = mx + b$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ m(x + h) + b\right] - \left[ mx + b \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{mh}{h} = m \end{align*}$$
(c). $f(x) = 5x - 9x^{2}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ 5(x + h) - 9(x + h)^{2} \right] - \left[ 5x - 9x^{2} \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{5h - 9(2xh + h^{2})}{h} \\ &= \lim_{h \rightarrow 0} \left[ 5 - 9(2x + h) \right] = 5 - 18x \end{align*}$$
(d). $f(x) = x^{3} - 3x + 5$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ (x + h)^{3} - 3(x + h) + 5 \right] - \left[ x^{3} - 3x + 5 \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{3x^{2}h + 3xh^{2} + h^{3} - 3h}{h} \\ &= \lim_{h \rightarrow 0} \left[ 3x^{2} + 3xh + h^{2} - 3 \right] = 3x^{2} - 3 \end{align*}$$
(e). $f(x) = x + \sqrt{x}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ (x + h) + \sqrt{x + h} \right] - \left[ x + \sqrt{x} \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{h + \sqrt{x + h} - \sqrt{x}}{h} \\ &= \lim_{h \rightarrow 0} \left(1 + \frac{\sqrt{x + h} - \sqrt{x}}{h} \right) \\ &= \lim_{h \rightarrow 0} \left[ 1 + \frac{(\sqrt{1 + h} - \sqrt{x})(\sqrt{x + h} + \sqrt{x})}{h (\sqrt{x + h} + \sqrt{x})} \right] \\ &= \lim_{h \rightarrow 0} \left[1 + \frac{1}{\sqrt{x + h} + \sqrt{x}} \right] = 1 + \frac{1}{2\sqrt{x}} \end{align*}$$
(f). $f(x) = \sqrt{1 + 2x}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\sqrt{1 + 2(x + h)} - \sqrt{1 + 2x}}{h} \\ &= \lim_{h \rightarrow 0} \frac{(\sqrt{1 + 2(x + h)} - \sqrt{1 + 2x})(\sqrt{1 + 2(x + h)} + \sqrt{1 + 2x})}{h(\sqrt{1 + 2(x + h)} + \sqrt{1 + 2x})} \\ &= \lim_{h \rightarrow 0} \frac{(1 + 2(x + h)) - (1 + 2x)}{h(\sqrt{1 + 2(x + h)} + \sqrt{1 + 2x})} \\ &= \lim_{h \rightarrow 0} \frac{2}{\sqrt{1 + 2(x + h)} - \sqrt{1 + 2x}} = \frac{1}{\sqrt{1 + 2x}}\end{align*}$$
(g). $f(x) = \frac{3 + x}{1 - 3x}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{3 + x + h}{1 - 3(x + h)} - \frac{3 + x}{1 - 3x}}{h} \\ &= \lim_{x \rightarrow 0} \frac{(3 + x + h)(1 - 3x) - (3 + x)(1 - 3(x + h))}{h(1 - 3(x + h))(1 - 3x)} \\ &= \lim_{h \rightarrow 0} \frac{10}{(1 - 3(x + h))(1 - 3x)} = \frac{10}{(1 - 3x)^{2}}\end{align*}$$
(h). $f(x) = \frac{4x}{x + 1}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{4(x + h)}{(x + h) + 1} - \frac{4x}{x + 1}}{h} \\ &= \lim_{h \rightarrow 0} \frac{4(x + h)(x + 1) - 4x(x + h + 1)}{h(x + h + 1)(x + 1)} \\ &= \lim_{h \rightarrow 0} \frac{4}{(x + h + 1)(x + 1)} = \frac{4}{(x + 1)^{2}} \end{align*}$$
(i). $f(x) = \frac{1}{\sqrt{x}}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{1}{\sqrt{x + h}} - \frac{1}{\sqrt{x}}}{h} \\ &= \lim_{h \rightarrow 0} \frac{\sqrt{x} - \sqrt{x + h}}{h\sqrt{x(x + h)}} \\ &= \lim_{h \rightarrow 0} \frac{(\sqrt{x} - \sqrt{x + h})(\sqrt{x} + \sqrt{x + h})}{h(\sqrt{x(x + h)})(\sqrt{x} + \sqrt{x + h})} \\ &= \lim_{h \rightarrow 0} \frac{-1}{\sqrt{x(x + h)}(\sqrt{x} + \sqrt{x + h})} = -\frac{1}{2x\sqrt{x}} \end{align*}$$
(j). $f(x) = x^{4}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{(x + h)^{4} - x^{4}}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ (x + h)^{2} + x^{2} \right] \left[ (x + h) + x \right] \left[ (x + h) - x \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ (x + h)^{2} + x^{2} \right] (2x + h) h}{h} \\ &= \lim_{h \rightarrow 0} \left[ (x + h)^{2} + x^{2} \right] \left[ 2x + h \right] = 4x^{3} \end{align*}$$
종합연습문제1. $\lim_{x \rightarrow 1} \frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1}$을 계산하라.
$$\begin{align*} \lim_{x \rightarrow 1} \frac{\sqrt[3]{x} - 1}{\sqrt{}x - 1} &= \lim_{x \rightarrow 1} \frac{(\sqrt[3]{x} - 1)(\sqrt{x} + 1)}{(\sqrt{x} - 1)(\sqrt{x} + 1)} \\ &= \lim_{x \rightarrow 1} \frac{(\sqrt[3]{x} - 1)(\sqrt{x} + 1)}{x - 1} \\ &= \lim_{x \rightarrow 1} \frac{(\sqrt[3]{x} - 1)(\sqrt{x} + 1)}{(\sqrt[3]{x} - 1)(\sqrt[3]{x^{2}} + \sqrt[3]{x} + 1)} \\ &= \lim_{x \rightarrow 1} \frac{\sqrt{x} + 1}{\sqrt[3]{x} + \sqrt[3]{x} + 1} = \frac{2}{3} \end{align*}$$
종합연습문제2. $\lim_{x \rightarrow 0} \frac{\sqrt{ax + b} - 2}{x} = 1$을 만족하는 $a$와 $b$를 구하여라.
$$\begin{align*} \lim_{x\ rightarrow 0} \frac{\sqrt{ax + b} - 2}{x} &= \lim_{x \rightarrow 0} \frac{(\sqrt{ax + b} - 2)(\sqrt{ax + b} + 2)}{x(\sqrt{ax + b} + 2)} \\ &= \lim_{x \rightarrow 0} \frac{(ax + b) - 4}{x(\sqrt{ax + b} + 2)} = 1\end{align*}$$
이때, 주어진 극한이 수렴하기 위해서는 분자-분모의 $x$가 소거되어야하기 때문에 $b = 4$이여야한다.
$$\begin{align*} \lim_{x \rightarrow 0} \frac{a}{\sqrt{ax + 4} + 2} = 1\end{align*}$$
마지막으로 극한을 취하면 $\frac{a}{4} = 1$이므로 $a = 4$이다.
종합연습문제3. $\lim_{x \rightarrow 0} \frac{|2x - 1| - |2x + 1|}{x}$를 구하여라.
1). 좌극한 조사 : $x \rightarrow 0^{-}$
$$\begin{align*} \lim_{x \rightarrow 0^{-}} \frac{|2x - 1| - |2x + 1|}{x} &= \lim_{x \rightarrow 0^{-}} \frac{-(2x - 1) - (2x + 1)}{x} \\ &= \lim_{x \rightarrow 0^{-}} \frac{-4x}{x} = -4 \end{align*}$$
2). 우극한 조사 : $x \rightarrow 0^{+}$
$$\begin{align*} \lim_{x \rightarrow 0^{+}} \frac{|2x - 1| - |2x + 1|}{x} &= \lim_{x \rightarrow 0^{+}} \frac{-(2x - 1) - (2x + 1)}{x} \\ &= \lim_{x \rightarrow 0^{+}} \frac{-4x}{x} = -4 \end{align*}$$
좌극한과 우극한 모두 동일한 값으로 수렴하기 때문에 $\lim_{x \rightarrow 0} \frac{|2x - 1| - |2x + 1|}{x} = -4$이다.
종합연습문제4. 아래와 같은 그림이 주여졌을 때 점 $P$가 포물선을 따라 원점으로 향할 때 점 $Q$를 구하여라.
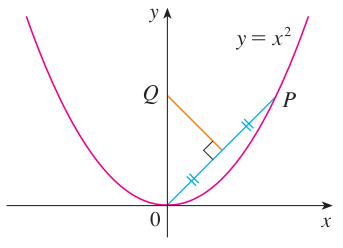
$P(a, a^{2})$이라고 하자. 두 점 $O$와 $P$ 사이의 중점을 $M$이라고 할 때 직선 $QM$의 $y$ 절편을 구해야한다. 먼저, 직선 $OP$의 기울기를 $m_{OP}$이라고 할 때 $m_{OP} = \frac{a^{2} - 0}{a - 0} = a$이다.
이때, 직선 $QM$은 직선과 수직이므로 직선 $QM$의 기울기는 $m_{QM} = -\frac{1}{a}$이다. 따라서, 직선의 방정식을 $y = -\frac{1}{a}x + b$라고 둘 수 있다. 여기서 직선 $QM$은 중점 $M(\frac{a}{2}, \frac{a^{2}}{2})$를 지나므로 이를 대입하여 $b$를 구할 수 있다.
$$\frac{a^{2}}{2} = -\frac{1}{a} \cdot \frac{a}{2} + b \Rightarrow b = \frac{a^{2}}{2} + 1$$
따라서, 점 $Q$는 직선 $QM$의 $y$ 절편이므로 $(0, \frac{a^{2}}{2} + 1)$이다. 마지막으로 점 $P$는 포물선을 따라 원점으로 향하므로 $a \rightarrow 0$로의 극한을 점 $Q$에 대해서 취해주면 된다.
$$\lim_{a \rightarrow 0} \left(\frac{a^{2}}{2} + 1\right) = 1$$
따라서, 점 $Q$는 점 $P$가 포물선을 따라 원점으로 다가가면 $(0, 1)$로 수렴한다.
종합연습문제5. $\lim_{x \rightarrow a} \left[ f(x) + g(x) \right] = 2$ 그리고 $\lim_{x \rightarrow a} \left[ f(x) - g(x) \right] = 1$라고 할 때 $\lim_{x \rightarrow a} \left[ f(x)g(x) \right]$를 구하여라.
미적분학 - 극한 법칙을 이용한 극한 계산하기의 극한 성질을 이용해서 문제를 풀 수 있다. $\lim_{x \rightarrow a} \left[ f(x) + g(x) \right] = 2$이므로 $\lim_{x \rightarrow a} \left[ f(x) + g(x) \right]^{2} = 4$이다.
이때, $(a + b)^{2} = (a - b)^{2} + 4ab$임을 이용하면 아래와 같이 극한을 쓸 수 있다.
$$\begin{align*} \lim_{x \rightarrow a} \left[ f(x) + g(x) \right]^{2} = \lim_{x \rightarrow a} \left[ (f(x) - g(x)) + 4f(x)g(x) \right] \\ &= 1 + 4\lim_{x \rightarrow a} \left[ f(x)g(x) \right] = 4\end{align*}$$
이 식을 정리하면 $\lim_{x \rightarrow a} \left[ f(x)g(x) \right] = \frac{3}{4}$임을 알 수 있다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.08.22 : 전체적인 스타일 수정
22.08.22 : 연습문제1 추가
22.08.29 : 종합연습문제1-5 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 곱의 미분과 몫 미분 (0) | 2021.10.29 |
|---|---|
| 미적분학 - 다항함수와 지수함수의 미분 (0) | 2021.10.27 |
| 미적분학 - 미분 개요 (0) | 2021.10.22 |
| 미적분학 - 무한대 극한 (0) | 2021.09.07 |
| 미적분학 - 연속함수 (1) | 2021.08.29 |
안녕하세요. 지난 포스팅의 미적분학 - 미분 개요에서는 접선(Tangent)와 미분(Derivative)에 대해서 알아보았습니다. 오늘은 지난 번에 알아본 미분을 임의의 점으로 확장해보도록 하겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
정의1. 함수 미분(Function Derivative)
함수 $f$의 임의의 점 $x \in \text{dom}(f)$에서의 함수 미분(Function Derivative)은 극한이 존재한다면 아래와 같이 정의된다.
$$f^{'}(x) = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h}$$
이때, 미분의 기호는 다양하며 아래의 기호들 모두 동일한 의미이다.
$$f^{'}(x) = y^{'} = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx}f(x) = Df(x) = D_{x}f(x)$$
설명
저희는 지난 포스팅에서 미분이랑 함수의 각 점에서 접선의 기울기와 같다는 것을 알게 되었습니다. 다만 차이점은 오늘 포스팅에서는 임의의 점에서의 미분을 구하기 위해 이를 함수와 같이 표현하는 것입니다.(지난 포스팅에서는 하나의 점에서의 기울기를 구하였죠?) 간단한 예제들을 통해 함수 미분의 정의를 이용하여 구하는 방법에 대해서 알아보도록 하겠습니다.
예제1. 함수 $f(x) = x^{3} - x$의 미분 $f^{'}(x)$을 구하여라.
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[(x + h)^{3} - (x + h)\right] - \left(x^{3} - x\right)}{h} \\ &= \lim_{h \rightarrow 0} \frac{x^{3} + 3x^{2}h + 3xh^{2} + h^{3} - x^{3} - x}{h} \\ &= \lim_{h \rightarrow 0} \frac{3x^{2}h + 3xh^{2} + h^{3} - h}{h} \\ &= \lim_{h \rightarrow 0} \left(3x^{2} + 3xh + h^{2} - 1\right) = 3x^{2} - 1\end{align*}$$
예제2. 함수 $f(x) = \sqrt{x}$의 미분 $f^{'}(x)$을 구하여라.
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\sqrt{x + h} - \sqrt{x}}{h} \\ &= \lim_{h \rightarrow 0} \left(\frac{\sqrt{x + h} - \sqrt{x}}{h} \cdot \frac{\sqrt{x+ h} + \sqrt{x}}{\sqrt{x + h} + \sqrt{x}}\right) \\ &= \lim_{h \rightarrow 0} \frac{(x + h) - h}{h(\sqrt{x + h} + \sqrt{x})} \\ &= \lim_{h \rightarrow 0} \frac{1}{\sqrt{x + h} + \sqrt{x}} \\ &= \frac{1}{\sqrt{x} + \sqrt{x}} = \frac{1}{2\sqrt{x}}\end{align*}$$
예제3.함수 $f(x) = \frac{1 - x}{2 + x}$의 미분 $f^{'}(x)$을 구하여라.
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{1 - x - h}{2 + x + h} - \frac{1 - x}{2 + x}}{h} \\ &= \lim_{h \rightarrow 0} \frac{(1 - x - h)(2 + x) - (1 - x)(2 + x + h)}{h(2 + x + h)(2 + x)} \\ &= \lim_{h \rightarrow 0} \frac{(2 - x - 2h - x^{2} - xh) - (2 - x + h - x^{2} - xh)}{h} \\ &= \lim_{h \rightarrow 0} \frac{-3h}{h(2 + x + h)(2 + x)} \\ &= \lim_{h \rightarrow 0} \frac{-3}{(2 + x + h)(2 + x)} = -\frac{3}{(2 + x)^{2}}\end{align*}$$
정의2. 미분가능성(Differentiability)
함수 $f$는 $f^{'}(a)$가 존재하면 $x = a$에서 미분가능(Differentiable)하다. 만약, 함수 $f$가 열린 구간 $ I = (a, b), (a, \infty), (-\infty, b), (-\infty, \infty)$의 모든 점 $x \in I$에서 미분가능하면 구간 $I$에서 미분가능하다.
설명
기본적으로 미분의 정의를 고려해본다면 당연하겠지만 미분이 가능하기 위해서는 해당 점에서 극한이 존재해야합니다. 극한의 존재성에 대한 내용은 제거 해당 포스팅에 정리해놓았으니 보고 오시는 것을 추천드립니다. 요약만 해드리면 아래와 같습니다.
미적분학 - 함수의 극한
안녕하세요. 지난 포스팅의 미적분학 - 접선에서는 어떤 점에서 곡선의 접선을 찾는 근사적인 방법에 대해서 알아보았습니다. 오늘은 이를 명확하게 정의하기 위해서 함수의 극한에 대해서 알
everyday-image-processing.tistory.com
정의2-1. 극한의 존재성
함수 $f$가 $x = a$에서 극한이 존재하기 위해서는 좌극한과 우극한이 동일한 값으로 수렴해야한다.
$$\lim_{x \rightarrow a} f(x) = L \text{ if and only if } \lim_{x \rightarrow a^{-}} f(x) = \lim_{x \rightarrow a^{+}} f(x) = L$$
설명
따라서 저희는 간단한 예시에서 위와 같은 존재성에 대한 정의를 활용하여 실제로 미분이 가능한지 불가능한지 판별해보도록 하겠습니다.
예제4. $f(x) = |x|$는 $x = a$에서 미분가능한가?
불가능하다.
1). $x > 0$이라고 했을 때, $f(x) = |x| = x$이다. 그리고 $x + h > 0$를 만족하는 아주 작은 $h$를 고려하면 $|x + h| = x + h$이다. 따라서, $x > 0$일 때,
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{|x + h| - |x|}{h} \\ &= \lim_{h \rightarrow 0} \frac{x + h - x}{h} = \lim_{h \rightarrow 0} \frac{h}{h} = 1 \end{align*}$$
2). $x < 0$이라고 했을 때, $f(x) = |x| = -x$이다. 그리고 $x + h < 0$를 만족하는 아주 작은 $h$를 고려하면 $|x + h| = -x - h$이다. 따라서, $x < 0$일 때,
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{|x + h| - |x|}{h} \\ &= \lim_{h \rightarrow 0} \frac{-x - h + x}{h} = \lim_{h \rightarrow 0} \frac{-h}{h} = -1 \end{align*}$$
$f(x) = |x|$는 $x = 0$에서 $\lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h}$의 극한값이 존재하지 않기 때문에 $f(x)$는 $x = 0$에서 미분불가능하다.
3.정리
함수 $f$가 $x = a$에서 미분가능하면, 함수 $f$는 $x = a$에서 연속이다.
설명
이 정리의 증명을 해보도록 하겠습니다. 먼저, 지난 포스팅의 미적분학 - 연속함수에서 보았던 연속함수의 정의를 상기해보도록 하겠습니다. 함수 $f$가 $x = a$에서 연속이기 위해서는 $\lim_{x \rightarrow a} f(x) = f(a)$를 만족해야하기 때문에 $f(x) - f(a)$가 $x \rightarrow a$로의 극한을 취할 때 0으로 수렴하는 것을 보여야하죠.
그리고 함수 $f$가 $x = a$에서 미분가능하기 때문에 함수 미분의 정의에 따라서 아래의 극한이 존재하게 됩니다.
$$f^{'}(a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}$$
한편, $f(x) - f(a) = \frac{f(x) - f(a)}{x - a} \cdot (x - a)$이기 때문에 다시 한번 식을 정리하여 쓸 수 있습니다.
$$\begin{align*} \lim_{x \rightarrow a} \left[f(x) - f(a)\right] &= \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a} \cdot (x - a) \\ &= \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a} \cdot \lim_{x \rightarrow a} (x - a) \\ &= f^{'}(a) \cdot 0 = 0 \end{align*}$$
하지만, 저희는 최종적으로 $\lim_{x \rightarrow a} f(x) = f(a)$임을 증명해야하기 때문에 아래와 같은 식조작을 한번 더 해주면 됩니다.
$$\begin{align*} \lim_{x \rightarrow a} f(x) &= \lim_{x \rightarrow a} \left[f(a) + (f(x) -f(a))\right] \\ &= \lim_{x \rightarrow a} f(a) + \lim_{x \rightarrow a} \left[f(x) - f(a)\right] \\ &= f(a) + 0 = f(a) \end{align*}$$
따라서, $\lim_{x \rightarrow a} f(x) = f(a)$을 만족하기 때문에 함수 $f$는 $x = a$에서 연속이다.
정의4. 고계 미분(Higher Derivative)
함수 $f$가 미분가능할 때, 그의 도함수 $f^{'}$의 2차 미분 $f^{''}$은 아래와 같이 정의된다.
$$\frac{d}{dx}\left(\frac{dy}{dx}\right) = \frac{d^{2}y}{dx^{2}}$$
설명
고계 미분은 위에서 설명한 2차 미분뿐만 아니라 3차, 4차, 5차 등 더 높은 차수의 미분까지도 계산될 수 있습니다. 그리고 그 과정은 전부 1차 미분과 동일하게 이어지기 때문에 간단한 예시를 통해 이해해보도록 하겠습니다.
예제5.$f(x) = x^{3} - x$의 2차 미분 $f^{''}(x)$를 구하여라.
$$\begin{align*} f^{''}(x) &= (f^{'})^{'}(x) = \lim_{h \rightarrow 0} \frac{f^{'}(x + h) - f^{'}(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[3(x + h)^{2} - 1\right] - \left[3x^{2} - 1\right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{3x^{2} + 6xh + 3h^{2} - 1 -3x^{2} + 1}{h} \\ &= \lim_{h \rightarrow 0} \left(6x + 3h\right) = 6x\end{align*}$$
연습문제1. 미분의 정의를 이용해서 주어진 함수들의 미분을 계산하라.
(a). $f(x) = \frac{1}{2}x - \frac{1}{3}$
(b). $f(x) = mx + b$
(c). $f(x) = 5x - 9x^{2}$
(d). $f(x) = x^{3} - 3x + 5$
(e). $f(x) = x + \sqrt{x}$
(f). $f(x) = \sqrt{1 + 2x}$
(g). $f(x) = \frac{3 + x}{1 - 3x}$
(h). $f(x) = \frac{4x}{x + 1}$
(i). $f(x) = \frac{1}{\sqrt{x}}$
(j). $f(x) = x^{4}$
(a). $f(x) = \frac{1}{2}x - \frac{1}{3}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ \frac{1}{2}(x + h) - \frac{1}{3} \right] - \left[ \frac{1}{2}x - \frac{1}{3} \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{1}{2}h}{h} = \frac{1}{2} \end{align*}$$
(b). $f(x) = mx + b$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ m(x + h) + b\right] - \left[ mx + b \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{mh}{h} = m \end{align*}$$
(c). $f(x) = 5x - 9x^{2}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ 5(x + h) - 9(x + h)^{2} \right] - \left[ 5x - 9x^{2} \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{5h - 9(2xh + h^{2})}{h} \\ &= \lim_{h \rightarrow 0} \left[ 5 - 9(2x + h) \right] = 5 - 18x \end{align*}$$
(d). $f(x) = x^{3} - 3x + 5$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ (x + h)^{3} - 3(x + h) + 5 \right] - \left[ x^{3} - 3x + 5 \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{3x^{2}h + 3xh^{2} + h^{3} - 3h}{h} \\ &= \lim_{h \rightarrow 0} \left[ 3x^{2} + 3xh + h^{2} - 3 \right] = 3x^{2} - 3 \end{align*}$$
(e). $f(x) = x + \sqrt{x}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ (x + h) + \sqrt{x + h} \right] - \left[ x + \sqrt{x} \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{h + \sqrt{x + h} - \sqrt{x}}{h} \\ &= \lim_{h \rightarrow 0} \left(1 + \frac{\sqrt{x + h} - \sqrt{x}}{h} \right) \\ &= \lim_{h \rightarrow 0} \left[ 1 + \frac{(\sqrt{1 + h} - \sqrt{x})(\sqrt{x + h} + \sqrt{x})}{h (\sqrt{x + h} + \sqrt{x})} \right] \\ &= \lim_{h \rightarrow 0} \left[1 + \frac{1}{\sqrt{x + h} + \sqrt{x}} \right] = 1 + \frac{1}{2\sqrt{x}} \end{align*}$$
(f). $f(x) = \sqrt{1 + 2x}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\sqrt{1 + 2(x + h)} - \sqrt{1 + 2x}}{h} \\ &= \lim_{h \rightarrow 0} \frac{(\sqrt{1 + 2(x + h)} - \sqrt{1 + 2x})(\sqrt{1 + 2(x + h)} + \sqrt{1 + 2x})}{h(\sqrt{1 + 2(x + h)} + \sqrt{1 + 2x})} \\ &= \lim_{h \rightarrow 0} \frac{(1 + 2(x + h)) - (1 + 2x)}{h(\sqrt{1 + 2(x + h)} + \sqrt{1 + 2x})} \\ &= \lim_{h \rightarrow 0} \frac{2}{\sqrt{1 + 2(x + h)} - \sqrt{1 + 2x}} = \frac{1}{\sqrt{1 + 2x}}\end{align*}$$
(g). $f(x) = \frac{3 + x}{1 - 3x}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{3 + x + h}{1 - 3(x + h)} - \frac{3 + x}{1 - 3x}}{h} \\ &= \lim_{x \rightarrow 0} \frac{(3 + x + h)(1 - 3x) - (3 + x)(1 - 3(x + h))}{h(1 - 3(x + h))(1 - 3x)} \\ &= \lim_{h \rightarrow 0} \frac{10}{(1 - 3(x + h))(1 - 3x)} = \frac{10}{(1 - 3x)^{2}}\end{align*}$$
(h). $f(x) = \frac{4x}{x + 1}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{4(x + h)}{(x + h) + 1} - \frac{4x}{x + 1}}{h} \\ &= \lim_{h \rightarrow 0} \frac{4(x + h)(x + 1) - 4x(x + h + 1)}{h(x + h + 1)(x + 1)} \\ &= \lim_{h \rightarrow 0} \frac{4}{(x + h + 1)(x + 1)} = \frac{4}{(x + 1)^{2}} \end{align*}$$
(i). $f(x) = \frac{1}{\sqrt{x}}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{\frac{1}{\sqrt{x + h}} - \frac{1}{\sqrt{x}}}{h} \\ &= \lim_{h \rightarrow 0} \frac{\sqrt{x} - \sqrt{x + h}}{h\sqrt{x(x + h)}} \\ &= \lim_{h \rightarrow 0} \frac{(\sqrt{x} - \sqrt{x + h})(\sqrt{x} + \sqrt{x + h})}{h(\sqrt{x(x + h)})(\sqrt{x} + \sqrt{x + h})} \\ &= \lim_{h \rightarrow 0} \frac{-1}{\sqrt{x(x + h)}(\sqrt{x} + \sqrt{x + h})} = -\frac{1}{2x\sqrt{x}} \end{align*}$$
(j). $f(x) = x^{4}$
$$\begin{align*} f^{'}(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ &= \lim_{h \rightarrow 0} \frac{(x + h)^{4} - x^{4}}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ (x + h)^{2} + x^{2} \right] \left[ (x + h) + x \right] \left[ (x + h) - x \right]}{h} \\ &= \lim_{h \rightarrow 0} \frac{\left[ (x + h)^{2} + x^{2} \right] (2x + h) h}{h} \\ &= \lim_{h \rightarrow 0} \left[ (x + h)^{2} + x^{2} \right] \left[ 2x + h \right] = 4x^{3} \end{align*}$$
종합연습문제1. $\lim_{x \rightarrow 1} \frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1}$을 계산하라.
$$\begin{align*} \lim_{x \rightarrow 1} \frac{\sqrt[3]{x} - 1}{\sqrt{}x - 1} &= \lim_{x \rightarrow 1} \frac{(\sqrt[3]{x} - 1)(\sqrt{x} + 1)}{(\sqrt{x} - 1)(\sqrt{x} + 1)} \\ &= \lim_{x \rightarrow 1} \frac{(\sqrt[3]{x} - 1)(\sqrt{x} + 1)}{x - 1} \\ &= \lim_{x \rightarrow 1} \frac{(\sqrt[3]{x} - 1)(\sqrt{x} + 1)}{(\sqrt[3]{x} - 1)(\sqrt[3]{x^{2}} + \sqrt[3]{x} + 1)} \\ &= \lim_{x \rightarrow 1} \frac{\sqrt{x} + 1}{\sqrt[3]{x} + \sqrt[3]{x} + 1} = \frac{2}{3} \end{align*}$$
종합연습문제2. $\lim_{x \rightarrow 0} \frac{\sqrt{ax + b} - 2}{x} = 1$을 만족하는 $a$와 $b$를 구하여라.
$$\begin{align*} \lim_{x\ rightarrow 0} \frac{\sqrt{ax + b} - 2}{x} &= \lim_{x \rightarrow 0} \frac{(\sqrt{ax + b} - 2)(\sqrt{ax + b} + 2)}{x(\sqrt{ax + b} + 2)} \\ &= \lim_{x \rightarrow 0} \frac{(ax + b) - 4}{x(\sqrt{ax + b} + 2)} = 1\end{align*}$$
이때, 주어진 극한이 수렴하기 위해서는 분자-분모의 $x$가 소거되어야하기 때문에 $b = 4$이여야한다.
$$\begin{align*} \lim_{x \rightarrow 0} \frac{a}{\sqrt{ax + 4} + 2} = 1\end{align*}$$
마지막으로 극한을 취하면 $\frac{a}{4} = 1$이므로 $a = 4$이다.
종합연습문제3. $\lim_{x \rightarrow 0} \frac{|2x - 1| - |2x + 1|}{x}$를 구하여라.
1). 좌극한 조사 : $x \rightarrow 0^{-}$
$$\begin{align*} \lim_{x \rightarrow 0^{-}} \frac{|2x - 1| - |2x + 1|}{x} &= \lim_{x \rightarrow 0^{-}} \frac{-(2x - 1) - (2x + 1)}{x} \\ &= \lim_{x \rightarrow 0^{-}} \frac{-4x}{x} = -4 \end{align*}$$
2). 우극한 조사 : $x \rightarrow 0^{+}$
$$\begin{align*} \lim_{x \rightarrow 0^{+}} \frac{|2x - 1| - |2x + 1|}{x} &= \lim_{x \rightarrow 0^{+}} \frac{-(2x - 1) - (2x + 1)}{x} \\ &= \lim_{x \rightarrow 0^{+}} \frac{-4x}{x} = -4 \end{align*}$$
좌극한과 우극한 모두 동일한 값으로 수렴하기 때문에 $\lim_{x \rightarrow 0} \frac{|2x - 1| - |2x + 1|}{x} = -4$이다.
종합연습문제4. 아래와 같은 그림이 주여졌을 때 점 $P$가 포물선을 따라 원점으로 향할 때 점 $Q$를 구하여라.

$P(a, a^{2})$이라고 하자. 두 점 $O$와 $P$ 사이의 중점을 $M$이라고 할 때 직선 $QM$의 $y$ 절편을 구해야한다. 먼저, 직선 $OP$의 기울기를 $m_{OP}$이라고 할 때 $m_{OP} = \frac{a^{2} - 0}{a - 0} = a$이다.
이때, 직선 $QM$은 직선과 수직이므로 직선 $QM$의 기울기는 $m_{QM} = -\frac{1}{a}$이다. 따라서, 직선의 방정식을 $y = -\frac{1}{a}x + b$라고 둘 수 있다. 여기서 직선 $QM$은 중점 $M(\frac{a}{2}, \frac{a^{2}}{2})$를 지나므로 이를 대입하여 $b$를 구할 수 있다.
$$\frac{a^{2}}{2} = -\frac{1}{a} \cdot \frac{a}{2} + b \Rightarrow b = \frac{a^{2}}{2} + 1$$
따라서, 점 $Q$는 직선 $QM$의 $y$ 절편이므로 $(0, \frac{a^{2}}{2} + 1)$이다. 마지막으로 점 $P$는 포물선을 따라 원점으로 향하므로 $a \rightarrow 0$로의 극한을 점 $Q$에 대해서 취해주면 된다.
$$\lim_{a \rightarrow 0} \left(\frac{a^{2}}{2} + 1\right) = 1$$
따라서, 점 $Q$는 점 $P$가 포물선을 따라 원점으로 다가가면 $(0, 1)$로 수렴한다.
종합연습문제5. $\lim_{x \rightarrow a} \left[ f(x) + g(x) \right] = 2$ 그리고 $\lim_{x \rightarrow a} \left[ f(x) - g(x) \right] = 1$라고 할 때 $\lim_{x \rightarrow a} \left[ f(x)g(x) \right]$를 구하여라.
미적분학 - 극한 법칙을 이용한 극한 계산하기의 극한 성질을 이용해서 문제를 풀 수 있다. $\lim_{x \rightarrow a} \left[ f(x) + g(x) \right] = 2$이므로 $\lim_{x \rightarrow a} \left[ f(x) + g(x) \right]^{2} = 4$이다.
이때, $(a + b)^{2} = (a - b)^{2} + 4ab$임을 이용하면 아래와 같이 극한을 쓸 수 있다.
$$\begin{align*} \lim_{x \rightarrow a} \left[ f(x) + g(x) \right]^{2} = \lim_{x \rightarrow a} \left[ (f(x) - g(x)) + 4f(x)g(x) \right] \\ &= 1 + 4\lim_{x \rightarrow a} \left[ f(x)g(x) \right] = 4\end{align*}$$
이 식을 정리하면 $\lim_{x \rightarrow a} \left[ f(x)g(x) \right] = \frac{3}{4}$임을 알 수 있다.
참고자료 및 그림출처
Calculus(J. Stewart)
변경사항
22.08.22 : 전체적인 스타일 수정
22.08.22 : 연습문제1 추가
22.08.29 : 종합연습문제1-5 추가
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 곱의 미분과 몫 미분 (0) | 2021.10.29 |
|---|---|
| 미적분학 - 다항함수와 지수함수의 미분 (0) | 2021.10.27 |
| 미적분학 - 미분 개요 (0) | 2021.10.22 |
| 미적분학 - 무한대 극한 (0) | 2021.09.07 |
| 미적분학 - 연속함수 (1) | 2021.08.29 |
