안녕하세요. 지난 포스팅의 [IC2D] Evolving Attention with Residual Connections (ICML2021)에서는 기존 CNN이나 Transformer가 수행하던 단일 계층에서의 어텐션이 아닌 서로 간의 residual connection을 도입하여 보다 추출되는 어텐션 맵을 정교하게 뽑아낼 수 있는 모듈인 Evolving Attention을 제안하였습니다. 최근 인공지능의 효율성을 강조한 모델들이 많이 나오게 되었는데 오늘 역시도 기존의 효율적인 모델의 대표격인 CondenseNet의 확장된 버전인 CondenseNet V2에 대해서 알아보도록 하겠습니다.
Background
지금까지 저희가 보아왔던 다양한 CNN 또는 Transformer 기반들은 충분한 computational resoure가 있다라고 가정한 상태에서 모델을 설계했기 때문에 실질적으로 real-time에 동작하지 않는 경우가 굉장히 많았습니다. 특히, DenseNet (CVRP2017)에서는 특정 계층의 특징 맵을 얻기 위해서는 ResNet (CVPR2016)과는 달리 모든 계층들의 특징 맵을 다시 불러와야합니다. 이는 굉장한 computational overhead가 들어갈 수 밖에 없겠죠. 이러한 모델의 복잡성은 당시의 유행 중 하나였던 "더 깊은 모델을 설계"하는 것에 방해가 되는 요인이 되었습니다.
따라서, 이러한 복잡성을 줄이기 위해 몇 가지 트릭이 존재합니다. 가장 대표적으로 필요없는 특징 맵이나 가중치의 연결을 제거하는 pruning, 부동소수점 32비트로 사용되는 딥 러닝 모델을 16비트 또는 integer까지 줄이는 quantization, 그리고 모델 자체의 효율성 증대를 위해 제안된 MobileNet V1 (arxiv2017), MobileNet V2 (CVPR2018), MobileNet V3 (ICCV2019), ShuffleNet V1 (CVPR2018), ShuffleNet V2 (ECCV2018), CondenseNet V1 (CVPR2018) 등이 있었습니다.
특히, 오늘은 핵심 타겟 논문인 CondenseNet V1의 경우 DenseNet의 효율적인 모델 중 하나로써 feature aggregation 시 모든 특징 맵에 대해 합성곱을 수행하는 것이 아니라 어떤 특징 맵이 학습에 의미있는 결과를 내는 지 계산하는 Learned Group Convolution (LGC)를 제안하여 sparsification을 수행하는 모델입니다. 그리고 ShuffleNet V2의 경우 너무 멀리있는 특징 맵은 현재 특징 맵과 너무 관련이 없는 것으로 판단하여 pruning을 수행하게 됩니다. 하지만, 초기 특징맵도 어쩌면 모델의 일반화 능력 향상에 중요한 정보를 가지고 있을 수도 있고, 이를 적절히 활용하면 모델의 효율성 향상에 도움이 될 수 있을지도 모릅니다.
따라서 본 논문에서는 CondenseNet V1과 ShuffleNet V2를 보다 발전시켜 Sparse Feature Reactivation (SFR) 모듈을 도입하고 이를 기반으로 CondeseNet V2를 제안하게 되었습니다.
Method
1) Feature Reuse Mechanism
먼저 DenseNet에서 사용되는 Feature Reuse Mechanism을 수식으로 풀어서 보면 다음과 같습니다. 여기서 $l$번째 계층을 중심으로 보도록 하겠습니다.
$$\mathbf{x}_{l} = H_{l} ([\mathbf{x}_{0}, \mathbf{x}_{1}, \dots, \mathbf{x}_{l - 1}])$$
이때, $H_{l} (\cdot)$은 $l$번째 계층의 Composition Function으로 정의됩니다. 위와 같이 DenseNet에서는 이전 계층들의 모든 특징 맵을 가져와서 하나로 aggregation해주는 composition function $H_{l} (\cdot)$을 통해 $l$번째 계층의 입력을 만드는 것이죠.
CondenseNet V1에서는 LGC를 $H_{l} (\cdot)$에 임베딩시켜 group convolution을 기반으로 중요하지 않은 계층 간 연결을 제거해버리는 방식으로 효율성을 증가시켰죠. ShuffleNet V2에서 $H_{l} (\cdot)$을 feature dropping function으로 정의하여 너무 멀리떨어진 특징 맵은 가져오지 않는 방식으로 학습을 진행하였습니다.
하지만 DenseNet과 같이 일반적인 deterministic model은 특징 맵을 한번 만들게 되면 항상 동일한 특징 맵을 만든다는 성질이 있습니다. 이는 더 깊은 계층에서 feature reuse mechanism을 도입할 때 초기에 얕은 계층에서 나오는 특징 맵들이 한번 안쓰이기 시작하면 계속 안쓰이게 된다는 것을 의미합니다. 이와 같은 Static Design으로 인해 초기 계층의 정보를 적절하게 활용할 수 없는 것이죠. 따라서, 본 논문에서는 이러한 문제점을 지적하며 이전 계층들의 특징 맵을 가져올 때 어떤 특징 맵을 재사용해야할 지에 대한 알고리즘인 Sparse Feature Reactivation (SFR) 모듈을 제안하게 되었습니다.
2) Reactivating Obsolete Features
$l$번째 계층에 대해서 feature reactivation module $G_{l} (\cdot)$을 도입하면 다음과 같이 Feature Reuse Mechanism 부분을 바꿀 수 있습니다.
$$\begin{cases} &\mathbf{x}^{\text{in}}_{l} = [ \mathbf{x}_{0}, \mathbf{x}_{1}, \dots, \mathbf{x}_{l - 1} ] \\ &\mathbf{x}_{l} = H_{l} (\mathbf{x}^{\text{in}}_{l}) \\ &\mathbf{y}_{l} = G_{l} (\mathbf{x}_{l}) \\ &\mathbf{x}^{\text{out}}_{l} = U(\mathbf{x}^{\text{in}}_{l}, \mathbf{y}_{l})\\ &[ \mathbf{x}_{0}, \mathbf{x}_{1}, \dots, \mathbf{x}_{l - 1} ] = \mathbf{x}^{\text{out}}_{l} \end{cases}$$
해당 수식에서 제일 중요한 부분이 $G_{l} (\cdot)$과 $U (\cdot, \cdot)$입니다. $G_{l} (\cdot)$은 위에서 언급드린 것처럼 feature reactivation module을 의미하고 $U (\cdot, \cdot)$은 feature reactivation operation으로 더하기 또는 어텐션 모듈로 정의될 수 있습니다. 다만 본 논문에서는 효율성을 위해 단순 원소별 더하기 (elementary-wise summation)로 정의하였습니다.
3) Sparse Feature Reactivation (SFR)

SFR 모듈의 제안 배경 자체가 모든 feature map들이 reactivation될 필요없다는 것으로 시작하기 때문에 pruning 알고리즘기반으로 설계를 합니다. 그림 2는 이러한 SFR 모듈의 전체적인 구조를 보여주고 있습니다. 본 논문에서는 $G_{l} (\cdot)$을 $1\times 1$의 Convolution + Batch Normalization + ReLU 연산으로 정의합니다. 여기서 $G_{l} (\cdot)$의 필터 크기가 어차피 $1 \times 1$이기 때문에 가중치의 크기를 2차원의 형태로 $(O, I)$와 같이 표현할 수 있습니다. 이때, $O$와 $I$는 각각 출력 및 입력 특징 맵의 채널 개수로 정의됩니다.
CondenseNet V1에서 했던 것과 마찬가지로 SFR 역시 $G_{l} (\cdot)$을 group convolution으로 정의합니다. 총 $G$개의 그룹으로 나눈다고 가정하면 각 그룹에 대한 가중치 $\mathbf{F}^{1}, \mathbf{F}^{2}, \dots, \mathbf{F}^{G}$의 크기는 $(O, I / G)$로 정의됩니다. 이제 마지막으로 reactivation connection의 sparsification을 증가시키기 위해 Sparse Factor $S$를 도입하여 $(O / S, I / G)$로 형상을 바꾸어줍니다. 즉, 출력 특징 맵이 $S$에 의해 $O$개의 특징 맵 중 $\frac{O}{S}$개의 중요한 특징 맵만 선택됩니다. 전체 학습 역시 CondenseNet V1과 마찬가지로 $S - 1$개의 Sparsification Stage와 1개의 Optimization Stage로 구성되어 있습니다.
이는 기본적으로 각 계층의 $G_{l} (\cdot)$에서는 $G$개의 이진 마스크에 의해 연결 패턴이 결정됩니다. 따라서, $g = 1, \dots, G$에 대해서 $\mathbf{M}^{g} \in \{ 0, 1 \}^{O \times \frac{I}{G}}$를 학습하여 필요하지 않은 그룹 간의 연결을 삭제하게 되는 것이죠. 그러므로 $\mathbf{M}^{g} \odot \mathbf{F}^{g}$를 수행하면 간단하게 얻을 수 있습니다. 이때, 학습 초기에는 $\mathbf{M}^{g}$는 1로 채워진 행렬로 초기화된다는 점에 유의하시면 됩니다. 그리고 어떤 그룹이 필요없는 지에 대한 기준은 해당 그룹의 L1-norm $\sum_{j = 1}^{I / G} | \mathbf{F}^{g}_{i, j} |$를 이용하여 결정합니다.

이제 모든 학습이 종료되고 시험 단계에서는 standard group convolution와 index layer를 도입하면 쉽게 구현할 수 있습니다. 이는 CondenseNet V1과 동일합니다.
CondenseNet V2 Architecture
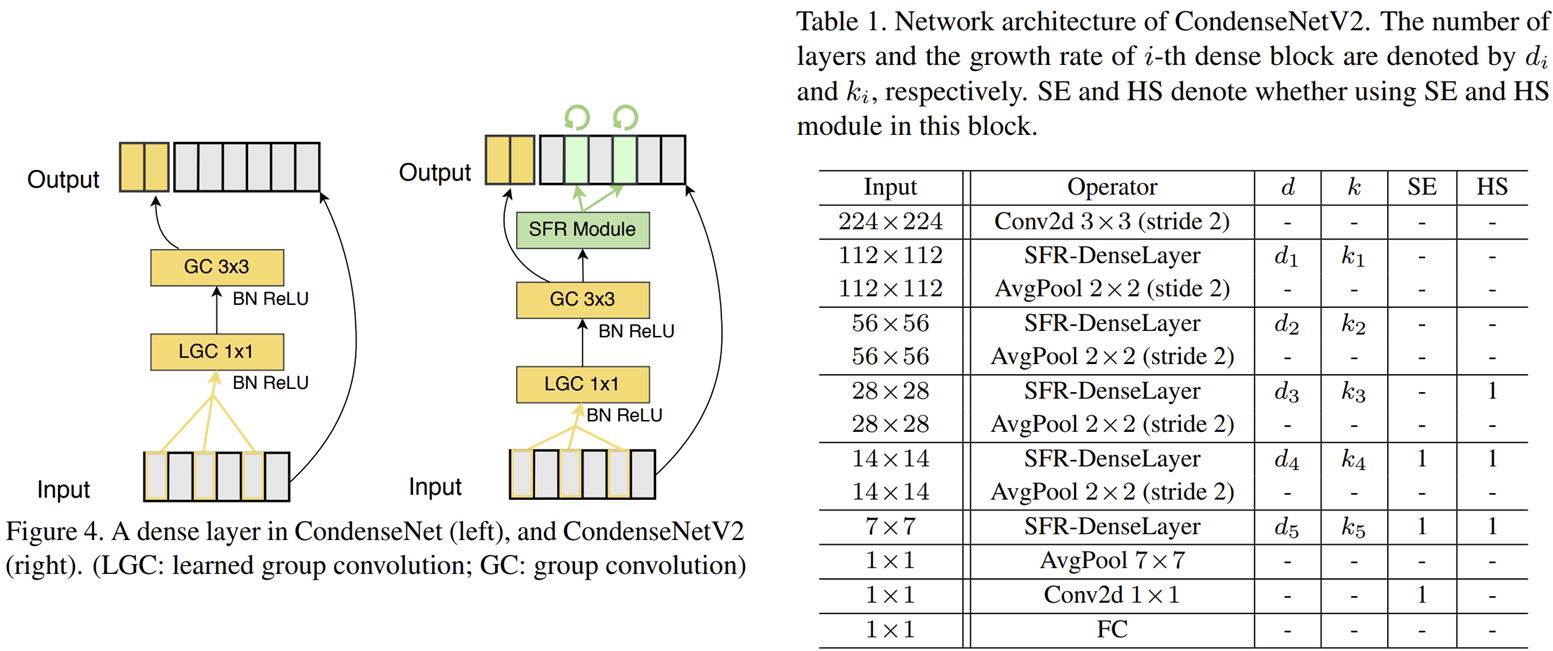
위에서 그림 4은 CondenseNet V1과 CondenseNet V2의 차이점을 블록 다이어그램으로 보여주고 있습니다. 보시면 LGC, GC를 사용하는 것은 동일하지만 CondenseNet V2에서는 SFR 모듈이 추가되어 feature reactivation을 수행하게 됩니다. 표 1은 CondenseNet V2의 상세 파라미터를 보여주고 있습니다. SE Block (CVPR2018)과 Hard-Swish Nonlinearity를 도입한 것을 볼 수 있습니다.

그림 5는 SFR 모듈이 다양하게 활용될 수 있다는 점을 보이기 위해 ShuffleNet V2에 SFR 모듈을 적용한 그림을 볼 수 있습니다. 이를 앞으로 SFR-ShuffleNet V2라고 부르도록 하겠습니다.
Experiment
1) ImageNet Classification
- Dataset
- ImageNet-1K: 1.28 million training images & 50K validation images with 1,000 classes
- Data Augmentation : -
- Optimization: Stochastic Gradient Descent
- momentum: -
- weight decay: -
- initial learning rate of 0.4 , the cosine learning rate
- batch size: 1024
- epochs: -
- GPU 언급 X

