안녕하세요. 지난 포스팅의 [IC2D] ECA-net: Efficient Channel Attention for Deep Convolutional Neural Networks (CVPR2020)에서는 대표적인 어텐션 모듈이였던 SE Block을 보다 깊게 분석하여 spatial relationship을 최대한 보존하면서 어텐션 맵을 얻을 수 있는 ECA Block에 대해서 소개시켜드렸습니다. 오늘도 역시 어텐션과 관련된 논문으로 아직 소개는 하지 않았지만 Attention Augmented ResNet의 발전된 모델이라고 보면 될 거 같습니다. 즉, Self-Attention을 기존의 CNN 모델에 결합한 형태라는 점을 알아주셨으면 좋겠습니다.
Background
지금까지 저희는 다양한 어텐션 기반 모델들을 보았습니다. 하지만 이러한 어텐션 블록을 모델에 적용한다고 하더라도 문제는 항상 효과적이고 설명가능하지 않다 (예를 들어 백그라운드에 가중치가 많이 들어가는 경우를 의미하는 거 같습니다.)는 문제점이 존재합니다. 이러한 문제를 해결하기 위해 Attention-Augmented (AA) ResNet에서는 Transformer에서 활용되는 Self-Attention 매커니즘을 CNN에 결합하여 해결하기도 하였죠. 본 논문에서는 이와 같이 AA ResNet에서 사용되는 Self-Attention 매커니즘을 개선하는 방법에 대해서 제안합니다.
이를 위해 본 논문에서는 Evolving Mechanism을 고려합니다. 쉽게 말해 어텐션 맵을 한번 뽑고 안쓰는 것이 아니라 이후 어텐션 맵을 만들 때 같이 활용하여 보다 정확한 어텐션 맵이 만들어 질 수 있도록 점점 발전시키게 되는 것이죠. 특히, 이에 대한 동기는 기본적으로 Transformer 및 CNN 모델에서 어텐션 맵이 각 계층별로 독립적으로 학습된다라는 것에서 문제점을 삼고 시작합니다. 그렇다고 해서 모든 계층에서 동일한 어텐션 맵을 사용하게 되면 (즉 가중치 공유) 계층의 깊이 별로 필요한 추상적 특징이 다를 것이기 때문에 성능으 떨어질 것으로 예상해볼 수 있습니다. 이러한 문제를 해결하기 위해 Evoluving Mechanism을 제안하여 어텐션 맵을 점점 개선하는 것이죠.
본 논문의 기여도를 정리하면 다음과 같습니다.
- Evolving Attention (EA) Mechanism 제안
- EA 기반 모델은 residual convolution module의 연속적인 연결로 구성되어 어텐션 맵을 점차 개선하게 됨
- 각 계층 간 residual link를 적용함으로써 어텐션 맵이 각 토큰 간 관계성의 정보 흐름을 활용할 수 있음
Evolving Attention Transformer
1) Overview
$\mathbf{x} \in \mathbb{R}^{N \times C}$를 시퀀스 길이 $N$ 그리고 차원 $C$인 텍스트 시퀀스라고 가정하겠습니다. 만약 영상이라면 $\mathbf{x} \in \mathbb{H \times W \times C}$와 같이 주어졌을 때 $N = HW$와 같이 flattening과 linear projection 과정을 거쳐주면 모두 Transformer에 넣을 수 있게 됩니다.

이전 Background에서도 설명드렸지만 그림 2에서 보이시는 것과 같이 기존 Transformer 구조에서는 Self-Attention 매커니즘은 각 계층 별로 서로 다르게 학습되기 때문에 일반화 능력이 떨어진다는 점을 본 논문에서는 핵심 문제로 삼았습니다. 따라서, 각 계층의 어텐션 맵 끼리의 연결성을 도입하여 이러한 문제를 해결한다는 것이 핵심입니다.
2) Attention Map Generation
일단 Attention Map Generzation은 기존 Transformer의 과정과 거의 동일하기 때문에 특별히 설명할 것은 없습니다. 다만, Absolution Positional Encoding을 수행하는 경우와 Relative Positional Encoding을 수행하는 경우로 나누어 설명을 진행하는 데 여기서는 크게 중요하지 않으므로 넘어가도록 하겠습니다.
STEP1. Query $\mathbf{Q}$와 Key $\mathbf{K}$를 두 개의 linear projection parameter $\mathbf{W}^{Q}$와 $\mathbf{W}^{K}$를 통해 linear projection 수행
$$\begin{cases} \mathbf{Q} &= \mathbf{X}\mathbf{W}^{Q} \\ \mathbf{K} &= \mathbf{X} \mathbf{W}^{K} \end{cases}$$
STEP2-a. (Absolution Positional Encoding 경우) 어텐션 맵 생성
$$\mathbf{A} = \text{Attention} (\mathbf{X}) = \text{Softmax} (\frac{\mathbf{Q} \mathbf{K}^{T}}{\sqrt{d}})$$
STEP2-b. ( Relative Positional Encoding 경우) 어텐션 맵 생성
$$\mathbf{A} = \text{Attention} (\mathbf{X}) = \text{Softmax} (\frac{\mathbf{Q} \mathbf{K}^{T}}{\sqrt{d}} + \mathbf{R})$$
3) Attention Map Convolution
본 논문의 제일 핵심 파트라고 보시면 될 거 같습니다. 해당 과정에서 서로 인접한 블록으로부터 얻은 어텐션 맵 간의 residual connection을 적용하는 과정이 존재합니다.
일단, 각 계층에서는 총 $K$개의 head가 존재한다고 가정하겠습니다. 따라서 각 head 별로 모두 어텐션 맵을 만들기 때문에 총 $K$개의 어텐션 맵이 나온다는 것을 알 수 있습니다. 따라서 저희는 3차원 텐서 $A \in \mathbb{R}^{N \times N \times K}$가 있다고 가정할 수 있죠. 즉, 저희는 어텐션 맵을 $N \times N$ 크기와 $K$개의 채널을 가지는 영상 데이터로써 해석할 수 있다는 의미입니다. 따라서, 해당 어텐션 맵 $A$를 통해 보다 개선된 어텐션 맵을 얻는 것이 목표가 될 것 입니다. 출력 어텐션 맵도 역시 각 Multi-Head Self-Attention을 적용해야하기 때문에 $K$개가 출력되어야합니다. 따라서, 입력된 $K$개의 어텐션 맵을 통해 서로 정보를 교환하는 과정이 존재하기 때문에 일반화된 어텐션 맵을 얻을 수 있게 되는 것이죠.
이 과정을 수식적으로 표현하면 다음과 같습니다.
$$\begin{cases} \mathbf{A}^{i}_{\text{input}} &= \alpha \cdot \mathbf{A}^{i - 1}_{\text{logit}} + (1 - \alpha) \cdot \text{Attention} (\mathbf{X})^{i}_{\text{logit}} \\ \mathbf{A}^{i}_{\text{logit}} &= \beta \cdot \text{CNN} (\mathbf{A}^{i}_{\text{input}}) + (1 - \beta) \cdot \mathbf{A}^{i}_{\text{input}} \\ \mathbf{A}^{i} &= \text{softmax} (\mathbf{A}^{i}_{\text{logit}}) \end{cases}$$
여기서 $\mathbf{A}^{i - 1}_{\text{logit}}$은 이전 블록으로부터 얻은 어텐션 맵을 의미합니다. 그리고 $\text{Attention} (\mathbf{X})^{i}_{\text{logit}}$은 현재 블록에서 얻은 어텐션 맵이죠. 이제 두 결과의 가중합을 통해 저희는 Attention Map Generation의 입력 텐서인 $\mathbf{A}^{i}_{\text{\logit}}$을 얻을 수 있게 됩니다. 다음으로 $\text{CNN} (\cdot)$과 residual connection을 통해 새로운 어텐션 맵을 최종적으로 얻을 수 있게 되는 것이죠. 이 때 사용되는 $\alpha, \beta \in [0, 1]$은 하이퍼파라미터로 두 경로 간 정보 흐름을 통제하는 역할을 수행합니다.
4) Value Projection and Feed-Forward Layers
드디어 마지막 단계입니다. 사실 이부분도 기존의 Transformer와 동일하기 때문에 간단하게 수식만 보여드리고 넘어가도록 하겠습니다.
- Value Projection
$$\begin{cases} \mathbf{H}_{k} &= \mathbf{A}_{k} \mathbf{X} \mathbf{W}_{k}^{V} \\ \mathbf{H} &= ( \mathbf{H}_{1} \oplus \mathbf{H}_{2} \oplus \cdot \oplus \mathbf{H}_{K} )\mathbf{W}^{O} \end{cases}$$
- Feed-Forward Layers
$$\text{EA-Transformer} (\mathbf{X}) = \text{ReLU} (\mathbf{H} \mathbf{W}_{1} + \mathbf{b}_{1}) \mathbf{W}_{2} + \mathbf{b}_{2}$$
Experimental Results
1) ImageNet-1K Classification


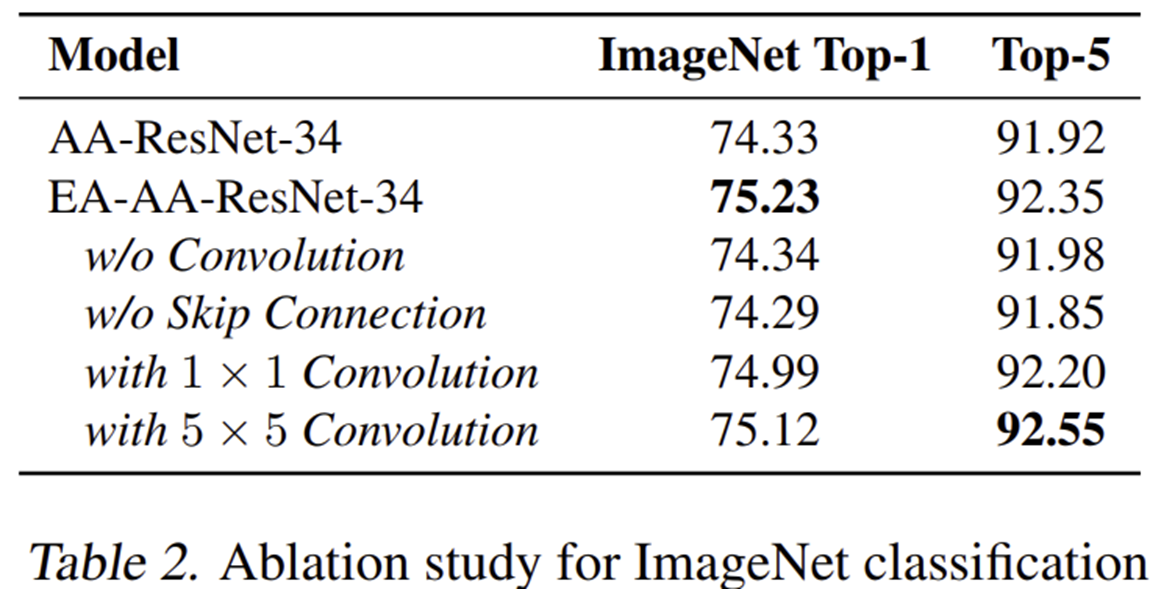
2) Ablation Study