안녕하세요. 지난 포스팅의 [Transformer] CvT: Including Convolutions to Vision Transformer (ICCV2021)에서는 MSA 단계에서 Depth-wise Separable Convolution을 사용하는 CvT에 대해서 알아보았습니다. 이를 통해 Transformer에게 부족했던 inductive bias 중 locality를 주입해줄 수 있기 때문에 positional encoding에서 자유로워 질 수 있었죠. 오늘은 이와 유사하게 접근하여 Convolution layer를 사용하는 CeiT에 대해 소개시켜드리도록 하겠습니다.
Incorporating Convolution Designs into Visual Transformers
Motivated by the success of Transformers in natural language processing (NLP) tasks, there emerge some attempts (e.g., ViT and DeiT) to apply Transformers to the vision domain. However, pure Transformer architectures often require a large amount of trainin
arxiv.org
Background
기본적으로 ViT는 JFT-300M이나 ImageNet-22K와 같은 large-scale 데이터셋에 의존하기 때문에 실질적으로 새로운 데이터셋에 대한 학습을 적용하기 어렵습니다. 또한, DeiT는 teacher 모델과 distillation type에 따른 성능 변화가 너무 크기 때문에 적절한 조합을 찾는 것이 중요합니다. 공통적으로 ViT과 DeiT는 컴퓨터 비전 관련 문제를 해결하는 데 있어 중요한 inductive bias가 부족합니다.
따라서, 본 논문은 CvT와 유사하게 CNN의 inductive bias를 Transformer에 주입해주기 위한 모델인 Convolution-enhanced image Transformer (CeiT)를 제안합니다. 해당 모델은 CNN을 이용한 패치 추출단계인 Image-to-Token (I2T)를 도입하여 low-level feature를 Transformer가 활용할 수 있도록 합니다. 또한, MSA 단계에서 인접 토큰 간 관계성을 강화시킬 수 있는 Locally-enhanced Feed-Forward (LeFF), 그리고 mutli-level representation power를 향상시키기 위한 Layer-wise Class Token Attention (LCA)도 도입하였습니다. 이를 통해 ImageNet-1K에서 학습된 CeiT는 lightweight하고 efficient한 모델일 뿐만 아니라 state-of-the-art 성능을 달성하였습니다. 본 논문의 핵심 기여도를 정리하면 다음과 같습니다.
- CNN (Extract Low-level feature, Strengthen Locality)과 Transformer (Long-range Dependencies)의 장점을 결합한 CeiT를 제안
- Image-to-Token (I2T), Locally-enhanced Feed-Forward (LeFF), 그리고 Layer-wise Class Token Attention (LCA)를 결합
- ImageNet-1K에서 학습된 CeiT는 lightweight하고 efficient한 모델일 뿐만 아니라 state-of-the-art 성능을 달성

Revisiting Vision Transformer
이번 절에서는 기존의 ViT에서 수행되는 연산들인 Tokenization, Encoder Block, MSA, 그리고 FFN 순으로 좀 더 자세하게 분석하고 단점을 알아보겠습니다.
1) Tokenization
첫번째 단계인 Tokenization은 입력 영상을 패치 단위로 나누는 패치화 (patchify) 단계입니다. 먼저, 입력 영상 $\mathbf{x} \in \mathbb{R}^{H \times W \times 3}$을 2D 패치 $\mathbf{x}_{p} \in \mathbb{R}^{N \times (P^{2} \times 3)}$로 나누어줍니다. 이때, $(H, W)$는 입력 영상의 해상도, $(P, P)$는 추출된 패치의 해상도, 그리고 $N = \frac{HW}{P^{2}}$으로 입력 영상으로부터 패치를 추출했을 때 나오는 패치의 개수를 의미합니다. 다음으로 각 패치들을 모두 flatten 시켜 벡터로 만들어준 뒤 linear projection을 통해 $C$개의 벡터 요소를 가지도록 매핑합니다. 그리고 class token $\mathbf{x}_{t} \in \mathbb{R}^{C}$를 추가해줍니다.
하지만, 이와 같이 추출된 패치는 패치간 관계성이 존재하지 않을뿐만 아니라 영상으로부터 저수준 특징을 얻을 수 없습니다. 실제로 ViT 논문에서도 대용량의 데이터셋을 이용해서 학습해야지만 CNN과 같은 저수준 특징을 학습할 수 있다는 것을 언급하였죠.
2) Encoder Block
기본적으로 Transformer의 Encoder Block은 MSA와 FFN으로 구성되어 다음과 같은 연산을 수행합니다.
$$\begin{cases} \mathbf{x}^{'} &= \text{LN} (\mathbf{x} + \text{MSA} (\mathbf{x})) \\ \mathbf{y} &= \text{LN} (\mathbf{x}^{'} + \text{FFN} (\mathbf{x}^{'})) \end{cases}$$
보시면 이 과정에서 sub-layer 간의 residual connection과 layer normalization이 포함되어 있는 것을 볼 수 있죠. 해당 Encoder Block을 이용하면 아쉽지만 receptive field를 효과적으로 늘릴 수 없기 때문에 ViT의 최적화 효율성을 방해할 수 있을 것이라는 것이 본 논문의 주장입니다.
3) MSA
Encoder Block 내의 첫번째 sub-layer인 MSA를 이해하기 위해서는 self-attention (SA)을 이해해야합니다. SA에서는 입력 토큰 $\mathbf{x}_{t} \in \mathbb{R}^{(N + 1) \times C}$를 입력받아 qkv 벡터 공간으로 맵핑시켜준 뒤 다음과 같은 연산을 수행하죠.
$$\text{Attention} (\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax} \left( \frac{\mathbf{Q}\mathbf{K}^{T}}{\sqrt{C}} \right) \mathbf{V}$$
여기서 $\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{(N + 1) \times C}$입니다. MSA는 위 SA를 여러 개의 Multi-head로 쪼개어 각각 SA를 적용하는 것을 의미합니다. 이는 CNN에서 추출된 각 특징 맵이 서로 다른 다양한 특징을 추출할 수 있도록 하는 것과 어느정도 일맥상통한다고 볼 수 있습니다.
4) FFN
Encoder Block 내의 두번째 sub-layer인 FFN입니다. 다음과 같이 MSA를 이용해 similiarity를 기반으로 long-range dependency를 얻은 토큰을 기반으로 연산을 다음과 같이 한번 더 수행하죠.
$$\text{FFN} (\mathbf{x}) = \sigma (\mathbf{x} \mathbf{W}_{1} + \mathbf{b}_{1}) \mathbf{W}_{2} + \mathbf{b}_{2}$$
여기서 $\mathbf{W}_{1} \in \mathbb{R}^{C \times K}, \mathbf{W}_{2} \in \mathbb{R}^{K \times C}, \mathbf{b}_{1} \in \mathbb{R}^{K}, \mathbf{b}_{2} \in \mathbb{R}^{C}$의 형상을 가집니다. 이 단계는 컴퓨터 비전 관련 문제에서 중요한 토큰 (패치) 간 공간적 관계성을 이해할 수 없습니다. 이러한 단점은 ViT가 inductive bias를 얻기 위해 대량의 데이터셋이 필요로 해지는 문제점으로 귀결됩니다.
Convolution-enhanced image Transformer (CeiT)
방금과 같이 위에서 언급한 ViT를 이용해서 컴퓨터 비전 문제를 풀 때 발생하는 문제점들을 해결하기 위해 본 논문에서는 convolution 연산과 Transformer를 결합한 CeiT를 제안합니다. Background에서 언급드렸다싶이 해당 모델은 기본적으로 3가지의 핵심 모듈인 Image-to-Token (I2T), Locally-enhanced Feed-Forward (LeFF), 그리고 Layer-wise Class Token Attention (LCA)로 구성되어 있습니다. 이제부터는 각 모듈에 대해 좀 더 상세하게 분석해보도록 하겠습니다.
1) Image-to-Token (I2T)

첫번째로 I2T 모듈입니다. 기존의 ViT는 위 그림에서 Split 과정을 거쳐 여러 개의 패치로 쪼갠 뒤 Linear Projection을 통해 embedding을 시켜주죠. 하지만, CeiT에서는 처음에 입력 영상에 convolution 연산을 적용하여 얻은 특징 맵을 기반으로 패치를 추출하게 됩니다. 이러한 단계를 통해 CNN의 장점 중 하나인 low-level feature를 추출 할 수 있는 능력을 얻게 될 뿐만 아니라 패치의 크기도 max pooling 단계를 통해 줄여줌으로써 훈련 단계의 어려움을 한층 더 줄여줍니다. 이 과정은 다음과 같은 수식을 따릅니다.
$$\mathbf{x}^{'} = \text{I2T} (\mathbf{x}) = \text{MaxPool} (\text{BN} (\text{Conv} (\mathbf{x})))$$
여기서 $\mathbf{x}^{'} \in \mathbb{R}^{\frac{H}{S} \times \frac{W}{S} \times D}$로 $S$와 $D$는 각각 합성곱 연산의 stride 파라미터와 합성곱 연산을 통해 나온 채널의 개수를 의미합니다. 본 논문에서는 ViT에서 얻는 토큰의 개수와 CeiT를 통해 얻는 토큰의 개수를 동일하게 맞추기 위해 $S = 4$로 고정하였습니다.
2) Locally-enhanced Feed-Forward (LeFF) Network
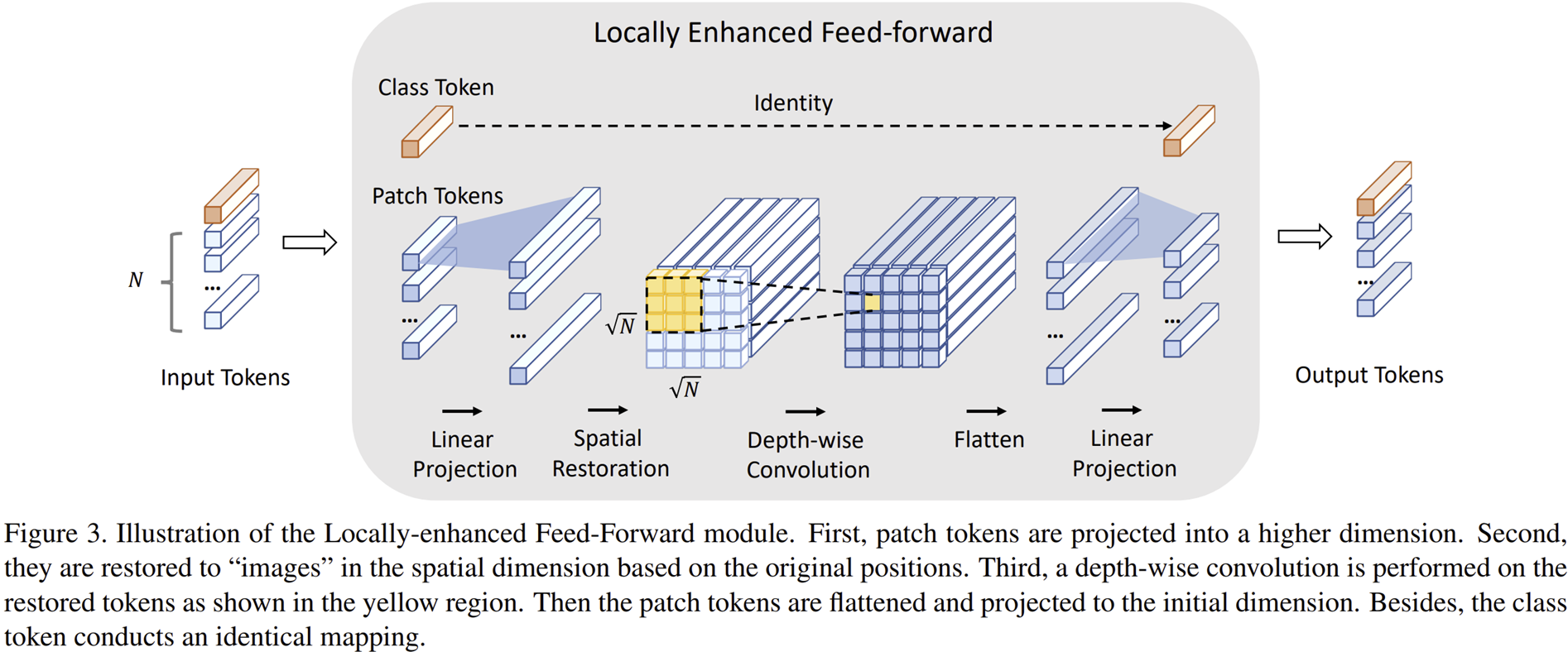
그림 3은 LeFF의 전체적인 구조를 보여주고 있습니다. 이는 CNN의 장점인 local information의 추출능력과 Transformer의 장점인 long-range dependency를 결합하기 위해 제안된 모듈로 다음과 같은 단계로 진행합니다.
STEP1. 첫번째 Linear Projection 적용
이전 MSA 모듈로 부터 입력 토큰 $\mathbf{x}_{t}^{h} \in \mathbb{R}^{(N + 1) \times C} $이 주어졌을 때 패치 토큰 $\mathbf{x}_{p}^{h} \in \mathbb{R}^{N \times C}$와 클래스 토큰 $\mathbf{x}_{c}^{h} \in \mathbb{R}^{C}$로 나누어줍니다. 다음으로 패치 토큰 $\mathbf{x}_{p}^{h}$에만 linear projection을 적용하여 더 큰 차원으로 매핑시켜 $\mathbf{x}_{p}^{l_{1}} \in \mathbb{R}^{N \times (e \times C)}$로 만들어 줍니다. 여기서 $e$는 CeiT의 핵심 하이퍼파라미터로 expantion ratio라고 부르겠습니다.
STEP2. Spatial Restoration
이제 토큰을 다시 영상처럼 다루기 위해 $N$개의 토큰을 재배열하여 $\sqrt{N} \times \sqrt{N}$ 크기의 모양을 가질 수 있도록 합니다. 이를 $\mathbf{x}_{p}^{s} \in \mathbb{R}^{\sqrt{N} \times \sqrt{N} \times (e \times C)}$라고 하죠.
STEP3. Depth-wise Convolution 적용
3D 영상 (채널 포함)으로 변환된 토큰은 이제 합성곱 연산을 통해 local information을 추출할 수 있게 됩니다. 이때 좀 더 효율적으로 이 과정을 수행하기 위해 $k \times k$크기의 커널의 크기를 가지는 Depth-wise convolution을 활용합니다. 현재 토큰 위치를 기준으로 주변 $k^{2} - 1$개의 토큰들간의 representation correlation을 향상시킬 수 있게 됩니다. 이렇게 얻은 특징 맵을 $\mathbf{x}_{p}^{d} \in \mathbb{R}^{\sqrt{N} \times \sqrt{N} \times (e \times C)}$라고 하겠습니다.
STEP4. Flattening feature map
이제 다시 토큰으로 변환해주기 위해 flatten을 적용하여 $\mathbf{x}_{p}^{f} \in \mathbb{R}^{N \times (e \times C)}$로 만들어줍니다.
STEP5. 두번째 Linear Projection 적용 및 class token과 결합
다음으로 원래 크기의 채널 개수로 변환해주기 위해 다시한번 더 linear projection을 적용하여 $\mathbf{x}_{p}^{l_{2}} \in \mathbb{R}^{N \times C}$로 줄여줍니다. 그리고 분리되어 있던 class token $\mathbf{x}_{c}^{h}$와 결합하여 출력 토큰 $\mathbf{x}_{t}^{h + 1} \in \mathbb{R}^{(N + 1) \times C}$을 얻게 됩니다.
위 단계를 수식으로 나타내면 다음과 같습니다.

3) Layer-wise Class-Token Attentoin (LCA)

그림 4는 LCA의 전체적인 블록 다이어그램을 보여주고는 있지만 조금 이해하기 어렵습니다. 이를 이해하기 위해서는 좀 더 자세한 제안 동기가 필요하죠. 기본적으로 CNN은 계층이 깊어질수록 receptive field가 증가하게 되어 더욱 넓은 영역의 특징을 이해할 수 있습니다. 따라서 컴퓨터 비전 문제에 활용되기 아주 알맞죠. 하지만 ViT에서는 어떨까요? 본 논문에 따르면 ViT는 CNN과 유사하게 Attention Distance가 늘어난다는 점을 확인하였습니다. 즉, stage가 진행될 수록 더욱 긴 영역에 대한 global dependency를 이해할 수 있게 되는 것이죠. 그렇다면 이와 같이 다양한 attention distance를 가지는 토큰들을 모아 attention을 시켜준다면 좀 더 Transformer의 장점을 부각해볼 수 있지 않을까요? 이를 위해 제안된 것이 바로 LCA입니다.
하지만 여기서 중요한 것은 LCA에서는 패치 토큰을 사용하지 않고 각 계층의 클래스 토큰을 사용한다는 점입니다. 이는 기본적으로 클래스 토큰에서는 Transformer의 represention correlation이 집약되어 있다고 가정하기 때문에 가능하죠.
먼저, 각 계층의 토큰들을 하나로 모은 $\mathbf{X} = [ \mathbf{x}_{c}^{(1)}, \dots, \mathbf{x}_{c}^{(l)}, \dots, \mathbf{x}_{c}^{(L)} ]$을 정의합니다. 이때 한 가지 더 강조하고 싶은 것은 "마지막 계층의 클래스 토큰 $\mathbf{x}_{c}^{(L)}$"를 중심으로 다른 계층의 클래스 토큰들과의 representation correlation을 확인하죠. 이를 통해 원래 $\mathcal{O} (n^{2})$일 연산이 $\mathcal{O} (n)$으로 감소하게 됩니다.
4) Model Variants

CeiT 역시 기존 Transformer 모델들과 마찬가지로 규모에 따라 변형 구조를 만들어 각각 CeiT-T, CeiT-S, CeiT-B를 만들어제시합니다.
Experiment Results


본 논문에서는 실험에서 사용한 데이터셋에 대한 정보와 학습 셋팅을 모두 표 2와 표 3에 정리하였습니다.

표 4는 CNN 기반 모델들과 Transformer 기반 모델들과의 비교를 하고 있습니다. 결론적으로 모든 모델들 통들어서 가장 높은 성능을 보여주고 있습니다. 특히, ViT와 비교했을 때 FLOPs과 Params가 극단적으로 감소하였지만 성능은 거의 비슷하거나 더 높은 것을 볼 수 있습니다.

뿐만 아니라 ImageNet에 학습된 모델을 Downstream task에도 적용해보며 성능을 확인합니다. 결과적으로 pre-trained 모델을 활용했을 때 CeiT가 전체적으로 높은 결과를 보여주고 있습니다.
