안녕하세요. 지난 포스팅의 [IC2D] MNASNet: Platform-Aware Neural Architecture Search for Mobile (CVPR2019)에서는 실제 모바일 디바이스에서 inference latency를 구함으로써 좀 더 정확한 NAS를 수행할 수 있는 MNAS에 대해서 소개하였습니다. 그나저나 다들 설날을 잘 보내셨나요? 저는 오늘도 연구실에 남아 논문을 읽고 있습니다. ㅎㅎ 이 김에 재밌는 논문하나 소개할까합니다. 오늘 리뷰할 논문은 NIPS 2018년에 게재 승인된 Gather-Excite Block입니다.
Gather-Excite: Exploiting Feature Context in Convolutional Neural Networks
While the use of bottom-up local operators in convolutional neural networks (CNNs) matches well some of the statistics of natural images, it may also prevent such models from capturing contextual long-range feature interactions. In this work, we propose a
arxiv.org
Background
해당 논문의 기본적인 컨셉은 SE Block의 일반화입니다. SE Block에서 수행하는 Squeenze 연산은 입력된 특징 맵에 Global Average Pooling을 적용하여 각 벡터 요소가 채널 설명자 (channel descriptor)의 역할을 할 수 있도록 변환해줍니다. 그리고 Excitation 연산은 추출된 채널 설명자들간의 상호정보를 이해함으로써 채널의 값을 재조정 (recalibration)해주는 역할을 하죠. 오늘 소개하는 Gather-Excite (GE) Block은 특히, Squeece 연산을 일반화시킬 수 있는 몇 가지 방법에 대해 소개합니다.
본 논문의 핵심 기여는 다음과 같이 정리할 수 있습니다.
- SE Block보다 효율적인 GE Block을 제시
- GE Block은 SE Block과 유사하게 입력 특징 맵에서 contextual information을 추출할 수 있는 Gather 연산과 추출된 aggregation을 기반으로 특징 맵을 재조정하는 Excite 연산으로 구성
- 최소한의 하이퍼파라미터 튜닝으로 다양한 딥 러닝 모델, 데이터셋, task에서 높은 성능을 달성
The Gather-Excite Framework

그림 1은 GE Block의 전체적인 구조를 보여주고 있습니다. 언뜻보면 SE Block과 별 차이가 없어보입니다. 여기서 핵심은 Gather 연산인 $\xi_{G}$와 Excite 연산인 $\xi_{E}$을 어떻게 정의하느냐에 따라서 SE Block과 동일해질수도 있고 완전히 새로운 모듈이 될 수도 있다는 점에서 SE Block의 일반화된 모형이라고 부를 수 있을 거 같습니다.
1). Gather Operation $\xi_{G}$
Gather 연산 $\xi_{G}$의 목적은 입력 특징 맵에 대해 spatial extent $e$라는 하이퍼파라미터를 도입하여 뉴런의 반응정도를 하나로 집계하는 것입니다. 쉽게 말해 spatial extent $e$가 만약 특징 맵의 크기와 동일하게 정의된다면 이는 global extent로 바뀌게 되며 SE Block의 Squeeze 연산인 Global Average Pooling과 같은 연산이 되는 것이죠. 이를 좀 더 자세하게 공식화시켜보도록 하겠습니다.
먼저, $x = \{ x^{c} | c \in \{ 1, 2, \dots, C \} \}$를 $C$개의 채널을 가진 특징 맵이라고 가정하겠습니다. 그리고 $\iota (u, e) = \{ eu + \delta | \delta \in \left[ -\lfloor \frac{2e - 1}{e} \rfloor, \lfloor \frac{2e - 1}{2} \rfloor \right]^{2} \}$를 selection operator라고 정의하겠습니다. 이를 통해 저희는 Gather 연산 $\xi_{G}: \mathbb{R}^{H \times W \times C} \rightarrow \mathbb{R}^{H^{'} \times W^{'} \times C}$는 임의의 입력 특징 맵 $x$가 다음 조건을 만족하는 함수로 정의해볼 수 있습니다. 여기서, $H^{'} = \lfloor \frac{H}{e} \rfloor$과 $W^{'} = \lfloor \frac{W}{e} \rfloor$입니다.
$$\xi_{G} (x)^{c}_{u} = \xi_{G} ( x \odot \mathbf{1}_{\iota (u, e)}^{c} )$$
여기서 $\mathbf{1}_{\{\cdot\}}$은 indicator function 그리고 $\odot$은 원소별 곱 (또는 아마다르 곱)을 의미합니다. 또한, $u \in \{ 1, \times, H^{'} \} \times \{ 1, \dots, W^{'} \}$입니다. 해당 수식을 이해하기 위해 $\iota (u, e)$부터 간단한 예시를 통해 이해해보겠습니다. 쉽게 하기 위해 $u = (1, 1)$ 그리고 $e = 2$라고 가정하겠습니다. 그러면 $\iota$는 다음과 같이 정의되겠죠?
$$\iota ((1, 1), 2) = \{ 2 \cdot (1, 1) + \delta | \delta \in \left[ -1, 1 \right] \times \left[ -1, 1 \right] \}$$
따라서, $\iota ((1, 1), 2) = \{ (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3) \}$을 가지게 됩니다. 즉, $\iota ((1, 1), 2)$라는 것은 왼쪽 상단 좌표값 $(1, 1)$을 기준으로 이웃 픽셀의 거리가 $e = 2$가 되는 좌표를 찾는 것과 동일하게 됩니다.
이렇게 복잡하게 설명했지만 결국 쉽게 보자면 그림 1의 왼쪽 입력 특징맵에서 살짝 연하게 그려진 부분의 좌표를 표시한 것이 바로 $\iota (u, e)$입니다. 이를 통해, 각 영역은 $(2e - 1)^{2}$만큼의 receptive field를 가지게 됩니다. 그리고 해당 receptive field가 입력 특징 맵의 해상도와 동일해진다면 이는 global extent를 추출하는 것과 동일합니다.
2). Excite Operation $\xi_{E}$
Excite 연산 $\xi_{E}$의 목적은 추출된 contextual feature를 이용하여 입력 특징 맵의 채널을 재조정하는 것으로 다음과 같이 정의할 수 있습니다.
$$\xi_{E} (x, \hat {x}) = x \odot f(\hat{x})$$
여기서 $f: \mathbb{R}^{H^{'} \times W^{'} \times C} \rightarrow [0, 1]^{H \times W \times C}$와 같이 정의되는 함수입니다.
Models and Experiments
이번 절에서는 GE Block의 세 가지 변형 구조를 실험 및 평가하게 됩니다. 기본적으로 ImageNet을 사용하였으며 실험 셋팅은 다음과 같습니다.
- Dataset
- ImageNet-1K: 1.28 million training images & 50K validation images with 1,000 classes
- Data Augmentation (Same as InceptionNet)
- Optimization: Stochastic Gradient Descent
- momentum: 0.9
- weight decay: -
- learing rate: initial learning rate is set to 0.1 and is reduced by a factor of 10 each time the loss plateaus
- batch size: 256
- epochs: 300 (100 에폭보다 성능으로는 더 좋았다고 함)
- GPU 타입 명시 X
1). Parameter-free Pairing
GE Block과 같이 일반화된 모듈의 장점은 저희가 원하는 대로 다양한 구조를 생각해볼 수 있다는 점 입니다. 특히, resource-constrained environment를 고려할 때 보다 효율적으로 동작할 수 있도록 하기 위해 Gather 연산 $\xi_{G}$와 Excite 연산 $\xi_{E}$ 모두 파라미터가 없는 연산으로 고려해볼 수 있습니다. 이를 GE-$\theta^{-}$로 표기하며 다음과 같이 정의됩니다.
$$y^{c} = x \odot \sigma (\text{interp} (\xi_{G} (x)^{c}))$$
여기서 Gather 연산 $\xi_{G}$은 selection operator $\iota (u, e)$를 통해 선택된 영역만큼에 대한 평균 풀링으로 정의합니다. 그리고 Excite 연산 $\xi_{E}$는 resize + sigmoid + multiplication의 조합으로 구성된 연산으로 정의되죠.
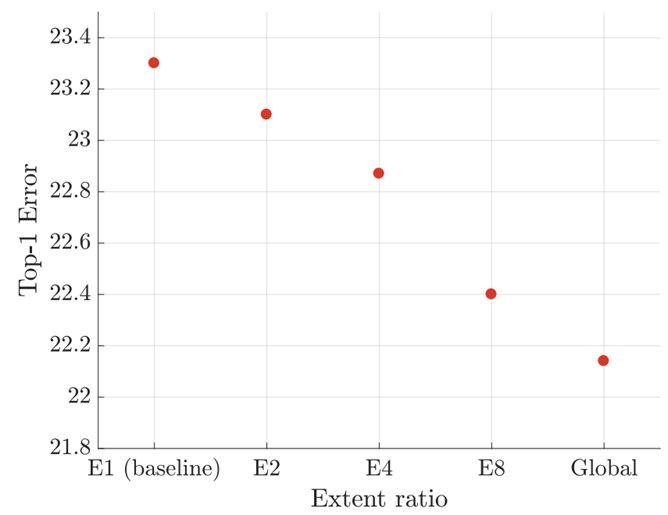
위 그림은 extent ratio $e$에 따른 ImageNet에서의 에러율을 보여주고 있습니다. $e$가 커질수록 입력 특징 맵 내의 전체적인 특징을 얻을 수 있기 때문에 성능 향상을 얻을 수 있는 것으로 보입니다.
2). Parameterized Pairing
이번에는 Gather 연산을 파라미터가 존재하는 연산으로 바꾸도록 하겠습니다. 이를 위해 $\xi_{G}$를 Depti-wise Convolution으로 정의하여 보다 효율적으로 수행합니다. Excite 연산 $\xi_{E}$은 GE-$\theta^{-}$와 동일합니다. 이와 같은 설정을 GE-$\theta$라고 하도록 하죠.
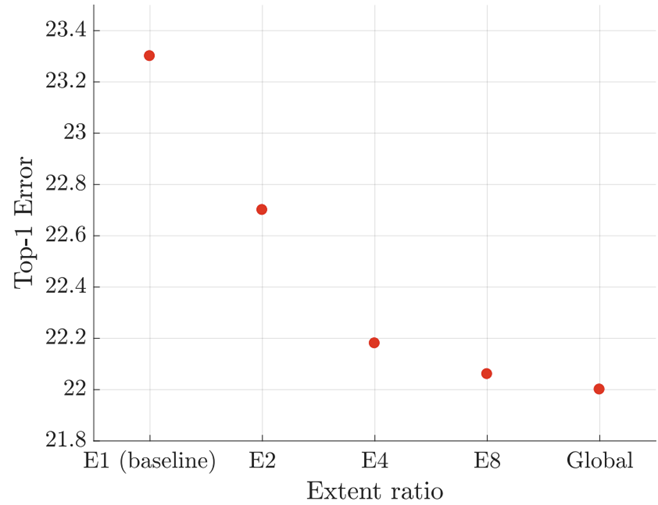
GE-$\theta^{-}$와 마찬가지로 성능이 Global extent일 수록 향상되고 있는 것을 볼 수 있으며 전체적으로는 GE-$\theta^{-}$ 보다는 성능이 높은 것을 볼 수 있죠.

표 1에서는 GE-$\theta$가 어떤 stage에 넣을 때 성능이 크게 향상되는 지 확인합니다. 실제로 중간 stage와 마지막 stage에서 GE-$\theta$을 넣었을 때 성능이 가장 크게 향상되는 것을 볼 수 있습니다. 또한 파라미터 증가량도 상대적으로 작은 것을 볼 수 있죠?


SE Block과 마찬가지로 Fully-Connected Layer 기반의 Excite 연산을 적용하는 GE-$\theta^{+}$도 성능을 확인합니다. 결과적으로 SE Blcok보다 성능이 약간 향상된 것을 볼 수 있죠.

표 4는 ResNet-50보다 더 lightweight 모델인 ShuffleNet에 SE Block과 GE Block을 넣었을 때 성능을 확인합니다. 여기서 GE Block은 기존의 SE Block보다 약 1.1%로 훨씬 높은 성능을 보여주고 있습니다.
