안녕하세요. 지난 포스팅의 [IC2D] Residual Attention Network for Image Classification에서는 CNN에서 어텐션 (attention)이라는 개념을 도입한 RAN에 대해서 소개시켜드렸습니다. 오늘은 MobileNet에 이어 효율성을 극한으로 강조한 논문인 ShuffleNet에 대해서 소개해드리도록 하겠습니다.
Background
최근 나온 수많은 합성곱 기반의 신경망들은 인간의 한계를 뛰어넘어 ILSVRC 대회에서도 굉장히 높은 성능을 보여왔습니다. 하지만, 이러한 모델이 발전될 수록 그만큼 연산량 및 복잡도가 크게 증가하기 때문에 이를 실생활에서 활용하기는 어려운 측면이 있었습니다. 이와 같은 문제를 해결하기 위해 모델을 단순하게 만드는 pruning, compressing, low-bit representing과 같은 방법들이 제안되어왔습니다. 이 중에서도 MobileNet은 모델을 단순하게 만드는 방법 중 가장 유명하고 기초적인 방법이 되었죠. 본 논문에서는 MobileNet의 depthwise separable convolution을 개선하는 것을 목표로 두고 2가지 새로운 연산을 제안합니다. 첫번째는 pointwise group convolution 이고 두번째는 channel shuffle operation이죠. 두 개의 연산이 결합된 ShuffleNet은 기존의 MobileNet보다 적은 적은 연산량으로 훨씬 높은 성능 향상을 달성합니다.
Approach
1). Channel Shuffle for Group Convolution
MobileNet과 Xception 모두 depthwise separable convolution을 사용하고 ResNext에서는 group convolution을 도입하여 효율적인 모델을 만들었습니다. 하지만, 3가지 모델 모두 $1 \times 1$ 합성곱 계층의 장점을 살리 수 없었죠. 기본적으로 $1 \times 1$ 합성곱 계층은 입력 특징맵의 전체 채널 간 상관계수를 추출하는 것을 목표로합니다. 하지만, 위 3개의 모델들은 모두 중간에 특징맵을 그룹으로 나누어 연산하기 때문에 제한적인 개수의 채널 간 상관계수만을 추출할 수 있습니다.

그림1은 이 문제를 정확하게 설명해주고 있습니다. (a)는 기존의 group convolution을 여러 번 적용했을 때 특징 맵의 모습입니다. $g = 3$으로 나누었기 때문에 3개의 색으로 표현됩니다. 이미 각 group으로 나누어진 특징 맵들은 서로의 상관성이 점점 사라지면서 그룹 별로 상이한 특징을 얻게 됩니다. 이는 효율적인 모델에서 다양한 특징 맵을 추출해야하는 측면에서 성능하락의 주원인이 됩니다.
ShuffleNet은 이 문제를 아주 단순한 방법으로 해결합니다. (b)를 보시면 첫번째 단계에서 3개의 group으로 나뉘어 합성곱 연산이 진행되어 각 그룹은 서로 다른 특징 맵을 가지게 됩니다. 여기까지는 (a)와 동일하지만 다음 계층부터는 각 채널이 3개의 group으로 다시 나뉘어서 섞이는 (shuffling) 과정이 추가됩니다. 이렇게 되면 (c)와 같이 섞이기 때문에 각 group은 이전 계층의 모든 group들의 특징 맵을 포함하고 있어 보다 풍부한 표현력을 가지게 됩니다. 이러한 연산을 channel shuffle이라고 정의합니다.
2). ShuffleNet Unit

ShuffleNet은 여기에서 유연하게 다른 모델에 적용할 수 있도록 블록 단위의 새로운 unit을 제안합니다. 그림 2의 (a)는 단순히 depthwise convolution을 적용했을 때 모습니다. (b)부터 ShuffleNet에서 사용하는 블록이 입니다. 달라진 점은 입력 시 $1 \times 1$ 그룹 합성곱, 즉 pointwise group convolution이 적용된 뒤 channel shuffle을 통해 특징 맵의 표현력을 증가시킨 뒤 depthwise convolution이 입력합니다. 마지막으로 pointwise group convolution을 한번 더 적용하여 하나의 residual unit 기반의 ShuffleNet Unit이 완성되는 것이죠. (c)는 (b)와 동일하지만 stride = 2 인 경우 특징맵의 크기를 맞춰주기 위해 identity path에서 avg pooling을 적용한 것이 차이점입니다.
ShuffleNet Architecture
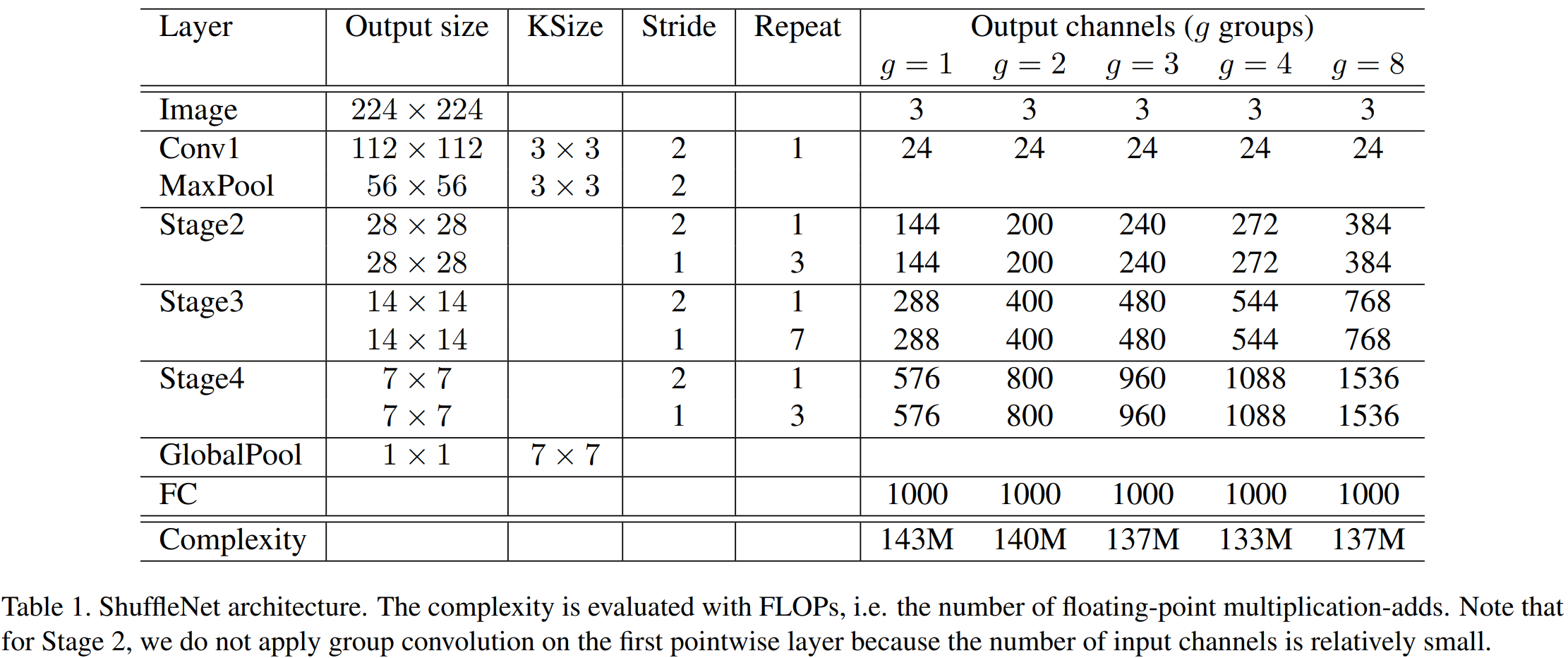
ShuffleNet의 주된 하이퍼파라미터는 그룹의 개수 $g$ 입니다. 표1은 $g$에 따라서 모델을 다르게 구성한 것을 볼 수 있습니다. 여기서 첫번째 합성곱 계층에서 group convolution은 수행하지 않았습니다. 왜냐하면 보통 32개 또는 64개의 채널 개수가 있는 데 이를 group으로 나누기에는 너무 작다는 문제점이 있기 때문이죠.
여기서 추가적인 하이퍼파라미터로 해상도 $s$를 추가합니다. MobileNet에서 ImageNet의 해상도인 224를 기준으로 더 작은 해상도를 사용하여 $s^{2}$만큼의 효율성을 가져왔다는 것을 기억하실 겁니다. 이와 동일한 파라미터이기 때문에 생략하도록 하겠습니다.
따라서, 그룹의 개수 $g$와 해상도를 $s$배만큼 줄인 ShuffleNet을 $\text{ShuffleNet } s \times (g)$로 표기합니다.
Experiment Results
본 논문에서는 ImageNet-1K 데이터셋을 이용하여 실험을 진행합니다. 일다, SOTA와 비교하기 전에 몇 가지 Ablation Study를 시작합니다.
1). Ablation Study
(1). Group Size
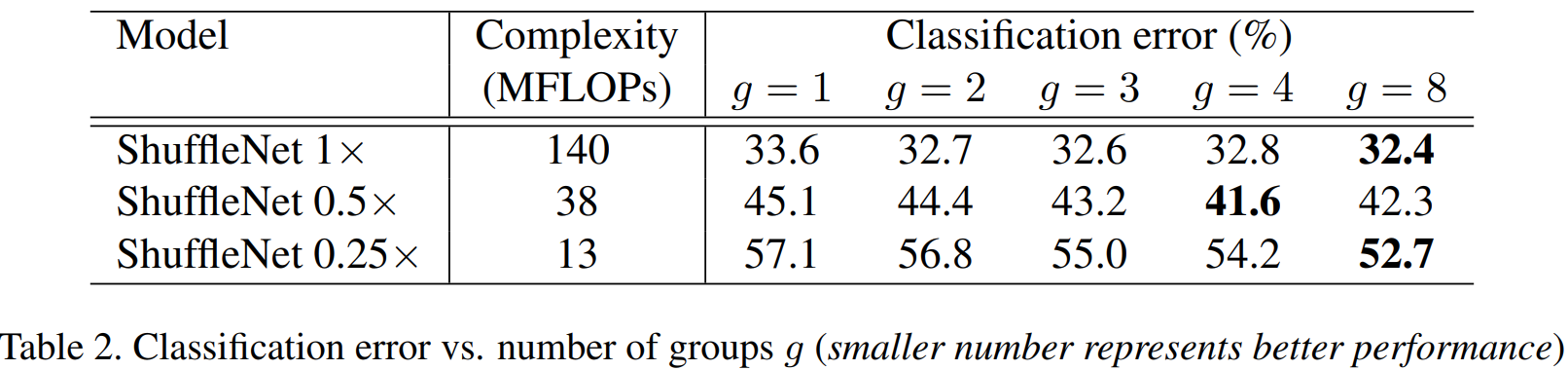
표2는 그룹의 개수 별로 성능을 보여고 있습니다. 보시면 기본적으로 그룹의 개수가 커질수록 성능이 향상되고 잇는 것을 볼 수 있습니다.
(2). w Channel Shuffling vs w/o Channel Shuffling
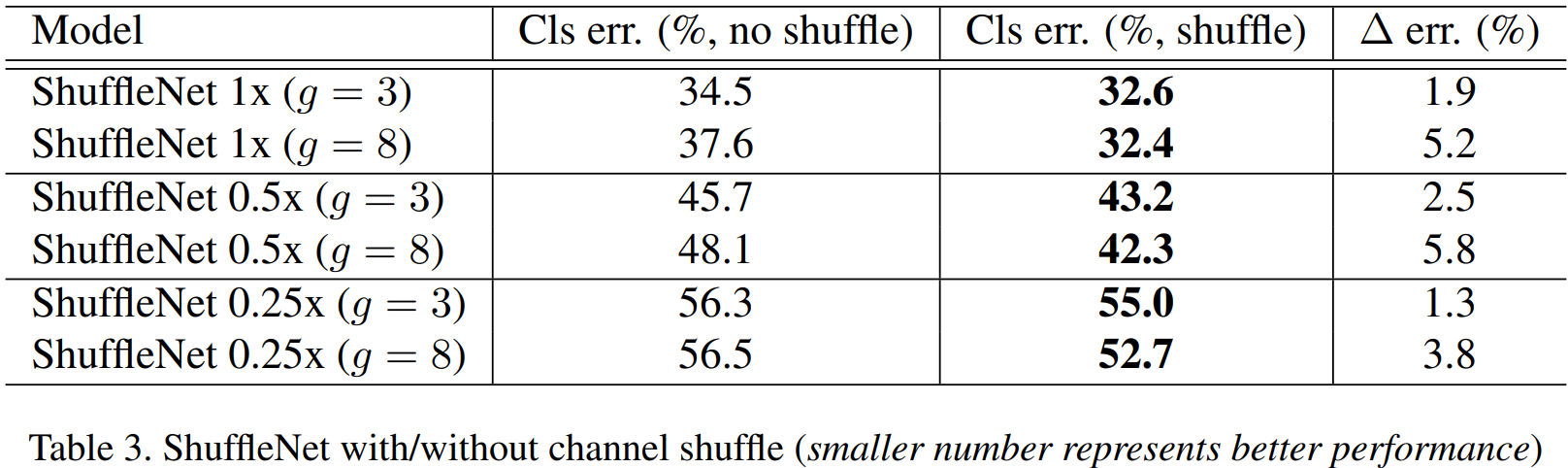
표3은 channel shuffling 연산의 성능 향상 정도를 보여주고 있습니다. 굉장히 단순한 방법으로 높은 마진으로 성능이 향상된 것을 볼 수 있습니다. 특히, 그룹의 개수가 커질수록 그 마진이 높아지는 것을 볼 수 있죠.
2). ImageNet-1K Classification Results

표4는 기존의 모델별로 성능을 보여주고 있습니다. MFLOPs가 낮아질수록 효율적인 모델로 다른 방법들과 달리 ShuffleNet은 성능이 최대한 잘 보존되고 있는 모습입니다.

표5는 MobileNet과 비교를 중점적으로 진행합니다. 보시면 MobileNet보다 훨씬 높은 성능을 가지고 있습니다.
Implementation Code
from collections import OrderedDict
import torch
import torch.nn as nn
import torch.nn.functional as F
from layers import BasicConv
class ChannelShuffle(nn.Module):
def __init__(self, groups):
super(ChannelShuffle, self).__init__()
self.groups = groups
def forward(self, x):
batch_size, channels, height, width = x.size()
channels_per_group = channels // self.groups
# Reshape
x = x.view(batch_size, self.groups, channels_per_group, height, width)
# Transpose
x = torch.transpose(x, 1, 2).contiguous()
# Flatten
x = x.view(batch_size, -1, height, width)
return x
class ShuffleUnit(nn.Module):
def __init__(self, in_channels, out_channels, groups, grouped_conv=True, combine='add'):
super(ShuffleUnit, self).__init__()
self.bottleneck_channels = out_channels // 4
self.combine = combine
if combine == 'add':
stride = (1, 1)
self._combine_func = self._add
elif combine == 'concat':
stride = (2, 2)
self._combine_func = self._concat
out_channels -= in_channels
else:
raise ValueError("Cannot combine tensors with \"{}\"" \
"Only \"add\" and \"concat\" are" \
"supported".format(self.combine))
self.first_1x1_groups = groups if grouped_conv else 1
self.pointwise_group_conv_compress = BasicConv(in_channels, self.bottleneck_channels, kernel_size=(1, 1), stride=(1, 1), padding=(0, 0), groups=groups)
self.channel_shuffle = ChannelShuffle(groups=groups)
self.depthwise_conv = nn.Sequential(
nn.Conv2d(self.bottleneck_channels, self.bottleneck_channels, kernel_size=(3, 3), stride=stride, padding=(1, 1), groups=self.bottleneck_channels),
nn.BatchNorm2d(self.bottleneck_channels))
self.pointwise_group_conv_expand = nn.Sequential(
nn.Conv2d(self.bottleneck_channels, out_channels, kernel_size=(1, 1), stride=(1, 1), padding=(0, 0), groups=groups),
nn.BatchNorm2d(out_channels))
@staticmethod
def _add(x, out):
# residual connection
return x + out
@staticmethod
def _concat(x, out):
# concatenate along channel axis
return torch.cat((x, out), dim=1)
def forward(self, x):
residual = x
if self.combine == 'concat':
residual = F.avg_pool2d(residual, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
out = self.pointwise_group_conv_compress(x)
out = self.channel_shuffle(out)
out = self.depthwise_conv(out)
out = self.pointwise_group_conv_expand(out)
out = self._combine_func(residual, out)
return F.relu(out)
class ShuffleNet(nn.Module):
def __init__(self, num_channels, num_classes, groups=1):
super(ShuffleNet, self).__init__()
self.groups = groups
self.stage_repeats = [3, 7, 3]
if groups == 1:
self.stage_out_channels = [-1, 24, 144, 288, 576]
elif groups == 2:
self.stage_out_channels = [-1, 24, 200, 400, 800]
elif groups == 3:
self.stage_out_channels = [-1, 24, 240, 480, 960]
elif groups == 4:
self.stage_out_channels = [-1, 24, 272, 544, 1088]
elif groups == 8:
self.stage_out_channels = [-1, 24, 384, 768, 1536]
else:
raise ValueError(
"""{} groups is not supported for
1x1 Grouped Convolutions""".format(groups))
# Stage1 Convolution Layer
self.stage1 = nn.Sequential(
nn.Conv2d(num_channels, self.stage_out_channels[1], kernel_size=(3, 3), stride=(2, 2), padding=(1, 1)),
nn.MaxPool2d(kernel_size=(3, 3), stride=(2, 2), padding=(1, 1)))
self.stage2 = self._make_stage(stage_idx=2)
self.stage3 = self._make_stage(stage_idx=3)
self.stage4 = self._make_stage(stage_idx=4)
# Fully-connected classification layer
num_inputs = self.stage_out_channels[-1]
self.fc = nn.Linear(num_inputs, num_classes)
def _make_stage(self, stage_idx):
modules = OrderedDict()
stage_name = "ShuffleUnit_Stage{}".format(stage_idx)
# First ShuffleUnit in the stage
# 1. non-grouped 1x1 convolution (i.e. pointwise convolution)
# is used in Stage 2. Group convolutions used everywhere else.
grouped_conv = stage_idx > 2
# 2. concatenation unit is always used.
first_module = ShuffleUnit(self.stage_out_channels[stage_idx-1], self.stage_out_channels[stage_idx], self.groups, grouped_conv=grouped_conv, combine='concat')
modules[stage_name + '_0'] = first_module
# add more ShuffleUnits depending on pre-defined number of repeats
for i in range(self.stage_repeats[stage_idx - 2]):
name = stage_name + "_{}".format(i + 1)
module = ShuffleUnit(self.stage_out_channels[stage_idx], self.stage_out_channels[stage_idx], self.groups, grouped_conv=True, combine='add')
modules[name] = module
return nn.Sequential(modules)
def forward(self, x):
x = self.stage1(x)
x = self.stage2(x)
x = self.stage3(x)
x = self.stage4(x)
# global average pooling layer
x = F.avg_pool2d(x, x.data.size()[-2:])
# flatten for input to fully-connected layer
x = x.view(x.size(0), -1)
x = self.fc(x)
return F.log_softmax(x, dim=1)
if __name__=='__main__':
model = ShuffleNet(num_channels=3, num_classes=1000, groups=4)
# print(model)
inp = torch.randn((2, 3, 224, 224))
oup = model(inp)
print(oup.shape)
'Paper Review' 카테고리의 다른 글
| Deep Layer Aggregation (CVPR2018) (0) | 2023.06.03 |
|---|---|
| Squeeze-and-Excitation Networks (CVPR2018) (0) | 2023.06.01 |
| Residual Attention Network for Image Classification (CVPR2017) (0) | 2023.05.28 |
| Xception: Deep Learning with Depthwise Separable Convolutions (CVPR2017) (1) | 2023.05.27 |
| PolyNet: A Pursuit of Structural Diversity in Very Deep Networks (CVPR2017) (0) | 2023.05.24 |
