안녕하세요. 지난 포스팅의 [IC2D] Squeeze-and-Excitation Networks (CVPR2018)에서는 어텐션 기반의 블록인 SE Block에 대해서 소개시켜드렸습니다. 오늘은 DenseNet에 이어 다양한 특징 맵을 aggregation하는 두 가지 방법을 제시하는 Deep Layer Aggregation (DLA)에 대해서 소개하도록 하겠습니다.
Deep Layer Aggregation
Visual recognition requires rich representations that span levels from low to high, scales from small to large, and resolutions from fine to coarse. Even with the depth of features in a convolutional network, a layer in isolation is not enough: compounding
arxiv.org
Background
저희가 지금까지 리뷰해왔던 다양한 모델들 (ResNet, Wide ResNet, ResNext, DenseNet, PyramidNet, Inception, ...)은 공통점은 영상 분류 및 객체 탐지를 위해 특징 맵을 어떻게 잘 뽑는 것이 좋을까 입니다. ResNet에서는 기존 특징 맵을 재활용하는 방식을 채택하고 DenseNet은 이전 모든 계층의 특징 맵을 재활용하여 모델의 표현력을 강화시켰죠. 이와 같이 이미 추출된 특징 맵을 재활용하는 방법을 aggregation이라고 부릅니다. 본 논문에서는 이와 같은 방법들을 강화하여 iterative 및 tree 기반의 새로운 aggregation 방법론인 Deep Layer Aggregation을 제안합니다.
DLA는 Iterative Deep Aggregation (IDA)와 Hierarchical Deep Aggregation (HDA)로 두 가지의 형태로 제안되었으며 이 방법들은 모두 객체 인지 및 지역화 능력을 향상시키기 위해 의미론적이고 추상적인 공간 정보를 fusion하는 것이라고 보시면 됩니다. 본 논문에서는 IDA + HDA를 결합하여 새로운 모델을 만들었으며 이 모델은 기존의 모델들보다 적은 파라미터를 가지고 훨씬 높은 성능을 가지는 효율적인 모델입니다.
Deep Layer Aggregation
1). Feature Aggregation

그림1은 기존에 제안된 2가지의 feature aggregation 방법론을 제시하고 있습니다. Dense Connections은 일전에 말씀드린 DenseNet에서 제안된 방법을 하나의 DenseBlock에서 $i$번째 계층의 입력은 첫번째 계층부터 $i - 1$번째 계층의 입력을 모두 가져오는 것입니다. Feature Pyramid Network (FPN)는 아직 소개시켜드리지 않았지만 기존의 multi-scale 기반의 pyramid 형태를 가진 feature들을 활용하여 다양한 크기의 객체를 탐지해야하는 문제에서 자주 활용되고 있는 구조 입니다. 이처럼 이미 특징 맵을 어떻게 하나로 합칠지는 다양한 방식으로 제안되어 왔습니다만, 오늘 소개할 DLA는 DenseNet과 같이 하나의 블록에서만 수행하거나 FPN처럼 shallow한 계층이 shallow한 계층으로만 feature가 합쳐지는 것이 아닌 다양한 스케일에서 다양한 블록 간의 feature를 aggregation하는 것이 목표가 가장 큰 차이점 입니다.
2). Iterative Deep Aggregation (IDA)

위 그림에서 (a)는 VGGNet과 같이 feature aggregtation이 없는 경우, (b)는 FPN과 같이 shallow feature aggregation만 적용한 결과 입니다. (c)가 본 논문에서 첫번째로 제안하는 feature aggregation 방법인 IDA입니다. IDA는 기본적으로 Stage 간의 fusion 방법으로 이는 서로 다른 resolution을 가지는 feature 간의 결합이기 때문에 multi-scale fusion이라고 볼 수 있습니다. IDA에서 각 stage는 같은 resolution을 가지는 계층끼리 엮어놓은 것 입니다. 따라서, stage가 진행될 수록 더 semantic하고 coarser한 feature가 있음을 알 수 있습니다.
각 stage에서 나온결과는 바로 이전 stage의 나온 feature와 결합되거나 이전 aggregation node와 결합되어 다음 aggregation으로 진행됩니다. 그리고 iterative 하게 aggregation이 진행되고 있음을 볼 수 있습니다. 이를 통해, shallow feature가 각 stage의 aggregation node를 거치면서 점점 refine되어간다고 볼 수 있습니다. 이를 수식으로 이해해보면 다음과 같습니다.
$$\begin{align*} I (\mathbf{x}_{1}, \dots, \mathbf{x}_{n}) = \begin{cases} \mathbf{x}_{1} & \text{ if } n = 1 \\ I(N(\mathbf{x}_{1}, \mathbf{x}_{2}), \dots, \mathbf{x}_{n}) & \text{ Otherwise} \end{cases}\end{align*}$$
여기서, $\mathbf{x}_{i}$는 $i$번째 stage에서 나온 feature이고 $N$은 aggregation node 입니다. 수식에서 보시는 것 처럼 재귀적으로 $\mathbf{x}_{1}$부터 $\mathbf{x}_{n}$가 서로 엮어져 있는 것을 볼 수 있습니다. 이를 좀 더 쉽게 이해하기 위해서 그림으로 보도록 하겠습니다.

첫번째 stage에서는 출력인 $\mathbf{x}_{1}$가 두 가지 branch로 나누어져서 각각 입력됩니다. 아래의 branch는 다음 stage로 연결되고 위의 stage는 aggregation node와 연결됩니다.
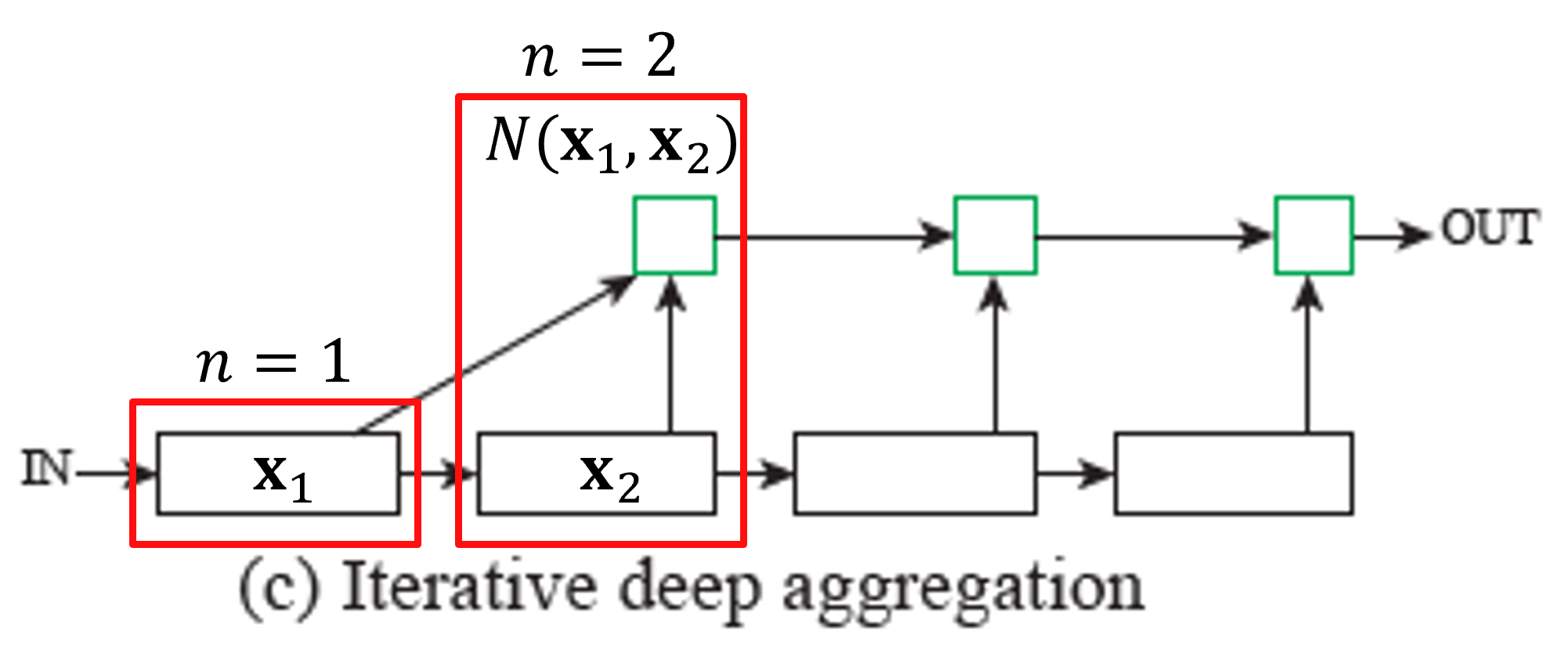
두번째 stage에서도 마찬가지로 출력인 $\mathbf{x}_{2}$가 두 가지 branch로 나누어져서 각각 입력됩니다. 이때, 첫번째 stage와 다른점은 aggregation node에서 $\mathbf{x}_{1}$과 $\mathbf{x}_{2}$가 만난다는 점이죠. 따라서, 위의 처음 본 수식에서는 각 aggregation function $I$를 정의할 때 첫번째 stage면 그냥 $\mathbf{x}_{1}$를 출력하고 두번째 stage면 두 feature $\mathbf{x}_{1}$와 $\mathbf{x}_{2}$를 결합한 $N(\mathbf{x}_{1}, \mathbf{x}_{2})$를 출력하게 되는 것이죠.

세번째 stage에서는 두번째 stage와는 다르게 aggregation function의 출력인 $N(\mathbf{x}_{1}, \mathbf{x}_{2})$를 입력받습니다. 그리고 세번째 stage의 출력 feature와 결합하여 $N(N(\mathbf{x}_{1}, \mathbf{x}_{2}), \mathbf{x}_{3})$를 출력 feature로 내뱉습니다. 이 과정을 계속 반복하는 것이 IDA인 것이죠. IDA는 아주 쉽게 이해할 수 있을 거 같네요.
3). Hierarchical Deep Aggregation (HDA)

이제부터가 문제입니다. HDA 부터는 좀 복잡하기 때문에 차근차근 설명해보도록 하겠습니다. 위 그림은 HDA를 설명하기 위한 몇 가지 트리 구조의 feature aggregation 방법입니다. 여기서 한 가지 꼭 알아두셔야 할 것은 IDA와는 다르게 block 간의 feature aggregation이기 때문에 직사각형이 아닌 정사각형 간의 aggregation이 이루어진다는 점 입니다. 따라서, 스케일을 동일하죠. HDA는 IDA와는 다르게 각 블록의 채널 간의 상관성을 강화시키는 역할이라고 보시면 될 거 같습니다.
먼저, 그림 (d)를 보시도록 하죠. 가장 단순한 트리 구조의 feature aggregation으로 인접한 block들이 좌자식 및 우자식 노드가 되어 상위 부모노드에 연결되고 있습니다. 그리고 그 부모노드는 다시 각각 좌자식 및 우자식 노드가 되어 그 상위의 부모노드로 연결되어 트리구조를 형성하고 있죠.
하지만, 문제점이 한 가지 있습니다. 정작, 부모노드를 통해 인접한 두 노드 간의 좋은 특징을 aggregation을 해놓고 다음 블록으로 전달되지 않기 때문에 sequential한 관계에서는 실질적으로 트리 구조가 사용되고 있지 않다는 점 입니다. 그림 (c)에서는 이러한 문제점을 해결하기 위해서 상위 부모 노드를 다음 sequential block의 입력으로 사용하기 시작합니다.
한 가지 아쉬운 점이 있습니다. 굳이 바로 하위 노드만 입력받은 feature aggregation이 일반적이라고 보기는 어렵습니다. 최종적인 HDA는 그림 (f)와 같이 $i$번째 깊이의 트리 노드는 leaf 노드부터 바로 하위 노드까지 모드 깊이의 노드를 가져오기로 합니다. 이를 수식적으로 나타내면 다음과 같습니다.
$$\begin{align*} T_{n}(\mathbf{x}) = N(R^{n}_{n - 1}(\mathbf{x}), R^{n}_{n - 2}(\mathbf{x}), \dots, R^{n}_{1}(\mathbf{x}), L^{n}_{1}(\mathbf{x}), L^{n}_{2}(\mathbf{x})) \end{align*}$$
여기서 $N$은 IDA와 마찬가지로 aggregation node를 의미합니다. 그리고 $R$과 $L$은 각각 우자식 노드와 좌자식 노드로써 다음과 같이 정의됩니다.
$$L^{n}_{2}(\mathbf{x}) = B(L^{n}_{1}(\mathbf{x}))$$
$$L^{n}_{1}(\mathbf{x}) = B(R^{n}_{1}(\mathbf{x}))$$
$$R^{n}_{m}(\mathbf{x}) = \begin{cases} T_{m}(\mathbf{x}) &\text{ if } m = n = 1 \\ T_{m}(R^{n}_{m + 1}(\mathbf{x})) &\text{ Otherwise} \end{cases}$$
여기서 $B$는 합성곱 블록을 의미합니다. 일단, 저는 위 그림들이랑 수식만 보고 이해하기에는 한계가 있었습니다. 다음 설명을 통해서, 전체적인 HDA를 한번 더 이해해보도록 하겠습니다.
4). Architectural Elements
(1). Aggregation Nodes
일단, Aggregation Node $N$은 입력되는 여러 개의 feature들을 섞고 압축하는 것이 주요 기능입니다. 여기서, IDA와 HDA의 차이점이 나옵니다. IDA는 항상 2개의 입력 feature가 들어오지만 HDA는 트리의 깊이에 따라 다양한 개수의 feature가 입력되기 때문에 이 점을 유의해야합니다.
또한, 태스크에 따라서도 Aggregation Node $N$을 다르게 정의합니다. 만약, 영상 분류가 목적이라면 단순함을 위해 $1 \times 1$ 합성곱 계층에 배치 정규화와 ReLU를 추가하여 feature compression을 주요 목적으로 삼습니다. 반면에 영상 분할이 목적이라면 semantic 정보를 더 추출하기 위해 $3 \times 3$ 합성곱 계층에 배치 정규화와 ReLU를 추가하여 feature combine을 주요 목적으로 삼습니다.
(2). Overall Architecture

그림3은 블록 간의 연결인 HDA와 stage 간의 연결인 IDA를 하나로 합친 DLA입니다. 이제부터 본격적으로 HDA의 동작과정을 설명드리도록 하겠습니다. 기본적으로 제가 수식이 이해가 안됬던 이유가 좌자식 노드 $L$과 우자식 노드 $R$에 붙은 윗첨자와 아랫첨자가 무엇인지 이해가 안됬기 때문이였습니다. 그래서 다양하게 생각해보면서 어떤 의미인지 파악을 해보았는데 그나마 이제부터 제가 설명하는 방식이 제일 이해가 빨랐던 거 같습니다. 혹시, 정확한 의미를 알고 계시다면 댓글을 남겨주시면 감사하겠습니다.
첫번째로 알아야할 것은 HDA를 정의하는 $T_{n}$에서 $n$은 트리의 깊이를 의미합니다. 따라서, leaf 노드에서 바로 위에 있는 상위 노드는 $T_{1}$이 되고 그 다음은 $T_{2}, T_{3}, ...$와 같이 정의됩니다.

그러면 위 그림과 같이 적어볼 수 있겠죠? 이때, 각 노드 $T_{n}(\mathbf{x})$는 $n + 1$개의 자식 노드를 가지게 됩니다. 여기서 노란색 선은 IDA를 의미하기 때문에 제외하고 생각하셔야합니다. 제일 간단한 level 1의 구조를 분석해보도록 하겠습니다.
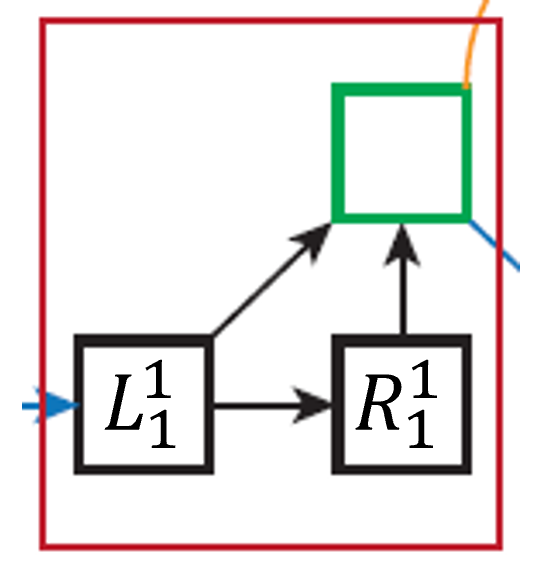
위 그림은 가장 첫번째로 수행되는 HDA를 잘라서 붙인것입니다. Aggregation node를 기준으로 왼쪽 아래는 좌자식 노드 $L^{1}_{1}$, 오른쪽 아래는 우자식 노드 $R^{1}_{1}$과 연결됩니다. 따라서, $T_{n}$의 정의에 의해 다음과 같이 쓸 수 있죠.
$$T_{1}(\mathbf{x}) = N(L^{1}_{1}(\mathbf{x}), L^{1}_{2}(\mathbf{x}))$$
그런데 위 수식에서는 좌자식 노드 $L$밖에 없습니다. 이는 다시 HDA의 정의에서 좌자식 노드를 정의하는 방식을 참고하면 다음과 같이 쓸 수 있습니다.
$$L^{1}_{2}(\mathbf{x}) = B(L^{1}_{1}(\mathbf{x}))$$
$$L^{1}_{1}(\mathbf{x}) = B(R^{1}_{1}(\mathbf{x}))$$
따라서, level 1의 HDA의 출력은 다음과 같이 쓸 수 있습니다.
$$T_{1}(\mathbf{x}) = N(B(R^{1}_{1}(\mathbf{x})), B(L^{1}_{1}(\mathbf{x})))$$

다음은 두번째로 수행되는 HDA입니다. Aggregation node가 2개 존재하고 2개의 깊이로 이루어져있습니다. 그런데 lead 노드 바로 위에 잇는 구조는 첫번재로 수행되는 HDA랑 동일하게 생긴 구조 입니다. 따라서, 가장 왼쪽에서 들어오는 입력은 $T_{1}(\mathbf{x})$가 되죠. 여기서 $T_{n}$의 정의를 보면 $L^{n}_{1}(\mathbf{x})$와 $L^{n}_{2}(\mathbf{x})$는 항상 입력되기 때문에 다음과 같이 쓸 수 있습니다.
$$T_{2}(\mathbf{x}) = N(T_{1}(\mathbf{x}), L^{2}_{1}(\mathbf{x}), L^{2}_{2}(\mathbf{x}))$$
그런데, $T_{1}(\mathbf{x})$는 우자식 노드 $R^{2}_{1}(\mathbf{x})$의 정의에 의해 동일하므로 다음과 같이 쓸 수 있습니다.
$$T_{2}(\mathbf{x}) = N(R^{2}_{1}(\mathbf{x}), B(R^{2}_{1}(\mathbf{x})), B(L^{2}_{1}(\mathbf{x})))$$

마지막으로 최대 깊이인 level 3 입니다. 이는 정의를 이용해서 써보면 위와 같이 이전 트리의 결과 + 연결된 leaf 노드의 좌우자식 노드를 aggregation하는 것임을 볼 수 있습니다.
(3). DLA + Residual Connections
위 그림들에서는 나오지 않았지만 DLA에서는 aggregation node에 Residual Connection을 추가한 뒤 학습했다고 합니다. 따라서, 위에서 언급한 aggregation node의 정의와 합치면 다음과 같이 쓸 수 있죠.
- w/o Residual Connection : $N(\mathbf{x}_{1}, \dots, \mathbf{x}_{n}) = \sigma (\text{BN} (\sum_{i} W_{i}\mathbf{x}_{i} + b_{i}))$
- w Residual Connection : $N(\mathbf{x}_{1}, \dots, \mathbf{x}_{n}) = \sigma (\text{BN} (\sum_{i} W_{i}\mathbf{x}_{i} + b_{i}) + \mathbf{x}_{n})$
Deep Layer Aggregation Architecture

여기서, C는 기존의 DLA모델보다 연산량을 적게 잡아서 만든 모델로 채널의 개수가 적은 모델입니다. X는 group convolution을 통해 만든 DLA를 의미합니다.
Experiment Results
본 논문에서는 ImageNet-1K 데이터셋을 이용해서 영상 분류 실험 및 CityScape 데이터셋을 이용해서 영상 분할 실험을 진행합니다. 영상 분류 실험의 실험 결과만 언급하도록 하겠습니다.
1). ImageNet-1K Classification Results

기존에 feature aggregation을 수행하는 모델들보다 보다 나은 성능을 보여주고 있습니다.
Implementation Code
import torch
import torch.nn as nn
import torch.nn.functional as F
from layers import BasicConv
class BasicBlock(nn.Module) :
"""Basic Block for resnet 18 and resnet 34
"""
#BasicBlock and BottleNeck block
#have different output size
#we use class attribute expansion
#to distinct
expansion = 1
def __init__(self, in_channels, out_channels, stride=1, dilation=1) :
super(BasicBlock, self).__init__()
# residual function
self.residual_function = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=(3, 3), stride=(stride, stride), padding=(dilation, dilation), dilation=(dilation, dilation), bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels * BasicBlock.expansion, kernel_size=(3, 3), padding=(dilation, dilation), dilation=(dilation, dilation), bias=False),
nn.BatchNorm2d(out_channels * BasicBlock.expansion)
)
def forward(self, x, residual=None):
if residual is None: residual = x
return nn.ReLU(inplace=True)(self.residual_function(x) + residual)
class BottleneckBlock(nn.Module):
expansion = 2
def __init__(self, in_channels, out_channels, stride=1, dilation=1):
super(BottleneckBlock, self).__init__()
bottle_planes = out_channels // BottleneckBlock.expansion
self.residual_function = nn.Sequential(
nn.Conv2d(in_channels, bottle_planes, kernel_size=1, bias=False),
nn.BatchNorm2d(bottle_planes), nn.ReLU(inplace=True),
nn.Conv2d(bottle_planes, bottle_planes, stride=stride, kernel_size=3, padding=dilation, dilation=dilation, bias=False),
nn.BatchNorm2d(bottle_planes), nn.ReLU(inplace=True),
nn.Conv2d(bottle_planes, out_channels, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels))
def forward(self, x, residual=None):
if residual is None: residual = x
return nn.ReLU(inplace=True)(self.residual_function(x) + residual)
class BottleneckXBlock(nn.Module):
expansion=2
cardinality = 32
def __init__(self, in_channels, out_channels, stride=1, dilation=1):
super(BottleneckXBlock, self).__init__()
bottle_planes = in_channels * BottleneckXBlock.cardinality // 32
self.residual_function = nn.Sequential(
nn.Conv2d(in_channels, bottle_planes, kernel_size=1, bias=False),
nn.BatchNorm2d(bottle_planes), nn.ReLU(inplace=True),
nn.Conv2d(bottle_planes, bottle_planes, stride=stride, kernel_size=3, padding=dilation, dilation=dilation, bias=False, groups=BottleneckXBlock.cardinality),
nn.BatchNorm2d(bottle_planes), nn.ReLU(inplace=True),
nn.Conv2d(bottle_planes, out_channels, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels))
def forward(self, x, residual=None):
if residual is None: residual = x
return nn.ReLU(inplace=True)(self.residual_function(x) + residual)
class Root(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, residual):
super(Root, self).__init__()
self.conv = BasicConv(in_channels, out_channels, kernel_size=kernel_size, stride=(1, 1), padding=(kernel_size - 1) // 2, bias=False, relu=False)
self.residual = residual
def forward(self, *x):
children = x
x = self.conv(torch.cat(x, dim=1))
if self.residual:
x += children[0]
x = F.relu(x)
return x
class Tree(nn.Module):
def __init__(self, block, in_channels, out_channels, max_level, stride=1, dilation=1,
root_dim=0, root_kernel_size=1, root_residual=False, level_root=False):
super(Tree, self).__init__()
if root_dim == 0: root_dim = 2 * out_channels
if level_root: root_dim += in_channels
if max_level == 1:
self.tree1 = block(in_channels, out_channels, stride=stride, dilation=dilation)
self.tree2 = block(out_channels, out_channels, stride=1, dilation=dilation)
self.root = Root(root_dim, out_channels, root_kernel_size, root_residual)
else:
self.tree1 = Tree(block, in_channels, out_channels, max_level - 1, stride=stride, dilation=dilation,
root_dim=0, root_kernel_size=root_kernel_size, root_residual=root_residual)
self.tree2 = Tree(block, out_channels, out_channels, max_level - 1, dilation=dilation,
root_dim=root_dim + out_channels, root_kernel_size=root_kernel_size, root_residual=root_residual)
self.level_root = level_root
self.root_dim = root_dim
self.downsample = None
self.project = None
self.max_level = max_level
if stride > 1: self.downsample = nn.MaxPool2d(kernel_size=stride, stride=stride)
if in_channels != out_channels: self.project = BasicConv(in_channels, out_channels, kernel_size=1, stride=1, padding=0, bias=False, relu=False)
def forward(self, x, residual=False, children=None):
children = children if children else []
bottom = self.downsample(x) if self.downsample else x
residual = self.project(bottom) if self.project else bottom
if self.level_root: children.append(bottom)
x1 = self.tree1(x, residual)
if self.max_level == 1:
x2 = self.tree2(x1)
x = self.root(x2, x1, *children)
else:
children.append(x1)
x = self.tree2(x1, children=children)
return x
class DLA(nn.Module):
def __init__(self, block, max_level_list, channel_list, num_channels=3, num_classes=1000,
residual_root=False,
pool_size=7):
"""
:param max_level_list: maximum depth of tree
:param channel_list: number of channel per each stage
:param num_channels: number of input image channel
:param num_classes: number of class
"""
super(DLA, self).__init__()
self.num_stage = len(channel_list)
self.conv1 = BasicConv(num_channels, channel_list[0], kernel_size=(7, 7), stride=(1, 1), padding=(3, 3), bias=False)
self.level0 = self._make_conv_level(channel_list[0], channel_list[0], max_level=max_level_list[0], kernel_size=(3, 3), stride=(1, 1))
self.level1 = self._make_conv_level(channel_list[0], channel_list[1], max_level=max_level_list[1], kernel_size=(3, 3), stride=(2, 2))
self.level2 = Tree(block, channel_list[1], channel_list[2], max_level=max_level_list[2], stride=2, level_root=False, root_residual=residual_root)
self.level3 = Tree(block, channel_list[2], channel_list[3], max_level=max_level_list[3], stride=2, level_root=True, root_residual=residual_root)
self.level4 = Tree(block, channel_list[3], channel_list[4], max_level=max_level_list[4], stride=2, level_root=True, root_residual=residual_root)
self.level5 = Tree(block, channel_list[4], channel_list[5], max_level=max_level_list[5], stride=2, level_root=True, root_residual=residual_root)
self.avgpool = nn.AvgPool2d(pool_size)
self.fc = nn.Conv2d(channel_list[5], num_classes, kernel_size=1, stride=1, padding=0, bias=True)
def _make_conv_level(self, in_channels, out_channels, max_level, kernel_size, stride=1, dilation=1):
modules = []
for idx in range(max_level):
modules.append(BasicConv(in_channels, out_channels,
kernel_size=kernel_size,
stride=(1, 1) if idx else stride,
padding=dilation,
dilation=dilation,
bias=False))
in_channels = out_channels
return nn.Sequential(*modules)
def forward(self, x):
x = self.conv1(x)
for idx in range(6):
x = getattr(self, 'level{}'.format(idx))(x)
print(x.shape)
x = self.avgpool(x)
x = self.fc(x)
x = x.view(x.size(0), -1)
return x
def dla34(num_channels=3, num_classes=1000):
model = DLA(BasicBlock,
[1, 1, 1, 2, 2, 1],
[16, 32, 64, 128, 256, 512],
num_channels=num_channels, num_classes=num_classes)
return model
def dla46c(num_channels=3, num_classes=1000):
BottleneckBlock.expansion = 2
model = DLA(BottleneckBlock,
[1, 1, 1, 2, 2, 1],
[16, 32, 64, 64, 128, 256],
num_channels=num_channels, num_classes=num_classes)
return model
def dla46cx(num_channels=3, num_classes=1000):
BottleneckXBlock.expansion = 2
model = DLA(BottleneckXBlock,
[1, 1, 1, 2, 2, 1],
[16, 32, 64, 64, 128, 256],
num_channels=num_channels, num_classes=num_classes)
return model
if __name__=='__main__':
model = dla46cx()
inp = torch.randn(2, 3, 256, 256)
oup = model(inp)
print(oup.shape)
