안녕하세요. 지난 포스팅의 [IC2D] Aggregated Residual Transformations for Deep Neural Networks (CVPR2017)에서는 깊이(depth)나 너비 (width)보다 cardinality의 중요성을 강조하는 ResNext를 제안하였습니다. ResNet과 유사한 복잡도를 가지지만 성능 향상은 꽤 높은 편이였죠. 오늘은 계층간의 연결성 (connection)을 강조한 DenseNet에 대해서 소개해드리도록 하겠습니다.
Densely Connected Convolutional Networks
Recent work has shown that convolutional networks can be substantially deeper, more accurate, and efficient to train if they contain shorter connections between layers close to the input and those close to the output. In this paper, we embrace this observa
arxiv.org
Background
대부분의 모델의 기반이 되는 ResNet에서는 skip connection 구조를 적용하여 forward 과정에서 소실되는 특징과 backward 과정에서 소실되는 기울기를 안정적으로 전달함으로써 성능을 향상시키게 됩니다. 이를 통해, 더욱 깊은 네트워크에서도 안정적으로 학습할 수 있게 되었죠. 하지만, 깊게 만들게 되면 여전히 수많은 계층을 지나게 되면서 얕은 계층의 정보가 깊은 계층으로 전달되지 못하는 경우가 있습니다.
본 논문에서는 이를 방지하기 위해 $L$번째 계층의 입력 특징맵은 첫번째 계층부터 $L - 1$번째 계층의 출력 특징맵까지의 concat된 특징 맵이 됩니다. 이와 같은 구조의 모델을 Dense Convolutional Network (DenseNet)이라고 정의하였죠. 이러한 효과는 불필요하게 중복된 특징 맵을 학습할 필요없이 더 적은 파라미터로 좋은 성능을 이끌어낼 수 있다고 언급합니다.
DenseNets

그림1은 DenseNet의 1개의 block에 대한 블록 다이어그램을 보여주고 있습니다. 본 논문에서는 비선형변환 $H_{l}(\cdot)$을 구현하기 위해 배치 정규화 (batch normalization), Recified Linear Unit (ReLU), 풀링 그리고 합성곱 연산을 연달하게 사용하였습니다. 여기서 $\mathbf{x}_{l}$은 $l$번째 계층의 출력 특징 맵으로 표기합니다.
1). ResNets
아무래도 DenseNet은 ResNet에서 영감을 받았기 때문에 간단한 설명을 해야할 거 같습니다. ResNet에서는 $l$번째 계층에서 $l + 1$ 번째 계층의 출력으로의 skip connection을 적용하여 다음과 같은 연산을 수행하였습니다.
$$\mathbf{x}_{l} = H_{l}(\mathbf{x}_{l - 1}) + \mathbf{x}_{l - 1}$$
이를 통해, Gradient vanishing problem을 방지하여 학습의 효율을 향상시킵니다. 하지만, ideneity function과 $H_{l}$의 출력이 원소별 합으로 합쳐지기 때문에 이는 모델의 데이터 흐름에 방해가 될 수 있습니다.
2). Dense Connectivity
DenseNet은 이러한 단점을 해결하기 위해 원소별 합이 아닌 concat 연산을 사용하였습니다. 그리고, 바로 직전 계층의 출력 특징맵만 concat하는 것이 아니라 이전의 모든 계층의 출력 특징 맵을 concat하여 정보를 취합합니다. 따라서, DenseNet에서 $l$번째 계층의 입력과 출력은 다음과 같이 정의됩니다.
$$\mathbf{x}_{l} = H_{l}([\mathbf{x}_{0}, \mathbf{x}_{1}, \dots, \mathbf{x}_{l - 1}])$$
여기서, $[\mathbf{x}_{0}, \mathbf{x}_{1}, \dots, \mathbf{x}_{l - 1}]$이 0번째 계층부터 $l - 1$번째 계층까지의 출력 특징맵의 concat 연산을 의미합니다. 이와 같이 연결이 빽빽하게 (densely)하게 형성되었기 때문에 Dense Convolutional Network라고 정의한 것이죠.
3). Composite function
DenseNet은 PreAct ResNet에 영감을 받아 배치 정규화-ReLU-합성곱 순서의 연산을 수행합니다.
4). Pooling Layers

그림2는 3개의 DenseBlock을 가지는 DenseNet의 구조입니다. 일반적으로 합성곱 신경망에서는 특징 맵의 해상도를 줄이기 위한풀링 계층이 존재합니다. 그림2에서는 DenseBlock 사이에 존재하죠. 본 논문에서는 이를 효율적으로 수행하기 위해 Transition Layer라는 것을 추가합니다. 사실 이름만 거창하지 별거 없습니다. 그냥 $1 \times 1$ 합성곱 계층에 $2 \times 2$ 평균 풀링 계층을 연달아서 사용한 것이죠.
5). Growth rate
DenseBlock 내의 비선형변환 $H_{l}$은 모두 $k$개의 특징 맵을 출력한다고 가정하겠습니다. 그러면 한 개의 DenseBlock에서 총 $l$개의 계층이 있다고 가정하면 해당 DenseBlock에서 $l$번째 계층의 입력 특징맵의 채널 개수는 $k_{0} + k (l - 1)$입니다. 잘 보시면 이는 초항이 $k_{0}$이고 공차가 $k$인 등차수열의 모습입니다. $k_{0}$은 이전 DenseBlock의 출력 특징맵의 채널개수이므로 조절불가입니다. 하지만, $k$는 저희가 조절하여 특징맵의 차원을 조절할 수 있습니다. 만약, $k$가 너무 크면 특징맵의 차원이 굉장히 커지기 때문에 계산량이 너무 커집니다. 이를 방지하기 위해 등차수열의 형태로 한 개의 DenseBlock 내 존재하는 계층들이 모두 동일한 크기의 출력 특징맵을 가지도록 만드는 것이죠. 이를 growth rate라고 정의하고 DenseNet의 하이퍼파라미터가 됩니다.
6). Bottleneck layers
growth rate $k$를 이용하여 연산량을 조절한다고 하더라도 여전히 ResNet보다는 연산량이 훨씬 클 수밖에 없습니다. DenseNet은 이를 해결하기 위해 기존의 ResNet에서 사용했던 Bottleneck block을 활용합니다. 기존의 ResNet50과 ResNet101과 같이 깊은 모델에서는 연산량이 매우 커지기 때문에 이를 해결하기 위해 $1 \times 1$ 합성곱 계층으로 특징 맵의 크기를 조절하는 것을 볼 수 있었습니다. DenseNet에서도 이러한 구조를 활용하는 것이죠. 따라서, DenseNet + Bottleneck을 이용한 경우 DenseNet-B라고 표기하도록 하겠습니다. 그러면 DenseNet-B의 $l$번째 계층 $H_{l}$의 구성은 배치 정규화-ReLU-$1 \times 1$ 합성곱-배치 정규화-ReLU-$3 \times 3$ 합성곱이 됩니다. 여기서, $1 \times 1$ 합성곱은 growth rate의 4배인 $4k$만큼의 특징맵을 만들게 됩니다. 이는 하나의 하이퍼파라미터로 실험적으로 검증한 듯 합니다.
7). Compression
마지막으로 DenseNet의 Compantness를 향상시키기 위해 transition layer의 특징맵의 개수를 추가적으로 감소시킵니다. 각 DenseBlock인 $m$개의 특징 맵을 출력한다고 가정하면 compression factor $\theta \in (0, 1]$을 이용하여 transition layer에서는 $\lfloor \theta m \rfloor$만큼의 특징 맵으을 출력하게 됩니다. 만약, $\theta = 1$이라면 압축되지 않고 그대로 사용하는 것이기 때문에 연산량은 유지됩니다. 본 논문에서는 $\theta = 0.5$로 고정하여 실험을 진행하였으며 이와 같이 compression을 적용한 DenseNet을 DenseNet-C로 표기합니다. 이때, 6)에서 설명한 Bottleneck layer와 함께 적용하여 DenseNet-BC를 이용해서 실험을 진행하였습니다.
DenseNet Architecture

표1은 DenseNet의 다양한 변형 모델을 보여주고 있습니다. 본 논문에서는 총 4가지의 변형 모델을 구성하였으며 growth rate $k =32, \theta = 0.5$로 고정하였습니다.
Experiment Results
본 논문에서는 CIFAR10, CIFAR100, SVHN, ImageNet 데이터셋을 이용한 영상 분류 실험을 진행하였습니다.
1). Classification Results in CIFAR and SVHN

제일 먼저 CIFAR와 SVHN에서의 성능 비교를 해보도록 하겠습니다. 여기서 '+'는 일반적으로 사용하는 데이터 증강 (translation, flipping)을 적용하고 실험한 것을 의미합니다. 저희가 지금까지 보았던 ResNet, ResNet with Stochastic Depth, WRN, PreAct ResNet과 성능을 비교하였으며 모든 경우에서 DenseNet이 훨씬 더 좋은 성능을 보이고 있습니다.
2). Classification Results on ImageNet
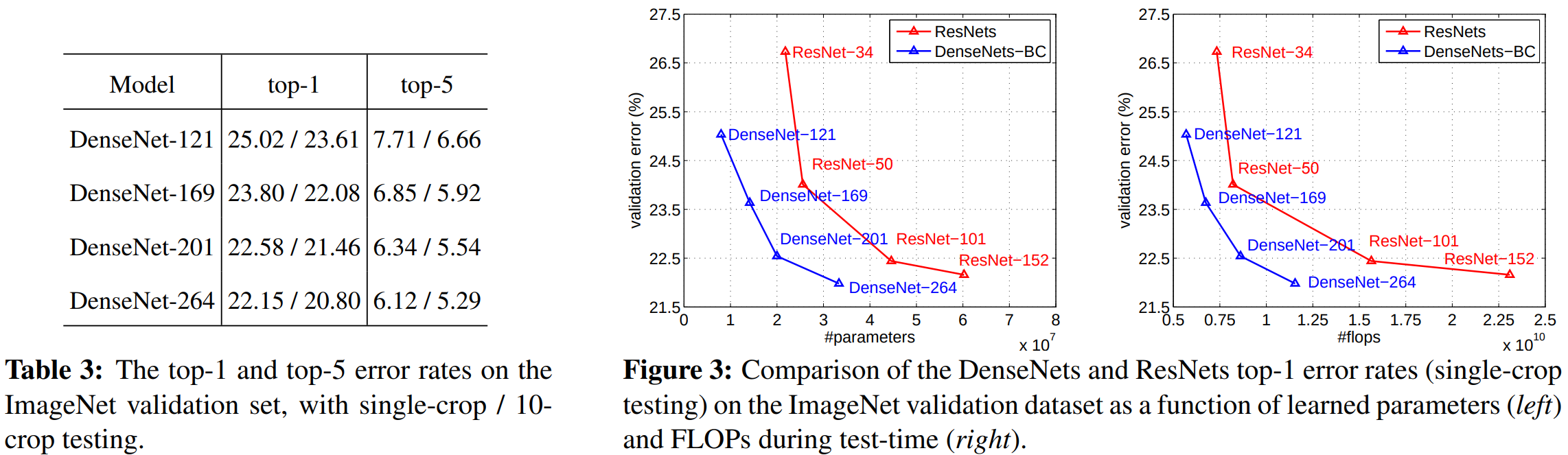
이번에는 ImageNet 데이터셋에서 성능 비교를 해보도록 하겠습니다. 저는 그림3이 중요하다고 생각하고 있습니다. 모델의 파라미터와 연산량에 따른 성능 변화를 보여주고 있습니다. ResNet이랑만 비교를 하고는 있지만 그래도 ResNet보다 훨씬 적은 파라미터와 연산량만으로도 훨씬 좋은 성능을 보이고 있습니다.
Implementation Code
"""dense net in pytorch
[1] Gao Huang, Zhuang Liu, Laurens van der Maaten, Kilian Q. Weinberger.
Densely Connected Convolutional Networks
https://arxiv.org/abs/1608.06993v5
"""
import torch
import torch.nn as nn
#"""Bottleneck layers. Although each layer only produces k
#output feature-maps, it typically has many more inputs. It
#has been noted in [37, 11] that a 1×1 convolution can be in-
#troduced as bottleneck layer before each 3×3 convolution
#to reduce the number of input feature-maps, and thus to
#improve computational efficiency."""
class Bottleneck(nn.Module):
def __init__(self, in_channels, growth_rate):
super().__init__()
#"""In our experiments, we let each 1×1 convolution
#produce 4k feature-maps."""
inner_channel = 4 * growth_rate
#"""We find this design especially effective for DenseNet and
#we refer to our network with such a bottleneck layer, i.e.,
#to the BN-ReLU-Conv(1×1)-BN-ReLU-Conv(3×3) version of H ` ,
#as DenseNet-B."""
self.bottle_neck = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.ReLU(inplace=True),
nn.Conv2d(in_channels, inner_channel, kernel_size=1, bias=False),
nn.BatchNorm2d(inner_channel),
nn.ReLU(inplace=True),
nn.Conv2d(inner_channel, growth_rate, kernel_size=3, padding=1, bias=False)
)
def forward(self, x):
return torch.cat([x, self.bottle_neck(x)], 1)
#"""We refer to layers between blocks as transition
#layers, which do convolution and pooling."""
class Transition(nn.Module):
def __init__(self, in_channels, out_channels):
super().__init__()
#"""The transition layers used in our experiments
#consist of a batch normalization layer and an 1×1
#convolutional layer followed by a 2×2 average pooling
#layer""".
self.down_sample = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.Conv2d(in_channels, out_channels, 1, bias=False),
nn.AvgPool2d(2, stride=2)
)
def forward(self, x):
return self.down_sample(x)
#DesneNet-BC
#B stands for bottleneck layer(BN-RELU-CONV(1x1)-BN-RELU-CONV(3x3))
#C stands for compression factor(0<=theta<=1)
class DenseNet(nn.Module):
def __init__(self, block, nblocks, num_classes, num_channels, growth_rate=12, reduction=0.5):
super().__init__()
self.growth_rate = growth_rate
#"""Before entering the first dense block, a convolution
#with 16 (or twice the growth rate for DenseNet-BC)
#output channels is performed on the input images."""
inner_channels = 2 * growth_rate
#For convolutional layers with kernel size 3×3, each
#side of the inputs is zero-padded by one pixel to keep
#the feature-map size fixed.
self.conv1 = nn.Conv2d(num_channels, inner_channels, kernel_size=3, padding=1, bias=False)
self.features = nn.Sequential()
for index in range(len(nblocks) - 1):
self.features.add_module("dense_block_layer_{}".format(index), self._make_dense_layers(block, inner_channels, nblocks[index]))
inner_channels += growth_rate * nblocks[index]
#"""If a dense block contains m feature-maps, we let the
#following transition layer generate θm output feature-
#maps, where 0 < θ ≤ 1 is referred to as the compression
#fac-tor.
out_channels = int(reduction * inner_channels) # int() will automatic floor the value
self.features.add_module("transition_layer_{}".format(index), Transition(inner_channels, out_channels))
inner_channels = out_channels
self.features.add_module("dense_block{}".format(len(nblocks) - 1), self._make_dense_layers(block, inner_channels, nblocks[len(nblocks)-1]))
inner_channels += growth_rate * nblocks[len(nblocks) - 1]
self.features.add_module('bn', nn.BatchNorm2d(inner_channels))
self.features.add_module('relu', nn.ReLU(inplace=True))
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.linear = nn.Linear(inner_channels, num_classes)
def forward(self, x):
output = self.conv1(x)
output = self.features(output)
output = self.avgpool(output)
output = output.view(output.size()[0], -1)
output = self.linear(output)
return output
def _make_dense_layers(self, block, in_channels, nblocks):
dense_block = nn.Sequential()
for index in range(nblocks):
dense_block.add_module('bottle_neck_layer_{}'.format(index), block(in_channels, self.growth_rate))
in_channels += self.growth_rate
return dense_block
def densenet121(num_classes, num_channels):
return DenseNet(Bottleneck, [6,12,24,16], num_classes, num_channels, growth_rate=32)
def densenet169(num_classes, num_channels):
return DenseNet(Bottleneck, [6,12,32,32], num_classes, num_channels, growth_rate=32)
def densenet201(num_classes, num_channels):
return DenseNet(Bottleneck, [6,12,48,32], num_classes, num_channels, growth_rate=32)
def densenet161(num_classes, num_channels):
return DenseNet(Bottleneck, [6,12,36,24], num_classes, num_channels, growth_rate=48)
