안녕하세요. 지난 포스팅의 [IC2D] Pelee: A Real-Time Object Detection System on Mobile Devices (NIPS2018)에서는 Group Convolution의 구현이 비효율적으로 구현되어 있다는 것을 지적하며 Group Convolution없이 모델의 효율성을 향상시킬 수 있는 모델인 PeleeNet에 대해서 소개시켜드렸습니다. 오늘은 기존의 ShuffleNet의 다음 버전인 ShuffleNet V2에 대해서 소개시켜드리도록 하겠습니다.
ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design
Currently, the neural network architecture design is mostly guided by the \emph{indirect} metric of computation complexity, i.e., FLOPs. However, the \emph{direct} metric, e.g., speed, also depends on the other factors such as memory access cost and platfo
arxiv.org
Background
지금까지 효율성을 증가시키기 위한 많은 논문들에서 사용하는 측정 방식은 FLOPs와 모델의 파라미터 개수 였습니다. 여기서, FLOPs는 FLoat-point OPerations의 준말로 모델이 초당 계산할 수 있는 부동 소수점 연산의 횟수를 의미하죠. 본 논문에서는 이에 대해 반박합니다. FLOPs 만이 속도를 판별할 수 있는 유일한 측정 방식이냐는 것이죠.

그림1을 보시면 두 개의 플랫폼 (GPU, ARM)에서 성능 및 FLOPs에 따른 속도 변화를 다양한 모델별로 보여주고 있습니다. 일반적으로 저희는 FLOPs가 높으면 그만큼 속도가 빨라질 것이라고 생각합니다. 하지만, 현실은 그 반대이죠. 이러한 결과는 FLOPs 말고도 다른 요소가 모델의 실제 속도에 영향을 끼친다는 것을 알 수 있습니다. 따라서, FLOPs만 따라서 모델의 효율성을 설계하면 오히려 실제 속도를 떨어질 수도 있다는 것을 의미합니다!!
본 논문에서는 이와 같이 모델의 속도에 직접적으로 상관성이 없는 metric을 indirect metric이라고 부르기로 합니다. 반면에, 직접적인 영향이 큰 metric을 direct metric이라고 부르죠. 대표적으로 MAC (Memory Access Cost)라고 부르는 것으로 data I/O 과정에서 많은 연산이 포함되는 metric 입니다. 다른 요소는 degree of parallelism으로 모델의 효율적인 병렬화는 곧 속도를 상승시키는 것이라고 하네요.

마지막으로 모델의 속도는 구현된 플랫폼에 따라서도 달라진다고 합니다. 그림2에서는 GPU와 ARM에서 ShuffleNet과 MobileNet의 연산량을 분석해보았을 때 플랫폼 별로 차지되고 있는 연산의 비율이 크게 차이가 나는 것을 볼 수 있습니다.
본 논문에서는 이러한 배경에 맞춰 효율적인 모델을 설계할 수 있는 4가지 가이드라인을 제시합니다. 이를 통해, 설계한 모델이 바로 ShuffleNet V2인 것이죠.
2. Practical Guidelines for Efficient Network Design
본 논문에서는 크게 2가지 플랫폿인 GPU (NVIDIA GeForce 1080Ti)와 ARM (Qualcomm Snapdragon 810)에서 성능을 측정합니다. 그리고 효율적인 모델을 위한 가이드라인을 설계하기 위한 기초적인 실험으로 ShuffleNet V1과 MobileNet V2를 이용하기로 합니다. 이 두 모델 모두 ImageNet에서 굉장히 높은 효율을 가지는 모델이기 때문이죠. 두 모델을 공부하시면 아시겠지만 각 모델의 핵심은 Group Convolution과 Depthwise Separable Convolution입니다. 그림2에서는 두 모델의 플랫폼 별 각 연산에 대한 비용을 보여주고 있습니다. 보시면 FLOPs에 직접적으로 관여하는 convolution은 GPU에서 50% 정도, ARM에서는 90% 정도 차지하고 있죠. 따라서, FLOPs보다는 MAC에 집중하여 새로운 가이드라인을 세우기로 합니다.
G1). Equal channel width minimizes MAC
현재 많은 모델들이 Depthwise Separable Convolution을 활용하고 있습니다. 대표적으로 XCeption, ResNext, MobileNet V1, MobileNet V2, CondenseNet이 있었죠. 그 중에서도 pointwise convolution인 $1 \times 1$ 합성곱 연산이 가장 많은 연산량을 차지하고 있으며 FLOPs는 $B = hwc_{1}c_{2}$로 계산됩니다. 식을 보시면 어차피 $h$와 $w$는 고정값이고 $c_{1}$과 $c_{2}$가 변하는 값이므로 둘 사이의 비율을 조정하며 실험을 해보기로 합니다.

https://arxiv.org/abs/1807.11164
실험결과는 입력 및 출력 채널의 크기가 동일할 때인 $c_{1} : c_{2} = 1 : 1$일 때 GPU와 ARM에서 가장 속도가 빠른 것을 알 수 있습니다. 사실 이러한 결과는 수식적으로도 증명해볼 수 있습니다. 일반적으로 $\text{MAC} = hw (c_{1} + c_{2}) + c_{1}c_{2}$로 계산할 수 있다고 합니다. 이는 평균값 정리로 인해 다음 부등식을 얻을 수 있습니다.
$$\text{MAC} \ge 2\sqrt{hwB} + \frac{B}{hw}$$
이때, MAC이 최소가 되기 위해서는 $c_{1} = c_{2}$인 경우이므로 입력 및 출력 채널의 개수가 동일해야함을 알 수 있습니다.
G2). Excessive group convolution increase MAC
Group Convolution은 ShuffleNet V1에서 적극적으로 활용하여 연산량을 줄이는 데 아주 중요한 역할을 하였습니다. 하지만, 이는 FLOPs 기준으로 MAC은 오히려 증가하는 현상이 발생합니다. 일반적으로 $g$개의 그룹을 가지는 Group Convolution에서 MAC은 다음과 같이 계산됩니다.
$$\begin{align*} \text{MAC} &= hw (c_{1} + c_{2}) + \frac{c_{1}c_{2}}{g} \\ &= hwc_{1} + \frac{Bg}{c_{1}} + \frac{B}{hw} \end{align*}$$
여기서, $B = \frac{hwc_{1}c_{2}}{g}$로 $g$개의 그룹을 가지는 경우의 FLOPs로 정의됩니다. FLOPs와 MAC을 비교해보면 FLOPs는 $g$가 분모에 있기 때문에 증가할 수록 FLOPs는 감소하게 됩니다. 하지만, MAC는 분자에 붙어있기 때문에 증가하게 되죠.
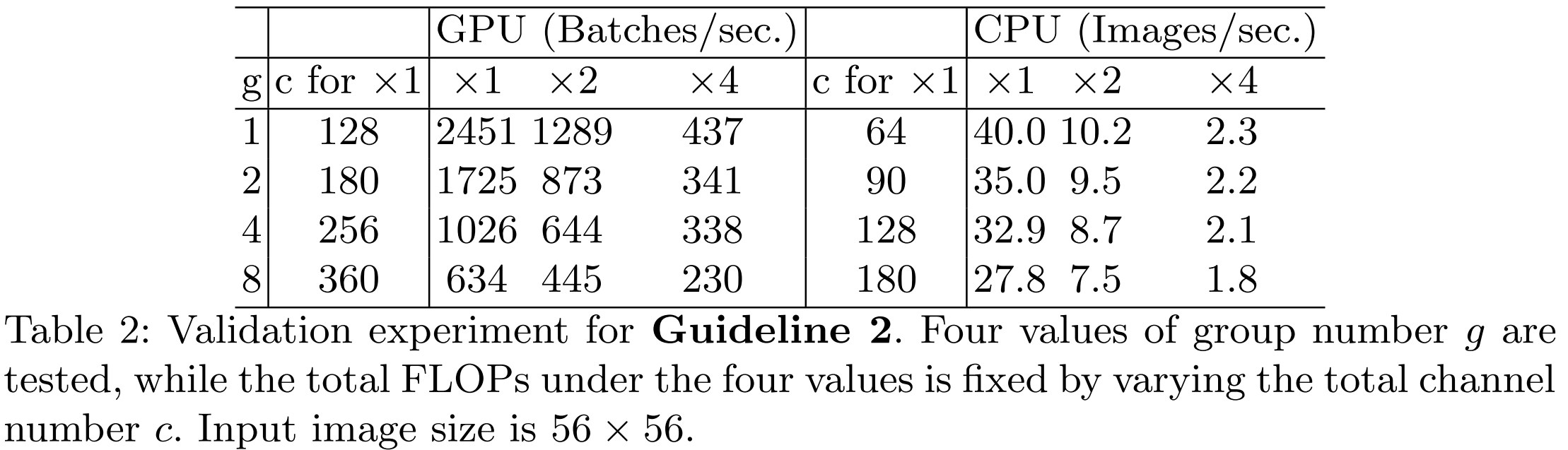
표2는 위 결과를 증명하기 위해 실제로 실험한 결과 입니다. 그룹의 개수 $g$가 증가할수록 속도는 더 느려지는 것을 볼 수 있습니다.
G3). Network fragmentation reduces degree of parallelism
ResNet 구조나 VGGNet 구조를 생각해보면 단순한 구조가 반복적으로 이루어져있습니다. 반면에 InceptionNet 및 NASNet 기반의 모델들을 보면 복잡한 연산들로 구성되어 있음을 알 수 있습니다. 이와 같이 작은 cell들로 이루어진 복잡한 연산들을 fragmented operator라고 부르기로 합니다. 이러한 연산들은 모델의 정확도에서는 향상을 줄 수 있지만 실질적으로 연산 속도에 악영향을 끼친다고 합니다.


표3에서는 Appendix Figure 1과 같이 다양한 형태의 Fragmented Operation을 정의한 뒤 속도를 비교해봅니다. 결과적으로 1-fragment가 가장 빠른 속도를 가지고 있습니다.
G4). Element-wise Operations are non-negligible
그림2에서 보시는 것처럼 원소별 연산은 생각보다 높은 연산량을 포함하고 있습니다. 특히, GPU에서 큰 것을 볼 수 있습니다.
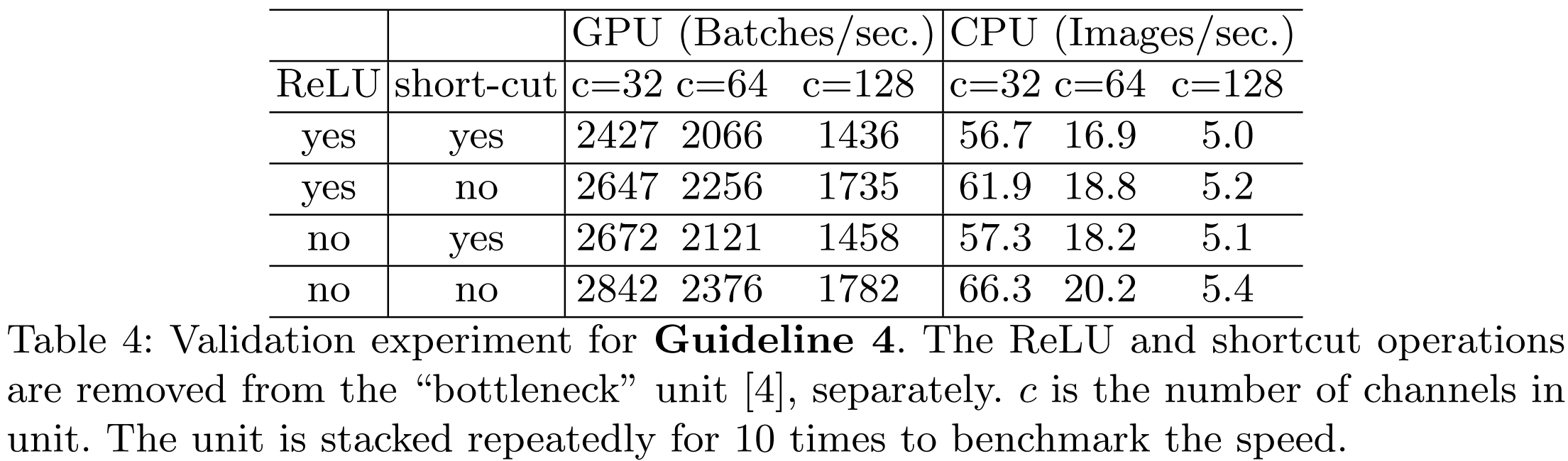
표4는 실제로 ReLU 연산과 shortcut 연산이 없을 때 가장 빠른 것을 볼 수 있습니다.
Conclusion. 결과적으로 모델의 효율을 증가시키기 위해서는 G1) 입력 및 출력 채널의 개수를 동일하게, G2). 그룹의 개수를 신중하게, G3). fragmentation의 최소화, G4). 원소별 연산을 줄이는 것이 중요합니다.
ShuffleNet V2: An Efficient Architecture
1). Review of ShuffleNet V1
ShuffleNet V2를 본격적으로 설명하기에 앞서 ShuffleNet V1에 대한 간략한 설명을 하도록 하겠습니다. 이 모델은 기본적으로 Group Convolution을 수행할 때 여러 개의 블록을 사용하게 됩니다. 따라서, 1개의 그룹이 동일한 그룹에 계속해서 종속되는 문제가 발생할 수 있죠. 이러한 문제를 방지하기 위해 Channel Shuffling 연산을 추가하였습니다. 이를 통해, 모델의 표현력을 증가시키면서 효율성을 크게 증가시켰죠.
2). Channel Split and ShuffleNet V2

ShuffleNet V2는 그림3의 (c)와 같이 기존의 ShuffleNet V1에서 Channel Split이라는 연산도 추가하였습니다. 입력 특징 맵은 처음에 $c - c^{'}$개의 특징 맵과 $c^{'}$개의 특징 맵으로 나뉘어집니다(Channel Split). 이때, G3을 만족시키기 위해 연산을 최소화하여 identity mapping을 수행하는 branch가 적용됩니다. 다른 branch는 입력 채널과 출력 채널의 개수가 동일하게 설정하여 G1을 만족시키죠. 다음으로 그룹 단위에서 $1 \times 1$ 합성곱 연산을 적용하지 않기 때문에 G2도 만족하게 됩니다.

표5는 ShuffleNet V2의 전체 구조를 보여주고 있습니다.
Experiment Results

Implementation Code
import torch
import torch.nn as nn
from layers import BasicConv
class ChannelShuffle(nn.Module):
def __init__(self, groups):
super(ChannelShuffle, self).__init__()
self.groups = groups
def forward(self, x):
batch_size, channels, height, width = x.size()
channels_per_group = channels // self.groups
# Reshape
x = x.view(batch_size, self.groups, channels_per_group, height, width)
# Transpose
x = torch.transpose(x, 1, 2).contiguous()
# Flatten
x = x.view(batch_size, -1, height, width)
return x
class ShuffleBlock(nn.Module):
def __init__(self, in_channels, out_channels, downsample):
super(ShuffleBlock, self).__init__()
self.downsample = downsample
if downsample:
self.branch1 = nn.Sequential(
nn.Conv2d(in_channels, in_channels, kernel_size=3, stride=2, padding=1, groups=in_channels, bias=False),
nn.BatchNorm2d(in_channels),
nn.Conv2d(in_channels, out_channels // 2, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(out_channels // 2), nn.ReLU(inplace=True))
self.branch2 = nn.Sequential(
nn.Conv2d(in_channels, out_channels // 2, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(out_channels // 2), nn.ReLU(inplace=True),
nn.Conv2d(out_channels // 2, out_channels // 2, kernel_size=3, stride=2, padding=1, groups=out_channels // 2, bias=False),
nn.BatchNorm2d(out_channels // 2),
nn.Conv2d(out_channels // 2, out_channels // 2, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(out_channels // 2), nn.ReLU(inplace=True))
else:
assert in_channels == out_channels
self.branch2 = nn.Sequential(
nn.Conv2d(out_channels // 2, out_channels // 2, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(out_channels // 2), nn.ReLU(inplace=True),
nn.Conv2d(out_channels // 2, out_channels // 2, kernel_size=3, stride=1, padding=1, groups=out_channels // 2, bias=False),
nn.BatchNorm2d(out_channels // 2),
nn.Conv2d(out_channels // 2, out_channels // 2, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(out_channels // 2), nn.ReLU(inplace=True))
self.channel_shuffle = ChannelShuffle(groups=2)
def forward(self, x):
if self.downsample:
out = torch.cat([self.branch1(x), self.branch2(x)], dim=1)
else:
channels = x.shape[1]
c = channels // 2
x1 = x[:, :c, :, :]
x2 = x[:, c:, :, :]
out = torch.cat([x1, self.branch2(x2)], dim=1)
return self.channel_shuffle(out )
class ShuffleNetV2(nn.Module):
def __init__(self, input_size, width_multi, num_channels, num_classes):
super(ShuffleNetV2, self).__init__()
assert input_size % 32 == 0
self.stage_repeat = [4, 8, 4]
if width_multi == 0.5: self.stage_out_channels = [-1, 24, 48, 96, 192, 1024]
elif width_multi == 1.0: self.stage_out_channels = [-1, 24, 116, 232, 464, 1024]
elif width_multi == 1.5: self.stage_out_channels = [-1, 24, 176, 352, 704, 1024]
elif width_multi == 2.0: self.stage_out_channels = [-1, 24, 244, 488, 976, 2048]
else: print("the type is error, you should choose 0.5, 1, 1.5 or 2")
# First Convolution Block
self.conv1 = BasicConv(3, self.stage_out_channels[1], kernel_size=3, stride=2, padding=1, bias=False, activation=nn.ReLU(inplace=True), preact=False)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
in_channels = self.stage_out_channels[1]
self.stages = []
for stage_idx in range(len(self.stage_repeat)):
out_channels = self.stage_out_channels[2 + stage_idx]
repeat_num = self.stage_repeat[stage_idx]
for i in range(repeat_num):
if i == 0: self.stages.append(ShuffleBlock(in_channels, out_channels, downsample=True))
else: self.stages.append(ShuffleBlock(in_channels, in_channels, downsample=False))
in_channels = out_channels
self.stages = nn.Sequential(*self.stages)
in_c = self.stage_out_channels[-2]
out_c = self.stage_out_channels[-1]
self.conv5 = BasicConv(in_c, out_c, kernel_size=1, stride=1, padding=0, bias=False, activation=nn.ReLU(inplace=True), preact=False)
self.avg_pool = nn.AvgPool2d(kernel_size=(int)(input_size / 32)) # 如果输入的是224,则此处为7
# fc layer
self.fc = nn.Linear(out_c, num_classes)
def forward(self, x):
x = self.conv1(x)
x = self.maxpool(x)
x = self.stages(x)
x = self.conv5(x)
x = self.avg_pool(x)
x = x.view(-1, self.stage_out_channels[-1])
x = self.fc(x)
return x
if __name__ == '__main__':
model = ShuffleNetV2(input_size=224,
width_multi=1,
num_classes=1000,
num_channels=3)
inp = torch.randn(2, 3, 224, 224)
oup = model(inp)
print(oup.shape)