안녕하세요. 지난 포스팅의 선형대수학 - 고유값과 고유벡터 1에 이어서 설명을 계속해보도록 하겠습니다. 오늘은 주로 고유값 및 고유벡터의 존재성과 성질에 대해서 알아보도록 하죠.
정리1
행렬 $A \in M_{n \times n} (\mathbf{F})$가 주어졌을 때 다음이 성립한다.
(a). 행렬 $A$의 특성방정식의 가장 높은 차수의 계수는 $(-1)^{n}$이다.
(b). 행렬 $A$는 최대 $n$개의 고유값을 가진다.
설명
정리1은 간단하게 생각해보면 당연한 이야기를 하고 있습니다. (a)의 경우에는 저희가 어떤 행렬의 행렬식을 계산할 때 여인수 전개를 적용하기 때문에 얻을 수 있습니다. (b)의 경우에는 일반적으로 $n \times n$ 행렬의 특성방정식은 항상 $n$차 방정식이죠. 하지만, 몇몇 해는 중복해를 가질 수도 있기 때문에 최대 $n$개를 가지게 되는 것 입니다.
정리2
$T$를 벡터공간 $V$ 상에서 선형변환, $\lambda$를 선형변환 $T$의 고유값이라고 하자. 벡터 $v \in V$가 $\lambda에 대응되는 $선형변환 $T$의 고유벡터이기 위해서는 $v \in N(T - \lambda v)$ 이고 $v \neq 0$인 것과 동치이다.
이번에는 고유값과 고유벡터를 이용해서 대각화를 수행하는 방법에 대해서 간단한 예시를 통해 설명해보도록 하겠습니다. 행렬 $A = \begin{pmatrix} 1 & 1 \\ 4 & 1 \end{pmatrix}$이 주어졌다고 했을 때 지난 포스팅의 결과에 의해 저희는 행렬 $A$의 고유값이 $\lambda_{1} = 3$이고 $\lambda_{2} = -1$임을 알았습니다. 다음으로 저희는 각 고유값에 대응되는 고유벡터를 구해야합니다.
1). $\lambda_{1} = 3$이라고 할 때 $\lambda_{1}$에 대응되는 고유벡터를 구하는 방법은 정리2에 의해 $v \in N(A - 3v)$이고 $v \neq 0$인 벡터입니다. 따라서, $v = \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}$라고 할 때 다음과 같이 식을 쓸 수 있습니다.
$$(A - 3I_{2})v = \begin{pmatrix} -2 & 1 \\ 4 & -2 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} = \begin{pmatrix} -2x_{1} + x_{2} \\ 4x_{1} - 2x_{2} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$$
따라서, 이 식을 만족하는 $x_{1}$과 $x_{2}$의 관계식은 $2x_{1} - x_{2} = 0$이므로 이 방정식의 해집합은 다음과 같습니다.
$$\{t \begin{pmatrix} 1 \\ 2 \end{pmatrix} | t \in \mathbb{R}\}$$
즉, $t \in \mathbb{R}$에 대해서 모든 $t \begin{pmatrix} 1 \\ 2 \end{pmatrix}$는 $\lambda_{1} = 3$에 대응되는 고유벡터이므로 가장 간단하게 하기 위해 $t = 1$로 고정하고 $v_{1} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}$를 $\lambda_{1} = 3$에 대응되는 고유벡터라고 하겠습니다.
2). $\lambda_{2} = -1$이라고 할 때 $\lambda_{2}$에 대응되는 고유벡터를 구하는 방법은 정리2에 의해 $v \in N(A + v)$이고 $v \neq 0$인 벡터입니다. 따라서, $v = \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}$라고 할 때 다음과 같이 식을 쓸 수 있습니다.
$$(A - 3I_{2})v = \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} = \begin{pmatrix} 2x_{1} + x_{2} \\ 4x_{1} + 2x_{2} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$$
따라서, 이 식을 만족하는 $x_{1}$과 $x_{2}$의 관계식은 $2x_{1} + x_{2} = 0$이므로 이 방정식의 해집합은 다음과 같습니다.
$$\{t \begin{pmatrix} 1 \\ -2 \end{pmatrix} | t \in \mathbb{R}\}$$
즉, $t \in \mathbb{R}$에 대해서 모든 $t \begin{pmatrix} 1 \\ -2 \end{pmatrix}$는 $\lambda_{2} = -1$에 대응되는 고유벡터이므로 가장 간단하게 하기 위해 $t = 1$로 고정하고 $v_{2} = \begin{pmatrix} 1 \\ -2 \end{pmatrix}$를 $\lambda_{2} = -1$에 대응되는 고유벡터라고 하겠습니다.
그러므로 $\beta = \{\begin{pmatrix} 1 \\ 2 \end{pmatrix}, \begin{pmatrix} 1 \\ -2 \end{pmatrix}\}$는 행렬 $A$의 고유벡터의 집합이 됩니다. 이제 저희는 $Av = \lambda v$라는 식을 이용해서 대각화를 수행할 수 있습니다. 선형대수학 - 좌표변환 행렬의 정리2에 의해 $Q^{-1}AQ = D$라고 쓸 수 있습니다. 여기서 저희는 새로운 좌표계를 $\beta$로 설정한 뒤 좌표를 변환한 결과가 각 고유벡터에 대한 고유값이되므로 다음과 같이 쓸 수 있습니다.
$$\begin{pmatrix} 1 & 1 \\ 2 & -2 \end{pmatrix}^{-1} \begin{pmatrix} 1 & 1 \\ 4 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 \\ 2 & -2 \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & -1 \end{pmatrix}$$
즉, 저희는 행렬 $A$를 고유벡터로 구성된 행렬 $Q$를 이용해서 대각행렬로 바꾸는 과정인 대각화에 성공하였습니다. 그렇다면 선형변환 $T$의 고유벡터는 어떻게 구할까요? 고유값까지는 $T$에 대응되는 행렬로 변환함으로써 쉽게 구할 수 있었습니다. 하지만, 고유벡터부터는 살짝 이야기가 달라집니다. 아래의 그림을 참고해주세요.
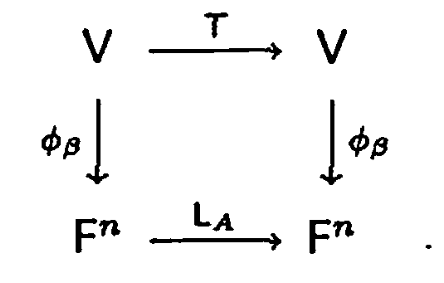
위 그림에서 저희가 원하는 것을 알려주고 있습니다. 저희는 $V$에 속하는 $T$의 고유벡터를 구하고 싶습니다. 하지만 저희는 $A$의 고유값을 구했기 때문에 $L_{A}$의 고유값에 대응되는 고유벡터는 구할 수 있죠. 이때, 선형대수학 - 역변환과 동형사상의 정리5에 의해 $V$와 $\mathbf{F}^{n}$ 사이에는 동형사상 $\phi_{\beta}$가 존재합니다. 따라서, 저희는 $L_{A}$의 고유벡터를 얻은 뒤 $\phi_{\beta}$의 역변환인 $\phi_{\beta}^{-1}$을 적용하면 선형변환 $T$의 고유벡터를 얻을 수 있습니다. 이 과정을 수식으로 정리하면 $T(v) = \lambda v$에 대해서 다음과 같이 쓸 수 있습니다.
$$A \phi_{\beta} (v) = L_{A} \phi_{\beta} (v) = \phi_{\beta} T(v) = \phi_{\beta} (\lambda v) = \lambda \phi_{\beta} (v)$$
이제 간단한 예시를 통해 선형변환 $T$의 고유벡터를 구해보도록 하겠습니다. 선형변환 $T : P_{2}(\mathbb{R}) \rightarrow P_{2} (\mathbb{R})$을 $T(f(x)) = f(x) + (x + 1) f^{'}(x)$로 정의하도록 하겠습니다. $\beta$를 $P_{2}(\mathbb{R})$의 표준순서기저라고 두면 $A = [T]_{\beta} = \begin{pmatrix} 1 & 1 & 0 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{pmatrix}$으로 쓸 수 있습니다. 이제 행렬 $A$의 고유값을 구해볼 수 있겠네요.
$$\text{det} (A - \lambda I_{3}) = \text{det} \begin{pmatrix} 1 - \lambda & 1 & 0 \\ 0 & 2 - \lambda & 2 \\ 0 & 0 & 3 - \lambda \end{pmatrix} = -(\lambda - 1)(\lambda - 2)(\lambda - 3) = 0$$
따라서, 선형변환 $T$의 고유값은 $\lambda_{1} = 1, \lambda_{2} = 2, \lambda_{3} = 3$입니다. 이제 행렬 $A$의 각 고유값에 대응되는 고유벡터를 먼저 구해보도록 하겠습니다.
1). $\lambda_{1} = 1$ 그리고 $v = \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix}$라고 할 때 다음과 같이 식을 쓸 수 있습니다.
$$(A - I_{3})v = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 1 & 2 \\ 0 & 0 & 3 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix} = \begin{pmatrix} x_{2} \\ x_{2} + 2x_{3} \\ 3x_{3} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0\end{pmatrix}$$
따라서, 이 식을 만족하는 $x_{1}, x_{2}, x_{3}$의 관계식은 $x_{2} = x_{3} = 0$이므로 이 방정식의 해집합은 다음과 같습니다.
$$\{t \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} | t \in \mathbb{R}\}$$
2). $\lambda_{2} = 2$ 그리고 $v = \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix}$라고 할 때 다음과 같이 식을 쓸 수 있습니다.
$$(A - 2I_{3})v = \begin{pmatrix} -1 & 1 & 0 \\ 0 & 0 & 2 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix} = \begin{pmatrix} -x_{1} + x_{2} \\ 2x_{3} \\ x_{3} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0\end{pmatrix}$$
따라서, 이 식을 만족하는 $x_{1}, x_{2}, x_{3}$의 관계식은 $-x_{1} + x_{2} = 0, x_{3} = 0$이므로 이 방정식의 해집합은 다음과 같습니다.
$$\{t \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} | t \in \mathbb{R}\}$$
3). $\lambda_{3} = 3$ 그리고 $v = \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix}$라고 할 때 다음과 같이 식을 쓸 수 있습니다.
$$(A - 3I_{3})v = \begin{pmatrix} -2 & 1 & 0 \\ 0 & -1 & 2 \\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix} = \begin{pmatrix} -2x_{1} + x_{2} \\ -x_{2} + 2x_{3} \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0\end{pmatrix}$$
따라서, 이 식을 만족하는 $x_{1}, x_{2}, x_{3}$의 관계식은 $-2x_{1} + x_{2} = 0, -x_{2} + 2x_{3} = 0$이므로 이 방정식의 해집합은 다음과 같습니다.
$$\{t \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} | t \in \mathbb{R}\}$$
가장 간단하게 각 고유값에 대응되는 행렬 $A$의 고유벡터는 $\{\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}, \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}\}$가 됩니다. 이제 마지막으로 저희가 해줄 것은 각 고유벡터에 $\phi_{\beta}^{-1}$을 적용하는 것이죠.
$$\phi_{\beta}^{-1} \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = 1$$
$$\phi_{\beta}^{-1} \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} = 1 + x$$
$$\phi_{\beta}^{-1} \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} = 1 + 2x + x^{2}$$
따라서, 선형변환 $T$의 고유값 $\lambda_{1} = 1, \lambda_{2} = 2, \lambda_{3} = 3$에 대응되는 각 고유벡터는 $v_{1} = 1, v_{2} = 1 + x, v_{3} = 1 + 2x + x^{2}$입니다.
참고문헌
Linear Algebra (Stephan. H)
'수학 > 선형대수학' 카테고리의 다른 글
| 선형대수학 - 대각화 2 (0) | 2023.03.05 |
|---|---|
| 선형대수학 - 대각화 1 (0) | 2023.03.05 |
| 선형대수학 - 행렬식의 새로운 관점 (0) | 2023.02.06 |
| 선형대수학 - 행렬식의 성질 (0) | 2023.01.22 |
| 선형대수학 - 행렬식과 기본행렬연산 (0) | 2023.01.19 |
