안녕하세요. 지난 포스티의 미적분학 - 유향곡면에서는 곡면에서의 면적분을 설명한 뒤 이를 벡터장으로 확장해보았습니다. 이 과정에서 필수적으로 곡면의 방향성이 존재해야하며 주어진 곡면을 통과하는 벡터장의 유량 (flux)를 계산할 수 있었습니다. 오늘은 그린 정리 (Green's Theorem)의 일반화된 버전인 스토크스의 정리 (Stokes' Theorem)에 대해서 알아보겠습니다.
정리1. 스토크스의 정리(Stokes' Theorem)
곡면 $S$를 조각끼리 부드럽고 양의 방향성이 존재하는 유계 단순연결곡선 $C$에 의해 제한이 생기는 조각끼리 부드러운 유향곡면이라고 하자. 벡터함수 $\mathbf{F}$를 각 성분함수가 3차원 실수공간 $\mathbf{R}^{3}$에서 유향곡면 $S$를 포함하는 영역에서 연속 편도함수는 벡터장이라고 할 때, 아래의 식이 성립한다.
$$\int_{C} \mathbf{F} \cdot d\mathbf{r} = \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S} \tag{1}$$
설명
흔히들 스토크스의 정리를 그린 정리의 확장판이라고 많이 설명합니다. 차이점을 분석해보도록 하죠. 벡터함수 $\mathbf{F} = P \mathbf{i} + Q \mathbf{j}$라고 할 때 그린 정리를 아래와 같이 쓸 수 있습니다.
$$\int_{C} \mathbf{F} \cdot d\mathbf{r} = \iint_{D} \left( \text{curl } \mathbf{F} \right) \mathbf{k} \; dA$$
잘 보시면 그린 정리와 스토크스 정리 모두 좌항은 동일합니다. 하지만, 달라지는 것은 우항이죠. 그린 정리는 정의역인 평면 $D$에서 해당 정의역을 둘러쌓은 곡선 $C$와 관련된 정리이지만 스토크스 정리는 유향곡면 $S$에서 해당 곡면을 둘러쌓은 곡선 $C$와 관련된 정리입니다. 즉, 스토크스 정리는 선적분을 면적분으로 벡터장의 회전에 대한 유향곡면 $S$에서의 면적분으로 바꾸어서 계산할 수 있다는 것 입니다. 가끔 곡면 $S$의 경계선을 $\partial$을 이용해서 $C = \partial S$와 같이 쓸 수 있습니다.
$$\int_{\partial S} \mathbf{F} \cdot d\mathbf{r} = \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S}$$
그렇다면 왜 스토크스의 정리가 그린 정리의 확장판이라고 부를까요? 그 이유는 우항인 면적분에 있습니다. 만약, 곡면 $S$가 평평한 단순 평면이라고 하면 이는 기존에 그린 정리의 조건과 동일한 것을 볼 수 있습니다. 따라서, 스토스크의 정리를 아래와 같이 쓸 수 있죠.
$$\int_{C} \mathbf{F} \cdot d\mathbf{r} = \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S} = \iint_{S} \left( \text{curl } \mathbf{F} \right) \cdot \mathbf{k} \; dA$$
왜냐하면 $\mathbf{n}$을 유향곡면 $S$의 법선벡터라고 할 때 $d\mathbf{S} = \mathbf{n} \; dS$인데, 단순 평면에서는 $\mathbf{n} = \mathbf{k}$이기 때문이죠.
이제는 스토크스의 정리를 증명해보도록 하겠습니다. 그린 정리와 마찬가지로 일반화된 증명은 많이 어렵기 때문에 특별한 케이스에 대한 스토크스의 정리를 증명해보도록 하죠.
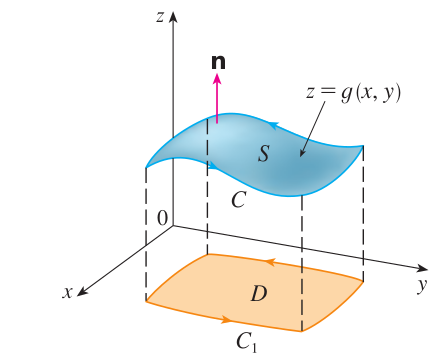
위 그림과 함께 보시면 이해가 훨씬 빠를 수 있습니다. 곡면 $S$가 특별히 정의역 $(x, y) \in D$에 대해서 $z = g(x, y)$로 표현될 수 있다고 가정하겠습니다. 이때, 함수 $g$는 연속인 2계 편도함수를 가지고 $D$가 곡선 $C_{1}$에 둘러쌓인 단순 연결 영역 공간이라고 가정하겠습니다. 여기서 곡선 $C_{1}$은 곡면 $S$를 둘러쌓은 곡선 $C$에 대응되는 곡선입니다. 그리고 유향곡면 $S$의 방향이 위로 향하면 곡선 $C$는 양의 방향을 가지게 되고 이러한 곡선 $C$의 방향성은 곡선 $C_{1}$에도 보존됩니다. 또한 벡터장 $\mathbf{F} = P \mathbf{i} + Q \mathbf{j} + R \mathbf{k}$이 주어졌을 때 각 성분함수 $P, Q$ 그리고 $R$이 모두 연속인 편도함수를 가진다고 가정하겠습니다.
여기서 저희는 곡면 $S$가 함수의 그래프로 표현되기 때문에 미적분학 - 유향곡면에서 수식 (6)을 적용할 수 있습니다. 또한 미적분학 - 회전과 발산에서 보았던 회전 $\text{curl}$의 정의를 이용할 수 있죠.
$$\text{curl } \mathbf{F} = \left(\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}\right) \mathbf{i} + \left(\frac{\partial P} {\partial z} - \frac{\partial R}{\partial x}\right) \mathbf{j} + \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \mathbf{k} \tag{2}$$
이 식을 수식 (1)의 우항에 대입해보도록 하겠습니다.
$$\begin{align*} \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S} \\ &= \iint_{D} \left[ -\left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) \frac{\partial z}{\partial x} - \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) \frac{\partial z}{\partial y} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \right] \; dA \end{align*}$$
다음으로 할 일은 수식 (1)의 좌항을 손봐야합니다. 이때, 벡터장 $\mathbf{F}$가 그래프로 표현되기 때문에 $a \le t \le b$에 대해서 $x = x(t), y = y(t)$이 곡선 $C_{1}$의 매개변수 표현이 됩니다. 그러면 곡선 $C$의 매개변수 표현은 무엇일까요? 아주 단순하게 $z = g(x(t), y(t))$를 추가해주면 됩니다. 이제 선적분을 계산해보도록 하죠. 여기서는 주로 연쇄법칙을 활용하여 식을 풀어줍니다.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \int_{a}^{b} \left( P \frac{dx}{dt} + Q \frac{dy}{dt} + R \frac{dz}{dt} \right) \; dt \\ &= \int_{a}^{b} \left[ P \frac{dx}{dt} + Q \frac{dy}{dt} + R \left( \frac{\partial z}{\partial x} \frac{dx}{dt} + \frac{\partial z}{\partial y} \frac{dy}{dt} \right) \right] \; dt \\ &= \int_{a}^{b} \left[ \left( P + R \frac{\partial z}{\partial x} \right) \frac{dx}{dt} + \left( Q + R \frac{\partial z}{\partial y} \right) \frac{dy}{dt} \right] \; dt \\ &= \int_{C_{1}} \left( P + R \frac{\partial z}{\partial x}\right) \; dx + \left( Q + R \frac{\partial z}{\partial y} \right) \; dy \\ &= \iint_{D} \left[ \frac{\partial}{\partial x} \left( Q + R \frac{dz}{dy} \right) - \frac{\partial}{\partial y} \left( P + R \frac{dz}{dx} \right) \right] \; dA \end{align*} \tag{3}$$
마지막 식 변환은 그린 정리를 적용하였습니다. 마지막으로 저희는 수식 (3)에서 연쇄법칙을 적용해야합니다. 여기서 기억해야할 점은 성분함수 $P, Q, R$은 모두 $x, y, z$에 대한 함수이며 $z$는 $x, y$에 대한 함수라는 점 입니다.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \iint_{D} \left[ \frac{\partial}{\partial x} \left( Q + R \frac{dz}{dy} \right) - \frac{\partial}{\partial y} \left( P + R \frac{dz}{dx} \right) \right] \; dA \\ &= \iint_{D} \left[ \left(\frac{\partial Q}{\partial x} + \frac{\partial}{\partial y} \left( R\frac{\partial z}{\partial y} \right)\right) - \left( \frac{\partial P}{\partial y} + \frac{\partial}{\partial y} \left(R\frac{\partial z}{\partial x}\right) \right)\right] \; dA \\ &= \iint_{D} \left( \frac{\partial Q}{\partial x} + \frac{\partial Q}{\partial z} \frac{\partial Q}{\partial z} \frac{\partial z}{\partial x} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial x} \frac{\partial z}{\partial y} + R \frac{\partial^{2} z}{\partial x \partial y} \right) \\ & - \left( \frac{\partial P}{\partial y} + \frac{\partial P}{\partial z} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial y} \frac{\partial y}{\partial z} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial y} \frac{\partial z}{\partial x} + R \frac{\partial^{2} z}{\partial y \partial x} \right)\end{align*} \; dA \tag{4}$$
수식 (4)에서 성분함수들은 연속인 편도함수가 존재하기 때문에 클레로의 정리를 적용할 수 있습니다. 따라서, 위 식을 정리하면 아래와 같죠.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \iint_{D} \left( \frac{\partial Q}{\partial x} + \frac{\partial Q}{\partial z} \frac{\partial Q}{\partial z} \frac{\partial z}{\partial x} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial x} \frac{\partial z}{\partial y} + R \frac{\partial^{2} z}{\partial x \partial y} \right) \\ & - \left( \frac{\partial P}{\partial y} + \frac{\partial P}{\partial z} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial y} \frac{\partial y}{\partial z} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial y} \frac{\partial z}{\partial x} + R \frac{\partial^{2} z}{\partial y \partial x} \right) \\ &= \iint_{D} \left[ \left( \frac{\partial Q}{\partial x} + \frac{\partial Q}{\partial x} \frac{\partial z}{\partial x} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial y} \right) - \left( \frac{\partial P}{\partial y} + \frac{\partial P}{\partial z} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial x}\right) \right] \\ &= \iint_{D} \left[ -\left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) \frac{\partial z}{\partial x} - \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) \frac{\partial z}{\partial y} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \right] \; dA \\ &= \iint_{S} \text{curl } \mathbf{F} \; d\mathbf{S} \end{align*} \tag{5}$$
이로써 특별한 케이스에 대한 스토크스의 정리는 증명됩니다.
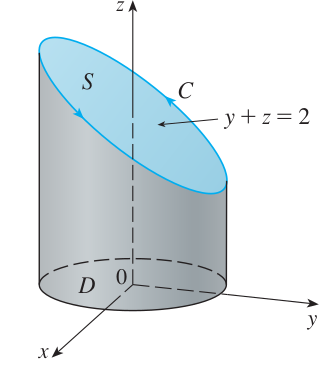
예제1. 벡터장 $\mathbf{F} = -y^{2} \mathbf{i} + x \mathbf{j} + z^{2} \mathbf{k}$와 곡선 $C$가 평면 $y + z = 2$와 원기둥 $x^{2} + y^{2} = 1$의 교집합으로 이루어졌다고 할 때 선적분 $\int_{C} \mathbf{F} \cdot d\mathbf{r}$을 계산하라.
STEP1. 곡선 $C$를 3차원으로 그리기
STEP2. 스토크스의 정리 적용하기
먼저, 벡터장 $\mathbf{F}$의 회전을 계산한다.
$$\begin{align*} \text{curl } \mathbf{F} &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ -y^{2} & x & z^{2} \end{vmatrix} \\ &= (1 + 2y) \mathbf{k} \end{align*}$$
곡선 $C$에 의해 만들어지는 곡면 $S$는 원기둥의 단면인 $y + z = 2$이다. 또한 곡면 $S$를 $xy$ 평면으로 사영시켰을 때 영역 $D = \{(x, y) | x^{2} + y^{2} \le 1\}$이다.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S} \\ &= \iint_{D} (1 + 2y) \; dA \\ &= \int_{0}^{2\pi} \int_{0}^{1} (1 + 2r\sin(\theta)) r \; drd\theta \\ &= \int_{0}^{2\pi} \left[ \frac{r^{2}}{2} + 2\frac{r^{3}}{3}\sin(\theta) \right]_{0}^{1} \; d\theta \\ &= \int_{0}^{2\pi} \left( \frac{1}{2} + \frac{2}{3}\sin(\theta) \right) \; d\theta \\ &= \frac{1}{2} \left( 2\pi \right) + 0 = \pi \end{align*}$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 목차 (0) | 2022.08.03 |
|---|---|
| 미적분학 - 발산 정리 (0) | 2022.08.02 |
| 미적분학 - 유향곡면 (0) | 2022.07.29 |
| 미적분학 - 면적분 (0) | 2022.07.28 |
| 미적분학 - 매개변수 곡면 (0) | 2022.07.27 |
안녕하세요. 지난 포스티의 미적분학 - 유향곡면에서는 곡면에서의 면적분을 설명한 뒤 이를 벡터장으로 확장해보았습니다. 이 과정에서 필수적으로 곡면의 방향성이 존재해야하며 주어진 곡면을 통과하는 벡터장의 유량 (flux)를 계산할 수 있었습니다. 오늘은 그린 정리 (Green's Theorem)의 일반화된 버전인 스토크스의 정리 (Stokes' Theorem)에 대해서 알아보겠습니다.
정리1. 스토크스의 정리(Stokes' Theorem)
곡면 $S$를 조각끼리 부드럽고 양의 방향성이 존재하는 유계 단순연결곡선 $C$에 의해 제한이 생기는 조각끼리 부드러운 유향곡면이라고 하자. 벡터함수 $\mathbf{F}$를 각 성분함수가 3차원 실수공간 $\mathbf{R}^{3}$에서 유향곡면 $S$를 포함하는 영역에서 연속 편도함수는 벡터장이라고 할 때, 아래의 식이 성립한다.
$$\int_{C} \mathbf{F} \cdot d\mathbf{r} = \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S} \tag{1}$$
설명
흔히들 스토크스의 정리를 그린 정리의 확장판이라고 많이 설명합니다. 차이점을 분석해보도록 하죠. 벡터함수 $\mathbf{F} = P \mathbf{i} + Q \mathbf{j}$라고 할 때 그린 정리를 아래와 같이 쓸 수 있습니다.
$$\int_{C} \mathbf{F} \cdot d\mathbf{r} = \iint_{D} \left( \text{curl } \mathbf{F} \right) \mathbf{k} \; dA$$
잘 보시면 그린 정리와 스토크스 정리 모두 좌항은 동일합니다. 하지만, 달라지는 것은 우항이죠. 그린 정리는 정의역인 평면 $D$에서 해당 정의역을 둘러쌓은 곡선 $C$와 관련된 정리이지만 스토크스 정리는 유향곡면 $S$에서 해당 곡면을 둘러쌓은 곡선 $C$와 관련된 정리입니다. 즉, 스토크스 정리는 선적분을 면적분으로 벡터장의 회전에 대한 유향곡면 $S$에서의 면적분으로 바꾸어서 계산할 수 있다는 것 입니다. 가끔 곡면 $S$의 경계선을 $\partial$을 이용해서 $C = \partial S$와 같이 쓸 수 있습니다.
$$\int_{\partial S} \mathbf{F} \cdot d\mathbf{r} = \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S}$$
그렇다면 왜 스토크스의 정리가 그린 정리의 확장판이라고 부를까요? 그 이유는 우항인 면적분에 있습니다. 만약, 곡면 $S$가 평평한 단순 평면이라고 하면 이는 기존에 그린 정리의 조건과 동일한 것을 볼 수 있습니다. 따라서, 스토스크의 정리를 아래와 같이 쓸 수 있죠.
$$\int_{C} \mathbf{F} \cdot d\mathbf{r} = \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S} = \iint_{S} \left( \text{curl } \mathbf{F} \right) \cdot \mathbf{k} \; dA$$
왜냐하면 $\mathbf{n}$을 유향곡면 $S$의 법선벡터라고 할 때 $d\mathbf{S} = \mathbf{n} \; dS$인데, 단순 평면에서는 $\mathbf{n} = \mathbf{k}$이기 때문이죠.
이제는 스토크스의 정리를 증명해보도록 하겠습니다. 그린 정리와 마찬가지로 일반화된 증명은 많이 어렵기 때문에 특별한 케이스에 대한 스토크스의 정리를 증명해보도록 하죠.

위 그림과 함께 보시면 이해가 훨씬 빠를 수 있습니다. 곡면 $S$가 특별히 정의역 $(x, y) \in D$에 대해서 $z = g(x, y)$로 표현될 수 있다고 가정하겠습니다. 이때, 함수 $g$는 연속인 2계 편도함수를 가지고 $D$가 곡선 $C_{1}$에 둘러쌓인 단순 연결 영역 공간이라고 가정하겠습니다. 여기서 곡선 $C_{1}$은 곡면 $S$를 둘러쌓은 곡선 $C$에 대응되는 곡선입니다. 그리고 유향곡면 $S$의 방향이 위로 향하면 곡선 $C$는 양의 방향을 가지게 되고 이러한 곡선 $C$의 방향성은 곡선 $C_{1}$에도 보존됩니다. 또한 벡터장 $\mathbf{F} = P \mathbf{i} + Q \mathbf{j} + R \mathbf{k}$이 주어졌을 때 각 성분함수 $P, Q$ 그리고 $R$이 모두 연속인 편도함수를 가진다고 가정하겠습니다.
여기서 저희는 곡면 $S$가 함수의 그래프로 표현되기 때문에 미적분학 - 유향곡면에서 수식 (6)을 적용할 수 있습니다. 또한 미적분학 - 회전과 발산에서 보았던 회전 $\text{curl}$의 정의를 이용할 수 있죠.
$$\text{curl } \mathbf{F} = \left(\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}\right) \mathbf{i} + \left(\frac{\partial P} {\partial z} - \frac{\partial R}{\partial x}\right) \mathbf{j} + \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \mathbf{k} \tag{2}$$
이 식을 수식 (1)의 우항에 대입해보도록 하겠습니다.
$$\begin{align*} \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S} \\ &= \iint_{D} \left[ -\left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) \frac{\partial z}{\partial x} - \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) \frac{\partial z}{\partial y} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \right] \; dA \end{align*}$$
다음으로 할 일은 수식 (1)의 좌항을 손봐야합니다. 이때, 벡터장 $\mathbf{F}$가 그래프로 표현되기 때문에 $a \le t \le b$에 대해서 $x = x(t), y = y(t)$이 곡선 $C_{1}$의 매개변수 표현이 됩니다. 그러면 곡선 $C$의 매개변수 표현은 무엇일까요? 아주 단순하게 $z = g(x(t), y(t))$를 추가해주면 됩니다. 이제 선적분을 계산해보도록 하죠. 여기서는 주로 연쇄법칙을 활용하여 식을 풀어줍니다.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \int_{a}^{b} \left( P \frac{dx}{dt} + Q \frac{dy}{dt} + R \frac{dz}{dt} \right) \; dt \\ &= \int_{a}^{b} \left[ P \frac{dx}{dt} + Q \frac{dy}{dt} + R \left( \frac{\partial z}{\partial x} \frac{dx}{dt} + \frac{\partial z}{\partial y} \frac{dy}{dt} \right) \right] \; dt \\ &= \int_{a}^{b} \left[ \left( P + R \frac{\partial z}{\partial x} \right) \frac{dx}{dt} + \left( Q + R \frac{\partial z}{\partial y} \right) \frac{dy}{dt} \right] \; dt \\ &= \int_{C_{1}} \left( P + R \frac{\partial z}{\partial x}\right) \; dx + \left( Q + R \frac{\partial z}{\partial y} \right) \; dy \\ &= \iint_{D} \left[ \frac{\partial}{\partial x} \left( Q + R \frac{dz}{dy} \right) - \frac{\partial}{\partial y} \left( P + R \frac{dz}{dx} \right) \right] \; dA \end{align*} \tag{3}$$
마지막 식 변환은 그린 정리를 적용하였습니다. 마지막으로 저희는 수식 (3)에서 연쇄법칙을 적용해야합니다. 여기서 기억해야할 점은 성분함수 $P, Q, R$은 모두 $x, y, z$에 대한 함수이며 $z$는 $x, y$에 대한 함수라는 점 입니다.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \iint_{D} \left[ \frac{\partial}{\partial x} \left( Q + R \frac{dz}{dy} \right) - \frac{\partial}{\partial y} \left( P + R \frac{dz}{dx} \right) \right] \; dA \\ &= \iint_{D} \left[ \left(\frac{\partial Q}{\partial x} + \frac{\partial}{\partial y} \left( R\frac{\partial z}{\partial y} \right)\right) - \left( \frac{\partial P}{\partial y} + \frac{\partial}{\partial y} \left(R\frac{\partial z}{\partial x}\right) \right)\right] \; dA \\ &= \iint_{D} \left( \frac{\partial Q}{\partial x} + \frac{\partial Q}{\partial z} \frac{\partial Q}{\partial z} \frac{\partial z}{\partial x} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial x} \frac{\partial z}{\partial y} + R \frac{\partial^{2} z}{\partial x \partial y} \right) \\ & - \left( \frac{\partial P}{\partial y} + \frac{\partial P}{\partial z} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial y} \frac{\partial y}{\partial z} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial y} \frac{\partial z}{\partial x} + R \frac{\partial^{2} z}{\partial y \partial x} \right)\end{align*} \; dA \tag{4}$$
수식 (4)에서 성분함수들은 연속인 편도함수가 존재하기 때문에 클레로의 정리를 적용할 수 있습니다. 따라서, 위 식을 정리하면 아래와 같죠.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \iint_{D} \left( \frac{\partial Q}{\partial x} + \frac{\partial Q}{\partial z} \frac{\partial Q}{\partial z} \frac{\partial z}{\partial x} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial x} \frac{\partial z}{\partial y} + R \frac{\partial^{2} z}{\partial x \partial y} \right) \\ & - \left( \frac{\partial P}{\partial y} + \frac{\partial P}{\partial z} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial y} \frac{\partial y}{\partial z} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial y} \frac{\partial z}{\partial x} + R \frac{\partial^{2} z}{\partial y \partial x} \right) \\ &= \iint_{D} \left[ \left( \frac{\partial Q}{\partial x} + \frac{\partial Q}{\partial x} \frac{\partial z}{\partial x} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial y} \right) - \left( \frac{\partial P}{\partial y} + \frac{\partial P}{\partial z} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial x}\right) \right] \\ &= \iint_{D} \left[ -\left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) \frac{\partial z}{\partial x} - \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) \frac{\partial z}{\partial y} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \right] \; dA \\ &= \iint_{S} \text{curl } \mathbf{F} \; d\mathbf{S} \end{align*} \tag{5}$$
이로써 특별한 케이스에 대한 스토크스의 정리는 증명됩니다.
예제1. 벡터장 $\mathbf{F} = -y^{2} \mathbf{i} + x \mathbf{j} + z^{2} \mathbf{k}$와 곡선 $C$가 평면 $y + z = 2$와 원기둥 $x^{2} + y^{2} = 1$의 교집합으로 이루어졌다고 할 때 선적분 $\int_{C} \mathbf{F} \cdot d\mathbf{r}$을 계산하라.
STEP1. 곡선 $C$를 3차원으로 그리기

STEP2. 스토크스의 정리 적용하기
먼저, 벡터장 $\mathbf{F}$의 회전을 계산한다.
$$\begin{align*} \text{curl } \mathbf{F} &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ -y^{2} & x & z^{2} \end{vmatrix} \\ &= (1 + 2y) \mathbf{k} \end{align*}$$
곡선 $C$에 의해 만들어지는 곡면 $S$는 원기둥의 단면인 $y + z = 2$이다. 또한 곡면 $S$를 $xy$ 평면으로 사영시켰을 때 영역 $D = \{(x, y) | x^{2} + y^{2} \le 1\}$이다.
$$\begin{align*} \int_{C} \mathbf{F} \cdot d\mathbf{r} &= \iint_{S} \text{curl } \mathbf{F} \cdot d\mathbf{S} \\ &= \iint_{D} (1 + 2y) \; dA \\ &= \int_{0}^{2\pi} \int_{0}^{1} (1 + 2r\sin(\theta)) r \; drd\theta \\ &= \int_{0}^{2\pi} \left[ \frac{r^{2}}{2} + 2\frac{r^{3}}{3}\sin(\theta) \right]_{0}^{1} \; d\theta \\ &= \int_{0}^{2\pi} \left( \frac{1}{2} + \frac{2}{3}\sin(\theta) \right) \; d\theta \\ &= \frac{1}{2} \left( 2\pi \right) + 0 = \pi \end{align*}$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 목차 (0) | 2022.08.03 |
|---|---|
| 미적분학 - 발산 정리 (0) | 2022.08.02 |
| 미적분학 - 유향곡면 (0) | 2022.07.29 |
| 미적분학 - 면적분 (0) | 2022.07.28 |
| 미적분학 - 매개변수 곡면 (0) | 2022.07.27 |
