안녕하세요. 지난 포스팅의 미적분학 - 삼중적분에서는 3개의 변수 $(x, y, z)$를 가지는 함수 $w = f(x, y, z)$에 대한 삼중적분을 해보았습니다. 오늘은 이중적분을 극좌표계에서 했듯이 삼중적분을 다른 좌표계에서 해보도록 하겠습니다. 삼중적분에서 자주 사용되는 좌표계는 원기둥좌표계입니다. 오늘은 이것에 대해서 알아보도록 하죠.

일단 원기둥좌표계(Cylinder Coordinate)부터 알아보아야할 거 같습니다. 기본적인 구조는 극좌표계(Polar Coordinate)와 동일합니다. 미적분학 - 극좌표계에서 보았듯이 좌표계 변환을 다시 보도록 하겠습니다.
$$x = r\cos(\theta), y = r\sin(\theta)$$
여기서 원기등좌표계는 추가적으로 $z$축을 추가하여 $(r, \theta, z)$를 기반으로한 좌표계를 구성하게 됩니다. 이를 전체적으로 정리하면 아래와 같습니다.
$$x = r\cos(\theta), y = r\sin(\theta), z = z$$
그리고 원기둥좌표계에서 다시 직교좌표계로 돌리는 방법도 생각해봐야겠죠.
$$r = \sqrt{x^{2} + y^{2}}, \theta = \arctan \left(\frac{y}{x}\right), z = z$$
결과를 보시면 단순히 원기둥좌표계는 $xy$평면만 극좌표로 변환하고 나머지 하나인 $z$축은 변화시키지 않은 것입니다.
예제1. 원기둥좌표계 $(2, \frac{2\pi}{3}, 1)$이 주어졌을 때, 직교좌표계로 변환하시오.
1). $x = r\cos(\theta) = 2\cos\left(\frac{2\pi}{3}\right) = 2 \cdot \left(-\frac{1}{2}\right) = -1$
2). $y = r\sin(\theta) = 2\sin\left(\frac{2\pi}{3}\right) = 2 \cdot \frac{\sqrt{3}}{2} = \sqrt{3}$
3). $z = 1$
따라서, 직교좌표계에서의 좌표는 $(-1, \sqrt{3}, 1)$이다.
예제2. 직교표계 $(3, -3, 7)$이 주어졌을 때, 원기둥좌표계로 변환하시오.
1). $r = \sqrt{x^{2} + y^{2}} = \sqrt{3^{2} + (-3)^{2}} = 3\sqrt{2}$
2). $\theta = \arctan \left(\frac{y}{x} \right) = \arctan \left(-1\right) = \frac{7\pi}{4} + 2n\pi$
3). $z = 7$
따라서, 임의의 정수 $n$에 대해서 원기둥좌표계에서의 좌표는 $(3\sqrt{2}, \frac{7\pi}{4} + 2n\pi, 7)$이다.
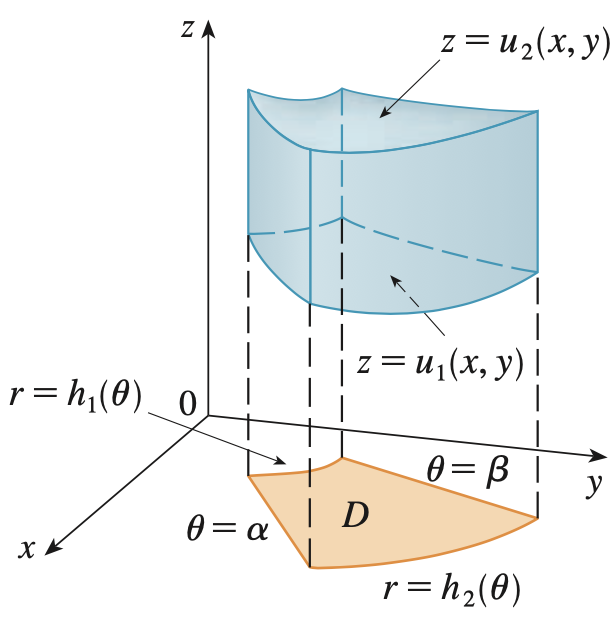
이번에는 원기둥좌표계에서의 삼중적분을 수행하는 방법에 대해서 알아보도록 하겠습니다. 일단, 영역 $D$를 극좌표로 표기된 영역이라고 하겠습니다. 그리고 $z$의 범위가 두 함수 $u_{1}$과 $u_{2}$에 의해 발생한다고 생각하겠습니다. 그러면 저희는 적분해야하는 영역 $E$를 정의할 수 있죠.
$$E = \{(x, y) | (x, y) \in D, u_{1}(x, y) \le z \le u_{2}(x, y)\}$$
여기서 영역 $D = \{(r, \theta) | \alpha \le \theta \le \beta, h_{1}(\theta) \le r \le h_{2}(\theta)\}$입니다.따라서 이 영역에 대한 삼중적분은 아래와 같이 정의됩니다.
$$\int\int\int_{E} f(x, y, z) \; dV = \int_{\alpha}^{\beta} \int_{h_{1}(\theta)}^{h_{2}(\theta)} \int_{u_{1}(r\cos(\theta), r\sin(\theta))}^{u_{2}(r\cos(\theta), r\sin(\theta))} f(r\cos(\theta), r\sin(\theta), z) r \; dz \; dr \; d\theta$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 다중적분의 변수변환법 (0) | 2022.07.11 |
|---|---|
| 미적분학 - 구좌표계에서의 삼중적분 (1) | 2022.07.05 |
| 미적분학 - 삼중적분 (0) | 2022.06.24 |
| 미적분학 - 극좌표계에서의 이중적분 (0) | 2022.06.22 |
| 미적분학 - 일반적인 영역에 대한 이중적분 정의 (0) | 2022.06.21 |
