안녕하세요. 지난 포스팅의 미적분학 - 극좌표에서의 이중적분에서는 극좌표에서 이중적분을 하는 방법에 대해서 알아보았습니다. 기본적인 원래는 기존의 이중적분과 동일하게 적분하려는 영역을 아주 작게 등분하는 것으로 시작하였습니다. 다만, 직교좌표계에서는 $x$축과 $y$-축을 기준으로 등분했지만, 극좌표계에서는 $r$과 $\thea$를 기준으로 등분하였습니다. 이때, $r = \sqrt{x^{2}+ y^{2}}$이고 $\theta = \arctan\left(\frac{y}{x}\right)$로 정의가 되었습니다. 오늘은 이어서 3개의 변수를 가진 함수 $w = f(x, y, z)$가 있을 때 적분하는 방법인 삼중적분에 대해서 알아보도록 하겠습니다.
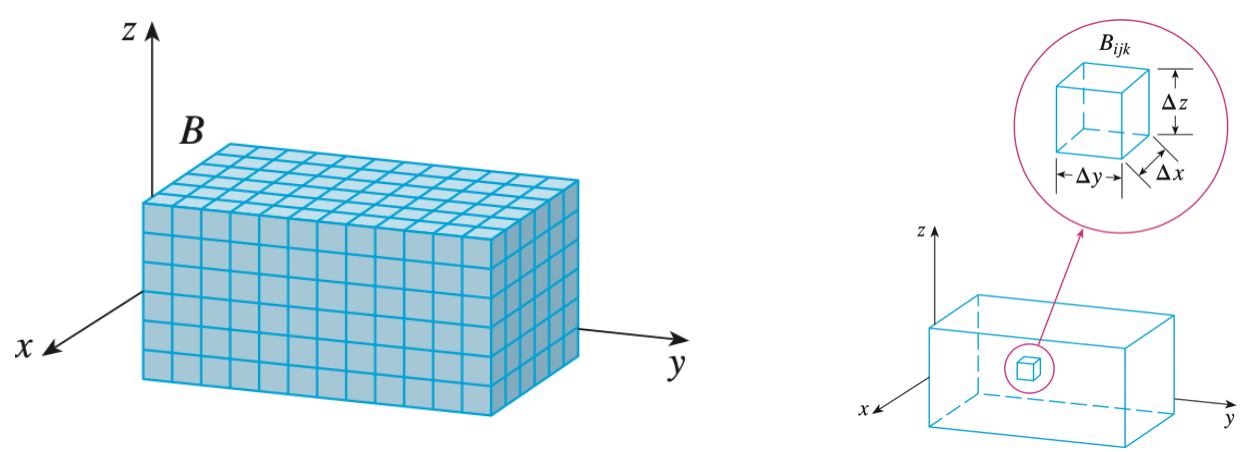
삼중적분의 기본적인 원리는 이중적분과 동일합니다. 이중적분에서는 함수가 $(x, y)$에 대한 변수이기 때문에 넓이에 대한 차분 $\Delta A$을 구하게되디만, 삼중적분에서는 함수가 $(x, y, z)$에 대한 변수이기 때문에 부피에 대한 차분 $\Delta V$를 구해야합니다. 이를 위해서는 어디를 적분할 지 영역을 먼저 정의해야겠죠. 이를 $B$라고 하겠습니다.
$$B = \{(x, y, z) | a \le x \le b, c \le y \le d, r \le z \le s\}$$
그리고 각 구간을 $l$등분, $m$등분, $n$등분한다고 가정하면 $x$축의 $i$번째 구간은 $[x_{i - 1}, x_{i}]$이고 $y$축의 $j$번째 구간은 $[y_{j - 1}, y_{j}]$, $z$축의 $k$번째 구간은 $[z_{k - 1}, z_{k}]$가 됩니다. 따라서, 각 변수의 구간으로 이루어진 작은 구간의영역 $B_{ijk}$를 정의할 수 있습니다.
$$B_{ijk} = [x_{i - 1}, x_{i}] \times [y_{j - 1}, y_{j}] \times [z_{k - 1}, z_{k}]$$
그리고 위의 오른쪽 그림과 같이 해당 영역 $B_{ijk}$의 부피의 차분은 각 구간의 등길이이므로 $\Delta V = \Delta x \Delta y \Delta z$입니다. 따라서, 저희는 각 구간의 삼중 리만 합(triple Riemann Sum)을 계산할 수 있습니다.
$$\sum_{i = 1}^{l} \sum_{j = 1}^{m} \sum_{k = 1}^{n} f(x_{ijk}^{*}, y_{ijk}^{*}, z_{ijk}^{*}) \Delta V$$
이때, $(x_{ijk}^{*}, y_{ijk}^{*}, z_{ijk}^{*})$를 각 영역 $B_{ijk}$의 표본점이라고 정의하겠습니다. 이제 실제 적분값을 구하기 위해서는 더 많이 쪼개면 되겠죠. 따라서, $l, m, n$을 무한으로 극한을 취해주면 됩니다.
$$\int \int \int_{B} f(x, y, z) \; dV = \lim_{l, m, n \rightarrow \infty} \sum_{i = 1}^{l} \sum_{j = 1}^{m} \sum_{k = 1}^{n} f(x_{ijk}^{*}, y_{ijk}^{*}, z_{ijk}^{*}) \Delta V$$
정리1. 삼중적분에 대한 푸비니의 정리(Fubini's Theorem for Triple Integrals)
함수 $f(x, y, z)$가 직육면체 $B = [a, b] \times [c, d] \times [r, s]$에서 연속이라고 하면 아래의 식이 성립한다.
$$\int \int \int_{B} f(x, y, z) dV = \int_{r}^{s} \int_{c}^{d} \int_{a}^{b} f(x, y, z) \; dx \; dy \; dz$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 구좌표계에서의 삼중적분 (0) | 2022.07.05 |
|---|---|
| 미적분학 - 원기둥좌표계에서 삼중적분 (0) | 2022.07.02 |
| 미적분학 - 극좌표계에서의 이중적분 (0) | 2022.06.22 |
| 미적분학 - 일반적인 영역에 대한 이중적분 정의 (0) | 2022.06.21 |
| 미적분학 - 반복적분 (0) | 2022.06.19 |
안녕하세요. 지난 포스팅의 미적분학 - 극좌표에서의 이중적분에서는 극좌표에서 이중적분을 하는 방법에 대해서 알아보았습니다. 기본적인 원래는 기존의 이중적분과 동일하게 적분하려는 영역을 아주 작게 등분하는 것으로 시작하였습니다. 다만, 직교좌표계에서는 x축과 y-축을 기준으로 등분했지만, 극좌표계에서는 r과 \thea를 기준으로 등분하였습니다. 이때, r=√x2+y2이고 θ=arctan(yx)로 정의가 되었습니다. 오늘은 이어서 3개의 변수를 가진 함수 w=f(x,y,z)가 있을 때 적분하는 방법인 삼중적분에 대해서 알아보도록 하겠습니다.

삼중적분의 기본적인 원리는 이중적분과 동일합니다. 이중적분에서는 함수가 (x,y)에 대한 변수이기 때문에 넓이에 대한 차분 ΔA을 구하게되디만, 삼중적분에서는 함수가 (x,y,z)에 대한 변수이기 때문에 부피에 대한 차분 ΔV를 구해야합니다. 이를 위해서는 어디를 적분할 지 영역을 먼저 정의해야겠죠. 이를 B라고 하겠습니다.
B={(x,y,z)|a≤x≤b,c≤y≤d,r≤z≤s}
그리고 각 구간을 l등분, m등분, n등분한다고 가정하면 x축의 i번째 구간은 [xi−1,xi]이고 y축의 j번째 구간은 [yj−1,yj], z축의 k번째 구간은 [zk−1,zk]가 됩니다. 따라서, 각 변수의 구간으로 이루어진 작은 구간의영역 Bijk를 정의할 수 있습니다.
Bijk=[xi−1,xi]×[yj−1,yj]×[zk−1,zk]
그리고 위의 오른쪽 그림과 같이 해당 영역 Bijk의 부피의 차분은 각 구간의 등길이이므로 ΔV=ΔxΔyΔz입니다. 따라서, 저희는 각 구간의 삼중 리만 합(triple Riemann Sum)을 계산할 수 있습니다.
l∑i=1m∑j=1n∑k=1f(x∗ijk,y∗ijk,z∗ijk)ΔV
이때, (x∗ijk,y∗ijk,z∗ijk)를 각 영역 Bijk의 표본점이라고 정의하겠습니다. 이제 실제 적분값을 구하기 위해서는 더 많이 쪼개면 되겠죠. 따라서, l,m,n을 무한으로 극한을 취해주면 됩니다.
∫∫∫Bf(x,y,z)dV=liml,m,n→∞l∑i=1m∑j=1n∑k=1f(x∗ijk,y∗ijk,z∗ijk)ΔV
정리1. 삼중적분에 대한 푸비니의 정리(Fubini's Theorem for Triple Integrals)
함수 f(x,y,z)가 직육면체 B=[a,b]×[c,d]×[r,s]에서 연속이라고 하면 아래의 식이 성립한다.
∫∫∫Bf(x,y,z)dV=∫sr∫dc∫baf(x,y,z)dxdydz
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 구좌표계에서의 삼중적분 (0) | 2022.07.05 |
|---|---|
| 미적분학 - 원기둥좌표계에서 삼중적분 (0) | 2022.07.02 |
| 미적분학 - 극좌표계에서의 이중적분 (0) | 2022.06.22 |
| 미적분학 - 일반적인 영역에 대한 이중적분 정의 (0) | 2022.06.21 |
| 미적분학 - 반복적분 (0) | 2022.06.19 |
