안녕하세요. 지난 포스팅의 미적분학 - 반복적분에서는 실질적으로 다변수 함수의 적분을 하는 방법에 대해서 알아보았습니다. 지금까지 저희는 직사각형 영역에 대한 이중적분을 해보았습니다. 오늘은 영역을 직사각형에 국한하지 않고 보다 일반적인 영역에서 이중적분을 수행하는 방법에 대해서 알아보도록 하겠습니다.
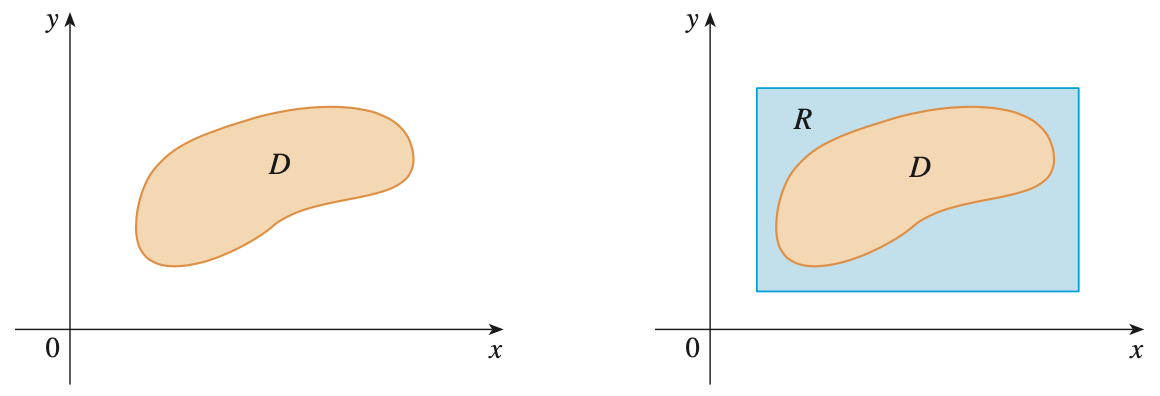
저희의 목표는 위의 왼쪽 그림과 같은 임의의 모양을 가진 영역 $D$ 상에서 이중적분을 하는 것이 목표입니다. 하지만, 기본적으로 저희는 현재 직사각형 영역에 대한 이중적분밖에 하지 못하기 때문에 이를 활용해야합니다. 따라서 오른쪽 그림과 같이 영역 $D$를 둘러싸는 새로운 직사각형 영역 $R$을 생각해보겠습니다. 그리고 기존의 함수를 $f$라고 했을 때 영역 $D$에서는 값을 그대로 같지만 영역 $D$ 밖, 그리고 직사각형 영역 $R$의 내부는 0으로 하는 새로운 함수 $F$를 정의하겠습니다.
$$F(x, y) = \begin{cases} f(x, y) &\text{ if } (x, y) \in D \\ 0 &\text{ if } (x, y) \notin D \text{ and } (x, y) \in R\end{cases}$$
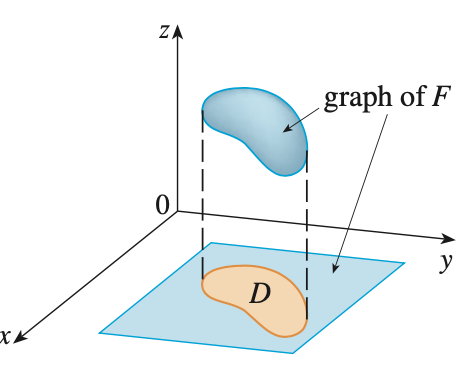
위와 같이 정의하면 영역 $D$의 바깥의 영역에 대한 함수 $F$의 값은 0이 됩니다. 이제 직사각형 영역 $R$에 대해서 함수 $F$를 적분하게 되면 $D$ 바깥의 영역에 대한 함수값은 0이기 때문에 저희는 영역 $D$에서의 함수값을 쉽게 구할 수 있습니다.
$$\int\int_{D} f(x, y) \; dA = \int\int_{R} F(x, y) \; dA$$
이제부터 저희는 영역 $D$의 모양에 따라 2가지 타입으로 나누고 각각에 대한 적분을 실제로 계산하는 방법에 대해서 알아보도록 하겠습니다.
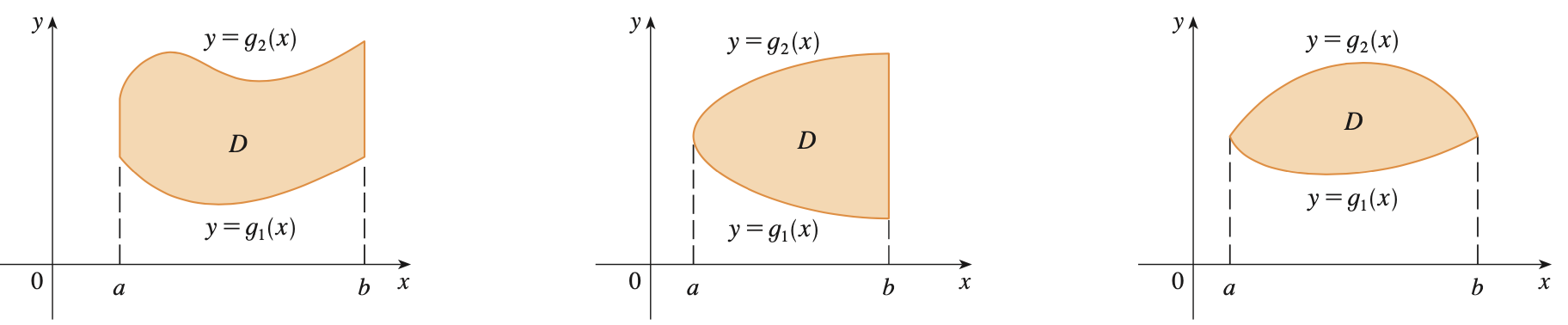
첫번째 타입의 모양입니다. 이 타입의 경우에는 $x = a$ 그리고 $x = b$로 고정되어 있기 때문에 직사각형 영역 $R$의 $x$축에 대한 범위를 정의할 때는 $[a, b]$로 정의하면 됩니다. 다음 문제는 $y$축 범위입니다. 일단, 첫번째로 할 일은 위 영역을 둘러싸는 직사각형 영역 $R$을 정의해보겠습니다.
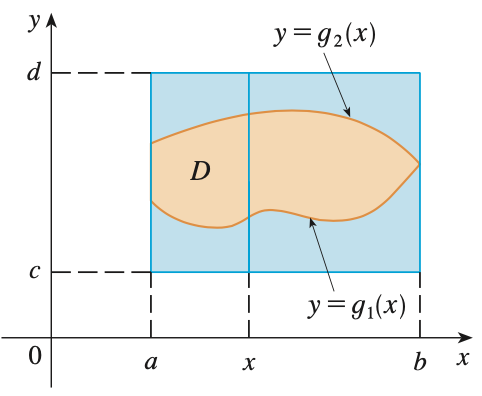
잘 보시면 직사각형 영역 $R = [a, b] \times [c, d]$로 정의되는 것을 볼 수 있습니다. 따라서, 영역 $D$에 대한 함수 $f$의 적분은 아래와 같이 하면 됩니다.
$$\int\int_{D} f(x, y) \; dA = \int\int_{R} F(x, y) \; dA = \int_{a}^{b} \int_{c}^{d} F(x, y) \; dx \; dy$$
그런데 여기서 $y < g_{1}(x)$이고 $y > g_{2}(x)$인 영역에서는 영역 $D$의 바깥영역이기 때문에 $F(x, y) = 0$가 됩니다. 따라서, 저희는 최종적으로 이 영역에 대한 이중적분을 어떻게 할 지 알 수 있습니다.
정리1.
함수 $f$가 1번 타입의 영역 $D = \{(x, y) \in \mathbb{R}^{2} | a \le x \le b \text{ and } g_{1}(x) \le y \le g_{2}(x)\}$에서 연속이면 영역 $D$에서 함수 $f$의 적분은 아래와 같다.
$$\int\int_{D} f(x, y) \; dA = \int_{a}^{b} \int_{g_{1}(x)}^{g_{2}(x)} f(x, y) \; dy \; dx$$
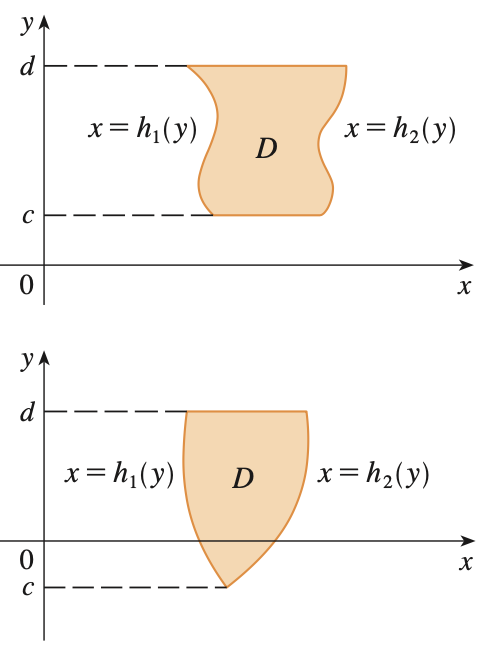
다음으로 고려해볼 모양의 영역은 위 그림과 같습니다. 1번 타입 모양과 비교해보면 이번에는 $y$축의 값이 $y = c$와 $y = d$로 고정되어 있습니다. 이 경우에도 1번 타입과 동일하게 직사각형 영역을 만들어주고 적분을 하면 됩니다. 다만 다른점은 $x$축이 값이 변하기 때문에 아래와 같이 적분을 해야하죠.
정리2.
함수 $f$가 2번 타입의 영역 $D = \{(x, y) \in \mathbb{R}^{2} | h_{1}(y) \le x \le h_{2}(y) \text{ and } c \le y \le d\}$에서 연속이면 영역 $D$에서 함수 $f$의 적분은 아래와 같다.
$$\int\int_{D} f(x, y) \; dA = \int_{c}^{d} \int_{h_{1}(y)}^{h_{2}(y)} f(x, y) \; dx \; dy$$
정리3. 이중적분의 성질(Properties of Double Integrals)
함수 $f$와 $g$가 임의의 영역 $D$에서 연속이라고 하자. 여기서 $c$는 임의의 상수이다.
- $\int\int_{D} \left[f(x, y) + g(x, y) \right] \; dA = \int\int_{D} f(x, y) \; dA + \int\int_{D} g(x, y) \; dA$
- $\int\int_{D} cf(x, y) \; dA = c\int\int_{D} f(x, y) \; dA$
- 영역 $D$에서 $f(x) \ge g(x)$를 만족하면 $\int\int_{D} f(x, y) \; dA \le \int\int_{D} g(x, y) \; dA$이다.
- 영역 $D$를 $D = D_{1} \cup D_{2}$와 $\emptyset = D_{1} \cap D_{2}$를 만족하는 두 개의 영역 $D_{1}$과 $D_{2}$로 나누어진다고 할 때 아래의 식을 만족한다.
$$\int\int_{D} f(x, y) \; dA = \int\int_{D_{1}} f(x, y) \; dA + \int\int_{D_{2}} f(x, y) \; dA$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 삼중적분 (0) | 2022.06.24 |
|---|---|
| 미적분학 - 극좌표계에서의 이중적분 (0) | 2022.06.22 |
| 미적분학 - 반복적분 (0) | 2022.06.19 |
| 미적분학 - 이중적분 (0) | 2022.06.18 |
| 미적분학 - 라그랑주 승수법 (1) | 2022.06.18 |
