안녕하세요. 지난 포스팅의 집합론 - 대우, 역, 그리고 부정에서는 명제의 대우, 역 그리고 부정을 구하는 방법에 대해서 알아보았습니다. 이때, 명제의 참/거짓을 증명하기 어려울 때 사용하는 방법이 대우명제를 통한 간접증명임도 설명하였습니다. 오늘은 차집합과 집합론과 관련된 몇 가지 규칙들을 설명드리도록 하겠습니다.
정의1. 차집합(Difference of two sets)
임의의 두 집합 $A$와 $B$가 주어졌을 때 $A$와 $B$의 차집합은 $A - B = \{x | x \in A \text{ and } x \notin B\}$이다.
설명
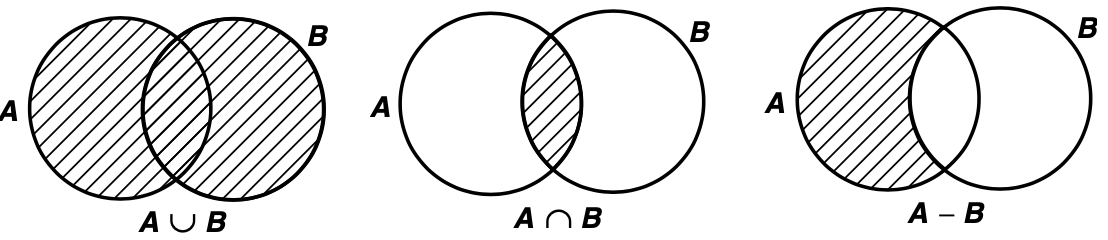
지금까지 저희는 두 개의 집합에 대한 3가지 연산(합집합, 교집합, 차집합)에 대해서 알아보았습니다. 그리고 각 연산 결과를 벤다이어그램으로 그려보면 위와 같은 그림을 얻을 수 있습니다. 특히, 차집합 같은 경우에는 집합 $A$에는 속하지만 집합 $B$에는 속하지 않는 집합을 의미하기 때문에 집합 $A$에서 $A \cap B$가 빠진것을 볼 수 있습니다. 일반적으로 합집합과 교집합과 다르게 차집합은 교환법칙이 성립되지 않습니다. 즉, $A - B \neq B - A$임을 쉽게 아실 수 있을겁니다. 이때, 집합 $A$와 집합 $B$의 차집합을 집합 $A$에 대한 집합 $B$의 여집합(complement)라고도 합니다.
정리1. 분배법칙(Distributive Law)
임의의 세 집합 $A, B, C$에 대해 1. $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$, 2. $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$이 성립한다.
증명(정리1)
1. $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
집합 $A \cap (B \cup C)$에서 임의의 원소 $x$를 선택한다.
$$\begin{align*} x \in A \cap (B \cup C) &\iff x \in A \text{ and } x \in B \cup C \because \text{ 교집합 정의} \\ &\iff x \in A \text{ and } \left(x \in B \text{ or } x \in C \right) \because \text{ 합집합 정의} \\ &\iff \left(x \in A \text{ and } x \in B \right) \text{ or } \left(x \in A \text{ and } x \in C\right) \\ &\iff x \in (A \cap B) \cup (A \cap C) \end{align*}$$
임의의 원소 $x$가 $(A \cap B) \cup (A \cap C)$에도 속하기 때문에 $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$이다.
2. $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
집합 $A \cup (B \cap C)$에서 임의의 원소 $x$를 선택한다.
$$\begin{align*} x \in A \cup (B \cap C) &\iff x \in A \text{ or } x \in B \cap C \because \text{ 합집합 정의} \\ &\iff x \in A \text{ or } \left(x \in B \text{ and } x \in C \right) \because \text{ 교집합 정의} \\ &\iff \left(x \in A \text{ or } x \in B \right) \text{ and } \left(x \in A \text{ or } x \in C\right) \\ &\iff x \in (A \cup B) \cap (A \cup C) \end{align*}$$
임의의 원소 $x$가 $(A \cup B) \cap (A \cup C)$에도 속하기 때문에 $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$이다.
정리2. 드모르간의 법칙(DeMorgan's Law)
임의의 세 집합 $A, B, C$에 대해 1. $A - (B \cup C) = (A - B) \cap (A - C)$, 2. $A - (B \cap C) = (A - B) \cup (A - C)$이 성립한다.
증명(정리2)
1. $A - (B \cup C) = (A - B) \cup (A - C)$
집합 $A - (B \cup C)$에서 임의의 원소 $x$를 선택한다.
$$\begin{align*} x \in A - (B \cup C) &\iff x \in A \text{ and } x \notin B \cup C \because \text{ 차집합 정의} \\ &\iff x \in A \text{ and } \left(x \notin B \text{ and } x \notin C \right) \because \text{ 합집합 정의와 명제 부정 조합} \\ &\iff \left(x \in A \text{ and } x \notin B \right) \text{ and } \left(x \in A \text{ and } x \notin C\right) \\ &\iff x \in (A - B) \cap (A - C) \end{align*}$$
임의의 원소 $x$가 $(A - B) \cap (A - C)$에도 속하기 때문에 $A - (B \cup C) = (A - B) \cap (A - C)$이다.
2. $A - (B \cap C) = (A - B) \cup (A - C)$
집합 $A - (B \cap C)$에서 임의의 원소 $x$를 선택한다.
$$\begin{align*} x \in A - (B \cap C) &\iff x \in A \text{ and } x \notin B \cap C \because \text{ 차집합 정의} \\ &\iff x \in A \text{ and } \left(x \notin B \text{ or } x \notin C \right) \because \text{ 교집합 정의와 명제 부정 조합} \\ &\iff \left(x \in A \text{ and } x \notin B \right) \text{ or } \left(x \in A \text{ and } x \notin C\right) \\ &\iff x \in (A - B) \cup (A - C) \end{align*}$$
임의의 원소 $x$가 $(A - B) \cup (A - C)$에도 속하기 때문에 $A - (B \cap C) = (A - B) \cup (A - C)$이다.
드모르간의 법칙을 쉽게 이해하는 방법은 아래와 같습니다.
- 합집합의 여집합은 여집합의 교집합과 동일하다.
- 교집합의 여집합은 여집합의 합집합과 동일하다.
참고자료 및 그림출처
Topology(James Munkres) Ch1. Fundamental Concepts
'수학 > 집합론' 카테고리의 다른 글
| 집합론 - 데카르트 곱 (0) | 2022.07.04 |
|---|---|
| 집합론 - 확장된 합집합과 교집합 (0) | 2022.06.25 |
| 집합론 - 대우, 역, 그리고 부정 (0) | 2022.06.20 |
| 집합론 - 교집합, 공집합, "If ... Then"의 의미 (0) | 2022.06.19 |
| 집합론 - "or"의 의미 (2) | 2022.06.18 |
안녕하세요. 지난 포스팅의 집합론 - 대우, 역, 그리고 부정에서는 명제의 대우, 역 그리고 부정을 구하는 방법에 대해서 알아보았습니다. 이때, 명제의 참/거짓을 증명하기 어려울 때 사용하는 방법이 대우명제를 통한 간접증명임도 설명하였습니다. 오늘은 차집합과 집합론과 관련된 몇 가지 규칙들을 설명드리도록 하겠습니다.
정의1. 차집합(Difference of two sets)
임의의 두 집합 $A$와 $B$가 주어졌을 때 $A$와 $B$의 차집합은 $A - B = \{x | x \in A \text{ and } x \notin B\}$이다.
설명

지금까지 저희는 두 개의 집합에 대한 3가지 연산(합집합, 교집합, 차집합)에 대해서 알아보았습니다. 그리고 각 연산 결과를 벤다이어그램으로 그려보면 위와 같은 그림을 얻을 수 있습니다. 특히, 차집합 같은 경우에는 집합 $A$에는 속하지만 집합 $B$에는 속하지 않는 집합을 의미하기 때문에 집합 $A$에서 $A \cap B$가 빠진것을 볼 수 있습니다. 일반적으로 합집합과 교집합과 다르게 차집합은 교환법칙이 성립되지 않습니다. 즉, $A - B \neq B - A$임을 쉽게 아실 수 있을겁니다. 이때, 집합 $A$와 집합 $B$의 차집합을 집합 $A$에 대한 집합 $B$의 여집합(complement)라고도 합니다.
정리1. 분배법칙(Distributive Law)
임의의 세 집합 $A, B, C$에 대해 1. $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$, 2. $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$이 성립한다.
증명(정리1)
1. $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
집합 $A \cap (B \cup C)$에서 임의의 원소 $x$를 선택한다.
$$\begin{align*} x \in A \cap (B \cup C) &\iff x \in A \text{ and } x \in B \cup C \because \text{ 교집합 정의} \\ &\iff x \in A \text{ and } \left(x \in B \text{ or } x \in C \right) \because \text{ 합집합 정의} \\ &\iff \left(x \in A \text{ and } x \in B \right) \text{ or } \left(x \in A \text{ and } x \in C\right) \\ &\iff x \in (A \cap B) \cup (A \cap C) \end{align*}$$
임의의 원소 $x$가 $(A \cap B) \cup (A \cap C)$에도 속하기 때문에 $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$이다.
2. $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
집합 $A \cup (B \cap C)$에서 임의의 원소 $x$를 선택한다.
$$\begin{align*} x \in A \cup (B \cap C) &\iff x \in A \text{ or } x \in B \cap C \because \text{ 합집합 정의} \\ &\iff x \in A \text{ or } \left(x \in B \text{ and } x \in C \right) \because \text{ 교집합 정의} \\ &\iff \left(x \in A \text{ or } x \in B \right) \text{ and } \left(x \in A \text{ or } x \in C\right) \\ &\iff x \in (A \cup B) \cap (A \cup C) \end{align*}$$
임의의 원소 $x$가 $(A \cup B) \cap (A \cup C)$에도 속하기 때문에 $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$이다.
정리2. 드모르간의 법칙(DeMorgan's Law)
임의의 세 집합 $A, B, C$에 대해 1. $A - (B \cup C) = (A - B) \cap (A - C)$, 2. $A - (B \cap C) = (A - B) \cup (A - C)$이 성립한다.
증명(정리2)
1. $A - (B \cup C) = (A - B) \cup (A - C)$
집합 $A - (B \cup C)$에서 임의의 원소 $x$를 선택한다.
$$\begin{align*} x \in A - (B \cup C) &\iff x \in A \text{ and } x \notin B \cup C \because \text{ 차집합 정의} \\ &\iff x \in A \text{ and } \left(x \notin B \text{ and } x \notin C \right) \because \text{ 합집합 정의와 명제 부정 조합} \\ &\iff \left(x \in A \text{ and } x \notin B \right) \text{ and } \left(x \in A \text{ and } x \notin C\right) \\ &\iff x \in (A - B) \cap (A - C) \end{align*}$$
임의의 원소 $x$가 $(A - B) \cap (A - C)$에도 속하기 때문에 $A - (B \cup C) = (A - B) \cap (A - C)$이다.
2. $A - (B \cap C) = (A - B) \cup (A - C)$
집합 $A - (B \cap C)$에서 임의의 원소 $x$를 선택한다.
$$\begin{align*} x \in A - (B \cap C) &\iff x \in A \text{ and } x \notin B \cap C \because \text{ 차집합 정의} \\ &\iff x \in A \text{ and } \left(x \notin B \text{ or } x \notin C \right) \because \text{ 교집합 정의와 명제 부정 조합} \\ &\iff \left(x \in A \text{ and } x \notin B \right) \text{ or } \left(x \in A \text{ and } x \notin C\right) \\ &\iff x \in (A - B) \cup (A - C) \end{align*}$$
임의의 원소 $x$가 $(A - B) \cup (A - C)$에도 속하기 때문에 $A - (B \cap C) = (A - B) \cup (A - C)$이다.
드모르간의 법칙을 쉽게 이해하는 방법은 아래와 같습니다.
- 합집합의 여집합은 여집합의 교집합과 동일하다.
- 교집합의 여집합은 여집합의 합집합과 동일하다.
참고자료 및 그림출처
Topology(James Munkres) Ch1. Fundamental Concepts
'수학 > 집합론' 카테고리의 다른 글
| 집합론 - 데카르트 곱 (0) | 2022.07.04 |
|---|---|
| 집합론 - 확장된 합집합과 교집합 (0) | 2022.06.25 |
| 집합론 - 대우, 역, 그리고 부정 (0) | 2022.06.20 |
| 집합론 - 교집합, 공집합, "If ... Then"의 의미 (0) | 2022.06.19 |
| 집합론 - "or"의 의미 (2) | 2022.06.18 |
