안녕하세요. 지난 포스팅의 미적분학 - 다변수 함수의 최대최소에서는 다변수 함수가 정의된 정의역 내에서 최댓값과 최솟값을 구하는 방법에 대해서 알아보았습니다. 오늘은 다변수 함수와 함께 특별한 제약조건(constraint)이 포함되었을 때 다변수 함수의 최댓값과 최솟값을 구하는 방법인 라그랑주 승수법(Method of Lagrange Multiplier)에 대해서 알아보도록 하겠습니다.
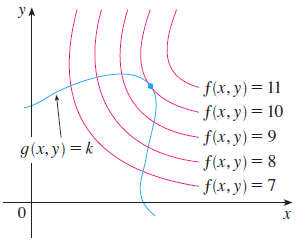
라그랑주 승수법의 기본 개념을 이해하기 위해 위 그림을 함께 설명하도록 하겠습니다. 여기서 $y = f(x, y)$의 다변수 함수가 주어졌다고 가정하겠습니다. 그리고 $f(x, y) = C$로 이어진 분홍선 선 그래프는 함수 $y = f(x, y)$의 등고선을 의미합니다. 이제부터 저희가 원하는 것은 $g(x, y) = k$라는 제약 조건 하에서 함수 $y = f(x, y)$의 극값(extreme value)를 찾는 것입니다. 즉, 저희는 함수 $y = f(x, y)$와 $g(x, y) = k$와 서로 만나면서 최대가 되는 값을 찾아야하죠. 위 그림에서 $C = 7, 8, 9$일 때는 $g(x, y) = k$와 만나기는 하지만 최대는 아니죠. 그와 반면에 $C = 11$일 때는 $g(x, y) = k$와 만나지도 못합니다. 따라서, 이 경우에 극값은 $C = 11$이 되는 것이죠. 그리고 그 점은 위 그림에서 파란색 점으로 표시되어 있습니다. 이 점을 $(x_{0}, y_{0})$라고 하겠습니다. 이때, 이 점에서 두 함수 $f$와 $g$의 기울기벡터가 평행한 것을 볼 수 있죠. 따라서, 이에 대한 새로운 방정식을 쓸 수 있습니다.
$$\nabla f(x_{0}, y_{0}) = \lambda \nabla g(x_{0}, y_{0})$$
여기서 $\lambda$를 앞으로 라그랑주 승수(Lagrange Multiplier)이라고 하겠습니다.
정리1. 라그랑주 승수법(Method of Lagrange Multiplier) - 1
함수 $f(x, y, z)$와 제약조건 $g(x, y, z) = k$가 주어졌을 때 함수 $f$의 최댓값 또는 최솟값은 아래의 과정을 통해 구할 수 있다.
STEP1. $\nabla f(x, y, z) = \lambda \nabla g(x, y, z)$와 $g(x, y, z) = k$를 동시에 만족하는 모든 $x, y, z$ 그리고 $\lambda$를 찾는다.
STEP2. STEP1에서 얻은 모든 순서쌍 $(x, y, z)$을 함수 $f$에 대입하여 값을 비교했을 때 가장 큰 값이 최댓값이고 작은 값이 최솟값이다.
예제1. 함수 $f(x, y) = x^{2} + 2y^{2}$와 제약조건 $x^{2} + y^{2} = 1$ 하에서 함수 $f$의 극값을 구하여라.
STEP1. $\nabla f(x, y, z) = \lambda \nabla g(x, y, z)$와 $g(x, y, z) = k$를 동시에 만족하는 모든 $x, y, z$ 그리고 $\lambda$를 찾는다.
1). $\nabla f(x, y) = \lambda \nabla g(x, y) \Rightarrow <2x, 4y> = \lambda <2x, 2y>$와 $g(x, y) = x^{2} + y^{2} - 1$
$$\begin{cases} x = \lambda x &\text{ (1) } \\ 2y = \lambda y &\text{ (2) }\\ x^{2} + y^{2} = 1 &\text{ (3) } \end{cases}$$
(1)번 식으로부터 $x = 0$ 또는 $x \neq 0$ 일 때, $\lambda = 1$임을 알 수 있다.
1). $x = 0$이라고 하자. 그러면 (3)번 식으로부터 $y = \pm 1$임을 알 수 있다. 따라서, $(0, 1)$과 $(0, -1)$이다.
2). $\lambda = 1$이라고 하자. 그러면 (2)번 식은 $2y = y$가 되고 이는 $y = 0$임을 알 수 있다. 이를 (3)번 식에 대입하면 $x = \pm 1$임을 알 수 있다. 따라서, $(1, 0)$과 $(-1, 0)$이다.
따라서, 얻은 모든 점은 $(0, 1), (0, -1), (1, 0), (-1, 0)$이다.
STEP2. STEP1에서 얻은 모든 순서쌍 $(x, y, z)$을 함수 $f$에 대입하여 값을 비교했을 때 가장 큰 값이 최댓값이고 작은 값이 최솟값이다.
1). $f(0, 1) = 0^{2} + 2 \cdot 1^{2} = 2$
2). $f(0, -1) = 0^{2} + 2 \cdot (-1)^{2} = 2$
3). $f(1, 0) = 1^{2} + 2 \cdot 0^{2} = 1$
4). $f(-1, 0) = (-1)^{2} + 2 \cdot 0^{2} = 1$
따라서, 함수 $f$의 최댓값은 점 $(0, 1)$과 $(0, -1)$에서 2가 되고 최솟값은 점 $(1, 0)$과 $(-1, 0)$에서 1이 된다.
정리2. 라그랑주 승수법(Method of Lagrange Multiplier) - 2
함수 $f(x, y, z)$와 두 개의 제약조건 $g(x, y, z) = k$와 $h(x, y, z) = c$가 주어졌을 때 함수 $f$의 최댓값 또는 최솟값은 아래의 과정을 통해 구할 수 있다.
STEP1. $\nabla f(x, y, z) = \lambda \nabla g(x, y, z) + \mu \nabla h(x, y, z)$와 $g(x, y, z) = k, h(x, y, z) = c$를 동시에 만족하는 모든 $x, y, z$ 그리고 $\lambda$와 $\mu$를 찾는다.
STEP2. STEP1에서 얻은 모든 순서쌍 $(x, y, z)$을 함수 $f$에 대입하여 값을 비교했을 때 가장 큰 값이 최댓값이고 작은 값이 최솟값이다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 반복적분 (0) | 2022.06.19 |
|---|---|
| 미적분학 - 이중적분 (0) | 2022.06.18 |
| 미적분학 - 다변수 함수의 최대최소 (1) | 2022.06.16 |
| 미적분학 - 기울기벡터 (0) | 2022.06.15 |
| 미적분학 - 방향미분 (0) | 2022.06.14 |
안녕하세요. 지난 포스팅의 미적분학 - 다변수 함수의 최대최소에서는 다변수 함수가 정의된 정의역 내에서 최댓값과 최솟값을 구하는 방법에 대해서 알아보았습니다. 오늘은 다변수 함수와 함께 특별한 제약조건(constraint)이 포함되었을 때 다변수 함수의 최댓값과 최솟값을 구하는 방법인 라그랑주 승수법(Method of Lagrange Multiplier)에 대해서 알아보도록 하겠습니다.

라그랑주 승수법의 기본 개념을 이해하기 위해 위 그림을 함께 설명하도록 하겠습니다. 여기서 y=f(x,y)의 다변수 함수가 주어졌다고 가정하겠습니다. 그리고 f(x,y)=C로 이어진 분홍선 선 그래프는 함수 y=f(x,y)의 등고선을 의미합니다. 이제부터 저희가 원하는 것은 g(x,y)=k라는 제약 조건 하에서 함수 y=f(x,y)의 극값(extreme value)를 찾는 것입니다. 즉, 저희는 함수 y=f(x,y)와 g(x,y)=k와 서로 만나면서 최대가 되는 값을 찾아야하죠. 위 그림에서 C=7,8,9일 때는 g(x,y)=k와 만나기는 하지만 최대는 아니죠. 그와 반면에 C=11일 때는 g(x,y)=k와 만나지도 못합니다. 따라서, 이 경우에 극값은 C=11이 되는 것이죠. 그리고 그 점은 위 그림에서 파란색 점으로 표시되어 있습니다. 이 점을 (x0,y0)라고 하겠습니다. 이때, 이 점에서 두 함수 f와 g의 기울기벡터가 평행한 것을 볼 수 있죠. 따라서, 이에 대한 새로운 방정식을 쓸 수 있습니다.
∇f(x0,y0)=λ∇g(x0,y0)
여기서 λ를 앞으로 라그랑주 승수(Lagrange Multiplier)이라고 하겠습니다.
정리1. 라그랑주 승수법(Method of Lagrange Multiplier) - 1
함수 f(x,y,z)와 제약조건 g(x,y,z)=k가 주어졌을 때 함수 f의 최댓값 또는 최솟값은 아래의 과정을 통해 구할 수 있다.
STEP1. ∇f(x,y,z)=λ∇g(x,y,z)와 g(x,y,z)=k를 동시에 만족하는 모든 x,y,z 그리고 λ를 찾는다.
STEP2. STEP1에서 얻은 모든 순서쌍 (x,y,z)을 함수 f에 대입하여 값을 비교했을 때 가장 큰 값이 최댓값이고 작은 값이 최솟값이다.
예제1. 함수 f(x,y)=x2+2y2와 제약조건 x2+y2=1 하에서 함수 f의 극값을 구하여라.
STEP1. ∇f(x,y,z)=λ∇g(x,y,z)와 g(x,y,z)=k를 동시에 만족하는 모든 x,y,z 그리고 λ를 찾는다.
1). ∇f(x,y)=λ∇g(x,y)⇒<2x,4y>=λ<2x,2y>와 g(x,y)=x2+y2−1
{x=λx (1) 2y=λy (2) x2+y2=1 (3)
(1)번 식으로부터 x=0 또는 x≠0 일 때, λ=1임을 알 수 있다.
1). x=0이라고 하자. 그러면 (3)번 식으로부터 y=±1임을 알 수 있다. 따라서, (0,1)과 (0,−1)이다.
2). λ=1이라고 하자. 그러면 (2)번 식은 2y=y가 되고 이는 y=0임을 알 수 있다. 이를 (3)번 식에 대입하면 x=±1임을 알 수 있다. 따라서, (1,0)과 (−1,0)이다.
따라서, 얻은 모든 점은 (0,1),(0,−1),(1,0),(−1,0)이다.
STEP2. STEP1에서 얻은 모든 순서쌍 (x,y,z)을 함수 f에 대입하여 값을 비교했을 때 가장 큰 값이 최댓값이고 작은 값이 최솟값이다.
1). f(0,1)=02+2⋅12=2
2). f(0,−1)=02+2⋅(−1)2=2
3). f(1,0)=12+2⋅02=1
4). f(−1,0)=(−1)2+2⋅02=1
따라서, 함수 f의 최댓값은 점 (0,1)과 (0,−1)에서 2가 되고 최솟값은 점 (1,0)과 (−1,0)에서 1이 된다.
정리2. 라그랑주 승수법(Method of Lagrange Multiplier) - 2
함수 f(x,y,z)와 두 개의 제약조건 g(x,y,z)=k와 h(x,y,z)=c가 주어졌을 때 함수 f의 최댓값 또는 최솟값은 아래의 과정을 통해 구할 수 있다.
STEP1. ∇f(x,y,z)=λ∇g(x,y,z)+μ∇h(x,y,z)와 g(x,y,z)=k,h(x,y,z)=c를 동시에 만족하는 모든 x,y,z 그리고 λ와 μ를 찾는다.
STEP2. STEP1에서 얻은 모든 순서쌍 (x,y,z)을 함수 f에 대입하여 값을 비교했을 때 가장 큰 값이 최댓값이고 작은 값이 최솟값이다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 반복적분 (0) | 2022.06.19 |
|---|---|
| 미적분학 - 이중적분 (0) | 2022.06.18 |
| 미적분학 - 다변수 함수의 최대최소 (1) | 2022.06.16 |
| 미적분학 - 기울기벡터 (0) | 2022.06.15 |
| 미적분학 - 방향미분 (0) | 2022.06.14 |
