안녕하세요. 지난 포스팅의 미적분학 - 3차원 직선과 평면의 방정식에서는 3차원에서 벡터를 이용하여 직선과 평면을 표현하는 벡터 방정식(vector equation)과 스칼라로 풀어서 표현하는 직선을 위한 대칭 방정식(symmetric equation)과 스칼라 방정식(scalar equation)에 대해서 알아보았습니다. 오늘은 두 평면이 교차하는 직선을 구하는 방법과 평행하는 평면과 점 사이의 거리를 구하는 방법에 대해서 알아보겠습니다.

일단, 몸풀기로 간단한 문제부터 생각해보겠습니다. 위와 같이 두 평면이 교차할 때 이루는 각 $\theta$을 어떻게 구할 수 있을까요? 방법은 간단합니다. 기본적으로 두 개의 평면 모두 법선벡터 $\mathbf{n}_{1}$과 $\mathbf{n}_{2}$를 가지고 있습니다. 따라서, 위 그림과 같이 두 벡터 사이의 각도를 구하면 평면 사이의 각도를 구할 수 있죠.
$$\theta = \arccos\left(\frac{\mathbf{n}_{1} \cdot \mathbf{n}_{2}}{|\mathbf{n}_{1}||\mathbf{n}_{2}|}\right)$$
예제1. 두 평면 $x + y + z = 1$과 $x - 2y + 3z = 1$ 이 이루는 각도를 구하여라.
첫번째 평면의 법선벡터는 $\mathbf{n}_{1} = <1, 1, 1>$이고 두번째 평면의 법선벡터는 $\mathbf{n}_{2} = <1, -2, 3>$이다. 따라서, 두 평면이 이루는 각은 아래와 같다.
$$\theta = \arccos\left(\frac{<1, 1, 1> \cdot <1, -2, 3>}{|<1, 1, 1>||<1, -2, 3>|}\right) = \arccos\left(\frac{2}{\sqrt{42}}\right)$$
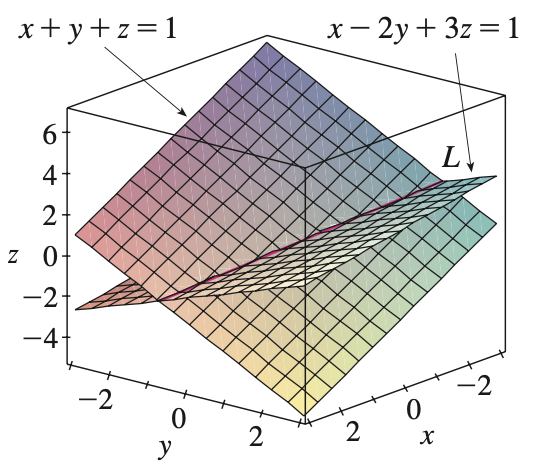
그렇다면 본론으로 들어와서 두 평면이 교차할 때 이루는 직선은 어떻게 구할 수 있을까요? 이 역시 간단합니다. 일단 직선을 구하기 위해서는 직선이 지나는 한점과 방향벡터를 필요로 합니다. 이때, 직선이 지나는 점은 쉽게 구할 수 있습니다. $x, y, z$ 중 하나의 변수를 0이라고 둔 뒤 연립방정식을 풀면 됩니다. 예를 들어서 두 평면 $x + y + z = 1$과 $x - 2y + 3z = 1$이 있다고 가정했을 때, $z= 0 $이라고 두겠습니다.
$$\begin{cases} x + y = 1 \\ x - 2y = 1\end{cases} \Rightarrow x = 1, y = 0$$
위와 같이 연립방정식을 풀어서 직선이 지나는 점을 구할 수 있습니다. 이때, 어떤 변수를 0으로 두냐는 문제마다 다르기 때문에 문제를 풀기 쉬운대로 하시면 됩니다. 다음으로 방향벡터를 구해보겠습니다. 잘 관찰해보시면 직선의 방향벡터는 항상 두 평면의 법선벡터와 수직임을 알 수 있습니다. 따라서, 미적분학 - 벡터의 외적에서 보았듯이 두 벡터의 외적을 통해서 직선의 방향벡터를 구할 수 있습니다.
$$\mathbf{v} = \mathbf{n}_{1} \times \mathbf{n}_{2} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 1 & 1 \\ 1 & -2 & 3 \end{vmatrix} = <5, -2, -3>$$
따라서, 두 평면이 교차하는 직선의 대칭방정식은 아래와 같습니다.
$$\frac{x - 1}{5} = \frac{y}{-2} = \frac{z}{-3} = t$$
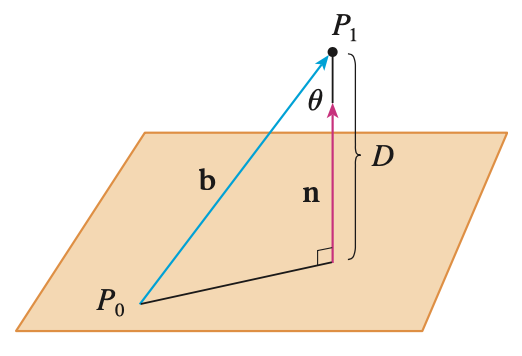
다음으로 점과 평면 사이의 최단 거리부터 구해보도록 하죠. 위 그림에서는 점 $P_{1}(x_{1}, y_{1}, z_{1})$와 평면 $ax + by + cz + d = 0$ 사이의 거리 $D$를 구해야합니다. 여기서 거리 $D$가 무엇인지 잘 생각해보도록 하죠. 미적분학 - 벡터의 방향각과 사영에서 보았던 $\text{comp}_{\mathbf{a}} \mathbf{b}$에 대한 개념을 숙지하셨다면 $D = \left|\text{comp}_{\mathbf{n}} \mathbf{b}\right|$임을 알 수 있습니다. 즉, 거리 $D$를 벡터 $\mathbf{b}$를 법선벡터 $\mathbf{n}$에 사영시켰을 때 거리로 생각하는 것입니다. 여기서, $\mathbf{b} = \vec{P_{0}P_{1}} = \vec{OP_{1}} - \vec{OP_{0}} = <x_{1} - x_{0}, y_{1} - y_{0}, z_{1} - z_{0}>$입니다.
$$\begin{align*} D &= \left|\text{comp}_{\mathbf{n}} \mathbf{b} \right| \\ &= \frac{|\mathbf{n} \cdot \mathbf{b}|}{|\mathbf{n}|} \\ &= \frac{\left|a(x_{1} - x_{0}) + b(y_{1} - y_{0}) + c(z_{1} - z_{0})\right|}{\sqrt{a^{2} + b^{2} + c^{2}}} \\ &= \frac{\left|(ax_{1} + by_{1} + cz_{1}) - (ax_{0} + by_{0} + cz_{0})\right|}{\sqrt{a^{2} + b^{2} + c^{2}}} \\ &= \frac{\left|ax_{1} + by_{1} + cz_{1}\right|}{\sqrt{a^{2} + b^{2} +c^{2}}} \end{align*}$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 벡터함수와 공간곡선 (0) | 2022.05.28 |
|---|---|
| 미적분학 - 3차원 원통과 이차곡면 (0) | 2022.05.27 |
| 미적분학 - 3차원 직선과 평면의 방정식 (0) | 2022.05.25 |
| 미적분학 - 벡터의 외적 (1) | 2022.05.24 |
| 미적분학 - 벡터의 방향각과 사영 (0) | 2022.05.22 |
