안녕하세요. 지난 포스팅의 미적분학 - 벡터의 외적에서는 두 벡터의 외적(outer product, cross product, vector product)을 계산하는 방법과 이와 관련된 다양한 정리들에 대해서 알아보았습니다. 오늘은 3차원 상에서 직선과 평면을 대수적으로 표현하는 방법에 대해서 알아보도록 하겠습니다.
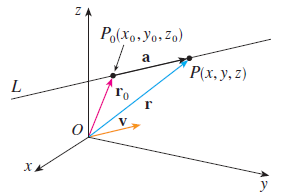
먼저, 직선을 설명하기 위해서 위와 같은 그림을 고려해보겠습니다. 직선 $L$을 정의하기 위해서는 어떤 정보가 필요할까요? 일단, 어떤 점을 지나는 지가 필요할 것입니다. 위 그림에서는 이를 $P_{0}(x_{0}, y_{0}, z_{0})$라고 두었습니다. 문제는 3차원에서 점 하나를 지나는 직선은 무한히 많습니다. 따라서, 이를 하나의 직선으로 결정해주기 위한 정보가 한 가지 더 필요합니다. 바로 방향(direction)이죠. 위 그림에서는 이를 $\mathbf{a}$라는 벡터로 표현하였습니다. 즉, 점 $P_{0}(x_{0}, y_{0}, z_{0})$를 지나는 $\mathbf{a}$ 방향의 직선은 단 하나밖에 존재하지 않습니다.
기본적인 개념 설명은 여기까지입니다. 이제 실제로 3차원에서 대수적으로 직선을 표현하는 방법을 생각해보도록 하죠. 결국에는 $\mathbf{a}$를 생각하기 위해서는 직선 $L$의 임의의 점 $P(x, y, z)$를 고려해야합니다. 그리고, $\mathbf{r}_{0} = \vec{OP_{0}}, \mathbf{r} = \vec{OP}$라고 두겠습니다. 그러면, 미적분학 - 벡터에서 보았던 삼각법을 통해서 $\mathbf{r} = \mathbf{r}_{0} + \mathbf{a}$라는 식을 얻을 수 있습니다. 마지막으로 벡터 $\mathbf{a}$와 동일한 방향이지만, 원점을 시작점으로 가지는 벡터 $\mathbf{v}$를 생각해보겠습니다. 이때, $\mathbf{a}$와 $\mathbf{v}$는 서로 평행한 벡터이기 때문에 $\mathbf{a} = t\mathbf{v}$를 만족하는 어떤 스칼라 $t \in \mathbb{R}$이 존재합니다.
$$\mathbf{r} = \mathbf{r}_{0} + \mathbf{a} = \mathbf{r}_{0} + t\mathbf{v}$$
저희는 위 방정식을 직선 $L$의 벡터 방정식(vector equation)이라고 하겠습니다. 이제 $\mathbf{v} = <a, b, c>, \mathbf{r} = <x, y, z>$, 그리고 $\mathbf{r}_{0} = <x_{0}, y_{0}, z_{0}>$라고 두겠습니다. 그러면 위 방정식을 다시 쓸 수 있습니다.
$$<x, y, z> = <x_{0}, y_{0}, z_{0}> + t<a, b, c> = <x_{0} + ta, y_{0} + tb, z_{0} + tc>$$
이때, $t \in \mathbb{R}$이며 위 방정식을 매개변수 방정식(parametric equation)이라고 부릅니다.
예제1. 점 $P(5, 1, 3)$을 지나고 벡터 $\mathbf{v} = <1, 4, -2>$와 평행한 직선의 방정식을 매개변수 방정식으로 구하여라.
이때, $\mathbf{r}_{0} = <5, 1, 3>$이고 직선의 방향이 $\mathbf{v} = <1, 4, -2>$이기 때문에 매개변수 방정식으로 직선을 표현하면 아래와 같다.
$$\begin{cases} x &= 5 + t \\ y &= 1 + 4t \\ z &= 3 -2t \end{cases}$$
위와 같이 매개변수 방정식으로 직선을 표현할 수 있지만, 대칭 방정식(symmetric equation)이라는 형태로도 표현할 수 있습니다. 매개변수 방정식에서 유심히 볼 것은 $x, y, z$ 모두 매개변수 $t$에 묶여있다는 점입니다. 따라서, 이를 더 깔끔하게 표현할 수 있을텐데요. 아래와 같이 쓸 수 있습니다.
$$\frac{x - x_{0}}{a} = \frac{y - y_{0}}{b} = \frac{z - z_{0}}{c} = t$$
예제2. 점 $P(5, 1, 3)$을 지나고 벡터 $\mathbf{v} = <1, 4, -2>$와 평행한 직선의 방정식을 대칭 방정식으로 구하여라.
이때, $\mathbf{r}_{0} = <5, 1, 3>$이고 직선의 방향이 $\mathbf{v} = <1, 4, -2>$이기 때문에 대칭 방정식으로 직선을 표현하면 아래와 같다.
$$\frac{x - 5}{1} = \frac{y - 1}{4} = \frac{z - 3}{-2} = t$$

이번에는 3차원에서 평면을 생각해보겠습니다. 직선과 마찬가지로 위 그림을 고려해보겠습니다. 일단, 평면을 정의하기 위해서는 어떤 정보가 필요할 지 생각해보겠습니다. 가장 먼저 필요한 것은 어떤 점을 지나는 지 입니다. 위 그림에서는 이를 $P_{0}(x_{0}, y_{0}, z_{0})$로 표현하였습니다. 다음으로 필요한 정보는 "평면의 방향"입니다. 이때, 유의할 점은 직선과 동일하게 평행한 방향의 벡터를 고려하는 것이 아니라 평면과 수직인 방향의 벡터 $\mathbf{n}$을 고려해야합니다. 그러면 3차원에서 유일한 평면이 정의가 되죠. 즉, 점 $P_{0}(x_{0}, y_{0}, z_{0})$를 지나고 벡터 $\mathbf{n}$에 수직인 평면은 단 하나밖에 존재하지 않습니다.
기본적인 개념 설명은 여기까지입니다. 이제 실제로 3차원에서 대수적으로 평면을 표현하는 방법을 생각해보도록 하죠. 여기서 중요한 것은 평면과 벡터 $\mathbf{n}$이 서로 수직(perpendicular)라는 것입니다. 따라서, 평면 위의 임의의 점 $P(x, y, z)$를 잡으면 벡터 $\vec{P_{0}P}$를 고려했을 때, $\vec{P_{0}P} \perp \mathbf{n}$임을 알 수 있습니다. 여기서 미적분학 - 벡터의 내적에서 수직 관계의 두 벡터를 서로 내적하면 0이 나온다는 정리를 이용합니다.
$$\mathbf{n} \cdot \vec{P_{0}P} = \mathbf{n} \cdot (\mathbf{r} - \mathbf{r}_{0}) = 0 \Rightarrow \mathbf{n} \cdot \mathbf{r} = \mathbf{n} \cdot \mathbf{r}_{0}$$
저희는 위 방정식을 평면의 벡터 방정식(vector equation)이라고 하겠습니다. 이제 $\mathbf{v} = <a, b, c>, \mathbf{r} = <x, y, z>$, 그리고 $\mathbf{r}_{0} = <x_{0}, y_{0}, z_{0}>$라고 두겠습니다. 그러면 위 방정식을 다시 쓸 수 있습니다.
$$<a, b, c> \cdot <x - x_{0}, y - y_{0}, z - z_{0}> = 0 \Rightarrow a(x - x_{0}) + b(y - y_{0}) + c(z - z_{0}) = 0$$
이를 평면의 스칼라 방정식(scalar equation)이라고 부릅니다. 이때, 평면에 수직인 벡터 $\mathbf{n}$을 법선벡터(normal vector)라고 부릅니다.
예제3. 점 $P(2, 4, -1)$을 지나고 법선벡터 $\mathbf{n} = <2, 3, 4>$를 가지는 평면을 스칼라 방정식으로 표현하라.
이때, $P(2, 4, -1)$을 지나고 법선벡터가 $\mathbf{n} = <2, 3, 4>$이기 때문에 스칼라 방정식으로 평면을 표현하면 아래와 같다.
$$2(x - 2) + 3(y - 4) + 4(z + 1) = 0 \Rightarrow 2x + 3y + 4z = 12$$
그렇다면 법선벡터 $\mathbf{n}$이 주어지지 않고 세 점을 포함하는 평면을 구하는 경우에는 어떻게 해야할까요? 즉, 세 개의 점 $P(1, 3, 2), Q(3, -1, 6), R(5, 2, 0)$이 주어졌다고 가정했을 때, 평면을 구해보겠습니다. 먼저 평면이 어떤 점을 지나는 지는 알고 있기 때문에 점 $P$를 기준으로 하고 법선벡터 $\mathbf{n}$을 찾아야 합니다. 일단, 첫번째로 할 것은 3개의 점을 이용해서 2개의 벡터를 만들어주는 것입니다.
$$\mathbf{a} = \vec{PQ} = \vec{OQ} - \vec{OP} = <3, -1, 6> - <1, 3, 2> = <2, -4, 4>$$
$$\mathbf{b} = \vec{PR} = \vec{OR} - \vec{OP} = <5, 2, 0> - <1, 3, 2> = <4, -1, -2>$$
그러면 미적분학 - 벡터의 외적에서 정리2에 의해서 $\mathbf{a}, \mathbf{b}$의 외적을 법선벡터로 삼으면 됩니다. 따라서 아래와 같이 구할 수 있죠.
$$\mathbf{n} = \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & -4 & 4 \\ 4 & -1 & -2 \end{vmatrix} = <12, 20, 14>$$
따라서, 위 세 점을 지나는 평면의 방정식은 아래와 같습니다.
$$12(x - 1) + 20(y - 3) + 14(z - 2) = 0 \Rightarrow 6x + 10y + 7z = 50$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 3차원 원통과 이차곡면 (0) | 2022.05.27 |
|---|---|
| 미적분학 - 3차원 두 평면이 교차하는 직선 (0) | 2022.05.26 |
| 미적분학 - 벡터의 외적 (1) | 2022.05.24 |
| 미적분학 - 벡터의 방향각과 사영 (0) | 2022.05.22 |
| 미적분학 - 벡터의 내적 (0) | 2022.05.21 |
