안녕하세요. 지난 포스팅의 미적분학 - 벡터의 성분에서는 벡터를 좌표평면 상에 표현하는 방법과 그에 따른 성질에 대해서 알아보았습니다. 오늘은 벡터하면 빼놓을 수 없는 중요한 연산인 내적(inner product)에 대해서 알아보도록 하겠습니다.
정의1. 내적(inner product, dot product, scalar product)
두 벡터 $\mathbf{a} = <a_{1}, a_{2}, a_{3}>$와 $\mathbf{b} = <b_{1}, b_{2}, b_{3}>$가 주어졌다고 하자. 이때, 두 벡터 $\mathbf{a}, \mathbf{b}$ 사이의 내적은 아래와 같이 정의된다.
$$\mathbf{a} \cdot \mathbf{b} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$$
만약, 두 벡터가 2차원 상의 벡터라면 아래와 같다.
$$\mathbf{a} \cdot \mathbf{b} = a_{1}b_{1} + a_{2}b_{2}$$
정리1. 내적의 성질
세 벡터 $\mathbf{a}, \mathbf{b}, \mathbf{c}$와 임의의 스칼라 $c$가 있다고 하자.
1. $\mathbf{a} \cdot \mathbf{a} = \left|\mathbf{a}\right|^{2}$
2. 교환법칙(commutative law) : $\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$
3. 분배법칙(distributive law) : $\mathbf{a} \cdot \left(\mathbf{b} + \mathbf{c}\right) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}$
4. $\left(c\mathbf{a}\right) \cdot \mathbf{b} = c(\mathbf{a} \cdot \mathbf{b}) = a \cdot (c\mathbf{b})$
5. $\mathbf{0} \cdot \mathbf{a} = \mathbf{0}$
정리2. 두 벡터 사이의 내적 계산법
두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 있고 두 벡터가 이루는 각도를 $\theta$라고 하자. 그러면 두 벡터의 내적을 아래와 같이 구할 수 있다.
$$\mathbf{a} \cdot \mathbf{b} = \left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta)$$
증명
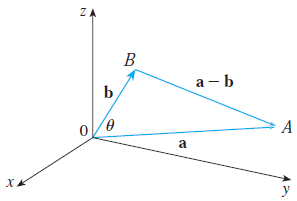
위와 같은 그림을 고려한다. 이때, 코사인 삼각법에 의해서 아래와 같은 등식을 얻을 수 있다.
$$\left|AB\right|^{2} = \left|OA\right|^{2} + \left|OB\right|^{2} - 2\left|OA\right|\left|OB\right|\cos(\theta)$$
여기서, $\left|OA\right| = \left|\mathbf{a}\right|, \left|OB\right| = \left|\mathbf{b}\right|, \left|AB\right| = \left|\mathbf{a} - \mathbf{b}\right|$임을 상기한다. 따라서, 위의 등식을 아래와 같이 쓸 수 있다.
$$\left|\mathbf{a} - \mathbf{b}\right|^{2} = \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta)$$
이때, 정리1의 법칙들을 사용하여 좌항을 아래와 같이 정리가능하다.
$$\begin{align*} \left|\mathbf{a} - \mathbf{b}\right|^{2} &= \left(\mathbf{a} - \mathbf{b}\right) \cdot \left(\mathbf{a} - \mathbf{b}\right) \\ &= \mathbf{a} \cdot \mathbf{a} - 2 \mathbf{a} \cdot \mathbf{b} + \mathbf{b} \cdot \mathbf{b} \\ &= \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\mathbf{a} \cdot \mathbf{b} \end{align*}$$
따라서, 기존의 식을 다시 정리할 수 있다.
$$\begin{align*} &\left|\mathbf{a} - \mathbf{b}\right|^{2} = \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta) \\ \Rightarrow& \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\mathbf{a} \cdot \mathbf{b} = \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta) \\ \Rightarrow& \mathbf{a} \cdot \mathbf{b} = \left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta)\end{align*}$$
따름정리2-1. 두 벡터 사이의 각도
두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 있고 두 벡터가 이루는 각도를 $\theta$라고 하자.
$$\cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{\left|\mathbf{a}\right| \left|\mathbf{b}\right|}$$
정의2. 직교성(Orthogonality)
두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 $\theta = 0$이라면 두 벡터는 서로 직교(Orthogonal)한다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 벡터의 외적 (0) | 2022.05.24 |
|---|---|
| 미적분학 - 벡터의 방향각과 사영 (0) | 2022.05.22 |
| 미적분학 - 벡터의 성분 (0) | 2022.05.20 |
| 미적분학 - 벡터 (0) | 2022.05.18 |
| 미적분학 - 3차원 좌표계 (0) | 2022.05.17 |
안녕하세요. 지난 포스팅의 미적분학 - 벡터의 성분에서는 벡터를 좌표평면 상에 표현하는 방법과 그에 따른 성질에 대해서 알아보았습니다. 오늘은 벡터하면 빼놓을 수 없는 중요한 연산인 내적(inner product)에 대해서 알아보도록 하겠습니다.
정의1. 내적(inner product, dot product, scalar product)
두 벡터 $\mathbf{a} = <a_{1}, a_{2}, a_{3}>$와 $\mathbf{b} = <b_{1}, b_{2}, b_{3}>$가 주어졌다고 하자. 이때, 두 벡터 $\mathbf{a}, \mathbf{b}$ 사이의 내적은 아래와 같이 정의된다.
$$\mathbf{a} \cdot \mathbf{b} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$$
만약, 두 벡터가 2차원 상의 벡터라면 아래와 같다.
$$\mathbf{a} \cdot \mathbf{b} = a_{1}b_{1} + a_{2}b_{2}$$
정리1. 내적의 성질
세 벡터 $\mathbf{a}, \mathbf{b}, \mathbf{c}$와 임의의 스칼라 $c$가 있다고 하자.
1. $\mathbf{a} \cdot \mathbf{a} = \left|\mathbf{a}\right|^{2}$
2. 교환법칙(commutative law) : $\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$
3. 분배법칙(distributive law) : $\mathbf{a} \cdot \left(\mathbf{b} + \mathbf{c}\right) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}$
4. $\left(c\mathbf{a}\right) \cdot \mathbf{b} = c(\mathbf{a} \cdot \mathbf{b}) = a \cdot (c\mathbf{b})$
5. $\mathbf{0} \cdot \mathbf{a} = \mathbf{0}$
정리2. 두 벡터 사이의 내적 계산법
두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 있고 두 벡터가 이루는 각도를 $\theta$라고 하자. 그러면 두 벡터의 내적을 아래와 같이 구할 수 있다.
$$\mathbf{a} \cdot \mathbf{b} = \left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta)$$
증명

위와 같은 그림을 고려한다. 이때, 코사인 삼각법에 의해서 아래와 같은 등식을 얻을 수 있다.
$$\left|AB\right|^{2} = \left|OA\right|^{2} + \left|OB\right|^{2} - 2\left|OA\right|\left|OB\right|\cos(\theta)$$
여기서, $\left|OA\right| = \left|\mathbf{a}\right|, \left|OB\right| = \left|\mathbf{b}\right|, \left|AB\right| = \left|\mathbf{a} - \mathbf{b}\right|$임을 상기한다. 따라서, 위의 등식을 아래와 같이 쓸 수 있다.
$$\left|\mathbf{a} - \mathbf{b}\right|^{2} = \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta)$$
이때, 정리1의 법칙들을 사용하여 좌항을 아래와 같이 정리가능하다.
$$\begin{align*} \left|\mathbf{a} - \mathbf{b}\right|^{2} &= \left(\mathbf{a} - \mathbf{b}\right) \cdot \left(\mathbf{a} - \mathbf{b}\right) \\ &= \mathbf{a} \cdot \mathbf{a} - 2 \mathbf{a} \cdot \mathbf{b} + \mathbf{b} \cdot \mathbf{b} \\ &= \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\mathbf{a} \cdot \mathbf{b} \end{align*}$$
따라서, 기존의 식을 다시 정리할 수 있다.
$$\begin{align*} &\left|\mathbf{a} - \mathbf{b}\right|^{2} = \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta) \\ \Rightarrow& \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\mathbf{a} \cdot \mathbf{b} = \left|\mathbf{a}\right|^{2} + \left|\mathbf{b}\right|^{2} - 2\left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta) \\ \Rightarrow& \mathbf{a} \cdot \mathbf{b} = \left|\mathbf{a}\right|\left|\mathbf{b}\right|\cos(\theta)\end{align*}$$
따름정리2-1. 두 벡터 사이의 각도
두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 있고 두 벡터가 이루는 각도를 $\theta$라고 하자.
$$\cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{\left|\mathbf{a}\right| \left|\mathbf{b}\right|}$$
정의2. 직교성(Orthogonality)
두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 $\theta = 0$이라면 두 벡터는 서로 직교(Orthogonal)한다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 벡터의 외적 (0) | 2022.05.24 |
|---|---|
| 미적분학 - 벡터의 방향각과 사영 (0) | 2022.05.22 |
| 미적분학 - 벡터의 성분 (0) | 2022.05.20 |
| 미적분학 - 벡터 (0) | 2022.05.18 |
| 미적분학 - 3차원 좌표계 (0) | 2022.05.17 |
