안녕하세요. 지난 포스팅의 미적분학 - 3차원 좌표계에서는 3차원 좌표계를 이루는 구성요소들(원점, 축, 평면)과 3차원의 두 점 사이의 거리를 구하는 공식과 구를 대수적으로 표현하는 방법에 대해서 알아보았습니다. 오늘은 이어서 벡터(vector)에 대한 이야기를 해보도록 하겠습니다.

간단히 말해서 벡터란 크기(magnitude)와 방향성(direction)을 동시에 표현할 수 있는 단위입니다. 따라서, 벡터에서는 방향성이 중요한 요소이기 때문에 이를 표현하기 위해 위와 같이 화살표 기호로 표기합니다. 그리고 일반적으로 방향성이 존재하지 않고 크기만 존재하는 경우에는 스칼라(scalar)라고 하며 $u$나 $v$로 표기합니다. 만약, 방향성이 포함된 벡터라면 $\mathbf{u}$나 $\mathbf{v}$와 같이 bold체로 표기하게 되죠. 또는 $\vec{u}$나 $\vec{v}$와 같이 화살표를 문자 위에 적어서 표기할 수도 있죠.
이제 위의 그림을 보도록 하죠. 벡터는 방향성이 존재하기 때문에 시작점(initial point)과 끝점(terminal point)가 존재합니다. 예를 들어, $\mathbf{u}$와 $\mathbf{v}$의 시작점은 각각 점 $A$와 $C$이고 끝점은 점 $B$와 $D$입니다. 이와 같이 시작점과 끝점을 명시해주기 위해서 $\vec{AB}$나 $\vec{CD}$와 같이 표기하기도 합니다.
그렇다면 두 벡터가 "같다"라는 것은 어떤 것을 의미할까요? 스칼라에서는 크기만 고려하면 되기 때문에 오직 두 스칼라의 크기만 같으면 그냥 같습니다. 하지만 벡터에서는 방향성까지 고려하기 때문에 크기가 같더라도 방향이 다르면 다른 벡터입니다. 따라서, 두 벡터가 같다는 것은 크기와 방향이 모두 동일하다는 것을 의미합니다. 만약, 두 벡터가 같다면 $\mathbf{u} = \mathbf{v}$라고 쓸 수 있습니다.
마지막으로 크기가 존재하지 않는 벡터도 있습니다. 이를 영벡터(zero vector)라고 하고 $\mathbf{0}$ 또는 $\vec{0}$이라고 씁니다. 이 경우에는 크기가 없기 때문에 방향성도 하나로 정해질 수 없습니다.
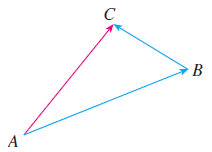
다음으로 두 벡터의 연산에 대해서 알아보겠습니다. 두 벡터의 연산은 기하학적으로 위와 같이 정의됩니다. 두 벡터 $\vec{AB}$와 $\vec{BC}$를 더하는 경우를 고려해보겠습니다. 보시면 최종적으로 벡터 $\vec{AC}$를 얻을 수 있는 것을 볼 수 있습니다.
$$\vec{AB} + \vec{BC} = \vec{AC}$$
위와 같이 계산하는 방법을 삼각법(Triangular Law)라고 합니다.

그렇다면 벡터에 스칼라 곱을 하면 어떻게 될까요? 위의 그림과 마찬가지로 양수인 스칼라를 곱하면 방향은 변하지 않고 그 스칼라만큼 배가 되어 크기가 늘어나게 됩니다. 그와 반면에 음수인 스칼라를 곱하면 방향은 기존 벡터의 180도 반대 방향이 되고 크기 역시 늘어나게 됩니다. 이를 통해서 두 벡터 사이의 뺄셈도 정의할 수 있게 됩니다.
$$\mathbf{u} - \mathbf{v} = \mathbf{u} + \left(-\mathbf{v}\right)$$
즉, 두 벡터 사이의 뺄셈은 벡터의 방향을 반대로 회전시킨 다음 더하는 것과 마찬가지입니다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 벡터의 내적 (0) | 2022.05.21 |
|---|---|
| 미적분학 - 벡터의 성분 (0) | 2022.05.20 |
| 미적분학 - 3차원 좌표계 (0) | 2022.05.17 |
| 미적분학 - 복잡한 함수의 테일러 급수 (0) | 2022.05.16 |
| 미적분학 - 테일러 급수와 맥클로린 급수 (0) | 2022.05.15 |
