안녕하세요. 지난 포스팅의 미적분학 - 벡터에서는 벡터의 정의와 벡터합과 차를 계산하는 방법에 대해서 알아보았습니다. 오늘은 벡터를 표현하는 방법에 대해서 알아보도록 하겠습니다.
지난 포스팅에서 벡터를 정의하기 위해서는 시작점과 끝점이 필요하다고 말씀드렸습니다. 따라서 이 두 가지만 정해준다면 크기와 방향성을 지정할 수 있습니다. 하지만 대부분은 시작점을 원점 $O$로 고정하게 됩니다. 끝점만 $(a_{1}, a_{2})$와 같이 좌표의 형태로 지정해줍니다. 이 말은 원점 $O$에서 시작해서 $(a_{1}, a_{2})$에서 끝나는 벡터를 의미하죠. 이를 표현하면 아래와 같습니다.
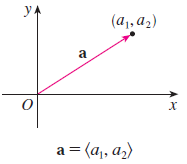
$$\mathbf{u} = <a_{1}, a_{2}>$$
이를 3차원으로 표현할 수도 있습니다.
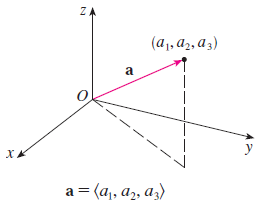
$$\mathbf{u} = <a_{1}, a_{2}, a_{3}>$$
벡터의 표현방법을 익히셨다면 다음부터는 쉽습니다. 벡터의 합과 차 역시 쉽게 정의가 되거든요. 두 벡터 $\mathbf{u} = <a_{1}, a_{2}>$와 $\mathbf{v} = <b_{1}, b_{2}>$가 있다고 가정하겠습니다.
- 두 벡터의 합 : $\mathbf{u} + \mathbf{v} = <a_{1}, a_{2}> + <b_{1}, b_{2}> = <a_{1} + b_{1}, a_{2} + b_{2}>$
- 두 벡터의 차 : $\mathbf{u} - \mathbf{v} = <a_{1}, a_{2}> - <b_{1}, b_{2}> = <a_{1} - b_{1}, a_{2} - b_{2}>$
- 스칼라곱 : $c\mathbf{u} = c<a_{1}, a_{2}> = <ca_{1}, ca_{2}>$
이때, $c$는 임의의 실수입니다. 간단한 예제로 두 점 $A(x_{1}, y_{1}, z_{1})$과 $B(x_{2}, y_{2}, z_{2})$가 주어졌을 때, 벡터 $\vec{AB}$를 어떻게 구할 수 있을까요? 방법은 간단합니다. 일단, 원점 $O$를 중심으로 점 $A$로의 벡터 $\vec{OA}$와 점 $B$로의 벡터 $\vec{OB}$를 각각 생각해보겠습니다. 그러면 두 벡터의 차 공식에 의해서 아래와 같이 $\vec{AB}$를 얻을 수 있습니다.
$$\vec{AB} = \vec{OB} - \vec{OA} = <x_{1} - x_{2}, y_{1} - y_{2}, z_{1} - z_{2}>$$
그렇다면 벡터의 크기는 어떻게 구할까요?
- 2차원 벡터 $\mathbf{u} = <a_{1}, a_{2}>$ : $\left|\mathbf{a}\right| = \sqrt{a_{1}^{2} + a_{2}^{2}}$
- 3차원 벡터 $\mathbf{u} = <a_{1}, a_{2}, a_{3}>$ : $\left|\mathbf{a}\right| = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}}$

또한 이 벡터에는 위의 8가지 중요한 성질들이 존재합니다. 각 성질들은 보시면 직관적으로 이해하실 수 있기 때문에 참고만 하시면 됩니다. 마지막으로 단위벡터(unit vector)라는 것이 있습니다. 단위벡터란 차원을 이루는 표준기저벡터(standard basis vector)로 자세한 내용은 선형대수학 - 기저와 차원을 참고해주시면 됩니다.
- 2차원 단위벡터 : $\mathbf{i} = <1, 0>, \mathbf{j} = <0, 1>$
- 3차원 단위벡터 : $\mathbf{i} = <1, 0, 0>, \mathbf{j} = <0, 1, 0>, \mathbf{k} = <0, 0, 1>$
따라서 임의의 벡터를 단위벡터를 이용해서 쓸 수도 있습니다.
$$\begin{align*} \mathbf{a} &= <a_{1}, a_{2}, a_{3}> \\ &= <a_{1}, 0, 0> + <0, a_{2}, 0> + <0, 0, a_{3}> \\ &= a_{1} \mathbf{i} + a_{2} j=\mathbf{j} + a_{3} \mathbf{k} \end{align*}$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 벡터의 방향각과 사영 (0) | 2022.05.22 |
|---|---|
| 미적분학 - 벡터의 내적 (0) | 2022.05.21 |
| 미적분학 - 벡터 (0) | 2022.05.18 |
| 미적분학 - 3차원 좌표계 (0) | 2022.05.17 |
| 미적분학 - 복잡한 함수의 테일러 급수 (0) | 2022.05.16 |
안녕하세요. 지난 포스팅의 미적분학 - 벡터에서는 벡터의 정의와 벡터합과 차를 계산하는 방법에 대해서 알아보았습니다. 오늘은 벡터를 표현하는 방법에 대해서 알아보도록 하겠습니다.
지난 포스팅에서 벡터를 정의하기 위해서는 시작점과 끝점이 필요하다고 말씀드렸습니다. 따라서 이 두 가지만 정해준다면 크기와 방향성을 지정할 수 있습니다. 하지만 대부분은 시작점을 원점 O로 고정하게 됩니다. 끝점만 (a1,a2)와 같이 좌표의 형태로 지정해줍니다. 이 말은 원점 O에서 시작해서 (a1,a2)에서 끝나는 벡터를 의미하죠. 이를 표현하면 아래와 같습니다.

u=<a1,a2>
이를 3차원으로 표현할 수도 있습니다.

u=<a1,a2,a3>
벡터의 표현방법을 익히셨다면 다음부터는 쉽습니다. 벡터의 합과 차 역시 쉽게 정의가 되거든요. 두 벡터 u=<a1,a2>와 v=<b1,b2>가 있다고 가정하겠습니다.
- 두 벡터의 합 : u+v=<a1,a2>+<b1,b2>=<a1+b1,a2+b2>
- 두 벡터의 차 : u−v=<a1,a2>−<b1,b2>=<a1−b1,a2−b2>
- 스칼라곱 : cu=c<a1,a2>=<ca1,ca2>
이때, c는 임의의 실수입니다. 간단한 예제로 두 점 A(x1,y1,z1)과 B(x2,y2,z2)가 주어졌을 때, 벡터 →AB를 어떻게 구할 수 있을까요? 방법은 간단합니다. 일단, 원점 O를 중심으로 점 A로의 벡터 →OA와 점 B로의 벡터 →OB를 각각 생각해보겠습니다. 그러면 두 벡터의 차 공식에 의해서 아래와 같이 →AB를 얻을 수 있습니다.
→AB=→OB−→OA=<x1−x2,y1−y2,z1−z2>
그렇다면 벡터의 크기는 어떻게 구할까요?
- 2차원 벡터 u=<a1,a2> : |a|=√a21+a22
- 3차원 벡터 u=<a1,a2,a3> : |a|=√a21+a22+a23

또한 이 벡터에는 위의 8가지 중요한 성질들이 존재합니다. 각 성질들은 보시면 직관적으로 이해하실 수 있기 때문에 참고만 하시면 됩니다. 마지막으로 단위벡터(unit vector)라는 것이 있습니다. 단위벡터란 차원을 이루는 표준기저벡터(standard basis vector)로 자세한 내용은 선형대수학 - 기저와 차원을 참고해주시면 됩니다.
- 2차원 단위벡터 : i=<1,0>,j=<0,1>
- 3차원 단위벡터 : i=<1,0,0>,j=<0,1,0>,k=<0,0,1>
따라서 임의의 벡터를 단위벡터를 이용해서 쓸 수도 있습니다.
a=<a1,a2,a3>=<a1,0,0>+<0,a2,0>+<0,0,a3>=a1i+a2j=j+a3k
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 벡터의 방향각과 사영 (0) | 2022.05.22 |
|---|---|
| 미적분학 - 벡터의 내적 (0) | 2022.05.21 |
| 미적분학 - 벡터 (0) | 2022.05.18 |
| 미적분학 - 3차원 좌표계 (0) | 2022.05.17 |
| 미적분학 - 복잡한 함수의 테일러 급수 (0) | 2022.05.16 |
