안녕하세요. 지난 포스팅의 미적분학 - 복잡한 함수의 테일러 급수에서는 $\sin(x), \cos(x)$를 맥클로린 급수로 표현하는 방법과 이항급수(bionomial series)에 대해서 알아보았습니다. 오늘은 새로운 주제로 넘어가서 3차원에 대한 이야기를 해보도록 하겠습니다. 이를 위해서 3차원 좌표계를 어떤 식으로 정의하는 지부터 알아보도록 하죠.
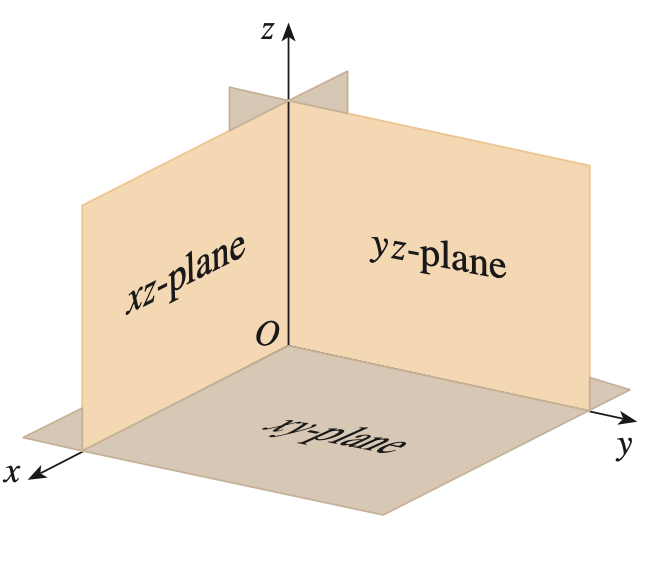
기본적으로 3차원 좌표계는 위와 같이 이루어져 있습니다. 일단, 원점(origin point) $O$가 있습니다. 2차원 좌표계에서와 마찬가지로 기준점의 역할을 하게 됩니다. 그리고 원점을 기준으로 뻗어나가는 3개의 좌표 축(coordinate axis) $x, y, z$를 볼 수 있습니다. 이 역시 2차원 좌표계와 마찬가지입니다. 다만, 다른 점은 지금까지 2차원 좌표계에서는 $x$와 $y$로만 정의하여 높이에 대한 정의를 할 수 없었습니다. 하지만, 3차원 좌표계에서는 $z$축을 도입함으로써 높이를 표현할 수 있고 이는 곧 입체를 대수적으로 표현할 수 있음을 의미합니다. 그리고 2개의 좌표계로 구성되는 평면(plane)이 존재합니다. 각각 $xy$-평면, $yz$-평면, $zx$-평면입니다.
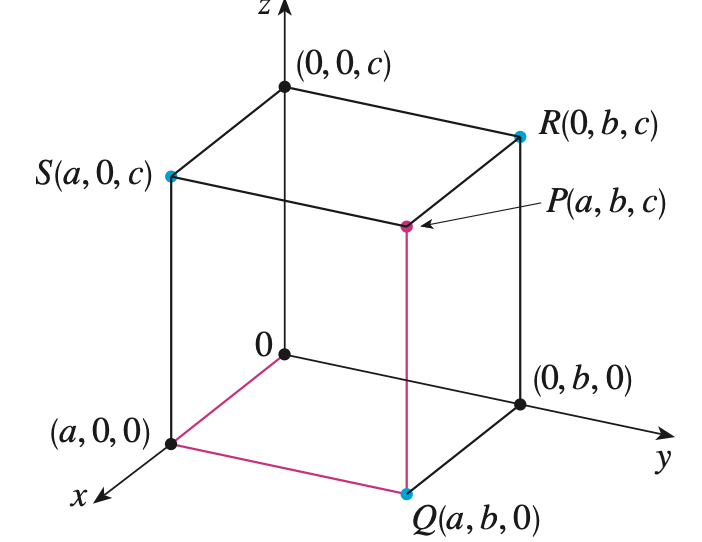
다음으로 3차원 좌표계에서 점의 위치를 표현하는 방법입니다. 생각보다 간단합니다. 임의의 점 $P(a, b, c)$가 주어졌다고 하겠습니다. 그러면 이 점의 좌표는 $x$-축 방향으로 $a$만큼, $y$-축 방향으로 $b$만큼, $z$-축 방향으로 $c$만큼 이동했다고 볼 수 있습니다. 이와 같이 3개의 실수로 점의 위치를 표현하는 3차원 좌표계를 "3차원 직교좌표계(three-dimensional rectangular coordinate system)"이라고 합니다. 그리고 이를 수학적으로 표현하면 아래와 같죠.
$$\mathbb{R} \times \mathbb{R} \times \mathbb{R} = \{(x, y, z) | x, y, z \in \mathbb{R}\}$$
여기서 $\times$는 데카르트 곱 또는 카르테시안 곱(cartesian product)라고 불리는 집합 연산으로 두 개 이상의 집합이 주어졌을 때 각 집합의 임의의 원소들로 순서쌍을 만들게 됩니다.

3차원 좌표계에서 점의 위치를 어떻게 정의하는 지까지 알아보았으므로 이번에는 3차원에서 간단한 대수방정식이 어떤식으로 그려지는 지 보도록 하겠습니다. 왼쪽 그림은 $z = 3$의 그래프를 3차원으로 보여주고 있습니다. 잘 보시면 $x$와 $y$의 값에 관계없이 $z = 3$인 조건만 만족하며 쭉 뻗어있는 것을 볼 수 있습니다. 오른쪽 그림도 마찬가지로 $y = 5$라는 제한만 존재하기 때문에 $x$와 $z$의 값에 관계없이 평면이 생성되는 것을 볼 수 있습니다.
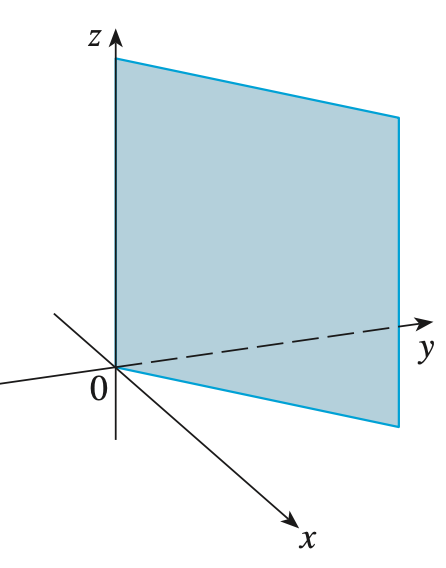
위의 그림은 $y = x$를 3차원으로 그린것입니다. 주어진 제한은 오직 $x = y$이기 때문에 $z$의 값에 관계없이 평면이 형성되는 것을 볼 수 있습니다.
정리1. 3차원에서 두 점 사이의 거리(Distance formula in three-dimension)
3차원 좌표계에서 임의의 두 점 $P_{1}(x_{1}, y_{1}, z_{1})$과 $P_{2}(x_{2}, y_{2}, z_{2})$가 주어졌다고 가정하자. 그러면 두 점 사이의 거리 $\bar{P_{1}P_{2}}$는 아래와 같이 정의된다.
$$\bar{P_{1}P_{2}} = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2} + (z_{1} - z_{2})^{2}}$$
예제1. 두 점 $P(2, -1, 7)$과 $Q(1, -3, 5)$ 사이의 거리를 구하여라.
$$\begin{align*} \bar{PQ} &= \sqrt{(2 - 1)^{2} + (-1 + 3)^{2} + (7 - 5)^{2}} \\ &= \sqrt{1 + 4 + 4} \\ &= \sqrt{9} = 3 \end{align*}$$
정의1. 3차원에서 구의 방정식(Equation of Sphere in three-dimension)
구의 중심 $C(a, b, c)$와 반지름 $r$이 주어졌을 때 3차원에서 구의 방정식은 아래와 같이 쓸 수 있다.
$$(x - a)^{2} + (y - b)^{2} + (z - c)^{2} = r^{2}$$
이때, 중심이 원점 $O$이고 반지름이 $1$인 구를 단위 구(unit sphere)라고 한다.
$$x^{2} + y^{2} + z^{2} = 1$$
예제2. $x^{2} + y^{2} + z^{2} + 4x - 6y + 2z + 6 = 0$이 3차원에서 구임을 보이고 구의 중심과 반지름을 구하여라.
$$\begin{align*} &x^{2} + y^{2} + z^{2} + 4x - 6y + 2z + 6 = 0 \\ \Rightarrow& (x^{2} + 4x + 4) + (y^{2} - 6y + 9) + (z^{2} + 2z + 1) = -6 + 4 + 9 + 1 \\ \Rightarrow& (x + 2)^{2} + (y - 3)^{2} + (z + 1)^{2} = 8 \end{align*}$$
따라서, 구의 중심은 $C(-2, 3, -1)$이고 반지름은 $r = \sqrt{8}$이다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 벡터의 성분 (0) | 2022.05.20 |
|---|---|
| 미적분학 - 벡터 (0) | 2022.05.18 |
| 미적분학 - 복잡한 함수의 테일러 급수 (0) | 2022.05.16 |
| 미적분학 - 테일러 급수와 맥클로린 급수 (0) | 2022.05.15 |
| 미적분학 - 함수의 멱급수 표현 (0) | 2022.05.14 |
