안녕하세요. 지난 포스팅의 미적분학 - 벡터의 내적에서는 내적의 정의와 그와 관련된 성질 몇 가지에 대해서 알아보았습니다. 특히, 중요한 것은 벡터의 내적을 통해서 두 벡터가 이루는 각도를 구할 수 있다는 점입니다. 이 부분은 오늘 알아볼 벡터의 방향각(direction angle)을 구하는 데 중요하기 때문에 꼭 알아두셔야 합니다. 또한 벡터를 다른 벡터에 사영(projection) 시킨다는 것이 어떤 의미인지 알아보도록 하겠습니다.
정의1. 방향각(direction angle)
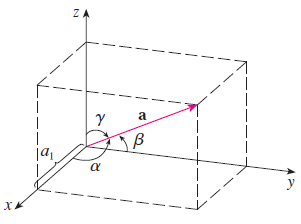
벡터 $\mathbf{a} = <a_{1}, a_{2}, a_{3}>$의 방향각은 $x, y, z$-축과 이루는 각도 $\alpha, \beta, \gamma$로 정의된다.
$$\cos(\alpha) = \frac{a_{1}}{\left|\mathbf{a}\right|}, \cos(\beta) = \frac{a_{2}}{\left|\mathbf{a}\right|}, \cos(\gamma) = \frac{a_{3}}{\left|\mathbf{a}\right|}$$
설명
방향각을 이용해서 임의의 벡터 $\mathbf{a}$를 다르게 쓸 수 있습니다.
$$a_{1} = |\mathbf{a}|\cos(\alpha), a_{2} = |\mathbf{a}|\cos(\beta), a_{3} = |\mathbf{a}|\cos(\gamma)$$
방향각의 정의에 따라서 저희는 벡터의 각 성분을 위와 같이 벡터의 방향각으로 쓸 수 있습니다.
$$\begin{align*} \mathbf{a} &= <a_{1}, a_{2}, a_{3}> \\ &= <|\mathbf{a}|\cos(\alpha), |\mathbf{a}|\cos(\beta), |\mathbf{a}|\cos(\gamma)> \\ &= |\mathbf{a}|<\cos(\alpha), \cos(\beta), \cos(\gamma)> \\ \Rightarrow& \frac{\mathbf{a}}{|\mathbf{a}|} = <\cos(\alpha), \cos(\beta), \cos(\gamma)>\end{align*}$$
즉, 벡터 $\mathbf{a}$의 방향각이라는 것은 $\mathbf{a}$의 단위벡터가 각 축과 이루는 각도를 의미합니다.
예제1. 벡터 $\mathbf{a} = <1, 2, 3>$의 방향각을 구하여라.
$$\begin{align*} &\cos(\alpha) = \frac{a_{1}}{|\mathbf{a}|} = \frac{1}{\sqrt{14}} \Rightarrow \alpha = \arccos(\frac{1}{\sqrt{14}}) \\ &\cos(\beta) = \frac{a_{2}}{|\mathbf{a}|} = \frac{2}{\sqrt{14}} \Rightarrow \beta = \arccos(\frac{2}{\sqrt{14}}) \\ &\cos(\gamma) = \frac{a_{3}}{|\mathbf{a}|} = \frac{3}{\sqrt{14}} \Rightarrow \gamma = \arccos(\frac{3}{\sqrt{14}})\end{align*}$$
정의2. 사영(projection)
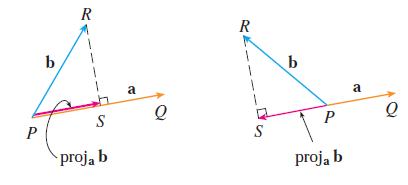
동일한 시점(initial point)를 공유하는 두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 있다고 가정하자. 이때, 점 $S$를 벡터 $\vec{PQ}$ 상에 점 $R$과 수직을 이루는 수선의 발이라고 하자. 그러면, 벡터 $\vec{PS}$를 $\mathbf{b}$의 $\mathbf{a}$로의 사영(vector projection of $\mathbf{b}$ onto $\mathbf{a}$)이라고 하고 $\text{proj}_{\mathbf{a}} \mathbf{b}$로 표기한다.
$$\text{proj}_{\mathbf{a}} \mathbf{b} = \left(\frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|}\right) \frac{\mathbf{a}}{|\mathbf{a}|} = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|^{2}} \mathbf{a}$$
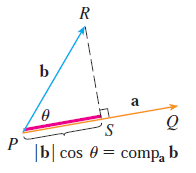
여기서, 사영벡터 $\text{proj}_{\mathbf{a}} \mathbf{b}$의 길이를 스칼라 사영(scalar projection) 또는 성분(component)라고 하고 $\text{comp}_{\mathbf{a}} \mathbf{b}$로 표기한다.
$$\text{comp}_{\mathbf{a}} \mathbf{b} = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}|}$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 3차원 직선과 평면의 방정식 (0) | 2022.05.25 |
|---|---|
| 미적분학 - 벡터의 외적 (1) | 2022.05.24 |
| 미적분학 - 벡터의 내적 (0) | 2022.05.21 |
| 미적분학 - 벡터의 성분 (0) | 2022.05.20 |
| 미적분학 - 벡터 (0) | 2022.05.18 |
