안녕하세요. 지난 포스팅의 미적분학 - 극좌표계 적분에서는 극좌표계에서 적분하는 방법에 대해서 알아보았습니다. 오늘은 잠깐 기하학으로 주제를 바꾸어 원뿔에 대해서 간단하게 알아보도록 하겠습니다.
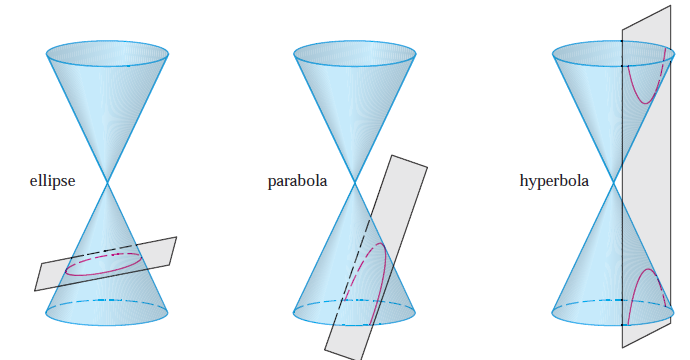
위와 같은 원뿔의 신기한 성질 중 하나는 자르는 평면에 따라서 다양한 2차원 곡선을 얻을 수 있다는 것입니다. 예를 들어보겠습니다. 왼쪽 그림과 같이 밑면에 대해 비스듬하게 자르면 타원을 얻고 중간 그림과 같이 수직면에 대해서 비스듬하게 자르면 포물선, 오른쪽 그림과 같이 밑면에 수직으로 자르면 쌍곡선을 얻을 수 있습니다. 오늘은 각 기하곡선에 대한 정의를 알아보도록 하겠습니다.
정의1. 포물선(Parabola)
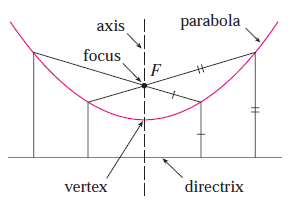
포물선은 고정점(fixed point) 또는 초점(focus) $F$로부터 동일한 길이의 준선(directrix)을 가지는 점의 자취이다.
설명
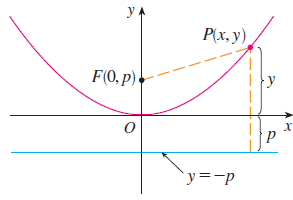
위의 그림을 보시면 더욱 쉽게 이해하실 수 있습니다. 포물선을 그릴 때 중요한 것은 초점 $F$와 준선입니다. 그리고 해당 포물선을 모델링하기 위해서 수학적으로 셋팅해보도록 하겠습니다. 위의 포물선을 직교좌표 위에 올려두도록 하겠습니다. 이때, 초점은 $y$ 축 상에 놓이도록 합니다. 그러면 임의의 양수 $p$에 대해서 초점의 위치는 $F(0, p)$가 됩니다. 그리고 원점이 포물선에서 가장 낮은 위치라고 한다면 포물선의 정의에 의해서 준선은 $y = -p$가 되어야 $\left|OP\right| = p$가 될 수 있습니다.
다음으로 할 것은 포물선의 임의의 점을 $P(x, y)$라고 하겠습니다. 이때, 포물선의 정의를 통해 $\bar{PF} = \left|y + p\right|$임을 알 수 있습니다. 여기서 점과 점 사이의 거리 공식을 이용하면 아래와 같이 방정식을 만들 수 있습니다.
$$\begin{align*} \sqrt{x^{2} + (y - p)^{2}} = \left|y + p\right| &\Rightarrow x^{2} + (y - p)^{2} = (y + p)^{2} \\ &\Rightarrow x^{2} + y^{2} - 2py + p^{2} = y^{2} + 2py + p^{2} \\ &\Rightarrow x = 4py \end{align*}$$

그리고 이 포물선들은 위의 모양에 따라 다르게 모델링 됩니다.
정의2. 타원(Ellipses)
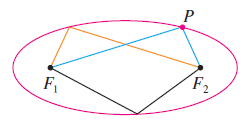
타원은 초점 $F_{1}$과 점 $P$, 그리고 $F_{2}$와 $P$ 사이의 거리의 합이 일정한 모든 점의 자취이다.
설명
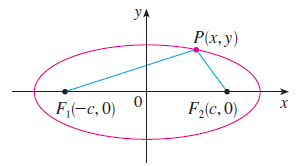
위의 그림을 보시면 타원도 쉽게 이해할 수 있습니다. 먼저, 위의 타원을 직교좌표 위에 올려두도록 하겠습니다. 이때, 각 초점을 $F_{1}(-c, 0)$ 그리고 $F_{2}(c, 0)$이라고 하겠습니다. 여기서, 타원의 정의에 의해서 임의의 양수 $a$에 대해서 $\left|F_{1}P\right| + \left|F_{2}P\right| = 2a$라고 쓸 수 있습니다. 그러면 두 점 사이의 거리 공식을 통해 아래와 같이 쓸 수 있습니다. 주의할 점은 위의 그림에서 $c > a$라는 것을 알 수 있다는 것입니다.
$$\begin{align*} \sqrt{(x + c)^{2} + y^{2}} + \sqrt{(x - c)^{2} + y^{2}} = 2a &\Rightarrow \sqrt{(x - c)^{2} + y^{2}} = 2a - \sqrt{(x + c)^{2} + y^{2}} \\ &\Rightarrow (x - c)^{2} + y^{2} = 4a^{2} - 4a\sqrt{(x + c)^{2} + y^{2}} + (x + c)^{2} + y^{2} \\ &\Rightarrow x^{2} - 2cx + c^{2} + y^{2} = 4a^{2} - 4a\sqrt{(x + c)^{2} + y^{2}} + x^{2} + 2cx + c^{2} + y^{2} \\ &\Rightarrow a\sqrt{(x + c)^{2} + y^{2}} = a^{2} + cx \\ &\Rightarrow a^{2}\left[(x +c)^{2} + y^{2}\right]^{2} = \left[a^{2} + cx\right]^{2} \\ &\Rightarrow a^{2}(x^{2} +2cx + c^{2} + y^{2}) = a^{4} + 2a^{2}cx + c^{2}x^{2} \\ &\Rightarrow (a^{2} - c^{2})x^{2} + a^{2}y^{2} = a^{2}(a^{2} - c^{2}) \\ &\Rightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\end{align*}$$
이때, $b^{2} = a^{2} - c^{2} > 0$입니다.
정의3. 쌍곡선(Hyperbola)
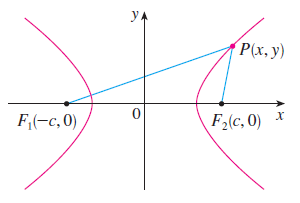
쌍곡선은 초점 $F_{1}$과 점 $P$, 그리고 $F_{2}$와 $P$ 사이의 거리의 차이가 일정한 모든 점의 자취이다.
설명
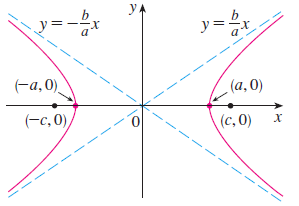
위의 그림을 보시면 쌍곡선도 쉽게 이해할 수 있습니다. 먼저, 위의 쌍곡선을 직교좌표 위에 올려두도록 하겠습니다. 이때, 각 초점을 $F_{1}(-c, 0)$ 그리고 $F_{2}(c, 0)$이라고 하겠습니다. 여기서, 쌍곡선의 정의에 의해서 임의의 양수 $a$에 대해서 $\left|F_{1}P\right| - \left|F_{2}P\right| =\pm 2a$라고 쓸 수 있습니다. 그러면 두 점 사이의 거리 공식을 통해 아래와 같이 쓸 수 있습니다.
$$\begin{align*} \sqrt{(x + c)^{2} + y^{2}} - \sqrt{(x - c)^{2} + y^{2}} = 2a &\Rightarrow \sqrt{(x + c)^{2} + y^{2}} = 2a + \sqrt{(x - c)^{2} + y^{2}} \\ &\Rightarrow (x + c)^{2} + y^{2} = \left[2a + \sqrt{(x - c)^{2} + y^{2}}\right]^{2} \\ &\Rightarrow x^{2} + 2cx + c^{2} + y^{2} = 4a^{2} + 4a\sqrt{(x - c)^{2} + y^{2}} + (x - c)^{2} + y^{2} \\ &\Rightarrow x^{2} + 2cx + c^{2} + y^{2} = 4a^{2} + 4a\sqrt{(x - c)^{2} + y^{2}} + x^{2} - 2cx + c^{2} + y^{2} \\ &\Rightarrow cx = a^{2} + a\sqrt{(x - c)^{2} + y^{2}} \\ &\Rightarrow cx - a^{2} = a\sqrt{(x - c)^{2} + y^{2}} \\ &\Rightarrow (cx - a^{2})^{2} = a^{2}((x - c)^{2} + y^{2}) \\ &\Rightarrow c^{2}x^{2} - 2a^{2}cx + a^{4} = a^{2}(x^{2} - 2cx + c^{2} + y^{2}) \\ &\Rightarrow c^{2}x^{2} - 2a^{2}cx + a^{4} = a^{2}x^{2} - 2a^{2}cx + a^{2}c^{2} + a^{2}y^{2} \\ &\Rightarrow (c^{2} - a^{2})x^{2} - a^{2}y^{2} = a^{2}(c^{2} - a^{2}) \\ &\Rightarrow \frac{x^{2}}{a^{2}} - \frac{y}{b^{2}} = 1\end{align*}$$
이때, $b^{2} = c^{2} - a^{2} > 0$입니다.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 수열 (0) | 2022.04.21 |
|---|---|
| 미적분학 - 극좌표계와 원뿔 단면 곡선 (0) | 2022.04.19 |
| 미적분학 - 극좌표계 미분과 적분 (0) | 2022.04.10 |
| 미적분학 - 극좌표계 곡선 (0) | 2022.04.09 |
| 미적분학 - 극좌표계 (0) | 2022.04.08 |
