안녕하세요. 지난 포스팅의 미적분학 - 원뿔 단면에서는 3차원 원뿔을 다양한 방식으로 잘랐을 때 얻어지는 곡선들과 함께 정의를 통해 대수적으로 표현하는 방법까지 알아보았습니다. 각각 타원, 포물선, 쌍곡선을 보았죠. 오늘은 이들을 극좌표계에서 표현해보도록 하겠습니다. 시작하기에 앞서 곡선들과 관련된 흥미로운 이론을 하나 소개해드리겠습니다.
정리1.
$F$를 초점(focust), $I$를 준선(directrix)라고 하자. 이때, $e$를 고정된 양수을 가지는 이심률(eccentricity)를 아래와 같이 정의한다.
$$e = \frac{\left|PF\right|}{\left|PI\right|}$$
그러면 $e < 1$이면 타원(ellipse), $e = 1$이면 포물선(parabola), $e > 1$이면 쌍곡선(hyperbola)이다.
증명
1). $e = 1$이라고 가정하면 이심률의 정의에 의해서 $\left|PF\right| = \left|PI\right|$이다. 이는 포물선의 정의와 일치하므로 $e = 1$이라면 포물선이다.
2).
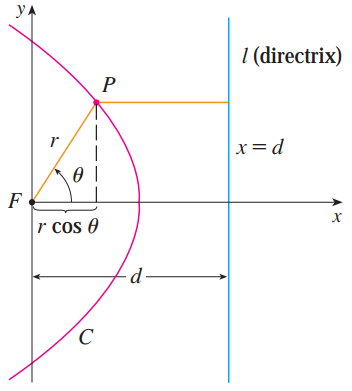
좀 더 일반적인 경우를 증명하기 위해 극좌표계를 사용하여 위와 같은 그림을 고려한다. 그러면, $\left|PF\right| = r$ 이고 $\left|PI\right| = d - r\cos(\theta)$이다. 이때, 이심률의 정의에 의해 아래와 같이 쓸 수 있다.
$$e = \frac{\left|PF\right|}{\left|PI\right|} \Rightarrow \left|PF\right| = e\left|PI\right| \Rightarrow r = e(d - r\cos(\theta))$$
여기서, 극좌표계를 직교좌표계로 변환한다.
$$x^{2} + y^{2} = e^{2}(d - x)^{2} = e^{2}(d^{2} - 2dx + x^{2}) \Rightarrow (1 - e^{2})x^{2} + 2de^{2}x + y^{2} = e^{2}d^{2}$$
또는 완전제곱식의 형태로 아래와 같이 쓸 수 있다.
$$\left(x + \frac{e^{2}d}{1 - e^{2}}\right)^{2} + \frac{y^{2}}{1 - e^{2}} = \frac{e^{2}d^{2}}{(1 - e^{2})^{2}}$$
이때, $e < 1$라고 하면 $h = -\frac{e^{2}d}{1 - e^{2}}, a^{2} = \frac{e^{2}d^{2}}{(1 - e^{2})^{2}}, b^{2} = \frac{e^{2}d^{2}}{1 - e^{2}}$이라고 할 때, 아래와 같이 쓸 수 있다.
$$\frac{(x - h)^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$$
$e > 1$일 때도 마찬가지로 쌍곡선으로 표현할 수 있다.
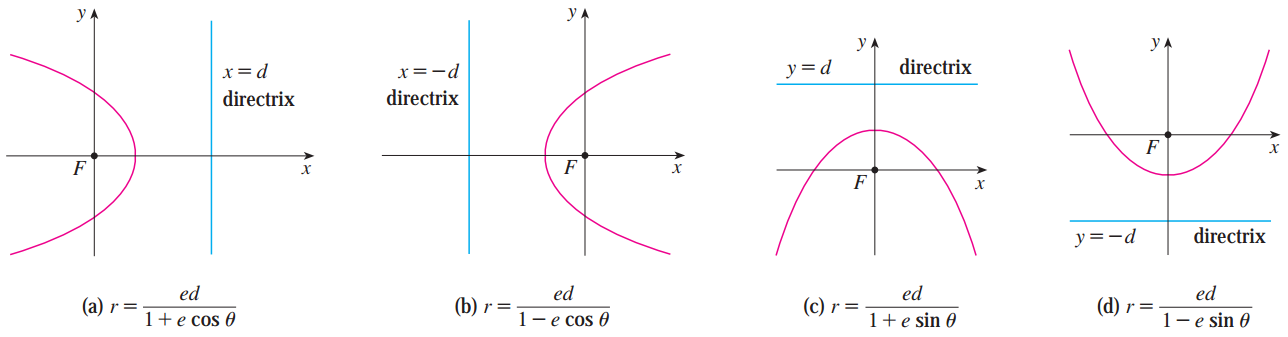
결론적으로 위 정리의 증명 과정에서 이미 극좌표계에서 곡선들을 표현할 수 있는 방법을 유도할 수 있습니다.
$$r = e(d - r\cos(\theta)) \Rightarrow r = \frac{ed}{1 + e\cos(\theta)}$$
위 수식은 가장 오른쪽 그림의 형태입니다. 따라서 모든 형태의 곡선은 아래의 4개의 식 중 하나로 표현할 수 있습니다.
$$r = \frac{ed}{1 \pm e\cos(\theta)}$$
$$r = \frac{ed}{1 \pm e\sin(\theta)}$$
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 수열 극한의 법칙 (2) | 2022.04.24 |
|---|---|
| 미적분학 - 수열 (0) | 2022.04.21 |
| 미적분학 - 원뿔 단면 (0) | 2022.04.14 |
| 미적분학 - 극좌표계 미분과 적분 (0) | 2022.04.10 |
| 미적분학 - 극좌표계 곡선 (0) | 2022.04.09 |
안녕하세요. 지난 포스팅의 미적분학 - 원뿔 단면에서는 3차원 원뿔을 다양한 방식으로 잘랐을 때 얻어지는 곡선들과 함께 정의를 통해 대수적으로 표현하는 방법까지 알아보았습니다. 각각 타원, 포물선, 쌍곡선을 보았죠. 오늘은 이들을 극좌표계에서 표현해보도록 하겠습니다. 시작하기에 앞서 곡선들과 관련된 흥미로운 이론을 하나 소개해드리겠습니다.
정리1.
F를 초점(focust), I를 준선(directrix)라고 하자. 이때, e를 고정된 양수을 가지는 이심률(eccentricity)를 아래와 같이 정의한다.
e=|PF||PI|
그러면 e<1이면 타원(ellipse), e=1이면 포물선(parabola), e>1이면 쌍곡선(hyperbola)이다.
증명
1). e=1이라고 가정하면 이심률의 정의에 의해서 |PF|=|PI|이다. 이는 포물선의 정의와 일치하므로 e=1이라면 포물선이다.
2).

좀 더 일반적인 경우를 증명하기 위해 극좌표계를 사용하여 위와 같은 그림을 고려한다. 그러면, |PF|=r 이고 |PI|=d−rcos(θ)이다. 이때, 이심률의 정의에 의해 아래와 같이 쓸 수 있다.
e=|PF||PI|⇒|PF|=e|PI|⇒r=e(d−rcos(θ))
여기서, 극좌표계를 직교좌표계로 변환한다.
x2+y2=e2(d−x)2=e2(d2−2dx+x2)⇒(1−e2)x2+2de2x+y2=e2d2
또는 완전제곱식의 형태로 아래와 같이 쓸 수 있다.
(x+e2d1−e2)2+y21−e2=e2d2(1−e2)2
이때, e<1라고 하면 h=−e2d1−e2,a2=e2d2(1−e2)2,b2=e2d21−e2이라고 할 때, 아래와 같이 쓸 수 있다.
(x−h)2a2+y2b2=1
e>1일 때도 마찬가지로 쌍곡선으로 표현할 수 있다.
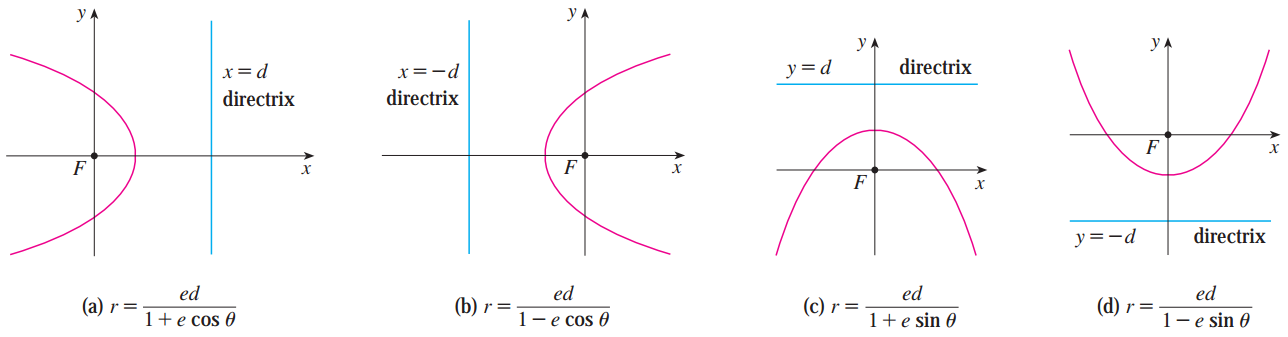
결론적으로 위 정리의 증명 과정에서 이미 극좌표계에서 곡선들을 표현할 수 있는 방법을 유도할 수 있습니다.
r=e(d−rcos(θ))⇒r=ed1+ecos(θ)
위 수식은 가장 오른쪽 그림의 형태입니다. 따라서 모든 형태의 곡선은 아래의 4개의 식 중 하나로 표현할 수 있습니다.
r=ed1±ecos(θ)
r=ed1±esin(θ)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 수열 극한의 법칙 (2) | 2022.04.24 |
|---|---|
| 미적분학 - 수열 (0) | 2022.04.21 |
| 미적분학 - 원뿔 단면 (0) | 2022.04.14 |
| 미적분학 - 극좌표계 미분과 적분 (0) | 2022.04.10 |
| 미적분학 - 극좌표계 곡선 (0) | 2022.04.09 |
