안녕하세요. 지난 포스팅의 미적분학 - 수열에서는 수열의 정의와 일반항을 구하는 방법에 대해서 알아보았습니다. 또한, 극한에 대한 정확한 정의도 알아보았었죠. 오늘은 함수 극한과 마찬가지로 수열 극한도 몇 가지 법칙이 존재하는데요, 이를 알아보도록 하겠습니다.
일단, $\lim_{n \rightarrow \infty} a_{n}$과 $\lim_{n \rightarrow \infty} b_{n}$이 존재한다고 가정하면 아래의 법칙들이 성립합니다.
- $\lim_{n \rightarrow \infty} \left[a_{n} \pm b_{n}\right] = \lim_{n \rightarrow \infty} a_{n} \pm \lim_{n \rightarrow \infty} b_{n}$
- $\lim_{n \rightarrow \infty} \left[ca_{n}\right] = c\lim_{n \rightarrow \infty} a_{n}$
- $\lim_{n \rightarrow \infty} \left[a_{n} \cdot b_{n}\right] = \left[\lim_{n \rightarrow \infty} a_{n}\right] \cdot \left[\lim_{n \rightarrow \infty} b_{n}\right]$
- $\lim_{n \rightarrow \infty} \frac{a_{n}}{b_{n}} = \frac{\lim_{n \rightarrow \infty} a_{n}}{\lim_{n \rightarrow \infty} b_{n}}$(이때, $\lim_{n \rightarrow b_{n}} \neq 0$ 이여야 합니다!)
- $\lim_{n \rightarrow \infty} \left[a_{n} \right]^{n} = \left[\lim_{n \rightarrow \infty} a_{n} \right]^{n}$
- $\lim_{n \rightarrow \infty} c = c$
- $\lim_{n \rightarrow \infty} \sqrt[n]{a_{n}} = \sqrt[n]{\lim_{n \rightarrow \infty} a_{n}}$
정리1. 샌드위치 정리(Squeeze Theorem)
충분히 큰 $n \ge n_{0}$에 대해서 $a_{n} \le b_{n} \le c_{n}$이고 $\lim_{n \rightarrow \infty} a_{n} = \lim_{n \rightarrow \infty} c_{n} = L$이면 $\lim_{n \rightarrow \infty} b_{n} = L$이다.
설명
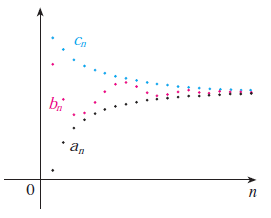
샌드위치 정리를 그림으로 그려보면 위와 같이 그릴 수 있습니다. $b_{n}$은 두 수열 $a_{n}$과 $c_{n}$ 사이에 껴서 점점 한 곳으로 수렴하는 것을 볼 수 있습니다.
정리2.
$\lim_{n \rightarrow \infty} \left|a_{n}\right| = 0$이면 $\lim_{n \rightarrow \infty} a_{n} = 0$이다.
예제1. $\lim_{n \rightarrow \infty} \frac{n}{n + 1}$의 극한을 구하라.
$$\begin{align*} \lim_{n \rightarrow \infty} \frac{n}{n + 1} &= \lim_{n \rightarrow \infty} \frac{1}{1 + \frac{1}{n}} \\ &= \frac{1}{1 + 0} = 1\end{align*}$$
예제2. $\lim_{n \rightarrow \infty} (-1)^{n}$의 극한을 구하라.
$a_{n} = (-1)^{n}$이라고 할 때, $\{a_{n}\} = \{-1, 1, -1, 1, \dots, \}$이기 때문에 수렴하지 않고 발산(진동)한다.
예제3. $\lim_{n \rightarrow \infty} \frac{(-1)^{n}}{n}$의 극한을 구하라.
$a_{n} = \frac{(-1)^{n}}{n}$이라고 할 때, $\lim_{n \rightarrow \infty} \left|a_{n}\right| = \lim_{n \rightarrow \infty} \frac{1}{n} = 0$이다. 정리2에 의해서 $\lim_{n \rightarrow \infty} \frac{(-1)^{n}}{n} = 0$이다.
정리3.
$\lim_{n \rightarrow \infty} a_{n} = L$이고 함수 $f$가 $x = L$에서 연속이면 $\lim_{n \rightarrow \infty} f(a_{n}) = f(L)$이다.
예제4. $\lim_{n \rightarrow \infty} \sin\left(\frac{\pi}{n}\right)$의 극한을 구하라.
$\sin$ 함수는 전 구간에서 연속이기 때문에 정리3에 의해서 $\lim_{n \rightarrow \infty} \sin\left(\frac{\pi}{n}\right) = \sin(0) = 0$이다.
정의1. 증가수열(increasing sequence)과 감소수열(decreasing sequence)
수열 $\{a_{n}\}$이 모든 $n$에 대해서 $a_{n + 1} > a_{n}$이라면 증가수열, $a_{n + 1} < a_{n}$이라면 감소수열이라고 한다.
정의2. 유계 수열(bounded sequence)
수열 $\{a_{n}\}$이 모든 $n$에 대해서 $a_{n} \le M$를 만족하는 $M$이 존재하면 위로 유계(bounded above)이고 $a_{n} \ge m$을 만족하는 $m$이 존재하면 아래로 유계(bounded below)라고 한다. 만약, 수열 $\{a_{n}\}$이 위로 또는 아래로 유계라면 유계 수열(bounded sequence)라고 한다.
정리4. 단조 수열 정리
임의의 유계 단조 수열을 수렴한다.
연습문제1. 주어진 수열이 증감수열인지 또는 둘다 아닌지 판단하라.
(a). $a_{n} = (-2)^{n + 1}$
(b). $a_{n} = \frac{1}{2n + 3}$
(c). $a_{n} = n(-1)^{n}$
(d). $a_{n} = ne^{-n}$
(e). $a_{n} = \frac{n}{n^{2} + 1}$
(f). $a_{n} = n + \frac{1}{n + 1}$
(a). $a_{n} = (-2)^{n + 1}$ Not Monotonic
해당 수열 $a_{n}$은 홀수항에서 양수이고 짝수항에서 음수로 진동하는 수열이기 때문에 증가수열과 감소수열에 모두 속하지 않는다.
(b). $a_{n} = \frac{1}{2n + 3}$ Decreasing Sequence
$$\begin{align*} a_{n + 1} &= \frac{1}{2(n + 1) + 3} \\ &= \frac{1}{2n + 5} \\ &< \frac{1}{2n + 3} = a_{n} \end{align*}$$
모든 $n \in \mathbb{N}$에 대해서 $a_{n} > a_{n + 1}$이기 때문에 감소수열이다.
(c). $a_{n} = n(-1)^{n}$ Not Monotonic
(a)와 유사하게 해당 수열 $a_{n}$은 홀수항에서 음수이게 짝수항에서 양수로 진동하는 수열이기 때문에 증가수열과 감소수열 모두 속하지 않는다.
(d). $a_{n} = ne^{-n}$ Decreasing Sequence
$f(x) = xe^{-x}$라고 하자. 그러면 도함수 $f^{'}(x) = e^{-x} - xe^{-x} = (1 - x)e^{-x}$를 얻을 수 있다. 이때, 모든 $x \ge 1$에 대해서 $e^{-x} > 0$이기 때문에 $f^{'}(x) < 0$이다. 따라서, 함수 $f$는 $[1, \infty)$에서 감소함수이므로 $n \in \mathbb{N}$에 대해서 $a_{n} = f(n) > f(n + 1) = a_{n + 1}$을 만족하여 $a_{n}$은 감소수열이다.
(e). $a_{n} = \frac{n}{n^{2} + 1}$ Decreasing Sequence
$f(x) = \frac{x}{x^{2} + 1}$라고 하자. 그러면 도함수 $f^{'}(x) = \frac{(x^{2} + 1) - 2x^{2}}{(x^{2} + 1)^{2}} = \frac{-x^{2} + 1}{(x^{2} + 1)^{2}}$를 얻을 수 있다. 이때, 모든 $x \ge 1$에 대해서 $(x^{2} + 1)^{2} > 0$이기 때문에 $f^{'}(x) < 0$이다. 따라서, 함수 $f$는 $[1, \infty)$에서 감소함수이므로 $n \in \mathbb{N}$에 대해서 $a_{n} = f(n) > f(n + 1) = a_{n + 1}$을 만족하여 $a_{n}$은 감소수열이다.
(f). $a_{n} = n + \frac{1}{n + 1}$ Increasing Sequence
$f(x) = x + \frac{1}{x + 1}$라고 하자. 그러면 도함수 $f^{'}(x) = 1 - \frac{1}{(x + 1)^{2}}$를 얻을 수 있다. 이때, 모든 $x \ge 1$에 대해서 $f^{'}(x) > 0$이다. 따라서, 함수 $f$는 $[1, \infty)$에서 증가함수이므로 $n \in \mathbb{N}$에 대해서 $a_{n} = f(n) < f(n + 1) = a_{n + 1}$을 만족하여 $a_{n}$은 증가수열이다.
연습문제2. 수열 $a_{n + 1} = \sqrt{2 + a_{n}}$이 초항 $a_{1} = \sqrt{2}$으로 정의되었을 때 수열 $\{ a_{n} \}$은 증가수열이면서 3에 유계임을 증명하고 $a_{n}$의 극한값을 구하여라.
STEP1. 수열 $\{ a_{n} \}$은 증가수열이다.
수열 $\{ a_{n} \}$이 증가수열임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자. 수열 $\{ a_{n} \}$이 증가수열이라는 것은 모든 $n \in \mathbb{N}$에 대해서 $a_{n} < a_{n + 1}$인 것과 동치이다.
1) $n = 1$인 경우 $a_{1} = \sqrt{2}$이고 $a_{2} = \sqrt{2 + \sqrt{2}}$이므로 $a_{1} < a_{2}$이다.
2) $n = k - 1$에 대해서 $a_{k - 1} < a_{k}$이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $a_{k} < a_{k + 1}$임을 증명하면 된다.
$$\begin{align*} a_{k + 1} &= \sqrt{2 + a_{k}} \\ &> \sqrt{2 + a_{k - 1}} = a_{k} \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $a_{n + 1} > a_{n}$이므로 수열 $\{ a_{n} \}$은 증가수열이다.
STEP2. 수열 $\{ a_{n} \}$은 3에 유계이다.
수열 $\{ a_{n} \}$은 3에 유계수열임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자. 수열 $\{ a_{n} \}$이 3에 유계수열이라는 것은 모든 $n \in \mathbb{N}$에 대해서 $a_{n} \le 3$인 것과 동치이다.
1) $n = 1$인 경우 $a_{1} = \sqrt{2} < 3$이다.
2) $n = k - 1$에 대해서 $a_{k - 1} \le 3$이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $a_{k} \le 3$임을 증명하면 된다.
$$\begin{align*} a_{k} = \sqrt{2 + a_{k - 1}} \le \sqrt{2 + 3} = \sqrt{5} < 3 \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $a_{n} \le 3$이므로 수열 $\{ a_{n} \}$은 3에 유계이다.
STEP3. $\lim_{n \rightarrow \infty} a_{n}$
STEP1과 STEP2에 의해 수열 $\{ a_{n} \}$은 증가수열이며 상한선으로 3에 유계되어있음이 증명되었으므로 정리4. 유계단조정리에 의해 수열 $\{ a_{n} \}$의 극한은 수렴한다.
$\lim_{n \rightarrow \infty} a_{n} = L$이라고 할 때 $\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} a_{n}$임 (미적분학 - 수열 연습문제8)을 이용하여 수열 $a_{n + 1} = \sqrt{2 + a_{n}}$의 양변에 $n \rightarrow \infty$으로의 극한을 취해주면 된다.
$$\begin{align*} &\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} \sqrt{2 + a_{n}} \\ &\Rightarrow L = \sqrt{2 + \sqrt{L}} \\ &\Rightarrow (L - 2)(L + 1) = 0 \end{align*}$$
이때, $a_{1} = \sqrt{2}$이고 수열 $\{ a_{n} \}$은 증가수열이므로 $L = 2$이다.
연습문제3. 수열 $a_{n + 1} = 3 - \frac{1}{a_{n}}$이 초항 $a_{1} = 1$으로 정의되었을 때 수열 $\{ a_{n} \}$은 증가수열이면서 3에 유계임을 증명하고 $a_{n}$의 극한값을 구하여라.
STEP1. 수열 $\{ a_{n} \}$은 증가수열이다.
수열 $\{ a_{n} \}$이 증가수열임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자. 수열 $\{ a_{n} \}$이 증가수열이라는 것은 모든 $n \in \mathbb{N}$에 대해서 $a_{n} < a_{n + 1}$인 것과 동치이다.
1) $n = 1$인 경우 $a_{1} = 1$이고 $a_{2} = 3 - 1 = 2$이므로 $a_{1} < a_{2}$이다.
2) $n = k - 1$에 대해서 $a_{k - 1} < a_{k}$이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $a_{k} < a_{k + 1}$임을 증명하면 된다.
$$\begin{align*} a_{k + 1} &= 3 - \frac{1}{a_{k}} \\ &> 3 - \frac{1}{a_{k - 1}} = a_{k} \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $a_{n + 1} > a_{n}$이므로 수열 $\{ a_{n} \}$은 증가수열이다.
STEP2. 수열 $\{ a_{n} \}$은 3에 유계이다.
수열 $\{ a_{n} \}$은 3에 유계수열임을 증명하기 위해 귀류법 (Proof by Contradiction)을 이용하자. 즉, $\{ a_{n} \}$은 3에 유계수열이 아니라고 가정하자. 이는 어떤 $n \in \mathbb{N}$에 대해서 $a_{n} > 3$을 만족하는 것과 동치가 된다. 하지만 $a_{k} = 3 - \frac{1}{a_{k - 1}} > 3 \Rightarrow a_{k - 1} < 0$이 되므로 STEP1에서 얻었던 수열 $\{ a_{n} \}$은 증가수열인 것과 $a_{1} = 1$인 것과 서로 모순된다. 따라서, 귀류법에 의해 수열 $\{ a_{n} \}$은 3에 유계이다.
STEP3. $\lim_{n \rightarrow \infty} a_{n}$
STEP1과 STEP2에 의해 수열 $\{ a_{n} \}$은 증가수열이며 상한선으로 3에 유계되어있음이 증명되었으므로 정리4. 유계단조정리에 의해 수열 $\{ a_{n} \}$의 극한은 수렴한다.
$\lim_{n \rightarrow \infty} a_{n} = L$이라고 할 때 $\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} a_{n}$임 (미적분학 - 수열 연습문제8)을 이용하여 수열 $a_{n + 1} = 3 - \frac{1}{a_{n}}$의 양변에 $n \rightarrow \infty$으로의 극한을 취해주면 된다.
$$\begin{align*} &\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} \left( 3 - \frac{1}{a_{n}} \right) \\ &\Rightarrow L = 3 - \frac{1}{L} \\ &\Rightarrow L^{2} - 3L + 1 = 0 \\ &\Rightarrow L = \frac{3 \pm \sqrt{5}}{2} \end{align*}$$
이때, $a_{1} = 1$이고 수열 $\{ a_{n} \}$은 증가수열이므로 $L = \frac{3 + \sqrt{5}}{2}$이다.
연습문제4. 수열 $a_{n + 1} = \frac{1}{3 - a_{n}}$이 초항 $a_{1} = 2$으로 정의되었을 때 수열 $\{ a_{n} \}$은 감소수열이면서 모든 $n \in \mathbb{N}$에 대해서 $0 < a_{n} \le 2$임을 증명하고 $a_{n}$의 극한값을 구하여라.
STEP1. 모든 $n \in \mathbb{N}$에 대해서 $0 < a_{n} \le 2$이다.
모든 $n \in \mathbb{N}$에 대해서 $0 < a_{n} \le 2$임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자.
1) $n = 1$인 경우 $a_{1} = 2$이므로 $0 < a_{1} = 2 \le 2$를 만족한다.
2) $n = k - 1$에 대해서 $0 < a_{k - 1} \le 2$ 이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $0 < a_{k} \le 2$ 임을 증명하면 된다. 이때, 수학적 귀납법의 가정에 의해 다음과 같이 식을 전개할 수 있다.
$$\begin{align*} &0 < a_{k - 1} \le 2 \\ &\Rightarrow -2 \le -a_{k - 1} < 0 \\ &\Rightarrow 1 \le 3 - a_{k - 1} < 3 \\ &\Rightarrow 0 < \frac{1}{3} \le \frac{1}{3 - a_{k - 1}} = a_{k} < 1 < 2 \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $0 < a_{n} \le 2$이다.
STEP2. 수열 $\{ a_{n} \}$은 감소수열이다.
수열 $\{ a_{n} \}$이 감소수열임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자. 수열 $\{ a_{n} \}$이 감소수열이라는 것은 모든 $n \in \mathbb{N}$에 대해서 $a_{n} > a_{n + 1}$인 것과 동치이다.
1) $n = 1$인 경우 $a_{1} = 2$이고 $a_{2} = \frac{1}{3 - a_{1}} = 1$이므로 $a_{1} > a_{2}$이다.
2) $n = k - 1$에 대해서 $a_{k - 1} > a_{k}$이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $a_{k} > a_{k + 1}$임을 증명하면 된다.
$$\begin{align*} a_{k + 1} &= \frac{1}{3 - a_{k}} \\ &< \frac{1}{3 - a_{k - 1}} = a_{k} \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $a_{n + 1} < a_{n}$이므로 수열 $\{ a_{n} \}$은 감소수열이다.
STEP3. $\lim_{n \rightarrow \infty} a_{n}$
STEP1과 STEP2에 의해 수열 $\{ a_{n} \}$은 감소수열이며 하한선으로 0에 유계되어있음이 증명되었으므로 정리4. 유계단조정리에 의해 수열 $\{ a_{n} \}$의 극한은 수렴한다.
$\lim_{n \rightarrow \infty} a_{n} = L$이라고 할 때 $\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} a_{n}$임 (미적분학 - 수열 연습문제8)을 이용하여 수열 $a_{n + 1} = \frac{1}{3 - a_{n}}$의 양변에 $n \rightarrow \infty$으로의 극한을 취해주면 된다.
$$\begin{align*} &\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} \frac{1}{3 - a_{n}} \\ &\Rightarrow L = \frac{1}{3 - L} \\ &\Rightarrow L(L - 3) = 0 \end{align*}$$
이때, $a_{1} = 2$이고 수열 $\{ a_{n} \}$은 감소수열이므로 $L = 0$이다.
연습문제5. $\lim_{n \rightarrow \infty} a_{n} = 0$이고 수열 $\{ b_{n} \}$이 유계일 때 $\lim_{n \rightarrow \infty} a_{n}b_{n} = 0$임을 증명하라.
Since the sequence $\{ b_{n} \}$ is bounded, there exists $M \in \mathbb{R}$ such that $| b_{n} | \le M$ for all $n \in \mathbb{N}$. Additionally, since $\lim_{n \rightarrow \infty} a_{n} = 0$, for given $\epsilon > 0$, there exists $n \le N$ such that $|a_{n}| < \frac{\epsilon}{M}$.
Consequently, if $n \ge N$, $|a_{n}b_{n} - 0| = |a_{n}b_{n}| = |a_{n}||b_{n}| < \frac{\epsilon}{M} \cdot M = \epsilon$.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 무한급수의 수렴성 검사 1 (0) | 2022.05.05 |
|---|---|
| 미적분학 - 급수 (0) | 2022.04.28 |
| 미적분학 - 수열 (0) | 2022.04.21 |
| 미적분학 - 극좌표계와 원뿔 단면 곡선 (0) | 2022.04.19 |
| 미적분학 - 원뿔 단면 (0) | 2022.04.14 |
안녕하세요. 지난 포스팅의 미적분학 - 수열에서는 수열의 정의와 일반항을 구하는 방법에 대해서 알아보았습니다. 또한, 극한에 대한 정확한 정의도 알아보았었죠. 오늘은 함수 극한과 마찬가지로 수열 극한도 몇 가지 법칙이 존재하는데요, 이를 알아보도록 하겠습니다.
일단, $\lim_{n \rightarrow \infty} a_{n}$과 $\lim_{n \rightarrow \infty} b_{n}$이 존재한다고 가정하면 아래의 법칙들이 성립합니다.
- $\lim_{n \rightarrow \infty} \left[a_{n} \pm b_{n}\right] = \lim_{n \rightarrow \infty} a_{n} \pm \lim_{n \rightarrow \infty} b_{n}$
- $\lim_{n \rightarrow \infty} \left[ca_{n}\right] = c\lim_{n \rightarrow \infty} a_{n}$
- $\lim_{n \rightarrow \infty} \left[a_{n} \cdot b_{n}\right] = \left[\lim_{n \rightarrow \infty} a_{n}\right] \cdot \left[\lim_{n \rightarrow \infty} b_{n}\right]$
- $\lim_{n \rightarrow \infty} \frac{a_{n}}{b_{n}} = \frac{\lim_{n \rightarrow \infty} a_{n}}{\lim_{n \rightarrow \infty} b_{n}}$(이때, $\lim_{n \rightarrow b_{n}} \neq 0$ 이여야 합니다!)
- $\lim_{n \rightarrow \infty} \left[a_{n} \right]^{n} = \left[\lim_{n \rightarrow \infty} a_{n} \right]^{n}$
- $\lim_{n \rightarrow \infty} c = c$
- $\lim_{n \rightarrow \infty} \sqrt[n]{a_{n}} = \sqrt[n]{\lim_{n \rightarrow \infty} a_{n}}$
정리1. 샌드위치 정리(Squeeze Theorem)
충분히 큰 $n \ge n_{0}$에 대해서 $a_{n} \le b_{n} \le c_{n}$이고 $\lim_{n \rightarrow \infty} a_{n} = \lim_{n \rightarrow \infty} c_{n} = L$이면 $\lim_{n \rightarrow \infty} b_{n} = L$이다.
설명

샌드위치 정리를 그림으로 그려보면 위와 같이 그릴 수 있습니다. $b_{n}$은 두 수열 $a_{n}$과 $c_{n}$ 사이에 껴서 점점 한 곳으로 수렴하는 것을 볼 수 있습니다.
정리2.
$\lim_{n \rightarrow \infty} \left|a_{n}\right| = 0$이면 $\lim_{n \rightarrow \infty} a_{n} = 0$이다.
예제1. $\lim_{n \rightarrow \infty} \frac{n}{n + 1}$의 극한을 구하라.
$$\begin{align*} \lim_{n \rightarrow \infty} \frac{n}{n + 1} &= \lim_{n \rightarrow \infty} \frac{1}{1 + \frac{1}{n}} \\ &= \frac{1}{1 + 0} = 1\end{align*}$$
예제2. $\lim_{n \rightarrow \infty} (-1)^{n}$의 극한을 구하라.
$a_{n} = (-1)^{n}$이라고 할 때, $\{a_{n}\} = \{-1, 1, -1, 1, \dots, \}$이기 때문에 수렴하지 않고 발산(진동)한다.
예제3. $\lim_{n \rightarrow \infty} \frac{(-1)^{n}}{n}$의 극한을 구하라.
$a_{n} = \frac{(-1)^{n}}{n}$이라고 할 때, $\lim_{n \rightarrow \infty} \left|a_{n}\right| = \lim_{n \rightarrow \infty} \frac{1}{n} = 0$이다. 정리2에 의해서 $\lim_{n \rightarrow \infty} \frac{(-1)^{n}}{n} = 0$이다.
정리3.
$\lim_{n \rightarrow \infty} a_{n} = L$이고 함수 $f$가 $x = L$에서 연속이면 $\lim_{n \rightarrow \infty} f(a_{n}) = f(L)$이다.
예제4. $\lim_{n \rightarrow \infty} \sin\left(\frac{\pi}{n}\right)$의 극한을 구하라.
$\sin$ 함수는 전 구간에서 연속이기 때문에 정리3에 의해서 $\lim_{n \rightarrow \infty} \sin\left(\frac{\pi}{n}\right) = \sin(0) = 0$이다.
정의1. 증가수열(increasing sequence)과 감소수열(decreasing sequence)
수열 $\{a_{n}\}$이 모든 $n$에 대해서 $a_{n + 1} > a_{n}$이라면 증가수열, $a_{n + 1} < a_{n}$이라면 감소수열이라고 한다.
정의2. 유계 수열(bounded sequence)
수열 $\{a_{n}\}$이 모든 $n$에 대해서 $a_{n} \le M$를 만족하는 $M$이 존재하면 위로 유계(bounded above)이고 $a_{n} \ge m$을 만족하는 $m$이 존재하면 아래로 유계(bounded below)라고 한다. 만약, 수열 $\{a_{n}\}$이 위로 또는 아래로 유계라면 유계 수열(bounded sequence)라고 한다.
정리4. 단조 수열 정리
임의의 유계 단조 수열을 수렴한다.
연습문제1. 주어진 수열이 증감수열인지 또는 둘다 아닌지 판단하라.
(a). $a_{n} = (-2)^{n + 1}$
(b). $a_{n} = \frac{1}{2n + 3}$
(c). $a_{n} = n(-1)^{n}$
(d). $a_{n} = ne^{-n}$
(e). $a_{n} = \frac{n}{n^{2} + 1}$
(f). $a_{n} = n + \frac{1}{n + 1}$
(a). $a_{n} = (-2)^{n + 1}$ Not Monotonic
해당 수열 $a_{n}$은 홀수항에서 양수이고 짝수항에서 음수로 진동하는 수열이기 때문에 증가수열과 감소수열에 모두 속하지 않는다.
(b). $a_{n} = \frac{1}{2n + 3}$ Decreasing Sequence
$$\begin{align*} a_{n + 1} &= \frac{1}{2(n + 1) + 3} \\ &= \frac{1}{2n + 5} \\ &< \frac{1}{2n + 3} = a_{n} \end{align*}$$
모든 $n \in \mathbb{N}$에 대해서 $a_{n} > a_{n + 1}$이기 때문에 감소수열이다.
(c). $a_{n} = n(-1)^{n}$ Not Monotonic
(a)와 유사하게 해당 수열 $a_{n}$은 홀수항에서 음수이게 짝수항에서 양수로 진동하는 수열이기 때문에 증가수열과 감소수열 모두 속하지 않는다.
(d). $a_{n} = ne^{-n}$ Decreasing Sequence
$f(x) = xe^{-x}$라고 하자. 그러면 도함수 $f^{'}(x) = e^{-x} - xe^{-x} = (1 - x)e^{-x}$를 얻을 수 있다. 이때, 모든 $x \ge 1$에 대해서 $e^{-x} > 0$이기 때문에 $f^{'}(x) < 0$이다. 따라서, 함수 $f$는 $[1, \infty)$에서 감소함수이므로 $n \in \mathbb{N}$에 대해서 $a_{n} = f(n) > f(n + 1) = a_{n + 1}$을 만족하여 $a_{n}$은 감소수열이다.
(e). $a_{n} = \frac{n}{n^{2} + 1}$ Decreasing Sequence
$f(x) = \frac{x}{x^{2} + 1}$라고 하자. 그러면 도함수 $f^{'}(x) = \frac{(x^{2} + 1) - 2x^{2}}{(x^{2} + 1)^{2}} = \frac{-x^{2} + 1}{(x^{2} + 1)^{2}}$를 얻을 수 있다. 이때, 모든 $x \ge 1$에 대해서 $(x^{2} + 1)^{2} > 0$이기 때문에 $f^{'}(x) < 0$이다. 따라서, 함수 $f$는 $[1, \infty)$에서 감소함수이므로 $n \in \mathbb{N}$에 대해서 $a_{n} = f(n) > f(n + 1) = a_{n + 1}$을 만족하여 $a_{n}$은 감소수열이다.
(f). $a_{n} = n + \frac{1}{n + 1}$ Increasing Sequence
$f(x) = x + \frac{1}{x + 1}$라고 하자. 그러면 도함수 $f^{'}(x) = 1 - \frac{1}{(x + 1)^{2}}$를 얻을 수 있다. 이때, 모든 $x \ge 1$에 대해서 $f^{'}(x) > 0$이다. 따라서, 함수 $f$는 $[1, \infty)$에서 증가함수이므로 $n \in \mathbb{N}$에 대해서 $a_{n} = f(n) < f(n + 1) = a_{n + 1}$을 만족하여 $a_{n}$은 증가수열이다.
연습문제2. 수열 $a_{n + 1} = \sqrt{2 + a_{n}}$이 초항 $a_{1} = \sqrt{2}$으로 정의되었을 때 수열 $\{ a_{n} \}$은 증가수열이면서 3에 유계임을 증명하고 $a_{n}$의 극한값을 구하여라.
STEP1. 수열 $\{ a_{n} \}$은 증가수열이다.
수열 $\{ a_{n} \}$이 증가수열임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자. 수열 $\{ a_{n} \}$이 증가수열이라는 것은 모든 $n \in \mathbb{N}$에 대해서 $a_{n} < a_{n + 1}$인 것과 동치이다.
1) $n = 1$인 경우 $a_{1} = \sqrt{2}$이고 $a_{2} = \sqrt{2 + \sqrt{2}}$이므로 $a_{1} < a_{2}$이다.
2) $n = k - 1$에 대해서 $a_{k - 1} < a_{k}$이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $a_{k} < a_{k + 1}$임을 증명하면 된다.
$$\begin{align*} a_{k + 1} &= \sqrt{2 + a_{k}} \\ &> \sqrt{2 + a_{k - 1}} = a_{k} \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $a_{n + 1} > a_{n}$이므로 수열 $\{ a_{n} \}$은 증가수열이다.
STEP2. 수열 $\{ a_{n} \}$은 3에 유계이다.
수열 $\{ a_{n} \}$은 3에 유계수열임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자. 수열 $\{ a_{n} \}$이 3에 유계수열이라는 것은 모든 $n \in \mathbb{N}$에 대해서 $a_{n} \le 3$인 것과 동치이다.
1) $n = 1$인 경우 $a_{1} = \sqrt{2} < 3$이다.
2) $n = k - 1$에 대해서 $a_{k - 1} \le 3$이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $a_{k} \le 3$임을 증명하면 된다.
$$\begin{align*} a_{k} = \sqrt{2 + a_{k - 1}} \le \sqrt{2 + 3} = \sqrt{5} < 3 \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $a_{n} \le 3$이므로 수열 $\{ a_{n} \}$은 3에 유계이다.
STEP3. $\lim_{n \rightarrow \infty} a_{n}$
STEP1과 STEP2에 의해 수열 $\{ a_{n} \}$은 증가수열이며 상한선으로 3에 유계되어있음이 증명되었으므로 정리4. 유계단조정리에 의해 수열 $\{ a_{n} \}$의 극한은 수렴한다.
$\lim_{n \rightarrow \infty} a_{n} = L$이라고 할 때 $\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} a_{n}$임 (미적분학 - 수열 연습문제8)을 이용하여 수열 $a_{n + 1} = \sqrt{2 + a_{n}}$의 양변에 $n \rightarrow \infty$으로의 극한을 취해주면 된다.
$$\begin{align*} &\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} \sqrt{2 + a_{n}} \\ &\Rightarrow L = \sqrt{2 + \sqrt{L}} \\ &\Rightarrow (L - 2)(L + 1) = 0 \end{align*}$$
이때, $a_{1} = \sqrt{2}$이고 수열 $\{ a_{n} \}$은 증가수열이므로 $L = 2$이다.
연습문제3. 수열 $a_{n + 1} = 3 - \frac{1}{a_{n}}$이 초항 $a_{1} = 1$으로 정의되었을 때 수열 $\{ a_{n} \}$은 증가수열이면서 3에 유계임을 증명하고 $a_{n}$의 극한값을 구하여라.
STEP1. 수열 $\{ a_{n} \}$은 증가수열이다.
수열 $\{ a_{n} \}$이 증가수열임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자. 수열 $\{ a_{n} \}$이 증가수열이라는 것은 모든 $n \in \mathbb{N}$에 대해서 $a_{n} < a_{n + 1}$인 것과 동치이다.
1) $n = 1$인 경우 $a_{1} = 1$이고 $a_{2} = 3 - 1 = 2$이므로 $a_{1} < a_{2}$이다.
2) $n = k - 1$에 대해서 $a_{k - 1} < a_{k}$이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $a_{k} < a_{k + 1}$임을 증명하면 된다.
$$\begin{align*} a_{k + 1} &= 3 - \frac{1}{a_{k}} \\ &> 3 - \frac{1}{a_{k - 1}} = a_{k} \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $a_{n + 1} > a_{n}$이므로 수열 $\{ a_{n} \}$은 증가수열이다.
STEP2. 수열 $\{ a_{n} \}$은 3에 유계이다.
수열 $\{ a_{n} \}$은 3에 유계수열임을 증명하기 위해 귀류법 (Proof by Contradiction)을 이용하자. 즉, $\{ a_{n} \}$은 3에 유계수열이 아니라고 가정하자. 이는 어떤 $n \in \mathbb{N}$에 대해서 $a_{n} > 3$을 만족하는 것과 동치가 된다. 하지만 $a_{k} = 3 - \frac{1}{a_{k - 1}} > 3 \Rightarrow a_{k - 1} < 0$이 되므로 STEP1에서 얻었던 수열 $\{ a_{n} \}$은 증가수열인 것과 $a_{1} = 1$인 것과 서로 모순된다. 따라서, 귀류법에 의해 수열 $\{ a_{n} \}$은 3에 유계이다.
STEP3. $\lim_{n \rightarrow \infty} a_{n}$
STEP1과 STEP2에 의해 수열 $\{ a_{n} \}$은 증가수열이며 상한선으로 3에 유계되어있음이 증명되었으므로 정리4. 유계단조정리에 의해 수열 $\{ a_{n} \}$의 극한은 수렴한다.
$\lim_{n \rightarrow \infty} a_{n} = L$이라고 할 때 $\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} a_{n}$임 (미적분학 - 수열 연습문제8)을 이용하여 수열 $a_{n + 1} = 3 - \frac{1}{a_{n}}$의 양변에 $n \rightarrow \infty$으로의 극한을 취해주면 된다.
$$\begin{align*} &\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} \left( 3 - \frac{1}{a_{n}} \right) \\ &\Rightarrow L = 3 - \frac{1}{L} \\ &\Rightarrow L^{2} - 3L + 1 = 0 \\ &\Rightarrow L = \frac{3 \pm \sqrt{5}}{2} \end{align*}$$
이때, $a_{1} = 1$이고 수열 $\{ a_{n} \}$은 증가수열이므로 $L = \frac{3 + \sqrt{5}}{2}$이다.
연습문제4. 수열 $a_{n + 1} = \frac{1}{3 - a_{n}}$이 초항 $a_{1} = 2$으로 정의되었을 때 수열 $\{ a_{n} \}$은 감소수열이면서 모든 $n \in \mathbb{N}$에 대해서 $0 < a_{n} \le 2$임을 증명하고 $a_{n}$의 극한값을 구하여라.
STEP1. 모든 $n \in \mathbb{N}$에 대해서 $0 < a_{n} \le 2$이다.
모든 $n \in \mathbb{N}$에 대해서 $0 < a_{n} \le 2$임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자.
1) $n = 1$인 경우 $a_{1} = 2$이므로 $0 < a_{1} = 2 \le 2$를 만족한다.
2) $n = k - 1$에 대해서 $0 < a_{k - 1} \le 2$ 이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $0 < a_{k} \le 2$ 임을 증명하면 된다. 이때, 수학적 귀납법의 가정에 의해 다음과 같이 식을 전개할 수 있다.
$$\begin{align*} &0 < a_{k - 1} \le 2 \\ &\Rightarrow -2 \le -a_{k - 1} < 0 \\ &\Rightarrow 1 \le 3 - a_{k - 1} < 3 \\ &\Rightarrow 0 < \frac{1}{3} \le \frac{1}{3 - a_{k - 1}} = a_{k} < 1 < 2 \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $0 < a_{n} \le 2$이다.
STEP2. 수열 $\{ a_{n} \}$은 감소수열이다.
수열 $\{ a_{n} \}$이 감소수열임을 증명하기 위해 수학적 귀납법 (Mathematical Induction)을 이용하자. 수열 $\{ a_{n} \}$이 감소수열이라는 것은 모든 $n \in \mathbb{N}$에 대해서 $a_{n} > a_{n + 1}$인 것과 동치이다.
1) $n = 1$인 경우 $a_{1} = 2$이고 $a_{2} = \frac{1}{3 - a_{1}} = 1$이므로 $a_{1} > a_{2}$이다.
2) $n = k - 1$에 대해서 $a_{k - 1} > a_{k}$이 성립한다고 가정하자.
3) 마지막으로 $n = k$인 경우에도 $a_{k} > a_{k + 1}$임을 증명하면 된다.
$$\begin{align*} a_{k + 1} &= \frac{1}{3 - a_{k}} \\ &< \frac{1}{3 - a_{k - 1}} = a_{k} \end{align*}$$
1), 2), 3)과 수학적 귀납법에 의해 모든 $n \in \mathbb{N}$에 대해서 $a_{n + 1} < a_{n}$이므로 수열 $\{ a_{n} \}$은 감소수열이다.
STEP3. $\lim_{n \rightarrow \infty} a_{n}$
STEP1과 STEP2에 의해 수열 $\{ a_{n} \}$은 감소수열이며 하한선으로 0에 유계되어있음이 증명되었으므로 정리4. 유계단조정리에 의해 수열 $\{ a_{n} \}$의 극한은 수렴한다.
$\lim_{n \rightarrow \infty} a_{n} = L$이라고 할 때 $\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} a_{n}$임 (미적분학 - 수열 연습문제8)을 이용하여 수열 $a_{n + 1} = \frac{1}{3 - a_{n}}$의 양변에 $n \rightarrow \infty$으로의 극한을 취해주면 된다.
$$\begin{align*} &\lim_{n \rightarrow \infty} a_{n + 1} = \lim_{n \rightarrow \infty} \frac{1}{3 - a_{n}} \\ &\Rightarrow L = \frac{1}{3 - L} \\ &\Rightarrow L(L - 3) = 0 \end{align*}$$
이때, $a_{1} = 2$이고 수열 $\{ a_{n} \}$은 감소수열이므로 $L = 0$이다.
연습문제5. $\lim_{n \rightarrow \infty} a_{n} = 0$이고 수열 $\{ b_{n} \}$이 유계일 때 $\lim_{n \rightarrow \infty} a_{n}b_{n} = 0$임을 증명하라.
Since the sequence $\{ b_{n} \}$ is bounded, there exists $M \in \mathbb{R}$ such that $| b_{n} | \le M$ for all $n \in \mathbb{N}$. Additionally, since $\lim_{n \rightarrow \infty} a_{n} = 0$, for given $\epsilon > 0$, there exists $n \le N$ such that $|a_{n}| < \frac{\epsilon}{M}$.
Consequently, if $n \ge N$, $|a_{n}b_{n} - 0| = |a_{n}b_{n}| = |a_{n}||b_{n}| < \frac{\epsilon}{M} \cdot M = \epsilon$.
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 무한급수의 수렴성 검사 1 (0) | 2022.05.05 |
|---|---|
| 미적분학 - 급수 (0) | 2022.04.28 |
| 미적분학 - 수열 (0) | 2022.04.21 |
| 미적분학 - 극좌표계와 원뿔 단면 곡선 (0) | 2022.04.19 |
| 미적분학 - 원뿔 단면 (0) | 2022.04.14 |
