안녕하세요. 지난 포스팅의 미적분학 - 극좌표계 곡선에서는 극좌표계에서 곡선을 그리는 방법에 대해서 알아보았습니다. 핵심은 특수각들을 차례대로 대입한 뒤 순서대로 곡선을 그리면 되었습니다. 오늘은 극좌표계에서 미분과 적분을 하는 방법에 대해서 알아보도록 하겠습니다.
기본적으로 극좌표계라는 것은 매개변수로 표현된 것이기 때문에 매개변수 미분과 동일하게 할 수 있습니다. 이는 지난 포스팅의 미적분학 - 매개변수와 미적분학을 통해서 알 수 있습니다. 이때, $x = r\cos(\theta)$이고 $y = r\sin(\theta)$이라고 가정해보도록 하겠습니다.
$$\frac{dy}{dx} = \frac{dy / d\theta}{dx / d\theta} = \frac{dr / d\theta \cdot \sin(\theta) + r\cos(\theta)}{dr / d\theta \cdot \cos(\theta) - r\sin(\theta)}$$
예를 들어 $r = 1 + \sin(\theta)$인 곡선이 주어졌을 때 $\theta = \frac{\pi}{3}$에서의 기울기를 구한다고 가정하겠습니다.
$$\begin{align*} \left|\frac{dy}{dx}\right|_{\theta = \frac{\pi}{3}} &= \frac{\cos(\frac{\pi}{3}) \cdot \sin(\frac{\pi}{3}) + (1 + \sin(\frac{\pi}{3}))\cos(\frac{\pi}{3})}{\cos(\frac{\pi}{3}) \cdot \cos(\frac{\pi}{3}) - (1 + \sin(\frac{\pi}{3}))\sin(\frac{\pi}{3})} \\ &= \frac{\frac{1}{2} \cdot \frac{\sqrt{3}}{2} + (1 + \frac{\sqrt{3}}{2})\frac{1}{2}}{\frac{1}{2} \cdot \frac{1}{2} - (1 + \frac{\sqrt{3}}{2})\frac{\sqrt{3}}{2}} \\ &= \frac{\frac{\sqrt{3}}{2} + \frac{1}{2}}{-\frac{1}{2} - \frac{\sqrt{3}}{2}} \\ &= -1\end{align*}$$
다음으로 극좌표계에서 적분을 하는 방법에 대해서 설명드리도록 하겠습니다.
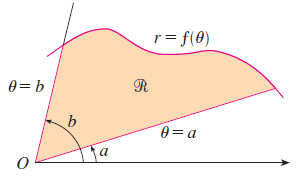
위의 곡선 $r = f(\theta)$를 각도 $\theta = a$부터 $\theta = b$까지 적분하고 싶다고 가정하면 어떻게 할 수 있을까요? 기본적인 적분의 정의를 아시면 쉽게 이해할 수 있기 때문에 지난 포스팅의 미적분학 - 적분의 정의를 보고 와주시길 바랍니다. 항상 적분의 기본은 구간을 작게 등분한 뒤 영역의 넓이를 구하고 합치는 것을 기본으로 합니다. 이는 극좌표계에서도 동일하게 적용됩니다. 다만, 직교좌표계에서는 $x$를 등분했지만, 극좌표계에서는 $\theta$를 등분하는 것의 차이입니다.
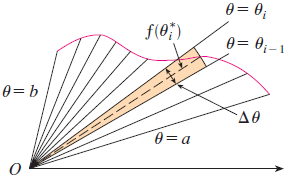
그렇다면, 직교좌표계에서는 등분했을 때, 직사각형을 얻었습니다. 극좌표계에서는 무엇을 얻을 수 있을까요? 위 그림과 같이 작은 부채꼴을 얻을 수 있습니다. $\theta$를 등분했기 때문에 각 부채꼴의 각도는 $\Delta \theta$입니다. 그리고 $\theta_{i}^{*}$를 $i$번째 구간 $[\theta_{i - 1}, \theta_{i}]$에서의 표본점이라고 하겠습니다. 혹시, 지난 포스팅의 미적분학 - 중간점 규칙을 기억하시나요? 적분의 표본점을 정할 때, 구간의 중간점으로 정하면 오차를 줄일 수 있었습니다. 이번에도 동일하게 구간의 중간점 $\theta_{i}^{*} = \frac{\theta_{i} + \theta_{i - 1}}{2}$를 구간의 표본점이라고 하겠습니다.
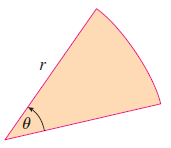
이때, 작은 부채꼴을 확대해서 보면 위와 같은 모양일 겁니다. 부채꼴의 넓이는 다들 아시다싶이 $A = \frac{1}{2}r^{2}\theta$를 통해 얻을 수 있습니다. 따라서, 각 구간의 부채꼴의 넓이는 $A_{i} = \frac{1}{2} r^{2} \Delta \theta = \frac{1}{2} \left[f(\theta_{i}^{*})\right]^{2} \Delta \theta$입니다. 그러므로 $n$개의 구간으로 등분했을 때, 근사된 곡선의 넓이는 아래와 같죠.
$$A \approx \sum_{i = 1}^{n} A_{i} = \sum_{i = 1}^{n} \frac{1}{2} \left[f(\theta_{i}^{*})\right]^{2} \Delta \theta$$
이제, $n \rightarrow \infty$로의 극한을 취해주면 정확한 영역의 넓이를 얻을 수 있습니다.
$$A = \lim_{n \rightarrow \infty} \sum_{i}^{n} \frac{1}{2} \left[f(\theta_{i}^{*})\right]^{2} \Delta \theta = \int_{a}^{b} \frac{1}{2} \left[f(\theta)\right]^{2} d\theta$$
예제1. 극좌표계의 곡선 $r = 1 + \cos(2\theta)$의 1개 잎의 넓이를 구하여라.
STEP1. 극좌표계의 곡선을 그린다.
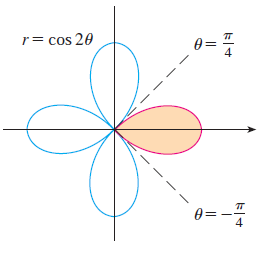
$r = 1 + \cos(2\theta)$에 특수각을 대입하여 위와 같이 그래프를 스케치한다.
STEP2. $\theta$의 시작점과 끝점을 확인하고 적분한다.
$$\begin{align*} A &= \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{1}{2} \left[\cos(2\theta)\right]^{2} \; \theta \\ &= \frac{1}{2} \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \cos^{2}(2\theta) \; d\theta \\ &= \frac{1}{2} \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{1}{2}\left(1 + \cos(4\theta)\right) \; d\theta \\ &= \frac{1}{4} \left[\theta + \frac{1}{4}\sin(4\theta)\right]_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \\ &= \frac{1}{4} \left[\left(\frac{\pi}{4} + \frac{1}{4}\sin(\pi)\right) - \left(\frac{-\pi}{4} + \frac{1}{4}\sin(-\pi)\right)\right] \\ &= \frac{1}{4} \cdot \frac{\pi}{2} \\ &= \frac{\pi}{8}\end{align*}$$
다음으로 알아볼 것은 극좌표계에서 곡선의 길이를 구하는 방법입니다. 이는 지난 포스팅의 미적분학 - 매개변수와 미적분학 2에서 얻은 결과를 활용할 수 있습니다. $x = r\cos(\theta)$이고 $y = r\sin(\theta)$라는 사실만 아시면 됩니다.
$$\begin{align*} L &= \int_{a}^{b} \sqrt{\left(\frac{dx}{d\theta}\right)^{2} + \left(\frac{dy}{d\theta}\right)^{2}} \; d\theta \\ &= \int_{a}^{b} \sqrt{\left(\frac{dr}{d\theta} \cos(\theta) - r\sin(\theta)\right)^{2} + \left(\frac{dr}{d\theta} \sin(\theta) + r\cos(\theta)\right)^{2}} \; d\theta \\ &= \int_{a}^{b} \sqrt{\left[\left(\frac{dr}{d\theta}\right)^{2} \cos^{2}(\theta) - 2r \frac{dr}{d\theta} \cos(\theta) \sin(\theta) + r^{2}\sin^{2}(\theta)\right] + \left[\left(\frac{dr}{d\theta}\right)^{2} \sin(\theta) + 2r \frac{dr}{d\theta} \sin(\theta) \cos(\theta) + r^{2}\cos^{2}(\theta)\right]} \; d\theta \\ &= \int_{a}^{b} \sqrt{\left(\frac{dr}{d\theta}\right)^{2} \left[\sin^{2}(\theta) + \cos^{2}(\theta)\right] + r^{2} \left[\sin^{2}(\theta) + \cos^{2}(\theta)\right]} \; d\theta \\ &= \int_{a}^{b} \sqrt{\left(\frac{dr}{d\theta}\right)^{2} + r^{2}} \; d\theta \end{align*}$$
예제2. 극좌표계의 곡선 $r = 1 + \sin(\theta)$의 곡선의 길이를 구하여라.
STEP1. 극좌표계의 곡선을 그린다.
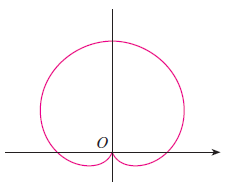
$r = 1 + \sin(\theta)$에 특수각을 대입하여 위와 같이 그래프를 스케치한다.
STEP2. $\theta$의 시작점과 끝점을 확인하고 적분한다.
$$\begin{align*} L &= \int_{0}^{2\pi} \sqrt{r^{2} + \left(\frac{dr}{d\theta}\right)^{2}} \; d\theta \\ &= \int_{0}^{2\pi} \sqrt{\left[1 + \sin(\theta)\right]^{2} + \cos^{2}(\theta)} \; d\theta \\ &= \int_{0}^{2\pi} \sqrt{1 + 2\sin(\theta) + \sin^{2}(\theta) + \cos^{2}(\theta)} \; d\theta \\ &= \int_{0}^{2\pi} \sqrt{2 + 2\sin(\theta)} \; d\theta \\ &= \int_{0}^{2\pi} \frac{\sqrt{2 + 2\sin(\theta)} \cdot \sqrt{2 - 2\sin(\theta)}}{\sqrt{2 - 2\sin(\theta)}} \; d\theta \\ &= \int_{0}^{2\pi} \frac{\sqrt{4 - 4\sin^{2}(\theta)}}{\sqrt{2 - 2\sin(\theta)}} \; d\theta \\ &= \int_{0}^{2\pi} \frac{2\cos(\theta)}{\sqrt{2 - 2\sin(\theta)}} \; d\theta\end{align*}$$
이때, $2 - 2\sin(\theta) = u$라고 하자. 그러면 $0 \le u \le 4$이고 $-2\cos(\theta) d\theta = du \rightarrow d\theta = -\frac{1}{2\cos(\theta)} du$이다. 따라서, 아래와 같이 치환적분 가능하다.
$$\begin{align*} L &= \int_{0}^{2\pi} \frac{2\cos(\theta)}{\sqrt{2 - 2\sin(\theta)}} \; d\theta \\ &= \int_{0}^{4} \frac{2\cos(\theta)}{\sqrt{u}} \; \left(-\frac{1}{2\cos(\theta)} du\right) \\ &= \int_{0}^{4} \frac{1}{\sqrt{u}} \; du \\ &= 2\left[u^{\frac{1}{2}}\right]_{0}^{4} = 4\end{align*}$$
연습문제1. 특정각 $\theta$이 주어졌을 때 극좌표계에서 정의된 곡선에 대한 기울기 (tangent)를 구하시오.
(a). $r = 2\sin(\theta), \theta = \frac{\pi}{6}$
(b). $r = 2 - \sin(\theta), \theta = \frac{\pi}{3}$
(c). $r = \frac{1}{\theta}, \theta = \pi$
(d). $r = \cos(\frac{\theta}{3}), \theta = \pi$
(e). $r = \cos(2\theta), \theta = \frac{\pi}{4}$
(f). $r = 1 + 2\cos(\theta), \theta = \frac{\pi}{3}$
(a). $r = 2\sin(\theta), \theta = \frac{\pi}{6}$
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / d\theta}{dx / d\theta} = \frac{\frac{dr}{d\theta} \sin(\theta) + \cos(\theta)}{\frac{dr}{d\theta} \cos(\theta) - \sin(\theta)} \\ &= \frac{2\cos(\theta)\sin(\theta) + \cos(\theta)}{2\cos(\theta)\cos(\theta) - \sin(\theta)} \\ &= \frac{\sin(2\theta) + \cos(\theta)}{2\cos^{2}(\theta) - \sin(\theta)} \end{align*} - (1)$$
식 (1)에 $\theta = \frac{\pi}{6}$를 대입하여 기울기를 구한다.
$$\begin{align*} \left| \frac{dy}{dx} \right|_{\theta = \frac{\pi}{6}} &= \frac{\sin(\frac{\pi}{3}) + \cos(\frac{\pi}{6})}{2\cos^{2} (\frac{\pi}{6}) - \sin(\frac{\pi}{6})} \\ &= \frac{\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2}}{2 \cdot \frac{3}{4} - \frac{1}{2}} \\ &= \frac{\sqrt{3}}{1} = \sqrt{3} \end{align*}$$
(b). $r = 2 - \sin(\theta), \theta = \frac{\pi}{3}$
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / d\theta}{dx / d\theta} = \frac{\frac{dr}{d\theta} \sin(\theta) + \cos(\theta)}{\frac{dr}{d\theta} \cos(\theta) - \sin(\theta)} \\ &= \frac{(-\cos(\theta))\sin(\theta) + \cos(\theta)}{(-\cos(\theta))\cos(\theta) - \sin(\theta)} \\ &= \frac{-\sin(\theta)\cos(\theta) + \cos(\theta)}{-\cos^{2}(\theta) - \sin(\theta)} \end{align*} - (1)$$
식 (1)에 $\theta = \frac{\pi}{3}$를 대입하여 기울기를 구한다.
$$\begin{align*} \left| \frac{dy}{dx} \right|_{\theta = \frac{\pi}{3}} &= \frac{-\sin(\frac{\pi}{3})\cos(\frac{\pi}{3}) + \cos(\frac{\pi}{3})}{-\cos^{2}(\frac{\pi}{3}) - \sin(\frac{\pi}{3})} \\ &= \frac{-\frac{1}{2} \cdot \frac{\sqrt{3}}{2} + \frac{1}{2}}{-\left( \frac{1}{2} \right)^{2} - \frac{\sqrt{3}}{2}} \\ &= \frac{-\frac{\sqrt{3}}{4} + \frac{1}{2}}{-\frac{1}{4} - \frac{\sqrt{3}}{2}} \\ &= \frac{\sqrt{3} - 2}{1 + 2\sqrt{3}} \end{align*}$$
(c). $r = \frac{1}{\theta}, \theta = \pi$
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / d\theta}{dx / d\theta} = \frac{\frac{dr}{d\theta} \sin(\theta) + \cos(\theta)}{\frac{dr}{d\theta} \cos(\theta) - \sin(\theta)} \\ &= \frac{(-\frac{1}{\theta^{2}})\sin(\theta) + \cos(\theta)}{(-\frac{1}{\theta^{2}})\cos(\theta) - \sin(\theta)} \end{align*} - (1)$$
식 (1)에 $\theta = \pi$를 대입하여 기울기를 구한다.
$$\begin{align*} \left| \frac{dy}{dx} \right|_{\theta = \pi} &= \frac{(-\frac{1}{\pi^{2}})\sin(\pi) + \cos(\pi)}{(-\frac{1}{\pi^{2}})\cos(\pi) - \sin(\pi)} \\ &= \frac{-1}{\frac{1}{\pi^{2}}} = -\pi^{2} \end{align*} $$
(d). $r = \cos(\frac{\theta}{3}), \theta = \pi$
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / d\theta}{dx / d\theta} = \frac{\frac{dr}{d\theta} \sin(\theta) + \cos(\theta)}{\frac{dr}{d\theta} \cos(\theta) - \sin(\theta)} \\ &= \frac{(-\frac{1}{3} \sin(\frac{\theta}{3}))\sin(\theta) + \cos(\theta)}{(-\frac{1}{3} \sin(\frac{\theta}{3}))\cos(\theta) - \sin(\theta)} \end{align*} - (1)$$
식 (1)에 $\theta = \pi$를 대입하여 기울기를 구한다.
$$\begin{align*} \left| \frac{dy}{dx} \right|_{\theta = \pi} &= \frac{(-\frac{1}{3} \sin(\frac{\pi}{3}))\sin(\pi) + \cos(\pi)}{(-\frac{1}{3} \sin(\frac{\pi}{3}))\cos(\pi) - \sin(\pi)} \\ &= \frac{-1}{(-\frac{1}{3} \cdot \frac{\sqrt{3}}{2}) \cdot (-1)} = -2\sqrt{3} \end{align*} $$
(e). $r = \cos(2\theta), \theta = \frac{\pi}{4}$
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / d\theta}{dx / d\theta} = \frac{\frac{dr}{d\theta} \sin(\theta) + \cos(\theta)}{\frac{dr}{d\theta} \cos(\theta) - \sin(\theta)} \\ &= \frac{(-2 \sin(2\theta))\sin(\theta) + \cos(\theta)}{(-2 \sin(2\theta))\cos(\theta) - \sin(\theta)} \end{align*} - (1)$$
식 (1)에 $\theta = \frac{\pi}{4}$를 대입하여 기울기를 구한다.
$$\begin{align*} \left| \frac{dy}{dx} \right|_{\theta = \frac{\pi}{4}} &= \frac{(-2 \sin(2\frac{\pi}{4}))\sin(\frac{\pi}{4}) + \cos(\frac{\pi}{4})}{(-2 \sin(2\frac{\pi}{4}))\cos(\frac{\pi}{4}) - \sin(\frac{\pi}{4})} \\ &= \frac{(-2) \cdot \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}}{(-2) \cdot \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}} \\ &= \frac{-\frac{\sqrt{2}}{2}}{-\frac{3\sqrt{2}}{2}} = \frac{1}{3} \end{align*} $$
(f). $r = 1 + 2\cos(\theta), \theta = \frac{\pi}{3}$
$$\begin{align*} \frac{dy}{dx} &= \frac{dy / d\theta}{dx / d\theta} = \frac{\frac{dr}{d\theta} \sin(\theta) + \cos(\theta)}{\frac{dr}{d\theta} \cos(\theta) - \sin(\theta)} \\ &= \frac{(-2 \sin(\theta))\sin(\theta) + \cos(\theta)}{(-2 \sin(\theta))\cos(\theta) - \sin(\theta)} \end{align*} - (1)$$
식 (1)에 $\theta = \frac{\pi}{3}$를 대입하여 기울기를 구한다.
$$\begin{align*} \left| \frac{dy}{dx} \right|_{\theta = \frac{\pi}{3}} &= \frac{(-2 \sin(\frac{\pi}{3}))\sin(\frac{\pi}{3}) + \cos(\frac{\pi}{3})}{(-2 \sin(\frac{\pi}{3}))\cos(\frac{\pi}{3}) - \sin(\frac{\pi}{3})} \\ &= \frac{(-2 \cdot \frac{\sqrt{3}}{2}) \frac{\sqrt{3}}{2} + \frac{1}{2}}{ (-2 \cdot \frac{\sqrt{3}}{2}) \frac{1}{2} - \frac{\sqrt{3}}{2}} \\ &= \frac{-1}{-\sqrt{3}} = \frac{\sqrt{3}}{3} \end{align*} $$
연습문제2. 극좌표계에서 정의된 곡선의 기울기가 수평 (horizontal) 또는 수직 (vertical)이 되는 각을 구하시오.
(a). $r = 3\cos(\theta)$
(b). $r = 1 - \sin(\theta)$
(c). $r = 1 + \cos(\theta)$
(a). $r = 3\cos(\theta)$
곡선의 기울기가 수평이 되는 경우는 $\frac{dy}{dx} = \frac{dy / d\theta}{dx / d\theta} = 0$인 경우와 같으므로 $\frac{dy}{d\theta} = \frac{dr}
{\theta} \sin(\theta) + r\cos(\theta) = 0$을 만족하는 $\theta$를 찾는다.
$$\begin{align*} \frac{dy}{d\theta} &= \frac{dr}{d\theta} \sin(\theta) + r\cos(\theta) \\ &= (-3 \sin(\theta)) \cdot \sin(\theta) + 3\cos(\theta) \cdot \cos(\theta) \\ &= -3 (\sin^{2} (\theta) - \cos^{2} (\theta)) = -3\cos(2\theta) = 0 \\ \Rightarrow& \cos(2\theta) = 0 \end{align*} - (1)$$
식 (1)을 만족하는 임의의 정수 $n$에 대해서 $2\theta = \frac{(2n + 1) \pi}{2}$이므로 $\theta = \frac{(2n + 1) \pi}{4}$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = \frac{\pi}{4}, \frac{3\pi}{4}, \frac{5\pi}{4}, \frac{7\pi}{4}$이고 이에 대응되는 $r = \frac{3\sqrt{2}}{2}, -\frac{3\sqrt{2}}{2}, -\frac{3\sqrt{2}}{2}, \frac{3\sqrt{2}}{2}$이다. 여기서, $(\frac{3\sqrt{2}}{2}, \frac{\pi}{4}) = (-\frac{3\sqrt{2}}{2}, \frac{5\pi}{4})$ 이고 $(\frac{3\sqrt{3}}{2}, \frac{7\pi}{4}) = (-\frac{3\sqrt{3}}{2}, \frac{3\pi}{4})$ 이므로 유일한 표현을 가지는 극좌표계 점만 정리하면 $(\frac{3\sqrt{2}}{2}, \frac{\pi}{4}), (\frac{3\sqrt{2}}{2}, \frac{7\pi}{4})$이다.
다음으로 곡선의 기울기가 수평이 되는 경우는 $\frac{dy}{dx} = \frac{dy / d\theta}{dx / d\theta} = \infty$인 경우와 같으므로 $\frac{dx}{d\theta} = \frac{dr}{d\theta} \cos(\theta) - r\sin(\theta) = 0$을 만족하는 $\theta$를 찾는다.
$$\begin{align*} \frac{dx}{d\theta} &= \frac{dr}{d\theta} \cos(\theta) - r\sin(\theta) \\ &= (-3 \sin(\theta)) \cdot \cos(\theta) - 3\cos(\theta) \cdot \sin(\theta) \\ &= -6\sin(\theta)\cos(\theta) = -3\sin(2\theta) = 0 \\ \Rightarrow& \sin(2\theta) = 0 \end{align*} - (2)$$
식 (2)을 만족하는 임의의 정수 $n$에 대해서 $2\theta = n \pi$이므로 $\theta = \frac{n \pi}{2}$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = 0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}$이고 이에 대응되는 $r = 3, 0, -3, 0$이다. 여기서, $(3, 0) = (-3, \pi)$ 이고 $(0, \frac{\pi}{2}) = (0, \frac{3\pi}{2})$ 이므로 유일한 표현을 가지는 극좌표계 점만 정리하면 $(3, 0), (0, \frac{\pi}{2})$이다.
마지막으로 $\frac{dy}{dx} = \frac{0}{0}$의 꼴을 가지는 경우는 존재하지 않음을 확인할 수 있다.
1). 기울기가 수평인 점 ($\frac{dy}{d\theta} = 0$): $(\frac{3\sqrt{2}}{2}, \frac{\pi}{4}), (\frac{3\sqrt{2}}{2}, \frac{7\pi}{4})$
2). 기울기가 수직인 점 ($\frac{dx}{d\theta} = 0$): $(3, 0), (0, \frac{\pi}{2})$
(b). $r = 1 - \sin(\theta)$
곡선의 기울기가 수평이 되는 경우는 $\frac{dy}{dx} = \frac{dy / d\theta}{dx / d\theta} = 0$인 경우와 같으므로 $\frac{dy}{d\theta} = \frac{dr}{\theta} \sin(\theta) + r\cos(\theta) = 0$을 만족하는 $\theta$를 찾는다.
$$\begin{align*} \frac{dy}{d\theta} &= \frac{dr}{d\theta} \sin(\theta) + r\cos(\theta) \\ &= (-\cos(\theta)) \cdot \sin(\theta) + (1 - \sin(\theta)) \cdot \cos(\theta) \\ &= -\sin(\theta)\cos(\theta) + \cos(\theta) - \sin(\theta)\cos(\theta) = -2\sin(\theta)\cos(\theta) + \cos(\theta) \\ &= \cos(\theta) (-2\sin(\theta) + 1) = 0 \\ \Rightarrow& \cos(\theta) (2 \sin(\theta) - 1) = 0 \end{align*} - (1)$$
1). $\cos(\theta) = 0$
식 (1)에서 $\cos(\theta) = 0$을 만족하는 임의의 정수 $n$에 대해서 $\theta = \frac{(2n + 1) \pi}{2}$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = \frac{\pi}{2}, \frac{3\pi}{2}$이고 이에 대응되는 $r = 0, 0$이다. 여기서, $(0, \frac{\pi}{2}) = (0, \frac{3\pi}{2})$이므로 유일한
표현을 가지는 극좌표계 점만 정리하면 $(0, \frac{\pi}{2})$이다.
2). $2\sin(\theta) - 1 = 0$
식 (1)에서 $2\sin(\theta) - 1 = 0 \Rightarrow \sin(\theta) = \frac{1}{2}$를 만족하는 임의의 정수 $n$에 대해서 $\theta = \frac{(12n + 1) \pi}{6}$과 $\theta = \frac{(12n + 5)\pi}{6}$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = \frac{\pi}{6}, \frac{5\pi}{6}$이고 이에 대응되는 $r = \frac{1}{2}, \frac{1}{2}$이다. 여기서 얻은 극좌표계점들은 모두 유일한 표현이다.
다음으로 곡선의 기울기가 수평이 되는 경우는 $\frac{dy}{dx} = \frac{dy / d\theta}{dx / d\theta} = \infty$인 경우와 같으므로 $\frac{dx}{d\theta} = \frac{dr}{d\theta} \cos(\theta) - r\sin(\theta) = 0$을 만족하는 $\theta$를 찾는다.
$$\begin{align*} \frac{dx}{d\theta} &= \frac{dr}{d\theta} \cos(\theta) - r\sin(\theta) \\ &= (- \cos(\theta)) \cdot \cos(\theta) - (1 - \sin(\theta)) \cdot \sin(\theta) \\ &= -\cos^{2} (\theta) + \sin^{2} (\theta) - \sin(\theta) \\ &= -(1 - \sin^{2} (\theta)) + \sin^{2} (\theta) - \sin(\theta) \\ &= 2\sin^{2} (\theta) - \sin(\theta) - 1 \\ &= (2\sin(\theta) + 1) (\sin(\theta) - 1) = 0 \\ \Rightarrow& \begin{cases} 2\sin(\theta) + 1 &= 0 \\ \sin(\theta) -1 &= 0 \end{cases} \end{align*} - (2)$$
1). $2\sin(\theta) + 1 = 0$
식 (2)에서 $2\sin(\theta) + 1 = 0 \Rightarrow \sin(\theta) = -\frac{1}{2}$을 만족하는 임의의 정수 $n$에 대해서 $\theta = \frac{(12n - 1) \pi}{2}$과 $\theta = \frac{(12n + 7) \pi}{6}$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = \frac{7\pi}{6}, \frac{11\pi}{6}$이고 이에 대응되는 $r = -\frac{1}{2}$이다. 여기서 얻은 극좌표계점들은 모두 유일한 표현이다.
2). $\sin(\theta) - 1 = 0$
식 (2)에서 $\sin(\theta) - 1 = 0 \Rightarrow \sin(\theta) = 1$를 만족하는 임의의 정수 $n$에 대해서 $\theta = \frac{(4n + 1) \pi}{2}$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = \frac{\pi}{2}이고 이에 대응되는 $r = 1$이다.
마지막으로 $\frac{dy}{dx} = \frac{0}{0}$의 꼴을 가지는 경우는 존재하지 않음을 확인할 수 있다.
1). 기울기가 수평인 점 ($\frac{dy}{d\theta} = 0$): $(0, \frac{\pi}{2}), (\frac{1}{2}, \frac{\pi}{6}), (\frac{1}{2}, \frac{7\pi}{6})$
2). 기울기가 수직인 점 ($\frac{dx}{d\theta} = 0$): $(1, \frac{\pi}{2}), (-\frac{1}{2}, \frac{7\pi}{6}), (-\frac{1}{2}, \frac{11\pi}{6})$
(c). $r = 1 + \cos(\theta)$
곡선의 기울기가 수평이 되는 경우는 $\frac{dy}{dx} = \frac{dy / d\theta}{dx / d\theta} = 0$인 경우와 같으므로 $\frac{dy}{d\theta} = \frac{dr}{\theta} \sin(\theta) + r\cos(\theta) = 0$을 만족하는 $\theta$를 찾는다.
$$\begin{align*} \frac{dy}{d\theta} &= \frac{dr}{d\theta} \sin(\theta) + r\cos(\theta) \\ &= ( -\sin(\theta) ) \cdot \sin(\theta) + ( 1 + \cos(\theta)) \cdot \cos(\theta) \\ &= -\sin^{2} (\theta) + \cos(\theta) + \cos^{2} (\theta) \\ &= - (1 - \cos^{2} (\theta)) + \cos(\theta) + \cos^{2} (\theta) \\ &= 2\cos^{2} (\theta) + \cos(\theta) - 1 \\ &= (2 \cos(\theta) - 1) (\cos(\theta) + 1) = 0 \end{align*} - (1)$$
1). $2\cos(\theta) - 1 = 0$
식 (1)에서 $2\cos(\theta) - 1 = 0 \Rightarrow \cos(\theta) = \frac{1}{2}$을 만족하는 임의의 정수 $n$에 대해서 $\theta = \frac{(6n - 1) \pi}{3}$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = \frac{\pi}{3}, \frac{5\pi}{3}$이고 이에 대응되는 $r = \frac{3}{2}$이다. 따라서, 유일한 표현을 가지는 극좌표계 점만 정리하면 $(\frac{3}{2}, \frac{\pi}{3})$과 $(\frac{3}{2}, \frac{5\pi}{3})$이다.
2). $\cos(\theta) + 1 = 0$
식 (1)에서 $\cos(\theta) + 1 = 0 \Rightarrow \cos(\theta) = -1$를 만족하는 임의의 정수 $n$에 대해서 $\theta =(2n - 1) \pi$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = \pi$이고 이에 대응되는 $r = 0$이다. 따라서, 유일한 표현을 가지는 극좌표계 점만 정리하면 $(0,\pi)$이다.
다음으로 곡선의 기울기가 수평이 되는 경우는 $\frac{dy}{dx} = \frac{dy / d\theta}{dx / d\theta} = \infty$인 경우와 같으므로 $\frac{dx}{d\theta} = \frac{dr}{d\theta} \cos(\theta) - r\sin(\theta) = 0$을 만족하는 $\theta$를 찾는다.
$$\begin{align*} \frac{dx}{d\theta} &= \frac{dr}{d\theta} \cos(\theta) - r\sin(\theta) \\ &= (- \sin(\theta)) \cdot \cos(\theta) - (1 - \sin(\theta)) \cdot \sin(\theta) \\ &= -\sin(\theta)\cos(\theta) - \sin(\theta) - \sin(\theta)\cos(\theta) \\ &= -2\sin(\theta)\cos(\theta) - \sin(\theta) \\ &= -\sin(\theta) (2\cos(\theta) + 1) = 0 \\ \Rightarrow& \begin{cases} \sin(\theta) &= 0 \\ 2\cos(\theta) + 1 &= 0 \end{cases} \end{align*} - (2)$$
1). $\sin(\theta) = 0$
식 (2)에서 $\sin(\theta) = 0$을 만족하는 임의의 정수 $n$에 대해서 $\theta = n\pi$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = 0, \pi$이고 이에 대응되는 $r = 2$와 $r = -1$이다. 따라서, 유일한 표현을 가지는 극좌표계 점만 정리하면 $(2, 0)$과 $(-1, \pi)$이다.
2). $2\cos(\theta) + 1 = 0$
식 (2)에서 $2\cos(\theta) + 1 = 0 \Rightarrow \cos(\theta) = -\frac{1}{2}$를 만족하는 임의의 정수 $n$에 대해서 $\theta = \frac{2(3n - 1) \pi}{3}$이다. 이때, $\theta \in [0, 2\pi)$로 제한하면 $\theta = \frac{4\pi}{3}이고 이에 대응되는 $r = \frac{1}{2}$이다. 따라서, 유일한 표현을 가지는 극좌표계 점만 정리하면 $(\frac{1}{2}, \frac{4\pi}{3})$이다.
마지막으로 $\frac{dy}{dx} = \frac{0}{0}$의 꼴을 가지는 경우는 존재하지 않음을 확인할 수 있다.
1). 기울기가 수평인 점 ($\frac{dy}{d\theta} = 0$): $(\frac{3}{2}, \frac{\pi}{3}), (\frac{3}{2}, \frac{5\pi}{3}), (0, \pi)$
2). 기울기가 수직인 점 ($\frac{dx}{d\theta} = 0$): $(2, 0), (-1, \pi), (\frac{1}{2}, \frac{4\pi}{3})$
연습문제3. 극좌표계에서 다음과 같이 정의된 영역의 넓이를 구하시오.
(a). $r = \theta^{2}, 0 \le \theta \le \frac{4}{\pi}$
(b). $r = e^{\frac{\theta}{2}}, \pi \le \theta \le 2\pi$
(c). $r = \sin(\theta), \frac{\pi}{3} \le \theta \le \frac{2\pi}{3}$
(d). $r = \sqrt{\sin(\theta)}, 0 \le \theta \le \pi$
(a). $r = \theta^{2}, 0 \le \theta \le \frac{4}{\pi}$
해당 곡선은 $f(\theta) = \theta^{2}$이고 단일 곡선으로 구성되어 $0 \le \theta \le \frac{\pi}{4}$에서 다음과 같이 영역의 넓이를 얻을 수 있다.
$$\begin{align*} A &= \int_{0}^{\frac{\pi}{4}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{0}^{\frac{\pi}{4}} \frac{1}{2} \theta^{4} \; d\theta \\ &= \frac{1}{10} \left[ \theta^{5} \right]_{0}^{\frac{\pi}{4}} \\ &= \frac{1}{10} \cdot \left( \frac{\pi}{4} \right)^{5} \end{align*}$$
(b). $r = e^{\frac{\theta}{2}}, \pi \le \theta \le 2\pi$
해당 곡선은 $f(\theta) = e^{\frac{\theta}{2}}$이고 단일 곡선으로 구성되어 $\pi \le \theta \le 2\pi$에서 다음과 같이 영역의 넓이를 얻을 수 있다.
$$\begin{align*} A &= \int_{\pi}^{2\pi} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{\pi}^{2\pi} \frac{1}{2} e^{\theta} \; d\theta \\ &= \frac{1}{2} \left[ e^{\theta} \right]_{\pi}^{2\pi} \\ &= \frac{1}{2} \cdot \left( e^{2\pi} - e^{\pi} \right) \end{align*}$$
(c). $r = \sin(\theta), \frac{\pi}{3} \le \theta \le \frac{2\pi}{3}$
해당 곡선은 $f(\theta) = \sin(\theta)$이고 단일 곡선으로 구성되어 $\frac{\pi}{3} \le \theta \le \frac{2\pi}{3}$에서 다음과 같이 영역의 넓이를 얻을 수 있다.
$$\begin{align*} A &= \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{1}{2} \sin^{2} (\theta) \; d\theta \\ &= \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \frac{1}{2} \cdot \frac{1}{2} (1 - \cos(2\theta)) \\ &= \frac{1}{4} \int_{\frac{\pi}{3}}^{\frac{2\pi}{3}} (1 - \cos(2\theta)) \; d\theta \\ &= \frac{1}{4} \left[ \theta - \frac{1}{2} \sin(2\theta) \right]_{\frac{\pi}{3}}^{\frac{2\pi}{3}} \\ &= \frac{1}{4} \left[ \left( \frac{2\pi}{3} - \frac{1}{2} \sin(\frac{4\pi}{3}) \right) - \left( \frac{\pi}{3} - \frac{1}{2} \sin (\frac{2\pi}{3}) \right) \right] \\ &= \frac{1}{4} \left( \frac{\pi}{3} + \frac{\sqrt{3}}{2} \right) \end{align*}$$
(d). $r = \sqrt{\sin(\theta)}, 0 \le \theta \le \pi$
해당 곡선은 $f(\theta) = \sqrt{\sin(\theta)}$이고 단일 곡선으로 구성되어 $0 \le \theta \le \pi$에서 다음과 같이 영역의 넓이를 얻을 수 있다.
$$\begin{align*} A &= \int_{0}^{\pi} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{0}^{\pi} \frac{1}{2} \sin(\theta) \; d\theta \\ &= \frac{1}{2} \left[ -\cos(\theta) \right]_{0}^{\pi} \\ &= \frac{1}{2} \cdot \left( 1 + 1 \right) = 1 \end{align*}$$
연습문제4. 극좌표계에서 다음과 같이 정의된 영역의 넓이를 구하시오.
(a). $r = 3\cos(\theta)$
(b). $r = 3(1 + \cos(\theta))$
(c). $r^{2} = 4\cos(2\theta)$
(d). $r = 2 - \sin(\theta)$
(e). $r = 2\cos(3\theta)$
(f). $r = 2 + \cos(2\theta)$
(a). $r = 3\cos(\theta)$
해당 곡선으로 둘러쌓인 영역은 반지름이 $\frac{3}{2}$인 원과 같으므로 $A = \frac{3}{2} \cdot \frac{3}{2} \pi = \frac{9}{4}\pi$이다.
(b). $r = 3(1 + \cos(\theta))$
해당 곡선으로 둘러쌓인 영역을 그려보면 $0 \le \theta \le \pi$인 영역과 $\pi \theta \le 2\pi$인 영역이 동일한 것을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= 2\int_{0}^{\pi} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= 2\int_{0}^{\pi} \frac{1}{2} \cdot 9(1 + \cos(\theta))^{2} \; d\theta \\ &= 9 \int_{0}^{\pi} (1 + 2\cos(\theta) + \cos^{2} (\theta)) \; d\theta \\ &= 9\int_{0}^{\pi} (1 + 2\cos(\theta) + \frac{1}{2} (1 + \cos(2\theta))) \; d\theta \\ &= 9 \int_{0}^{\pi} (\frac{3}{2} + 2\cos(\theta) + \frac{1}{2} \cos(2\theta)) \; d\theta \\ &= 9 \left[ \frac{3}{2} \theta + 2\sin(\theta) + \frac{1}{4} \sin(2\theta) \right]_{0}^{\pi} \\ &= 9 \cdot \frac{3}{2}\pi = \frac{27\pi}{2} \end{align*}$$
(c). $r^{2} = 4\cos(2\theta)$
해당 곡선으로 둘러쌓인 영역을 그려보면 $0 \le \theta \le \frac{\pi}{4}$인 영역이 반복되고 $\pi \le \theta 2\pi$는 $0 \le \theta \le \pi$와 동일한 영역임을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= 4 \int_{0}^{\frac{\pi}{4}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= 4 \int_{0}^{\frac{\pi}{4}} \frac{1}{2} \cdot 4\cos(2\theta) \; d\theta \\ &= 8 \int_{0}^{\frac{\pi}{4}} \cos(2\theta) \; d\theta \\ &= 8 \left[ \frac{1}{2} \sin(2\theta) \right]_{0}^{\frac{\pi}{4}} = 4 \end{align*}$$
(d). $r = 2 - \sin(\theta)$
해당 곡선으로 둘러쌓인 영역을 그려보면 $0 \le \theta \le 2\pi$에서 정의된 영역임을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= \int_{0}^{2\pi} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{0}^{2\pi} \frac{1}{2} \cdot (2 - \sin(\theta))^{2} \; d\theta \\ &= \frac{1}{2} \int_{0}^{2\pi} (4 - 4\sin(\theta) + \sin^{2} (\theta)) \; d\theta \\ &= \frac{1}{2} \int_{0}^{2\pi} (4 - 4\sin(\theta) + \frac{1}{2} (1 - \cos(2\theta))) \; d\theta \\ &= \frac{1}{2} \int_{0}^{2\pi} (\frac{9}{2} - 4\sin(\theta) - \frac{1}{2}\cos(2\theta)) \; d\theta \\ &= \frac{1}{2} \left[ \frac{9}{2} \theta + 4\cos(\theta) - \frac{1}{4} \sin(2\theta) \right]_{0}^{2\pi} \\ &= \frac{1}{2} \left[ (\frac{9}{2} \cdot 2\pi + 4\cos(2\pi) - \frac{1}{4} \sin(4\pi)) - (\frac{9}{2} \cdot 0 + 4\cos(0) - \frac{1}{4} \sin(0)) \right] \\ &= \frac{9}{2}\pi \end{align*}$$
(e). $r = 2\cos(3\theta)$
해당 곡선으로 둘러쌓인 영역을 그려보면 $0 \le \theta \le \frac{\pi}{6}$인 영역이 6번 반복는 것을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= 6 \int_{0}^{\frac{\pi}{6}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= 6 \int_{0}^{\frac{\pi}{6}} \frac{1}{2} \cdot 4\cos^{2} (3\theta) \; d\theta \\ &= 12 \int_{0}^{\frac{\pi}{6}} \frac{1}{2}(1 + \cos(6\theta)) \; d\theta \\ &= 6 \int_{0}^{\frac{\pi}{6}} (1 + \cos(6\theta)) \; d\theta \\ &= 6 \left[ \theta + \frac{1}{6}\sin(6\theta) \right]_{0}^{\frac{\pi}{6}} \\ &= 6 \left( \frac{\pi}{6} + \frac{1}{6} \sin(\pi) \right) = \pi \end{align*}$$
(f). $r = 2 + \cos(2\theta)$
해당 곡선으로 둘러쌓인 영역을 그려보면 $0 \le \theta \le \frac{\pi}{2}$인 영역이 4번 반복는 것을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= 4 \int_{0}^{\frac{\pi}{2}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= 4 \int_{0}^{\frac{\pi}{2}} \frac{1}{2} \cdot ( 2 + \cos(2\theta))^{2} \; d\theta \\ &= 2 \int_{0}^{\frac{\pi}{2}} (4 + 4\cos(2\theta) + \cos^{2} (2\theta)) \; d\theta \\ &= 2 \int_{0}^{\frac{\pi}{2}} (4 + 4\cos(2\theta) + \frac{1}{2} (1 + \cos(4\theta))) \; d\theta \\ &= 2 \int_{0}^{\frac{\pi}{2}} (\frac{9}{2} + 4\cos(2\theta) + \frac{1}{2} \cos(4\theta)) \; d\theta \\ &= 2 \left[ \frac{9}{2} \theta + 2 \sin(2\theta) + \frac{1}{8} \sin(4\theta) \right]_{0}^{\frac{\pi}{2}} \\ &= 2 \left( \frac{9}{2} \cdot \frac{\pi}{2} + 2 \sin(\pi) + \frac{1}{8} \sin(2\pi) \right) = \frac{9}{2}\pi \end{align*}$$
연습문제5. 극좌표계에서 다음과 같이 정의된 영역 중 한 주기 (one loop)의 넓이를 구하시오.
(a). $r = \sin(2\theta)$
(b). $r = 4\sin(3\theta)$
(c). $r = 3\cos(5\theta)$
(d). $r = 2\sin(6\theta)$
(a). $r = \sin(2\theta)$
해당 곡선으로 둘러쌓인 영역을 그려보면 한 주기에 해당하는 영역은 $0 \le \theta \le \frac{\pi}{2}$임을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= \int_{0}^{\frac{\pi}{2}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{0}^{\frac{\pi}{2}} \frac{1}{2} \cdot \sin^{2}(2\theta) \; d\theta \\ &= \frac{1}{2} \int_{0}^{\frac{\pi}{2}} \sin^{2} (2\theta) \; d\theta \\ &= \frac{1}{2} \int_{0}^{\frac{\pi}{2}} \frac{1}{2} (1 - \cos(4\theta)) \; d\theta \\ &= \frac{1}{4} \left[ \theta - \frac{1}{4} \sin(4\theta) \right]_{0}^{\frac{\pi}{2}} \\ &= \frac{1}{4} \left( \frac{\pi}{2} - \frac{1}{2} \cdot \sin(2\pi) \right) = \frac{1}{4} \cdot \frac{\pi}{2} = \frac{\pi}{8} \end{align*}$$
(b). $r = 4\sin(3\theta)$
해당 곡선으로 둘러쌓인 영역을 그려보면 한 주기에 해당하는 영역은 $0 \le \theta \le \frac{\pi}{3}$임을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= \int_{0}^{\frac{\pi}{3}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{0}^{\frac{\pi}{3}} \frac{1}{2} \cdot 16\sin^{2}(3\theta) \; d\theta \\ &= 8 \int_{0}^{\frac{\pi}{3}} \sin^{2} (3\theta) \; d\theta \\ &= 8 \int_{0}^{\frac{\pi}{3}} \frac{1}{2} (1 - \cos(6\theta)) \; d\theta \\ &= 4 \left[ \theta - \frac{1}{6} \sin(6\theta) \right]_{0}^{\frac{\pi}{3}} \\ &= 4 \left( \frac{\pi}{3} - \frac{1}{6} \cdot \sin(2\pi) \right) = 4 \cdot \frac{\pi}{3} = \frac{4\pi}{3} \end{align*}$$
(c). $r = 3\cos(5\theta)$
해당 곡선으로 둘러쌓인 영역을 그려보면 한 주기에 해당하는 영역은 $\frac{\pi}{10} \le \theta \le \frac{3\pi}{10}$임을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= \int_{\frac{\pi}{10}}^{\frac{3\pi}{10}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{\frac{\pi}{10}}^{\frac{3\pi}{10}} \frac{1}{2} \cdot 9\cos^{2}(5\theta) \; d\theta \\ &= \frac{9}{2} \int_{\frac{\pi}{10}}^{\frac{3\pi}{10}} \cos^{2} (5\theta) \; d\theta \\ &= \frac{9}{2} \int_{\frac{\pi}{10}}^{\frac{3\pi}{10}} \frac{1}{2} (1 + \cos(10\theta)) \; d\theta \\ &= \frac{9}{4} \left[ \theta + \frac{1}{10} \sin(10\theta) \right]_{\frac{\pi}{10}}^{\frac{3\pi}{10}} \\ &= \frac{9}{4} \left[ \left( \frac{3\pi}{10} + \frac{1}{10} \cdot \sin(3\pi) \right) - \left( \frac{\pi}{10} + \frac{1}{10} \cdot \sin(\pi) \right) \right] = \frac{9}{4} \cdot \frac{\pi}{5} = \frac{9\pi}{20} \end{align*}$$
(d). $r = 2\sin(6\theta)$
해당 곡선으로 둘러쌓인 영역을 그려보면 한 주기에 해당하는 영역은 $0 \le \theta \le \frac{\pi}{6}$임을 알 수 있다. 따라서 다음과 같이 곡선으로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= \int_{0}^{\frac{\pi}{6}} \frac{1}{2} \left[ f(\theta) \right]^{2} \; d\theta \\ &= \int_{0}^{\frac{\pi}{6}} \frac{1}{2} \cdot 4\sin^{2}(6\theta) \; d\theta \\ &= 2 \int_{0}^{\frac{\pi}{6}} \sin^{2} (6\theta) \; d\theta \\ &= 2 \int_{0}^{\frac{\pi}{6}} \frac{1}{2} (1 - \cos(12\theta)) \; d\theta \\ &= \left[ \theta - \frac{1}{12} \sin(12\theta) \right]_{0}^{\frac{\pi}{6}} = \frac{\pi}{6} \end{align*}$$
연습문제6. 아래와 같이 극좌표계에서 정의된 두 개의 곡선이 주어질 때 첫번째 곡선의 내부, 두번째 곡선의 외부에 동시에 포함된 영역의 넓이를 구하여라.
(a). $r = 2\cos(\theta), r = 1$
(b). $r = 1 - \sin(\theta), r = 1$
(c). $r^{2} = 8\cos(2\theta), r = 2$
(d). $r = 2 + \sin(\theta), r = 3\sin(\theta)$
(e). $r = 3\cos(\theta), r = 1 + \cos(\theta)$
(f). $r = 3\sin(\theta), r = 2 - \sin(\theta)$
(a). $r = 2\cos(\theta), r = 1$
두 곡선을 그린 뒤 영역을 확인해보면 $0 \le \theta \le \frac{\pi}{3}$인 영역이 $x$축 대칭으로 나타나는 것을 볼 수 있다. 따라서, 다음과 같이 두 곡선들로 둘러쌓인 영역의 넓이를 구할 수 있다. 여기서 $0 \le \theta \le \frac{\pi}{3}$에서 $2\cos (\theta) \ge 1$임을 고려하여 $f(\theta) = 2\cos(\theta)$ 그리고 $g(\theta) = 1$이라고 하자.
$$\begin{align*} A &= 2 \int_{0}^{\frac{\pi}{3}} \frac{1}{2} \left[ f^{2}(\theta) - g^{2} (\theta) \right] \; d\theta \\ &= \int_{0}^{\frac{\pi}{3}} \left[ 4\cos^{2} (\theta) - 1 \right] \; d\theta \\ &= \int_{0}^{\frac{\pi}{3}} \left[ 4 \cdot \frac{1}{2} \left( 1 + \cos (2\theta) \right) - 1 \right] \; d\theta \\ &= \int_{0}^{\frac{\pi}{3}} (1 + 2\cos(\theta)) \; d\theta \\ &= \left[ \theta + \frac{1}{2} \sin(2\theta) \right]_{0}^{\frac{\pi}{3}} \\ &= \frac{\pi}{3} + \frac{1}{2} \sin(\frac{2\pi}{3}) = \frac{\pi}{3} + \frac{\sqrt{3}}{4} \end{align*}$$
(b). $r = 1 - \sin(\theta), r = 1$
두 곡선을 그린 뒤 영역을 확인해보면 $\pi \le \theta \le \frac{3\pi}{2}$인 영역이 $y$축 대칭으로 나타나는 것을 볼 수 있다. 따라서, 다음과 같이 두 곡선들로 둘러쌓인 영역의 넓이를 구할 수 있다. 여기서 $\pi \le \theta \le \frac{3\pi}{2}$에서 $1 - \sin (\theta) \ge 1$임을 고려하여 $f(\theta) = 1 - \sin(\theta)$ 그리고 $g(\theta) = 1$이라고 하자.
$$\begin{align*} A &= 2 \int_{\pi}^{\frac{3\pi}{2}} \frac{1}{2} \left[ f^{2}(\theta) - g^{2} (\theta) \right] \; d\theta \\ &= \int_{\pi}^{\frac{3\pi}{2}} \left[ (1 - \sin(\theta))^{2} - 1 \right] \; d\theta \\ &= \int_{\pi}^{\frac{3\pi}{2}} \left[ (1 - 2\sin(\theta) + \sin^{2} (\theta)) - 1 \right] \; d\theta \\ &= \int_{\pi}^{\frac{3\pi}{2}} (\frac{1}{2} (1 - \cos(2\theta)) - 2\sin(\theta)) \; d\theta \\ &= \int_{\pi}^{\frac{3\pi}{2}} (\frac{1}{2} - 2\sin(\theta) - \frac{1}{2}\cos(2\theta)) \; d\theta \\ &= \left[ \frac{1}{2} \theta + 2\cos(\theta) - \frac{1}{4} \sin(2\theta) \right]_{\pi}^{\frac{3\pi}{2}} \\ &= ( \frac{1}{2} \cdot \frac{3\pi}{2} + 2\cos(\frac{3\pi}{2} - \frac{1}{4} \sin(3\pi)) ) - (\frac{1}{2} \cdot \pi + 2\cos(\pi) - \frac{1}{4} \sin(2\pi)) \\ &= \frac{3\pi}{4} - \frac{\pi}{2} + 2 = \frac{\pi}{2} + 2 \end{align*}$$
(c). $r^{2} = 8\cos(2\theta), r = 2$
두 곡선을 그린 뒤 영역을 확인해보면 $\pi \le \theta \le \frac{\pi}{6}$인 영역이 $x$축과 $y$축 대칭으로 총 4번 반복되는 것을 볼 수 있다. 따라서, 다음과 같이 두 곡선들로 둘러쌓인 영역의 넓이를 구할 수 있다. 여기서 $0 \le \theta \le \frac{\pi}{6}$에서 $\sqrt{8\cos (2\theta)} \ge 2$임을 고려하여 $f(\theta) = \sqrt{8 \cos(2\theta)}$ 그리고 $g(\theta) = 2$이라고 하자.
$$\begin{align*} A &= 4 \int_{0}^{\frac{\pi}{6}} \frac{1}{2} \left[ f^{2}(\theta) - g^{2} (\theta) \right] \; d\theta \\ &= 2 \int_{0}^{\frac{\pi}{6}} \left[ 8\cos(2\theta) - 4 \right] \; d\theta \\ &= 2 \left[ 4\sin(2\theta) - 4\theta \right]_{0}^{\frac{\pi}{6}} \\ &= 2 \left( 4 \cdot \frac{\sqrt{3}}{2} - 4 \cdot \frac{\pi}{6} \right) = 4 (\sqrt{3} - \frac{\pi}{3}) \end{align*}$$
(d). $r = 2 + \sin(\theta), r = 3\sin(\theta)$
두 곡선을 그린 뒤 영역을 확인해보면 $0 \le \theta \le 2\pi$인 구간에서 곡선 $r = 2 + \sin(\theta)$ 내부에 $r = 3\sin(\theta)$가 존재하는 것을 볼 수 있다. 이때, $r = 3\sin(\theta)$는 반지름이 $\frac{3}{2}$인 원이므로 첫번째 곡선 $r = 2 + \sin(\theta)$의 넓이를 구한 뒤 $\frac{3}{2} \cdot \frac{3}{2} \cdot \pi = \frac{9}{4}\pi$를 빼주면 해당 영역의 넓이를 얻을 수 있다. 여기서, 첫번째 곡선은 $0 \le \theta \le \pi$에서 $y$축 대칭임을 볼 수 있다. 따라서, 다음과 같이 두 곡선들로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= 2 \int_{0}^{\pi} \frac{1}{2} f^{2}(\theta) \; d\theta - \frac{9}{4}\pi \\ &= \int_{0}^{\pi} (2 + \sin(\theta))^{2} \; d\theta - \frac{9}{4}\pi \\ &= \int_{0}^{\pi} (4 + 4\sin(\theta) + \sin^{2} (\theta)) \; d\theta - \frac{9}{4}\pi \\ &= \int_{0}^{\pi} (4 + 4\sin(\theta) + \frac{1}{2} (1 - \cos(2\theta))) \; d\theta - \frac{9}{4} \pi \\ &= \int_{0}^{\pi} (\frac{9}{2} + 4\sin(\theta) - \frac{1}{2}\cos(2\theta)) \; d\theta - \frac{9}{4}\pi \\ &= \left[ \frac{9}{2} \theta - 4 \cos(\theta) - \frac{1}{4} \sin(2\theta) \right]_{0}^{\pi} - \frac{9}{4}\pi \\ &= (\frac{9}{2}\pi + 4) - 4 - \frac{9}{4}\pi = \frac{9}{4}\pi \end{align*}$$
(e). $r = 3\cos(\theta), r = 1 + \cos(\theta)$
두 곡선을 그린 뒤 영역을 확인해보면 $\frac{\pi}{3} \le \theta \le \pi$인 영역이 $y$축 대칭으로 총 2번 반복되는 것을 볼 수 있다. 따라서, 다음과 같이 두 곡선들로 둘러쌓인 영역의 넓이를 구할 수 있다. 여기서 $\frac{\pi}{3} \le \theta \le \pi$에서 $1 + \cos(\theta) \ge 3\cos(\theta)$임을 고려하여 $f(\theta) = 1 + \cos(\theta)$ 그리고 $g(\theta) = 3\cos(\theta)$이라고 하자.
$$\begin{align*} A &= 2 \int_{\frac{\pi}{3}}^{\pi} \frac{1}{2} \left[ f^{2}(\theta) - g^{2} (\theta) \right] \; d\theta \\ &= \int_{\frac{\pi}{3}}^{\pi} \left[ (1 + \cos(\theta))^{2} - 9\cos^{2} (\theta) \right] \; d\theta \\ &= \int_{\frac{\pi}{3}}^{\pi} \left[ (1 + 2\cos(\theta) + \cos^{2} (\theta)) - 9\cos^{2} (\theta) \right] \; d\theta \\ &= \int_{\frac{\pi}{3}}^{\pi} \left( 1 + 2\cos(\theta) - 8\cos^{2} (\theta) \right) \; d\theta \\ &= \int_{\frac{\pi}{3}}^{\pi} \left( 1 + 2\cos(\theta) - 8 \cdot \frac{1}{2} (1 + \cos(2\theta)) \right) \; d\theta \\ &= \int_{\frac{\pi}{3}}^{\pi} \left( -3 + 2\cos(\theta) - 4\cos(2\theta) \right) \; d\theta \\ &= \left[ -3\theta + 2\sin(\theta) - 2\sin(2\theta) \right]_{\frac{\pi}{3}}^{\pi} \\ &= -3\pi - (-\pi + \sqrt{3} + \sqrt{3}) = 2\sqrt{3} - 2\pi \end{align*}$$
(f). $r = 3\sin(\theta), r = 2 - \sin(\theta)$
두 곡선을 그린 뒤 영역을 확인해보면 $\frac{3\pi}{2} \le \theta \le 2\pi$인 영역이 $y$축 대칭으로 총 2번 반복되는 것을 볼 수 있다. 따라서, 다음과 같이 두 곡선들로 둘러쌓인 영역의 넓이를 구할 수 있다. 여기서 $\frac{3\pi}{2} \le \theta \le 2\pi$에서 $2 - \sin(\theta) \ge 3\sin(\theta)$임을 고려하여 $f(\theta) = 2 - \sin(\theta)$ 그리고 $g(\theta) = 3\sin(\theta)$이라고 하자.
$$\begin{align*} A &= 2 \int_{\frac{3\pi}{2}}^{2\pi} \frac{1}{2} \left[ f^{2}(\theta) - g^{2} (\theta) \right] \; d\theta \\ &= \int_{\frac{3\pi}{2}}^{2\pi} \left[ (2 - \sin(\theta))^{2} - 9\sin^{2} (\theta) \right] \; d\theta \\ &= \int_{\frac{3\pi}{2}}^{2\pi} \left[ (4 - 4\sin(\theta) + \sin^{2} (\theta)) - 9\sin^{2} (\theta) \right] \; d\theta \\ &= \int_{\frac{3\pi}{2}}^{2\pi} \left( 4 - 4\sin(\theta) - 8\sin^{2} (\theta) \right) \; d\theta \\ &= \int_{\frac{3\pi}{2}}^{2\pi} \left( 4 - 4\cos(\theta) - 8 \cdot \frac{1}{2} (1 - \cos(2\theta)) \right) \; d\theta \\ &= \int_{\frac{3\pi}{2}}^{2\pi} \left( -4\sin(\theta) + 4\cos(2\theta) \right) \; d\theta \\ &= \left[ 4\cos(\theta) + 2\sin(2\theta) \right]_{\frac{3\pi}{2}}^{2\pi} \\ &= \left( 4\cos(2\pi) + 2\sin(4\pi) \right) - \left( 4\cos(\frac{3\pi}{2}) + 2\sin(3\pi) \right) = 4 \end{align*}$$
연습문제7. 아래와 같이 극좌표계에서 정의된 두 개의 곡선이 주어질 때 두 곡선의 내부에 모두 포함된 영역의 넓이를 구하여라.
(a). $r = \sqrt{3}\cos(\theta), r = \sin(\theta)$
(b). $r = 1 + \cos(\theta), r = 1 - \cos(\theta)$
(c). $r = \sin(2\theta), r = \cos(2\theta)$
(a). $r = \sqrt{3}\cos(\theta), r = \sin(\theta)$
두 곡선을 그린 뒤 영역을 확인해보면 $0 \le \theta \le \frac{\pi}{2}$에서 두 곡선의 내부 영역이 겹치는 것을 볼 수 있다. 그리고 $0 \le \theta \le \frac{\pi}{3}$ 구간에서는 $r = \sin(\theta)$의 내부 영역 $A_{1}$이고 $\frac{\pi}{3} \le \theta \le \frac{\pi}{2}$ 구간에서는 $r = \sqrt{3}\cos(\theta)$의 내부 영역 $A_{2}$ 이다. 따라서, 각 구간에 대한 영역의 넓이를 따로 구해 더하면 전체 넓이를 얻을 수 있다.
1) $A_{1}$ 구하기
$$\begin{align*} A_{1} &= \int_{0}^{\frac{\pi}{3}} \frac{1}{2} \sin^{2} (\theta) \; d\theta \\ &= \frac{1}{2} \int_{0}^{\frac{\pi}{3}} \frac{1}{2} (1 - \cos(2\theta)) \; d\theta \\ &= \frac{1}{4} \left[ \theta - \frac{1}{2} \sin(2\theta) \right]_{0}^{\frac{\pi}{3}} \\ &= \frac{1}{4} \left( \frac{\pi}{3} - \frac{\sqrt{3}}{4} \right) \end{align*}$$
2) $A_{2}$ 구하기
$$\begin{align*} A_{2} &= \int_{\frac{\pi}{3}}^{\frac{\pi}{2}} \frac{1}{2} \cdot 3\cos^{2} (\theta) \; d\theta \\ &= \frac{3}{2} \int_{\frac{\pi}{3}}^{\frac{\pi}{2}} \frac{1}{2} (1 + \cos(2\theta)) \; d\theta \\ &= \frac{3}{4} \left[ \theta + \frac{1}{2} \sin(2\theta) \right]_{\frac{\pi}{3}}^{\frac{\pi}{2}} \\ &= \frac{3}{4} \left( \frac{\pi}{2} - \frac{\pi}{3} - \frac{1}{2} \cdot \frac{\sqrt{3}}{2} \right) = \frac{3}{4} \left( \frac{\pi}{6} - \frac{\sqrt{3}}{4} \right) \end{align*}$$
3) $A = A_{1} + A_{2}$ 구하기
$$\begin{align*} A &= A_{1} + A_{2} \\ &= \frac{1}{4} \left( \frac{\pi}{3} - \frac{\sqrt{3}}{4} \right) + \frac{3}{4} \left( \frac{\pi}{6} - \frac{\sqrt{3}}{4} \right) \\ &= \frac{1}{4} \left( \frac{5\pi}{6} - \sqrt{3} \right) \end{align*}$$
(b). $r = 1 + \cos(\theta), r = 1 - \cos(\theta)$
두 곡선을 그린 뒤 영역을 확인해보면 대칭이기 때문에 겹치는 영역은 $r = 1 + \cos(\theta)$를 기준으로 $\frac{\pi}{2} \le \theta \le \pi$인 영역이 $x$축과 $y축$ 대칭으로 총 4번 반복되는 것을 볼 수 있다. 따라서, 다음과 같이 두 곡선들로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= 4 \int_{\frac{\pi}{2}}^{\pi} \frac{1}{2} f^{2}(\theta) \; d\theta \\ &= 2 \int_{\frac{\pi}{2}}^{\pi} (1 + \cos(\theta))^{2} \; d\theta \\ &= 2 \int_{\frac{\pi}{2}}^{\pi} \left( 1 + 2\cos(\theta) + \cos^{2} (\theta) \right) \; d\theta \\ &= 2 \int_{\frac{\pi}{2}}^{\pi} (1 + 2\cos(\theta) + \frac{1}{2} (1 + \cos(2\theta))) \; d\theta \\ &= 2 \int_{\frac{\pi}{2}}^{\pi} ( \frac{3}{2} + 2\cos(\theta) + \frac{1}{2} \cos(2\theta) ) \; d\theta \\ &= 2 \left[ \frac{3}{2} \theta + 2 \sin(\theta) + \frac{1}{4} \sin(2\theta) \right]_{\frac{\pi}{2}}^{\pi} \\ &= 2 \left( \frac{3}{2}\pi - (\frac{3}{4}\pi + 2) \right) = \frac{3}{2}\pi - 4 \end{align*}$$
(c). $r = \sin(2\theta), r = \cos(2\theta)$
두 곡선을 그린 뒤 영역을 확인해보면 대칭이기 때문에 겹치는 영역은 $r = \cos(2\theta)$를 기준으로 $0 \le \theta \le \frac{\pi}{8}$인 영역이 총 8번 반복되는 것을 볼 수 있다. 따라서, 다음과 같이 두 곡선들로 둘러쌓인 영역의 넓이를 구할 수 있다.
$$\begin{align*} A &= 8 \int_{0}^{\frac{\pi}{8}} \frac{1}{2} f^{2}(\theta) \; d\theta \\ &= 4 \int_{0}^{\frac{\pi}{8}} \cos^{2} (2\theta) \; d\theta \\ &= 4 \int_{0}^{\frac{\pi}{8}} \frac{1}{2} \cdot (1 + \cos(4\theta)) \; d\theta \\ &= 2 \int_{0}^{\frac{\pi}{8}} (1 + \cos(4\theta)) \; d\theta \\ &= 2 \left[ \theta + \frac{1}{4} \sin(4\theta) \right]_{0}^{\frac{\pi}{8}} \\ &= 2 \left( \frac{\pi}{8} + \frac{1}{4} \right) = \frac{\pi}{4} + \frac{1}{2} \end{align*}$$
연습문제8. 아래와 같이 극좌표계에서 정의된 곡선의 길이를 구하여라.
(a).$r = 3\sin(\theta), 0 \le \theta \le \frac{\pi}{3}$
(b).$r = e^{2\theta}, 0 \le \theta \le 2\pi$
(c).$r = \theta^{2}, 0 \le \theta \le 2\pi$
(a).$r = 3\sin(\theta), 0 \le \theta \le \frac{\pi}{3}$
$$\begin{align*} \int_{0}^{\frac{\pi}{3}} \sqrt{\left( \frac{dr}{d\theta} \right)^{2} + r^{2}} \; d\theta \\ &= \int_{0}^{\frac{\pi}{3}} \sqrt{(3\sin(\theta))^{2} + (3\cos(\theta))^{2}} \; d\theta \\ &= \int_{0}^{\frac{\pi}{3}} \sqrt{18} \; d\theta \\ &= 3\sqrt{2} \cdot \frac{\pi}{3} = \sqrt{3} \pi \end{align*}$$
(b).$r = e^{2\theta}, 0 \le \theta \le 2\pi$
$$\begin{align*} \int_{0}^{2\pi} \sqrt{\left( \frac{dr}{d\theta} \right)^{2} + r^{2}} \; d\theta \\ &= \int_{0}^{2\pi} \sqrt{(2e^{2\theta})^{2} + (e^{2\theta})^{2}} \; d\theta \\ &= \int_{0}^{2\pi} \sqrt{4e^{4\theta} + e^{4\theta}} \; d\theta \\ &= \int_{0}^{2\pi} \sqrt{5e^{4\theta}} \; d\theta \\ &= \sqrt{5} \int_{0}^{2\pi} e^{2\theta} \; d\theta \\ &= \sqrt{5} \left[ \frac{1}{2}e^{2\theta} \right]_{0}^{2\pi} \\ &= \frac{\sqrt{5}}{2} \left( e^{4\pi} - 1 \right) \end{align*}$$
(c).$r = \theta^{2}, 0 \le \theta \le 2\pi$
$$\begin{align*} \int_{0}^{2\pi} \sqrt{\left( \frac{dr}{d\theta} \right)^{2} + r^{2}} \; d\theta \\ &= \int_{0}^{2\pi} \sqrt{(2\theta)^{2} + (\theta^{2})^{2}} \; d\theta \\ &= \int_{0}^{2\pi} \sqrt{4\theta^{2} + \theta^{4}} \; d\theta \\ &= \int_{0}^{2\pi} \theta\sqrt{4 + \theta^{2}} \; d\theta \end{align*}$$
이때, $4 + \theta^{2} = u$라고 두면 $2\theta d\theta = du \rightarrow d\theta = \frac{1}{2\theta} du$이고 적분구간은 $[0, 2\pi] \rightarrow [4, 4 + 4\pi^{2}]$이다. 따라서, 다음과 같이 치환적분을 수행할 수 있다.
$$\begin{align*} \int_{0}^{2\pi} \sqrt{\left( \frac{dr}{d\theta} \right)^{2} + r^{2}} \; d\theta = \int_{0}^{2\pi} \theta\sqrt{4 + \theta^{2}} \; d\theta \\ &= \int_{4}^{4 + 4\pi^{2}} \theta \sqrt{u} \cdot \frac{1}{2\theta} \; du \\ &= \frac{1}{2} \int_{4}^{4 + 4\pi^{2}} u^{\frac{1}{2}} \; du \\ &= \frac{1}{2} \cdot \frac{2}{3} \left[ u^{\frac{3}{2}} \right]_{4}^{4 + 4\pi^{2}} \\ &= \frac{1}{3} \left( (4 + 4\pi^{2})^{\frac{3}{2}} - 8 \right) \end{align*}$$
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 극좌표계와 원뿔 단면 곡선 (0) | 2022.04.19 |
|---|---|
| 미적분학 - 원뿔 단면 (0) | 2022.04.14 |
| 미적분학 - 극좌표계 곡선 (0) | 2022.04.09 |
| 미적분학 - 극좌표계 (0) | 2022.04.08 |
| 미적분학 - 매개변수와 미적분학 (0) | 2022.04.06 |
