안녕하세요. 지난 포스팅의 미적분학 - 부정형 극한과 로피탈의 정리에서는 계산하기 어려운 극한에 로피탈의 정리를 적용하는 방법에 대해서 알아보았습니다. 오늘은 미분이 함수의 다양한 정보를 포함하고 있다는 것을 활용하여 복잡한 형태의 함수를 그리는 방법에 대해서 알아보겠습니다.
미적분학 - 목차에서 다양한 주제의 미적분학 관련 포스팅들을 보실 수 있습니다.
기본적으로 함수의 그래프는 아래의 단계를 통해서 그릴 수 있습니다.
1. 함수의 정의역(Domain) 확인 : 함수 $f(x)$가 정의된 영역을 확인합니다.
2. $y$ 절편 확인 : $f(0)$ 값을 확인합니다.
3. 대칭성(Symmetry) 확인 : $f(-x) = f(x)$라면 $f(x)$는 $y$축에 대칭인 우함수(even function), $f(-x) = -f(x)$라면 원점에 대칭인 기함수(odd function)입니다.

이때, $f(x + p) = f(x)$라면 주기가 $p$인 주기함수(periodical function)입니다.

4. 점근성(Asymptotes) 확인
점근성이란 함수가 양/음의 무한대, 또는 특정 값으로 향할 때 어떤 값으로 수렴하는 지를 확인하는 과정입니다. 점근성은 어떤 값으로 향하는 지에 따라서 2가지로 나눌 수 있습니다. 만약, 양/음의 무한대로 향하는 것을 관찰하고자 한다면 이를 수평적 점근성(Horizontal Asymptotes)라고 부르고 특정 값으로 향하는 것을 관찰하고자 한다면 이를 수직적 점근성(Vertical Asymptotes)라고 부릅니다.
5. 함수의 증감 확인 : 미적분학 - 미분과 그래프에서 배웠던 함수의 증감 검사를 통해서 어떤 구간에서 $f^{'}(x)$가 양수인지,음수인지 구별합니다.
6. 함수의 지역 최소값/최대값 확인 : 미적분학 - 미분과 그래프에서 배웠던 지역 최소값/최대값 판별법을 통해서 각 임계점이 지역 최소값인지 최대값인지 확인합니다.
7. 함수의 볼록성 확인 : 미적분학 - 미분과 그래프에서 배웠던 함수의 볼록성 검사를 통해서 어떤 구간에서 $f^{''}(x)$가 양수인지, 음수인지 구별합니다. 이를 통해 특정 구간이 볼록인지, 오목인지 판별가능합니다.
8. 함수 그리기 : 1 - 7까지의 정보를 활용해서 함수를 그립니다.
예제1. 함수 $f(x) = \frac{2x^{2}}{x^{2} - 1}$의 그래프를 그려라.
1. 함수의 정의역 확인
함수 $f(x)$는 유리함수로 분모가 0이 되지 않는 모든 구간이 정의역이다. 따라서 해당 함수의 정의역은 아래와 같다.
$$D(f(x)) = \{x | x^{2} - 1 \neq 0\} = \{x | x \neq \pm 1 \}(-\infty, -1) \cup (-1, 1) \cup (1, \infty)$$
2. $y$ 절편 확인
함수 $f(x)$에서 $x = 0$을 대입하여 그 값을 확인한다.
$$f(0) = \frac{2 \cdot 0^{2}}{0^{2} - 1} = 0$$
3. 대칭성(Symmetry) 확인
함수 $f(x)$에서 $x$ 대신 $-x$를 대입한다.
$$f(-x) = \frac{2\left(-x\right)^{2}}{\left(-x\right)^{2} - 1} = \frac{2x^{2}}{x^{2} - 1} = f(x)$$
$f(-x) = f(x)$ 이므로 함수 $f(x)$는 우함수이다.
4. 점근성(Asymptotes) 확인
기본적으로 수평적 점근성부터 확인한다.
$$\lim_{x \rightarrow \infty} \frac{2x^{2}}{x^{2} - 1} = \lim_{x \rightarrow \infty} \frac{2}{1 - \frac{1}{x^{2}}} = 2$$
$$\lim_{x \rightarrow -\infty} \frac{2x^{2}}{x^{2} - 1} = \lim_{x \rightarrow -\infty} \frac{2}{1 - \frac{1}{x^{2}}} = 2$$
다음으로 함수 $f(x)$가 정의되지 않은 점인 $x = \pm 1$에서 수직적 점근성을 확인한다. 이때, 좌극한과 우극한으로 나누어 계산을 해야 정확하다.
$$\frac{2x^{2}}{x^{2} - 1} = 2 + \frac{-2}{x^{2} - 1}$$
위의 식을 활용하여 $x = \pm 1$에서의 좌극한과 우극한을 계산하면 아래와 같다.
$$\lim_{x \rightarrow 1^{+}} 2 + \frac{-2}{x^{2} - 1} = \infty$$
$$\lim_{x \rightarrow 1^{-}} 2 + \frac{-2}{x^{2} - 1} = -\infty$$
$$\lim_{x \rightarrow (-1)^{+}} 2 + \frac{-2}{x^{2} - 1} = -\infty$$
$$\lim_{x \rightarrow (-1)^{-}} 2 + \frac{-2}{x^{2} - 1} = \infty$$
지금까지의 결과를 그래프로 그리면 아래와 같다.
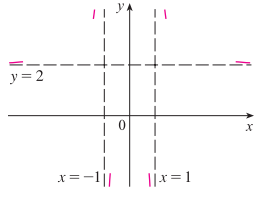
5. 함수의 증감 확인
함수 $f(x)$를 미분하여 어떤 구간에서 증가 및 감소하는 지 확인한다.
$$f^{'}(x) = \frac{4x(x^{2} - 1) - 2x^{2} \cdot 2x}{(x^{2} - 1)^{2}} = \frac{-4x}{(x^{2} - 1)^{2}}$$
$f^{'}(x) = \frac{-4x}{(x^{2} - 1)^{2}} > 0$이려면 $x < 0$이여야하고 $f^{'}(x) = \frac{-4x}{(x^{2} - 1)^{2}} < 0$이려면 $x > 0$이여야한다. 즉, $f(x)$는 양수에서 감소하고 음수에서 증가하는 함수이다.
6. 함수의 지역 최소값/최대값 확인
$f^{'}(x) = 0$이 되는 유일한 값은 $x = 0$이기 때문에 해당 점이 지역 최대 및 최소값을 갖는 지 확인한다. 이때, $x = 0$에서 $f^{'}(x)$의 부호가 양수에서 음수로 변화하기 때문에 해당 점은 지역 최대값이다.
7. 함수의 볼록성 확인
함수 $f(x)$의 이계 도함수 $f^{''}(x)$를 계산하여 어떤 구간에서 볼록 및 오목인지 확인한다.
$$f^{''}(x) = \frac{-4(x^{2} - 1)^{2} + 4x \cdot 2(x^{2} - 1)2x }{(x^{2} - 1)^{4}} = \frac{12x^{2} + 4}{(x^{2} - 1)^{3}}$$
이때, $f^{''}(x) > 0$가 되려면 $x^{2} - 1 > 0$ 이여야하므로 $(-\infty, -1) \cup (1, \infty)$에서 볼록함수이고 $(-1, 1)$에서 오목함수이다.
8. 1 - 7까지의 정보를 종합하여 하나의 그래프로 그린다.
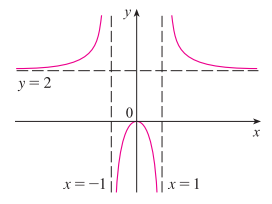
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 적분 정의와 계산 그리고 정적분의 성질 (0) | 2022.01.12 |
|---|---|
| 미적분학 - 영역 문제 (0) | 2021.12.29 |
| 미적분학 - 부정형 극한과 로피탈의 정리 (1) | 2021.12.22 |
| 미적분학 - 미분과 그래프 (0) | 2021.12.20 |
| 미적분학 - 평균값 정리 (Mean Value Theorem; MVT) (0) | 2021.12.18 |
