ThiNet: Pruning CNN Filters for a Tinner Net (IEEE TPAMI2018)

안녕하세요. 오늘은 IEEE TPAMI2018에 게재승인된 모델 경량화 관련 모델인 ThiNet에 대해서 소개하도록 하겠습니다. 

 

ThiNet: Pruning CNN Filters for a Thinner Net

 

 

Background

최근 몇 년간 AlexNet, GoogleNet, ResNet 등의 CNN 모델들이 컴퓨터 비전 분야에서 높은 성능을 달성하며 많은 주목을 받았습니다. 이러한 성공으로 인해 다양한 분야에서 CNN 기반 딥러닝 모델을 활용한 이미지 인식, 객체 탐지 및 의미적 분할 등의 어플리케이션이 크게 증가하게 되었습니다.

 

그러나 높은 성능을 보장하는 CNN 모델들은 일반적으로 많은 연산량과 메모리 자원을 요구하여 모바일이나 웨어러블 디바이스와 같은 제한된 컴퓨팅 리소스를 가진 환경에서는 효율적으로 사용하기 어렵다는 문제가 존재합니다. 이에 따라 MobileNet, ShuffleNet, CondenseNet, GhostNet과 같은 가볍고 효율적인 CNN 모델들이 제안되어 제한된 리소스 환경에서도 활용될 수 있도록 발전해왔습니다.

 

이러한 경량 모델을 개발하는 또 다른 접근법으로 모델 압축(model compression)이 있으며, 특히 pruning 기법은 모델의 구조를 유지하면서도 연산량과 메모리를 효과적으로 줄일 수 있는 방법으로 각광받고 있습니다 (그림 2와 그림 3 참조). 기존의 pruning 방법들은 주로 연결 단위(connection-level)의 가중치를 제거하는 방식으로, 구조적으로 불규칙하고 비정형적인 형태로 압축되어 기존의 딥러닝 라이브러리와 호환되지 않는 문제점이 있었습니다.

 

본 논문에서 제안하는 ThiNet은 필터 단위(filter-level) pruning을 통해 CNN의 구조적 일관성을 유지하면서도 효과적으로 모델의 크기와 연산량을 줄일 수 있는 방법입니다. ThiNet은 다음 레이어의 출력에 기반한 최적화 문제를 통해 중요도가 낮은 필터를 제거함으로써, 기존 방법들보다 더욱 효율적이고 실용적인 CNN 압축을 가능하게 합니다. 본 논문의 기여도를 정리하면 다음과 같습니다. 

 

• 필터 단위(filter-level) Pruning 방법 제안: 기존의 연결 단위(connection-level) Pruning의 문제점인 구조적 불규칙성을 해결하고, CNN 모델의 구조적 일관성을 유지하여 기존의 딥러닝 프레임워크와 높은 호환성을 제공합니다.
• 최적화 기반 필터 중요도 평가: 필터의 중요도를 현재 레이어가 아니라 다음 레이어의 출력에 기반하여 평가하는 최적화 문제를 명확하게 정의하고, 이를 통해 불필요한 필터를 정확하게 선택하여 성능 저하를 최소화합니다.
• Group Convolution with Shuffling (gcos) 방법 제안: 일반적인 그룹 컨볼루션의 단점인 그룹 간 정보 교환 부족 문제를 해결하기 위해 그룹 간의 정보 교환을 효율적으로 가능하게 하는 Group Convolution with Shuffling (gcos) 기법을 제안하여 추가적인 성능 향상을 도모합니다.

Proposed Methods: ThiNet Framework

1) Overall Process

 

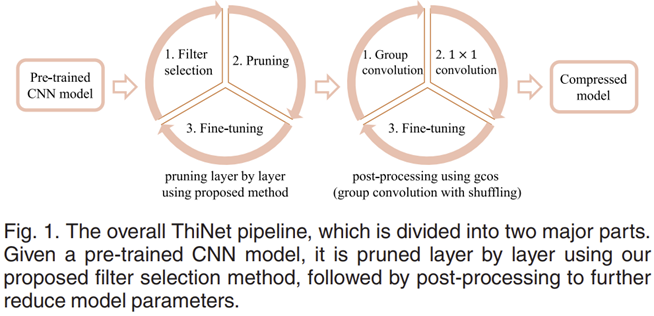
ThiNet은 CNN 모델에서 중요하지 않은 필터를 제거하여, 네트워크를 보다 얇고 효율적으로 만들어주는 필터 수준의 Pruning 기법입니다. ThiNet의 전체적인 프로세스는 다음과 같이 구성됩니다.

 

① 사전 훈련된 CNN 모델에서 중요하지 않은 필터 선별

ThiNet은 이미 훈련된 CNN 모델에서 시작합니다. 여기서 모델 내 각 레이어의 필터들이 실제로 얼마나 중요한지를 평가하여, 중요도가 낮은 필터를 찾아냅니다. 특히 기존의 방법들과는 달리, "현재 레이어의 출력" 이 아닌 "다음 레이어의 출력" 에 기반하여 필터 중요도를 측정합니다. 즉, 특정 필터를 제거했을 때 다음 레이어의 출력이 얼마나 잘 유지되는지를 평가하는 방식입니다.

 

② 중요하지 않은 필터 제거(Pruning)

중요도가 낮다고 평가된 필터들은 네트워크에서 완전히 제거됩니다. 이 과정으로 CNN 모델은 레이어의 개수나 구조는 유지하면서도, 필터의 개수가 줄어들어 더 가볍고 얇아지게 됩니다. 따라서 계산량과 메모리 사용량을 효과적으로 감소시킬 수 있습니다. 

 

③ Group Convolution을 이용한 추가적인 압축 (Post-processing)

ThiNet의 필터 수준의 Pruning은 모델의 구조를 변경하지 않으므로 이후 추가적으로 네트워크를 압축하고 연산을 더 효율적으로 수행하기 위해 그룹 컨볼루션(Group Convolution)을 사용합니다. 하지만 일반적인 그룹 컨볼루션은 서로 다른 그룹 간에 정보를 공유하지 못해 성능이 떨어지는 문제가 있습니다. 이를 해결하기 위해 ThiNet은 1×1 컨볼루션(Point-wise convolution)을 추가적으로 사용하여 서로 다른 그룹 간 정보를 교환하는 기법을 제안하였으며, 이 방법을 "gcos(Group Convolution with Shuffling)" 라고 부릅니다. 이 방법을 통해 그룹 컨볼루션의 효율성을 유지하면서도 성능 감소를 최소화할 수 있습니다.

 

④ 미세조정 (Fine-tuning)

필터 pruning과 압축을 수행하면 모델의 성능이 일부 저하될 수 있으므로, 성능 회복을 위한 fine-tuning 과정이 필요합니다. ThiNet에서는 전체 모델을 한 번에 pruning하는 것이 아니라 각 레이어를 순차적으로 pruning하고, 각 레이어 pruning 후에 빠르게 1에폭에서 2에폭의 fine-tuning을 수행하여 성능을 점진적으로 복구합니다. 마지막 레이어 pruning 이후에는 추가적인 fine-tuning을 통해 모델의 성능을 최대한 복구합니다.

 

2) Part 1: Pruning

2-1) Overview of ThiNet Pruning

 

STEP 1. 필터 선택 (Filter Selection)

ThiNet의 가장 중요한 아이디어는 pruning 대상인 레이어 의 필터 중요도를 평가할 때, 바로 다음 레이어 의 출력을 활용한다는 점입니다. 즉, 레이어 의 입력 채널 중 일부만으로 레이어 의 출력을 잘 근사할 수 있다면, 나머지 채널들은 덜 중요한 것으로 간주하여 안전하게 제거할 수 있다는 원리입니다. 이 과정은 다음과 같이 수행됩니다:

• 레이어 의 입력 채널 중 중요한 채널들을 선별합니다.
• 이 채널들을 이용해 나머지 채널들을 제거해도 레이어 의 출력을 최대한 근사할 수 있도록 최적화 문제를 해결하여 중요도를 평가합니다.

STEP 2. 가지치기 (Pruning)

STEP 1에서 평가된 중요도가 낮은 채널과 이에 대응되는 레이어 의 필터들을 제거하여 모델을 축소합니다. 이 과정에서 레이어 와 레이어 의 입출력 채널 수가 감소하면서 CNN 모델의 크기와 연산량이 줄어들어 더 가벼운 모델이 형성됩니다.

 

STEP 3. 미세조정 (Fine-Tuning)

필터 pruning으로 인해 손상된 모델의 정확도를 회복시키기 위해 미세조정이 필요합니다. 미세조정은 pruning한 레이어마다 수행되며, 각 레이어 pruning 직후 한두 번의 epoch 동안 짧은 미세조정을 진행하여 빠르게 정확도를 회복합니다.

 

STEP 4. 반복 수행 (Iterate)

위 과정(STEP 1~3)을 모든 레이어에 대해 순차적으로 반복합니다. 이를 통해 전체 모델의 연산량과 메모리 사용량을 효율적으로 줄이면서 최종 모델의 성능 손실을 최소화할 수 있습니다.

 

이 부분을 간단하게 수식적으로 정리해보기 위해서 $ ⟨\mathcal{I}_{i}, \mathcal{W}_{i}, * ⟩ $를 $i$번째 계층의 합성곱 연산이라고 정의하겠습니다. 이때, $\mathcal{I}_{i} \in \mathbb{R}^{C \times H \times W}$와 $\mathcal{W}_{i} \in \mathbb{R}^{D \times C \times K \times K}$는 각각 $i$번째 계층의 합성곱 연산을 위한 입력 특징맵과 커널입니다. 따라서, 입력 특징맵 $\mathcal{I}_{i}$는 $C$개의 채널과 함께 $H \times W$의 공간 해상도를 가지며 $\mathcal{W}_{i}$는 $K \times K$ 크기의 커널의 집합으로 출력 특징맵의 채널의 개수를 $D$로 변환하게 됩니다. 

 

이때, ThiNet의 목표는 $\mathcal{W}_{i}$ 내의 중요하지 않은 필터를 없애는 것 입니다. 만약, $\mathcal{W}_{i}$에 포함된 필터하나를 없앤다고 가정하면 이 필터가 생성하는 출력 채널이 없어지게 되겠죠. 따라서, $\mathcal{W}_{i + 1}$이 받는 입력 채널의 개수가 감소하게 될 것이지만 출력 채널의 개수에는 변화가 없습니다. 

 

2-2) Collecting Training Examples

 

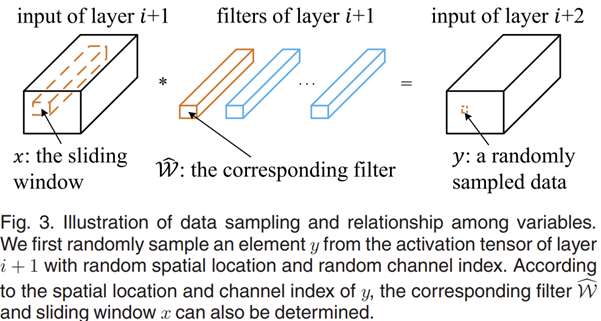
ThiNet에서는 필터의 중요도를 평가하고 어떤 필터가 안전하게 제거될 수 있는지를 결정하기 위해 훈련 데이터를 수집합니다. 이 과정을 해야하는 이유를 먼저 설명해드리도록 하겠습니다. 일단, 표준 합성곱 연산을 다음과 같은 수식으로 전개되죠. 

 

$$y = \sum_{c = 1}^{C} \sum_{k_{1} = 1}^{K} \sum_{k_{2} = 1}^{K} \hat{W}_{c, k_{1}, k_{2}} \times x_{c, k_{1}, k_{2}} + b$$

 

여기서 $\hat{x}_{c, k_{1}, k_{2}} = \sum_{k_{1} = 1}^{K} \sum_{k_{2}}^{K} \hat{W}_{c, k_{1}, k_{2}} \times x_{c, k_{1}, k_{2}}$로 정의하면 위 수식은 다음과 같이 쓸 수 있습니다. 

 

$$\hat{y} = y - b = \sum_{c = 1}^{C} \hat{x}_{c, k_{1}, k_{2}} $$

 

이제, $\hat{x}$와 $\hat{y}$를 랜덤 변수로 간주하며, $\hat{x}$의 각 채널 $\hat{x}_{c}$가 서로 독립적이라는 점을 이용합니다. 만약 특정 채널들의 부분 집합 $S \subseteq \{ 1, 2, \dots, C \}$을 이용하여 $\hat{y} = \sum_{s \in S} \hat{x}_{c}$이 성립한다면 부분 집합 $S$에 포함되지 않은 채널들은 CNN 모델의 결과에 거의 영향을 주지 않으므로 안전하게 제거할 수 있습니다. 하지만, 이 방정식은 두 랜덤 변수 $\hat{x}$와 $\hat{y}$에 대해서 항상 성립하지는 않습니다. 그렇다면 이를 최적화할 수 있도록 하는 과정이 필요하겠죠. 이를 위해서는 $S$를 찾을 수 있는 데이터셋이 필요할 것 입니다. 본 논문에서는 이 섹션에서 이 과정을 설명하고 있습니다. 

 

STEP 1. 순방향 연산 수행

주어진 입력 이미지로부터 CNN 모델을 이용하여 레이어 의 입력과 출력을 순방향 연산(forward run)을 통해 얻습니다.

 

STEP 2. 데이터 샘플링

$(c, k_{1}, k_{2})$에 대해서 $C$ 차원의 벡터 변수 $\hat{\mathbf{x}} = (\hat{x}_{1}, \hat{x}_{2}, \dots, \hat{x}_{C})$와 스칼라 값 $\hat{y}$를 얻습니다. 

 

STEP 3. 추가 데이터 샘플링

이때 저희는 $\hat{x}$와 $\hat{y}$를 랜덤 변수로 간주하였으므로 다양한 입력 이미지, 공간적 위치 및 채널을 달리하여 더 많은 데이터 인스턴스를 수집합니다. 이를 통해 채널 중요도 평가를 위한 풍부한 데이터셋을 구성할 수 있습니다.

 

STEP 4. 데이터셋 구성

최종적으로 수집된 데이터 인스턴스를 이용하여 훈련 행렬 $\mathbf{X} \in \mathbb{R}^{m \times C}$와 타겟 벡터 $\mathbf{y} \in \mathbb{R}^{m \times 1}$을 구성합니다. $m$은 수집된 훈련 샘플의 총 개수를 나타냅니다. 이렇게 수집된 훈련 데이터 $(\mathbf{X}, \mathbf{y})$를 기반으로, 필터의 중요성을 평가하여 제거할 필터와 유지할 필터를 결정하는 데 사용합니다.

 

2-3) Filter Selection and Weight Rescaling

ThiNet에서는 수집된 훈련 데이터를 바탕으로 필터의 중요도를 평가하고, 최적의 필터 집합을 선택하는 과정을 최적화 문제로 접근합니다. 이 과정은 다음과 같은 단계로 이루어집니다:

 

2-3-1) Filter Selection

수집된 훈련 데이터 $(X, y)$를 이용하여 필터 선택 문제를 최적화 문제로 정의합니다. 이 문제는 다음과 같은 수식으로 표현할 수 있습니다:

 

$$\text{argmin}_{S \subseteq \{ 1, 2, \dots, C \}} \sum_{i = 1}^{m} \left( y_{i} - \sum_{j \in S} x_{i, j} \right)^{2} \text{ s.t. } |S| = C \times r$$

 

여기서, $S$는 선택된 필터의 채널 인덱스 집합이고, $r$은 유지할 채널의 수입니다. 하지만 위 문제는 NP-Hard 문제(다항 시간(polynomial-time) 내에 최적해를 찾는 알려진 알고리즘이 없습니다) 이므로 효율적인 근사를 위해 Greedy 전략을 사용하여 문제를 해결합니다. Greedy 전략은 한 번에 하나씩 가장 성능 저하가 적은 채널을 선택하여 최종 필터 집합 를 구성하는 방식입니다. 이 방식을 통해 최적해에 가깝게 효율적으로 채널을 선택할 수 있습니다. 선택된 필터 집합 를 얻은 후, 선택되지 않은 나머지 채널들은 레이어 에서 안전하게 제거할 수 있습니다.

 

2-3-2) Weight Rescaling

채널이 제거되면서 발생하는 출력 재구성 오차를 최소화하기 위해 가중치를 다시 스케일링(weight rescaling)하는 작업이 필요합니다. 이를 다음의 최적화 문제로 정의하여 해결합니다:

 

$$\hat{\mathbf{w}} = \text{argmin}_{\mathbf{w}} \sum_{i = 1}^{m} \left( y_{i} - \hat{x}_{i}\mathbf{w} \right)^{2}$$

 

하지만 위 문제는 선형회귀문제이기 때문에 바로 닫힌 형식으로 답이 $\hat{\mathbf{w}} = \left( \hat{X}^{T}\hat{X} \right)^{-1} \hat{\mathbf{X}}^{T}\mathbf{y}$로 나오게 됩니다. 여기서 $\hat{\mathbf{X}}_{i} = \mathbf{X}_{i, s}$는 선택된 채널들의 데이터 행렬입니다. 이렇게 얻어진 가중치 의 각 원소는 대응되는 필터 채널의 스케일링 인자로 작용하며, 기존의 필터 가중치를 조정하는 데 사용됩니다.

 

$$\mathcal{W}_{i, :, :} = \hat{w}_{i} \mathcal{W}_{i, :, :}$$

 

2-4) Improvement: Integrate Weight Rescaling into Selection

ICCV에 게재되었던 기존 ThiNet 방법에서는 필터 선택(Filter Selection)과 가중치 재조정(Weight Rescaling) 단계가 분리되어 있었습니다. 이러한 접근 방식은 간단하지만, 최적의 필터 선택과 가중치 재조정을 동시에 고려하지 않아 성능이 제한될 수 있습니다. 본 논문에서는 이러한 문제를 해결하기 위해 필터 선택과 가중치 재조정을 하나의 통합된 최적화 문제로 접근하는 방법을 제안합니다. 이 새로운 접근 방법에서는 두 과정을 동시에 고려하여 성능을 더 향상시킬 수 있습니다. 훈련 데이터 $(\mathbf{X}, \mathbf{y})$를 기반으로 필터 선택과 가중치 재조정을 통합하여 아래와 같은 최적화 문제를 정의합니다.

 

$$\text{argmin}_{S \subseteq \{ 1, 2, \dots, C \}} \sum_{i = 1}^{m} \left( y_{i} - \sum_{j \in S} w_{j}X_{i, j} \right)^{2} \text{ s.t. } |S| = C \times r$$

 

이 최적화문제를 통해 필터 선택과 가중치 재조정이 동시에 이루어지며, 이를 통해 보다 정확한 필터 선택과 최적화된 가중치 조정이 가능합니다. 

 

 

3) Post-Processing

 

 

ThiNet의 pruning 과정을 거친 후 추가적으로 모델을 압축하고 성능을 개선하기 위해 후처리(Post-Processing) 과정이 필요합니다. 이 후처리 과정에서 주로 사용하는 방법은 그룹 컨볼루션(Group Convolution)입니다.

 

문제점: 표준 Group Convolution

표준 그룹 컨볼루션은 채널을 여러 개의 그룹으로 나누어 계산합니다. 이때 각 그룹은 독립적으로 작동하며, 서로 간의 정보 교환이 이루어지지 않는 정보 차단(Information Blocking) 문제가 발생합니다. 이로 인해 성능이 제한될 수 있습니다.

 

제안된 방법: Group Convolution with Shuffling (gcos)

ThiNet에서는 이러한 문제를 해결하기 위해 그룹 컨볼루션에 채널 간 정보 교환을 위한 1×1 컨볼루션을 추가한 Group Convolution with Shuffling (gcos) 방식을 제안합니다. 이 방법의 핵심적인 아이디어는 다음과 같습니다:

• 그룹 컨볼루션을 수행한 후, 채널 간 정보를 섞기 위해 1×1 컨볼루션을 적용합니다.
• 1×1 컨볼루션은 그룹 간의 정보 교류를 가능하게 합니다.

Experiment Results

1) Ablation Study

1-1) Different Filter Selection Criteria

 

실험에서는 VGG-16-GAP 모델을 사용하여 두 가지 데이터셋(CUB-200 및 Indoor-67)을 대상으로 여러 필터 선택 방법들 간 성능을 비교하였습니다. 성능은 모델의 연산량(FLOPs)이 감소할 때의 Top-1 정확도로 측정되었습니다.

• 두 데이터셋 모두에서 ThiNet이 다른 모든 방법에 비해 consistently 높은 정확도를 보였습니다.
• 특히 FLOPs가 크게 줄어드는 상황(압축률이 높아질 때)에서도 ThiNet의 성능 감소가 상대적으로 적게 나타났습니다.
• 다른 방법(random, weight sum, APoZ 등)은 압축률이 높아질수록 성능이 급격히 떨어졌지만, ThiNet은 더 완만한 성능 하락을 보였습니다.
• 이는 ThiNet이 효율적인 필터 선택과 가중치 재조정을 통해 모델의 성능을 더욱 효과적으로 유지할 수 있음을 나타냅니다.

즉, 이 실험 결과는 ThiNet의 효과성과 우수성을 잘 보여주며, 다른 전통적인 필터 선택 방식 대비 높은 압축 성능을 제공한다는 결론을 뒷받침합니다.

 

1-2) Different Compression Ratio

 

ResNet-50 모델을 ImageNet 데이터셋에서 ThiNet 방식으로 다양한 압축률을 적용하여 성능을 평가한 결과입니다.

• **원본 모델(Original)**은 Top-1 정확도 75.30%, Top-5 정확도 92.20%이며, 파라미터는 약 25.56M, FLOPs는 약 7.72B입니다.
• **ThiNet으로 pruning한 모델(ThiNet-70, ThiNet-50, ThiNet-30)**의 경우 압축률이 높아질수록 (즉, 숫자가 낮아질수록) 파라미터 수와 FLOPs가 크게 감소하며 추론 속도는 크게 향상됩니다.
• ThiNet-70의 경우 원본 모델 대비 Top-1 정확도가 약 1% 감소했지만, 파라미터 수는 33.7% 감소(25.56M→16.94M), FLOPs는 36.8% 감소(7.72B→4.88B), 추론 속도는 약 13.5% 향상되었습니다(295.12→334.87 images/s).
• 압축률이 높은 ThiNet-30은 정확도 손실이 더 두드러지지만, 파라미터 수는 원본 대비 66.1% 감소(25.56M→8.66M), FLOPs는 약 71.5% 감소(7.72B→2.20B)하며, 추론 속도는 약 34.8%나 향상되었습니다(295.12→397.86 images/s).

결론적으로, ThiNet 방식은 원본 모델에 비해 상당한 연산량 및 파라미터 감소를 달성하면서도, 상대적으로 작은 정확도 손실을 유지하며 추론 속도를 효과적으로 개선할 수 있음을 보여줍니다.

 

2) Image Classification

2-1) Pruning VGG-16 on ImageNet

 

 

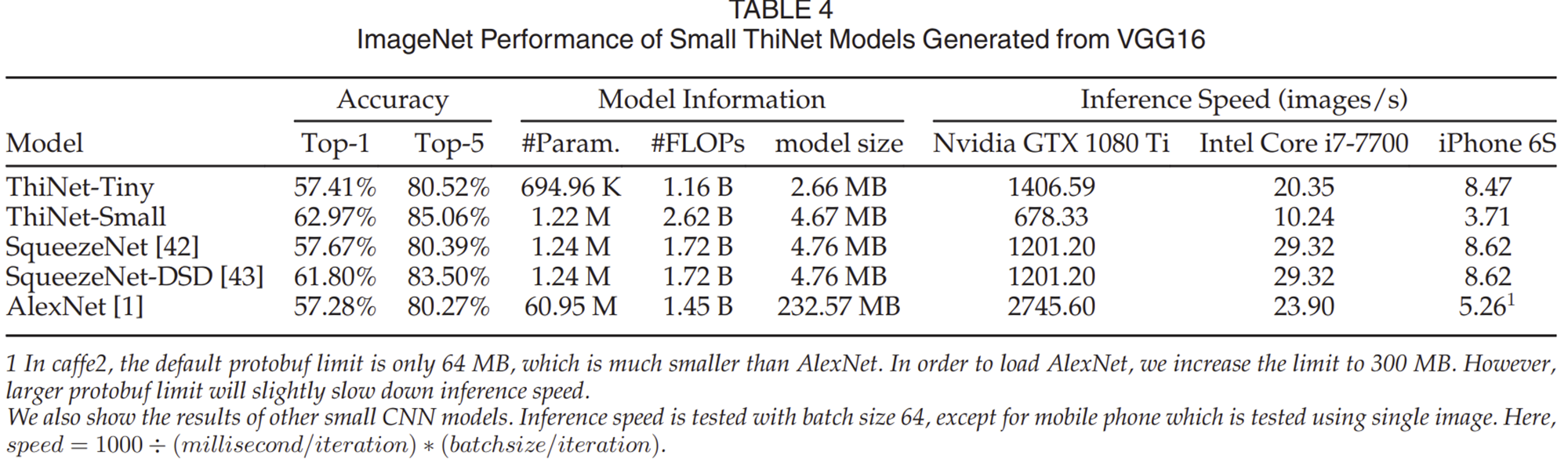
2-2) Pruning VGG-16 on Other Classification Datasets

 

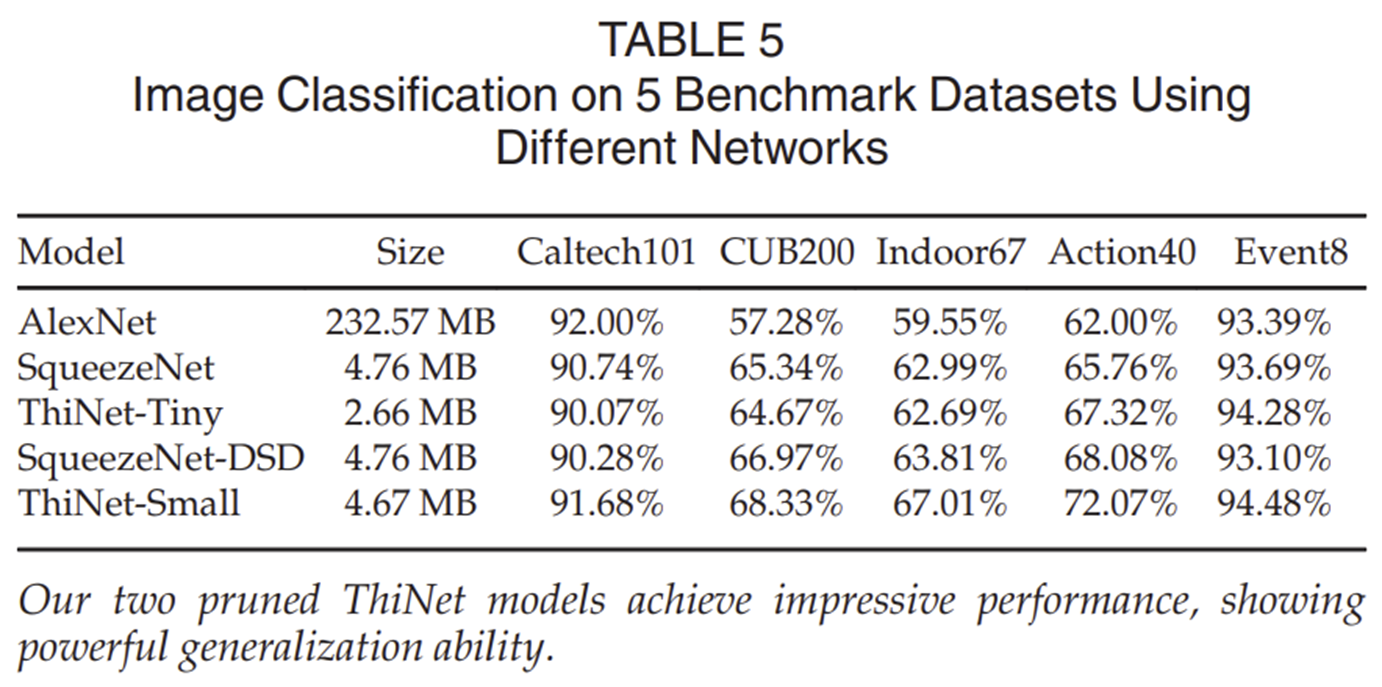
3) Performance Evaluation on Various Visual Tasks

3-1) Image Retrieval 

 

 

3-2) Object Detection

 

3-3) Semantic Segmentation

 

 

3-4) Style Transfer

 

 

Conclusion

본 논문은 CNN 모델 압축을 위한 효율적이고 실용적인 필터 가지치기(pruning) 방법인 ThiNet을 제안하였습니다. ThiNet의 주요 특징은 다음 레이어의 출력을 기반으로 필터 중요도를 평가하여 중요하지 않은 필터를 제거하는 것입니다. 이를 통해 기존 방법들에 비해 더 효과적으로 모델 크기와 연산량을 감소시킬 수 있었습니다.

 

ThiNet은 또한 필터 선택 과정에서 가중치 재조정(weight rescaling)을 통합적으로 수행하여 더 나은 성능을 얻었으며, 추가적으로 Group Convolution with Shuffling (gcos)이라는 방법을 통해 그룹 컨볼루션의 단점인 정보 차단 문제를 극복하였습니다.

 

실험 결과, ThiNet은 기존의 다양한 pruning 방법들과 비교하여 뛰어난 성능과 압축 효율성을 보여주었으며, 높은 압축률에서도 성능 저하를 최소화할 수 있었습니다. 이를 통해 ThiNet은 모바일 및 제한된 컴퓨팅 환경에서도 효율적으로 사용될 수 있는 실질적인 CNN 모델 압축 기술임을 입증하였습니다.